机载搜救相机摆扫运行曲线设计
孙鲁予,刘毓博
(河南水利与环境职业学院,郑州450000)
1 引言
为提高直升机搜救效率,增大搜救相机拍摄视场角,机载搜救相机通常采用摆扫方式获取图像。本文首先依据机载摆扫机构具有的周期短、负载转矩大等特点,提出一种改进型的电机加减速钟形控制曲线。通过Simulink建立步进电机数学模型,将其与常规控制曲线进行仿真与对比。利用TMS320F2812实现了该运动曲线对步进电机的控制,并引入PID控制方法,实现系统闭环控制。
2 摆扫电机模型
2.1 数学模型
根据步进电机电气模型可得两相式混合步进电机的运动方程为

式中:Tm为电机电磁转矩,Jm为电机转轴惯量,JL为负载的等效转动惯量,ω为电机转子的角速度,D为粘滞阻尼系数,TL为负载转矩。
根据距角特性,单相通电时电机的电磁转矩与失调角近似为正弦关系[1]。两相同时通电时,其叠加所成的总电磁转矩依然为正弦,其关系式表示如下:
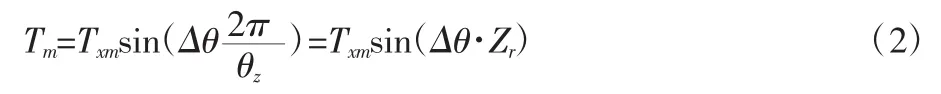
式中:Txm表示最大静转距,Δθ为旋转磁场角位移与转子角位移之差,θz为齿距角,Zr为电机转子齿数。
由转矩与角加速度的关系以及刚度定义可得:

式中:θL表示负载角位移;k表示刚度系数;θM表示电机转轴角位移。
由上式可得两相式混合步进电机运转角度与转矩关系的
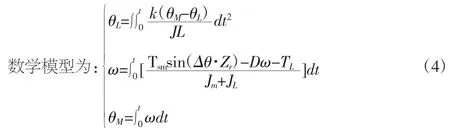
2.2 Simulink仿真模型建立
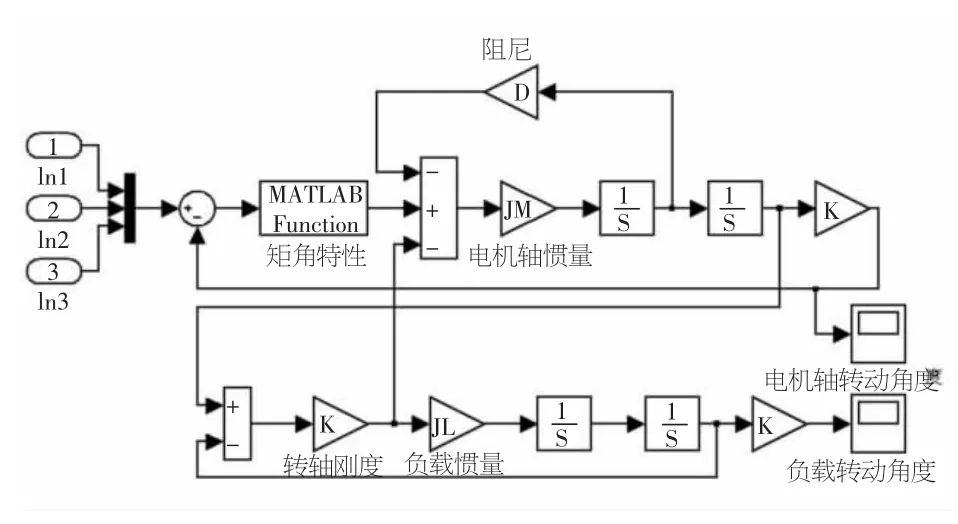
图1 步进电机仿真模型
根据(4)式所得步进电机的数学模型,利用Simulink进行模型的搭建,可得仿真模型如图1所示:图中距角特性为式(2)所示内容,三个输入依次为:电机瞬间加减速控制、恒加速度控制以及钟形加速度控制。
3 电机运行曲线设计与仿真
3.1 运行曲线设计与选取
为满足机载摆扫控制短周期、大惯量背景下电机运转精度和稳定度的要求,需设计合理的电机运行曲线,以避免电机出现丢步和振荡现象。
3.1.1 瞬间加减速控制方式
为证明引入运行曲线的必要性,在仿真中加入未使用运行曲线而使电机瞬间加减速的控制方式作为对比,该方式的电机运行速度由零瞬间加到匀速,并在正程结束时再次瞬间由匀速下降为零,其足以反映未引入运行曲线控制所造成的电机振荡现象。
3.1.2 钟形加速度控制方式
针对上述运行曲线存在的问题和缺点,本文提出一种改进型的运行曲线控制方式,加速阶段的加速度表达式如下:

对其进行积分得到电机转速的数学表达式为:
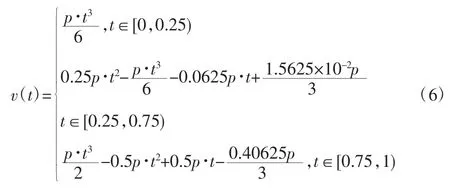
式中p为控制加速度变化的系数,依据实验参数将其定为200。
由于加速度为钟形变化,在加速的开始和完成阶段过渡平滑,可以较好地抑制输入力矩的高频分量,有效地防止谐振激发,降低了电机的振荡现象。仿真结果显示,该方式在加减速所需时间上,该方法总体时间满足摆扫正程时间要求。
3.2 仿真结果对比
机载摆扫实验系统采用的步进电机型号为86BYGH450C。电机参数为:保持转矩,转子齿数50齿,步距角1.8°,转轴惯量Jm=0.4×10-3kg/m2。控制参数设置如表1所示。
4 控制程序设计
4.1 运行曲线加载
考虑到电机控制是实时控制,运行曲线属于以时间为变量的函数,故选用TMS320F2812的CPU定时器0使运行曲线的时间变量产生变化。定时器定时时间设置为1ms,产生中断后,在中断函数中自变量t加1,并根据式(6)计算出实时速度值V,与之前速度值累加后得到角位移值R。将R设置为全局变量,并作为PID控制角位移参考输入变量,实现控制的实时性。
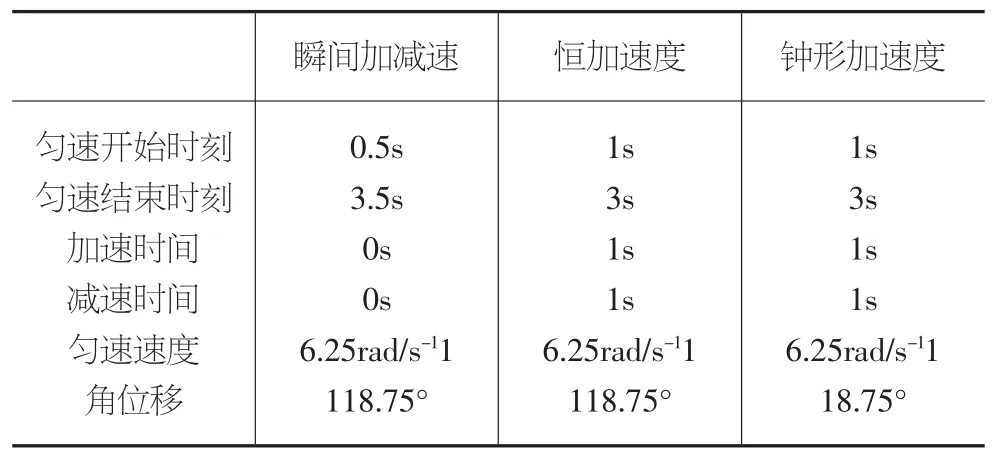
表1 控制参数设置
4.2 PID控制引入
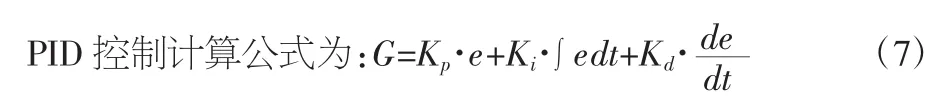
式中:G为输出控制量,e为实际值与控制值之间的误差,Kp为比例项参数,Ki为积分项参数,Kd为微分项参数。
5 结果分析
电机回传角度分析:上位机对电机运行时的角度数据进行获取,在4s时间内采样60次,得到电机角位移与时间实际关系图,并由钟形曲线计算出设计角位移曲线,如图2所示。图中横轴为采样点个数,纵轴为码盘回传数据。从图中可以看出,采用PID闭环控制方式的电机控制系统,其运行曲线与所设计的钟形控制角位移曲线基本相同.
6 结语
本文根据机载搜救相机摆扫时存在的周期短、转动惯量大等特点,设计出一种改进型的步进电机加减速控制曲线。通过步进电机运行原理建立出数学模型,并进行仿真与对比。以上实验说明,该方法适用于机载搜救相机摆扫控制。

