“埋头刷题”不如“抬头寻路”——以一道常见习题为例

罗剑锋

(广东第二师范学院番禺附属中学 511400)

一、一个值得关注的“现象”

正当全国上下火热地研讨“如何提升学生的数学核心素养”的时侯，另一个词“刷题”却也随着互联网的发展成为网络热搜.笔者认为，“埋头刷题”对提高学习成绩能起到立竿见影的效果，但对形成学生终身发展必备品格和关键能力，即数学核心素养成效不大.为此，数学教师就应该在课堂上做好表率，带领学生多“抬头寻路”，从而培养学生分析与思考问题的习惯与能力.

二、两种截然不同的“处理”

日前，听了两节高二年级习题课的“同课异构”，在课堂上，两位教师截然不同的处理方式给笔者留下了深刻的印象.

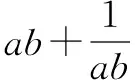
首先是教师甲的课，先从展示典型误解开始：

因为a，b>0，所以ab>0.

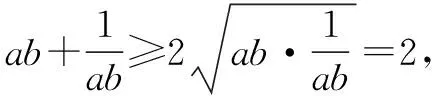
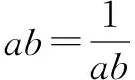
再从典型错误中引出用构造函数的方法解答：

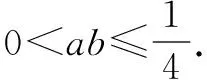
然后是教师乙的课，

问：分析题干，a，b>0，a+b=1是解决本题的前提，看到它，你有什么想法？

问：为什么不直接用基本不等式呢？

生：以前学习过的对勾函数，在(0,1]上递减.也可以用定义法证明它在(0,1]上递减.

问：还有其它不同的解法吗？

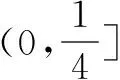
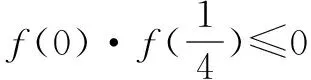
老师及时给予肯定，这是通过“函数与方程的转化思想”进行解题的典型，把方程x2-yx+1=0的解的问题转化成函数f(x)=x2-yx+1与x轴的交点问题，是数与形的完美结合，确实是好办法.

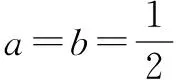
生：我是用“三角换元法”，解法如下：

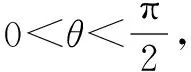
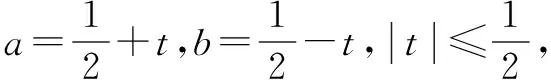
我们在分析问题的时侯，就是要多从不同的角度出发，然后不断地尝试，寻找最佳的解决问题的办法.两位教师讲同一道题时，用了两种截然不同的处理方式

三、三类教学中常问的“问题”

在一线教学中，我们常会碰到这样的学生，平时学习认真，但考试成绩却不理想，究其原因，就是学生的思路没有打开，解决问题的方法比较单一，一旦思路受阻，则选择放弃.所以，教师在课堂上要避免不停地“刷题”，带领学生学会分析与思考，寻找不同的解决问题的办法.笔者认为，结合玻利亚的解题教学理论，在解题教学中，课堂上主要要处理好以下一些问题.

1.启迪学生进行“分析思考”的问题

课堂上，启迪学生进行分析与思考，是新课程体系下教师的主要工作.

为此，教师要在关键点处设问，如乙抛出的第一个问题就是“题干中a，b>0，a+b=1是解决本题的前提，看到它，你有什么想法？”，先让学生弄清题目中已知条件是什么，并通过学生的思考，架起条件与结论之间的桥梁；教师还要在疑难点处设问，在学生思维受阻的地方给出方向与指引，如讲解2012年全国新标卷理科第16题“数列{an}满足an+1+(-1)nan=2n-1，则{an}的前60项和为____”时，学生往往会被(-1)n所吓倒，甚至a1也求不出来，所以此时教师可以设问“单独各项我们是求不出来的，所以求数列{an}的通项公式恐怕不容易，那么连续几项相加减后构成的新数列是否是等差或等比数列呢？”这样一问，学生思维的源泉就能马上打开，课堂上肯定会有很多惊喜.

2.引导学生进行“归纳提升”的问题

只有“分析思考”，没有“归纳提升”，就象一个个活蹦乱跳的孩子，找不到家的感觉.但是，由教师一手包办的“归纳提升”，其效果显然比不上从学生的口中说出来更好一些.如乙在课堂上不停地穿插“你是怎么想到的？”其目的就是想让学生自已对自己的思路进行总结提升，让学生说思路与方法，从而提高对数学的认知.

如上述学生4的回答.当然，一节课要真正做到张弛有度，教师在适当的时侯要自己进行归纳总结，避免学生少走弯路.

3.启发学生进行“拓展思维”的问题

要让学生养成不怕困难、勇于探究的精神和学习习惯，则教师在课堂上启发学生“拓展思维”的问题的设置相当重要，而乙常常追问“还有别的解法吗？”的做法显得相当宝贵.这样，课堂上就能充分地把学生的思维给暴露出来，一节课下来，学生就会明白他的想法好不好？好在哪？不好在哪？

数学课堂上的“一题多解”与“一题多变”就是启发学生进行“拓展思维”很好的做法，它们是中国数学教育教学方式的“瑰宝”，是摆脱师生“埋头刷题”的重要举措.

笔者认为，无论是课上还是课下，“埋头刷题”或许能做到“熟能生巧”，但要想真正内化为学生自身的能力和素养，课上教师应该先带领学生“抬头寻路”.