如何用高等数学知识解初等数学题

关 键

(黑龙江省大庆四中 163000)

数学知识是相通的，许多高等数学中的解题方法可直接用来求解初等数学题，使我们能快速地确定解题思路，进而能够找出更简捷的解题方法.因此作为高中的数学教师在进行教学时，可以教会学生一些高等数学的解题方法，以帮助他们能够用多种方法解决初等数学问题，同时还可以激发学生学习数学的积极性，提高他们解决实际问题的能力.

一、高等数学与初等数学之间的联系

初等数学是高等数学的基础，高等数学是由初等数学发展而来的.因此只有先学习和掌握了初等数学知识才能够学会和运用高等数学知识.同理，学习高等数学知识有助于加深对初等数学知识的理解，进一步提高学生解决问题的能力.如在研究函数的增减性以及求极值和最值等一些特性时，具有较大的局限性.如果用高等数学知识中的极限、级数和导数就可以很好地解决函数的特性问题.有些题可以选择用高等数学知识和初等数学知识同时解决，通过对比，提高学生对这两种方法的理解和认知水平，同时还可以激发学生的学习兴趣.有些问题在初等数学中没有得到充分的解决，但是应用高等数学知识就很容易解答.如函数的递增性问题.

二、高等数学知识解决初等数学题的应用

1.用高等数学知识解决初等数学中不等式的问题

如可以利用柯西不等式或者用导数的性质证明不等式等.运用高等数学知识中的导数方法证明不等式，把需要证明的一元不等式通过构造成函数的方式转化 成了关于x的函数，然后再通过求F(x)的最值的方法达到证明不等式的目的.进而打破了利用初等数学解不等式的局限性，也最终能够使不等式这类问题得到充分的解决.

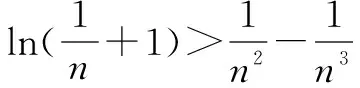
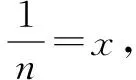
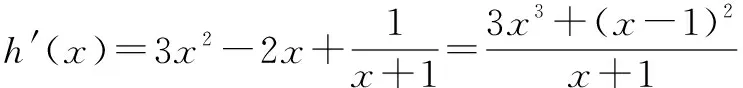
通过解题可知，当F(x)在[a,b]上单调递增，则aF(a)．如果f(a)=φ(a)，要证明当x>a时，f(x)>φ(x)，那么，只要令F(x)=f(x)-φ(x)，就可以利用F(x)的单调增性来推导．也就是说，在F(x)可导的前提下，只要证明F′(x)>0即可．

2.高等数学中离散数学在初等数学问题中的应用

离散数学的内容包括数理逻辑、数论、图论、集合论以及代数结构等知识.其中利用数理逻辑的方法解决初等数学问题，具有较强的概括性和推理便捷性，便于分析.

如对于若P则Q类的证明，可以顺着P、Q的成立条件来进行分析，当P满足时Q则满足，意识P为Q的先导条件.可以假设P已经成立时，推导出Q是否成立，命题即可得到证明.具体证明实例如下.

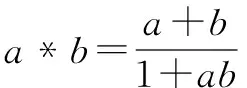
3.常微分方程的建模技术应用

方程在实际问题的解决中占有非常重要的地位，它是解决问题的一种重要的方法.笛卡儿曾经设想过把任何问题转化为数学问题然后再把任何数学问题转化为代数问题，再指导代数问题归结为解方程的万能方法.虽然笛卡儿的设想没有成功，但是它仍然是个伟大的思想.常微分方程建模技术的形成，让方程的思想发挥越来越重要的作用.如有一个空水池，如果单独灌水需24个小时灌满，单独排水需48小时.如果同时灌水和排水，用多少小时可将空水池灌满？可以设水池的容积为V，水池灌满所需的时间为t建立方程，结果需要48小时灌满水.但是在实际中，可以用灌水为衡量，排水是随水池水位下降流量而不断减少的.而简单通过建立微分方程是无法灌满水的，通过实验或者观察而求解的做法是行不通的.通过建立和处理数学模型，把数学理论知识运用于实际的问题中，问题就迎刃而解了.

用高等数学中的理论和方法对初等数学的相关问题进行分析，可以很好地拓宽学生的解题思路；把高等数学中的一些内容融合到初等数学中，还可促进学生更好地学习初等数学知识，使学生的思维更加灵活.