突然扩散水跃方程的显式解

宁利中，渠亚伟，宁碧波，王新宏，田伟利，刘 爽

(1. 西安理工大学西北旱区生态水利工程国家重点实验室培育基地，陕西西安 710048; 2. 嘉兴学院建筑工程学院,浙江嘉兴 314001； 3. 上海大学建筑系,上海 200444)

高水头泄水建筑物的下泄水流具有水头高、流速大、水流集中的特点，故下泄水流的动能很大。为了使下泄水流与下游河道水流正常平顺衔接，必须在泄水建筑物下游尽可能短的范围内或所规定区域内集中消减下泄水流的动能，以确保建筑物与河道的安全。对于具体的水流条件、地形地质条件、泄水建筑物的形式与布置等，必须采取不同的消能方式。水跃或者底流消能作为基本的消能方式之一，已在工程中广泛应用。关于水跃消能的研究也已获得很大进展[1-6]。

水平渠底等宽矩形断面渠道中的水跃是水跃的最简单形式，它具有共轭水深比的显式解。但是，限于地形条件，消能段经常布置成扩散式水跃消能，因此，需研究水平渠底渐扩明渠段中的水跃[7-12]及水平突然扩散段(简称水平突扩段)的水跃[7,13-19]。水平突扩水跃的共轭水深是底流消能工水力设计的重要参数。本文将研究突扩水跃共轭水深方程及其水力特性。首先研究回流平均水深，并通过试验资料确定回流平均水深关系中的系数α。然后，应用动量守恒原理推导突扩水跃方程，并给出突扩水跃方程的显式解。

1 理论分析

1.1 突扩水跃方程

图1是水平渠底突扩水跃的流动示意图。h1,h2为跃前、跃后断面水深，h3为回流区平均水深，b，B为上游、下游渠槽宽度。

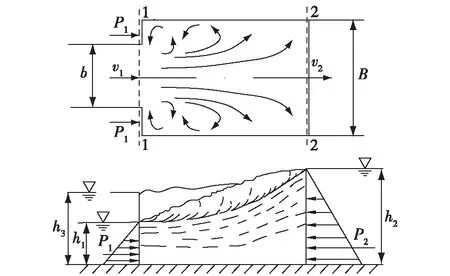
图1 突扩式水跃示意Fig.1 Hydraulic jump in abruptly expanding channel

对图1所示的流动运用动量原理建立共轭水深关系式前，作出如下假定：①跃前与跃后断面上的水流为渐变流,动水压力服从静水压力分布；②跃前与跃后断面上的动量修正系数相等，数值为1.0；③忽略明渠(槽)底壁面的摩擦阻力。

在流动方向对图1的跃前与跃后两断面应用动量原理，有

(1)

式中：Q为流量；γ为水重度；g为重力加速度；v1为跃前断面平均流速,v2为跃后断面平均流速；α01,α02分别为跃前断面和跃后断面的动量修正系数；Pi为流动方向作用的力。

根据连续性原理，有：Q=v1h1b=v2h2B

(2)

根据假定(1)，跃前断面的动水总压力为：

(3)

(4)

始端扩散区壁面压强与回流平均水深有关，它是确定始端扩散区壁面压强的重要参数。回流水深沿始端扩散区壁面变化。为了方便计算，通常选用平均回流水深计算水跃始端扩散断面上的动水总压力，即

(5)

根据假定(2)，有：α01=α02=1.0。

(6)

将式(2)～(6)代入式(1)，得

(7)

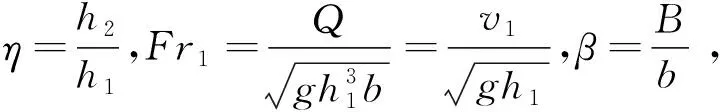
(8)

式(8)即为突扩水跃的共轭水深方程。

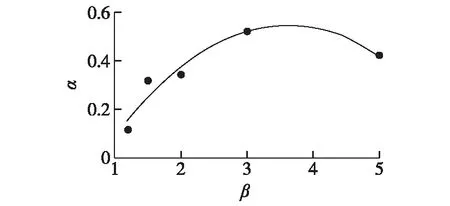
图2 系数α随着突扩比β的变化Fig.2 Variation of coefficient α with abrupt expansion ratio β

1.2 回流平均水深

由于回流水深沿始端扩散区壁面是变化的，本文认为回流平均水深h3是跃前、跃后水深h1,h2的函数，同时又受突扩比β影响。假定

(9)

式中：系数α可由试验确定。根据文献[7]和[9]关于回流水深的试验资料，发现系数α是突扩比β的函数，如图2所示，其关系式可表示为

α=-0.066 9β2+0.484 6β-0.329

(10)

显然，系数α小于0.5，在β=3.0左右存在极值。 回流水深系数由5个试验数据确定，每个试验数据取相同扩散比情况下10多个试验数据的平均值。

1.3 水跃方程显式解

将式(9)代入式(8)，得

(11)

整理式(11)，得

(12)

式(12)即为假设条件下突扩水跃的共轭水深方程。对于方程(12)，参照文献[20]处理一元三次方程的方法，则共轭水深方程的解为

(13a)

(13b)

2 水跃方程显式解的验证

水跃方程显式解与文献[13,18]试验结果的比较见表1。

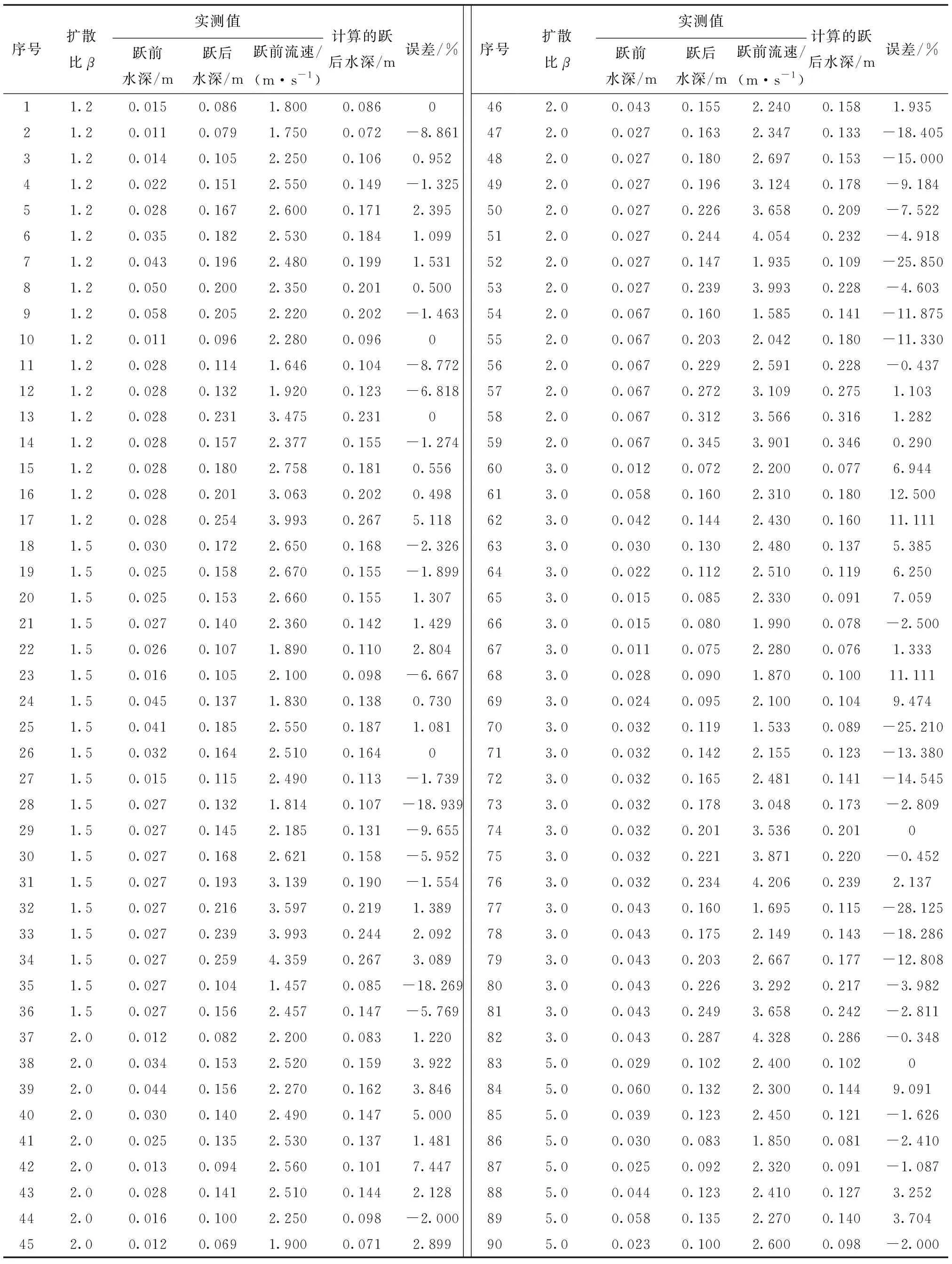
表1 显式解与试验资料[13,18]的比较Tab.1 Comparison between explicit solutions and experimental data

不同突扩比情况下水跃方程显式解与文献[13,18]试验结果的平均误差和最大误差分析见表2。计算共轭水深比与试验共轭水深比的比较见图3。可以看出:①水跃方程显式解与试验的平均误差为5.481%，最大误差为28.125%，最大误差发生在β=3.0的情况。②不同突扩比情况下水跃方程显式解与文献[13,18]试验结果的比较说明，最大平均误差发生在β=3.0的情况下,最小平均误差发生在β=1.2的情况。最大误差和不同突扩比情况下，最大平均误差都发生在β=3.0的情况，说明这种情况流动最复杂，个别试验点的试验情况和理论假定偏离较大。另外，也不排除个别试验点在试验观测时存在较大误差。③在90组试验数据中，水跃方程显式解与试验的误差小于5%的有57组，占试验资料的63.3%。误差大于20%的仅有3组，占试验资料的3.3%。这说明，水跃方程显式解是可靠的，具有较高精度，可用于计算实际工程问题。

表2不同突扩比时显式解与试验结果的误差

Tab.2 Errors between explicit solution at different abrupt expansion ratios and experimental data

突扩比β=1.2β=1.5β=2.0β=3.0β=5.0平均误差/%2.4214.5636.2478.6332.896最大误差/%8.86118.93925.85028.1259.091

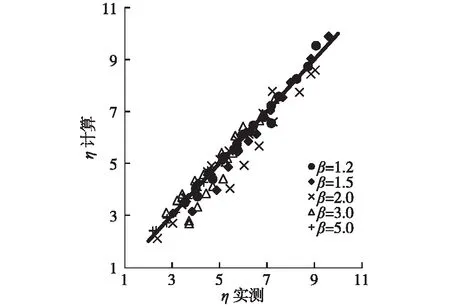
图3 共轭水深比计算结果与试验结果比较Fig.3 Comparison between calculated results and experimental results of conjugate depth

3 结 语