土工布包裹对粗粒料三轴试验的影响研究
夏家南,梁 彬,汤书明,朱俊高
(1. 河海大学岩土力学与堤坝工程教育部重点实验室,江苏南京 210098; 2. 中设设计集团股份有限公司,江苏南京 210005; 3. 上海市隧道工程轨道交通设计研究院,上海 200032)
近年来粗粒料被广泛应用于土石坝、铁路和公路路基、桥梁墩台、软基处理和高填方等工程,尤其在土石坝中粗粒料的应用越来越广泛。据统计,自20世纪50年代后期以来,世界各国采用堆石料的高土石坝占比达70%~80%,并且还有继续发展的趋势[1-3]。粗粒料作为主要的填筑材料用量巨大,它的力学性质对工程安全和正常使用起到关键性作用,因此,针对粗粒料的研究越来越多[4]。为了得到粗粒料的力学性质需对其进行常规三轴试验,但是粗粒料的试样表面凹凸不平且布满了棱边和尖角,即使是特制的厚橡皮膜也会在中等压力下被刺穿而发生漏水,所以必须采取一定的措施消除这种不利影响。国内外学者对橡皮膜的刺穿问题有了一定的研究,并在试验中采取了相应的措施。例如,孔德志等[5]在试验中采用了两层厚度分别为0.8和2.0 mm的橡皮膜,并在两层橡皮膜之间加设了3 mm厚的橡皮板;张启岳[6]在试验中采用了特制的粘附有正六角块的内衬膜,以及外套防漏膜;孔祥臣[7]在试验中采用两层1.5 mm厚的橡皮膜,并且在里层衬上由5块约4 mm厚的活动胶板;司洪洋[8]提出在内膜和外膜之间填砂的组合结构;国外的学者采用了在膜与试样间放入小块薄铜片、硅橡胶等方法[9-10]。
本文采用在试样表面包裹土工布的方法来保护橡皮膜,但是土工布的包裹对试样的径向变形有约束作用,从而影响到试样的变形和强度。因此,进行了包裹土工布和未包裹土工布的常规三轴固结排水对比试验,分析研究土工布对试样强度和变形的影响程度。
表1坝壳粗粒料原级配及缩尺级配
Tab.1 Original and scale gradation of coarse-grained materials of dam shell
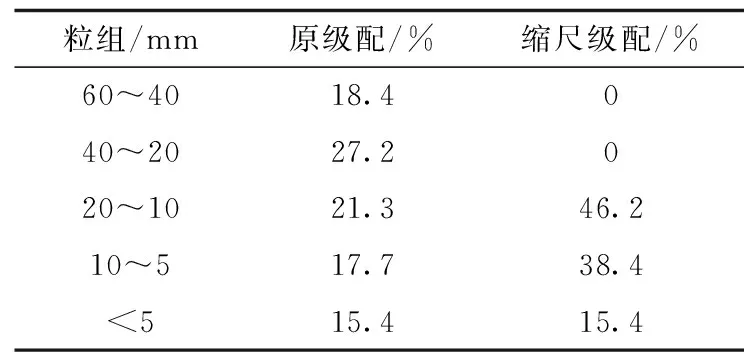
粒组/mm原级配/%缩尺级配/%60~4018.4040~2027.2020~1021.346.210~517.738.4<515.415.4
1 试验方案
1.1 试验土样
试验采用云南糯扎渡土石坝的坝壳粗粒料,该材料为正长石花岗岩,岩性新鲜和微风化,粒度均匀,棱角尖锐,其原级配如表1所示。由于试样直径为101 mm,《土工试验规程》[11]规定最大允许粒径为20 mm,因此必须对原级配进行缩尺。试验采用等量替代法进行缩尺,缩尺后级配如表1所示。
1.2 土工布特性
试验采用无纺土工布。无纺土工布是土工合成材料的一种,其物理力学特性如表2所示。

表2 土工布物理力学特性Tab.2 Physical and mechanical properties of geotextiles
1.3 试验方案
试样直径为101 mm,高度为200 mm。制样时土层分5层击实,控制干密度ρd为1.90 g/cm3。进行包裹土工布的中型三轴试验时,制样过程中还需要将土工布(宽21 cm,长35~37 cm)卷成圈后放入对开膜内,并使其平整贴于对开膜内壁。
制样完成后对试样进行饱和固结。将压力室灌满水并密封,向压力室施加20 kPa的围压,使厚橡皮膜与标准橡皮膜及土工布贴紧。然后提高与试样底部相连的进水管水头,使进水管与排水管的水头差在l m左右。打开进水管与排水管阀门,使水在水头差的作用下从底部进入试样,从试样的顶部流出,排除试样内的空气,直到流入水量与流出水量相等,可以认为试样已经饱和。试样饱和后关闭进水管阀门,对其施加要求的围压,待排水管读数稳定后即认为固结完成。
由于不加土工布的三轴试验橡皮膜易刺破,因此对比试验只能在相对较低围压下进行,故分别进行围压为50,100,150,200,300和400 kPa的常规三轴固结排水剪切试验,高围压下土工布对试样强度特性和变形特性的影响可由低围压下的规律类比得出。
2 试验结果分析
2.1 强度特性分析
表3围压与峰值强度的关系
Tab.3 Relationships between confining pressure and peak strength
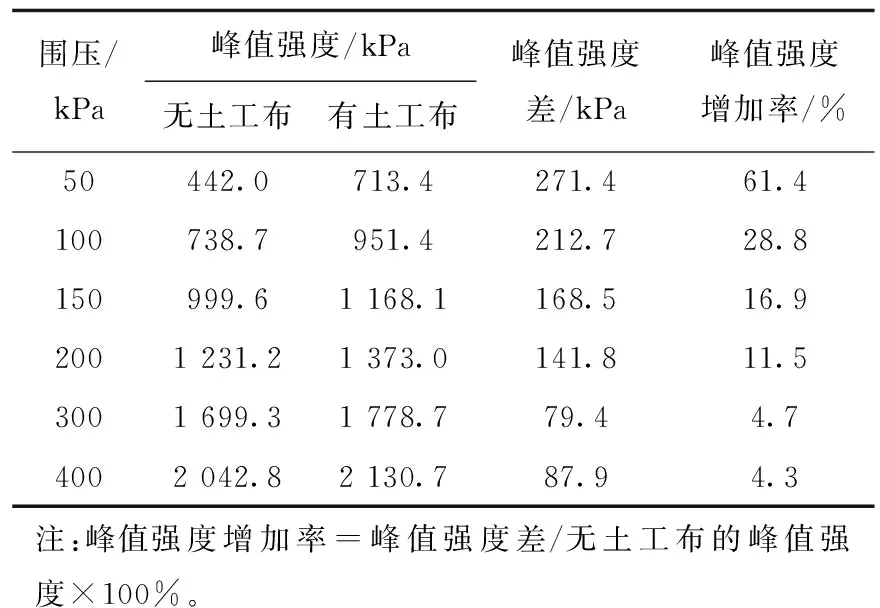
围压/kPa峰值强度/kPa无土工布有土工布峰值强度差/kPa峰值强度增加率/%50442.0713.4271.461.4100738.7951.4212.728.8150999.61 168.1168.516.92001 231.21 373.0141.811.53001 699.31 778.779.44.74002 042.82 130.787.94.3注:峰值强度增加率=峰值强度差/无土工布的峰值强度×100%。
2.1.1峰值强度 图1给出了包裹土工布与未包裹试样的应力应变对比曲线。由图1可见,在相同围压下,包裹土工布试样的应力应变曲线位于未包裹土工布试样曲线的上方,说明包裹土工布提高了试样强度。因此,在实际工程中,施加相同的σ1-σ3,包裹土工布条件下产生的轴向应变ε1比未包裹土工布条件下的要小。
表3总结了各围压下包裹土工布与未包裹土工布试样的峰值强度,即(σ1-σ3)f。当围压为50 kPa时,包裹土工布试样的峰值强度比未包裹时提高了61.4%,但是随着围压的增加,两组试样之间的峰值强度差值显著减小,且差值所占的比例也快速减小;在围压为400 kPa时,峰值强度仅仅相差4.3%。根据这一趋势,绘制了峰值强度增加值与围压之间的散点图,发现两者之间的关系可以利用幂函数进行拟合(见图2),相关系数R2=0.982。由此可以推测,当围压更高时,可认为两组试样的峰值强度相等,即土工布对于峰值强度的影响可以忽略。
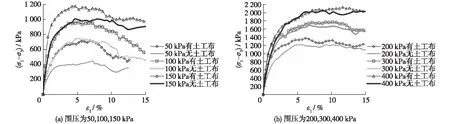
图1 (σ1-σ3)-ε1关系对比曲线Fig.1 Relationship curves of (σ1-σ3)-ε1
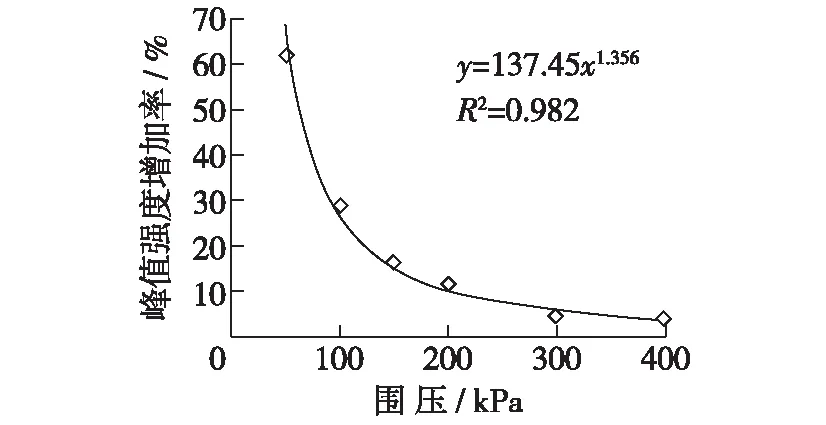
图2 峰值强度增加率与围压的关系曲线Fig.2 Relationship between increase rates of peak strength and confining pressure
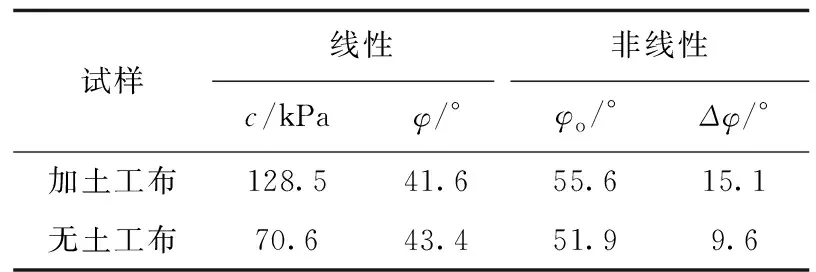
Tab.4 Comparison between strength indexes with or without geotextile
试样线性非线性c/kPaφ/°φo/°Δφ/°加土工布128.541.655.615.1无土工布70.643.451.99.6
2.1.2强度指标 通过表3中的围压及峰值强度,计算得到包裹土工布与未包裹土工布试样的强度指标见表4。从表4可以看出,线性情况下,包裹土工布试样的黏聚力c是未包裹土工布试样的1.8倍,而内摩擦角φ则减小了1.8°;非线性情况下,包裹土工布试样的φ0是未包裹土工布试样的1.07倍,Δφ增加了5.5°。
综上所述,土工布对不同围压下试样的峰值强度及土体强度指标都有不同程度的提高。其原因在于,当试样发生侧向变形时,包裹在试样表面的土工布会被拉伸,从而产生限制试样变形的应力,本质上等同于对试样施加了附加围压。当试验围压较小时,附加围压所占的比例较大,因而能显著提高峰值强度;当试验围压逐渐加大时,附加围压所占比例逐渐减小,对峰值强度的提高效果也显著降低直至可以忽略。针对本文的粗粒料和土工布,是否包裹土工布的界限围压可以确定为400 kPa(400 kPa及以下时不需包裹土工布),因为此时峰值强度差仅为4.3%,且无土工布时橡皮膜也不会被刺破。
2.2 变形特性分析
2.2.1体积变形 图3给出了包裹土工布与未包裹土工布试样的εv-ε1对比曲线。由图3可见,随着轴向应变ε1的增加,试样的体积应变εv从剪缩向剪胀发展。在相同围压下,包裹土工布试样的εv-ε1关系曲线位于未包裹土工布试样曲线的下方,说明包裹土工布提高了试样的剪胀性,即产生相同的轴向应变εa,包裹土工布条件下产生的体积应变比未包裹土工布条件下的大。
表5总结了各围压下包裹与未包裹土工布试样在轴向应变ε1达到15%时的体积应变。由表5可见,围压为50 kPa时,试样产生的体积应变较大,包裹土工布试样的体积应变比未包裹土工布试样的体积应变在数值上提高了16.25%,但是随着体积应变数值的减小,体变变化率显著增加;在围压为400 kPa时,试样产生的体积应变较小,体变变化率达到了122.53%。但是,体积应变差在此过程中变化较小,在不同围压下基本维持在1%(体积应变差的平均值)。

图3 εv-ε1关系对比曲线Fig.3 Relationship curves of εv-ε1

围压/kPa体积应变/%无土工布有土工布体积应变差/%体变变化率/%围压/kPa体积应变/%无土工布有土工布体积应变差/%体变变化率/%50-7.93-9.241.3116.52200-4.04-5.211.1728.96100-7.48-8.350.8711.64300-2.52-3.400.8834.92150-5.50-6.410.9116.55400-0.71-1.580.87122.53注:体变变化率=体积应变差/无土工布的体积应变×100%。
2.2.2侧向变形 图4给出了包裹土工布与未包裹土工布试样的ε3-ε1对比曲线,由图4可见,包裹土工布与未包裹土工布试验得到的ε3-ε1曲线都具有以下特征:侧向应变ε3都是负值,即侧向都发生膨胀。在相同围压下,包裹土工布试样的ε3-ε1曲线位于未包裹土工布试样曲线的下方,这说明在相同的ε1下,包裹土工布条件下的侧向膨胀量比未包裹土工布条件下的大。
表6总结了各围压下包裹与未包裹土工布试样轴向应变ε1达到15%时的侧向应变。由表6 可见,包裹土工布试样与未包裹土工布试样的侧向应变差以及侧变变化率随着围压的变化,没有发生显著改变,分别维持在0.5%(侧向应变差平均值)和5.17%(侧变变化率平均值)。
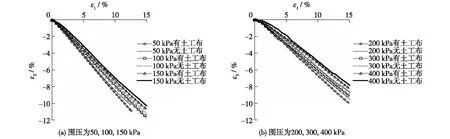
图4 ε3-ε1关系对比曲线Fig.4 Relationship curves of ε3-ε1
综上所述,土工布致使试样的体积膨胀和侧向膨胀都有一定程度的增加,且增加的量受围压的影响较小。理论上讲,土工布增加了对试样变形的约束,体积膨胀变形、侧向膨胀变形都应该减小,包裹土工布试验的εv-ε1关系、ε3-ε1曲线都应在未包裹土工布试验的相应曲线的上方,但本试验得出的结果恰恰相反,袁铁柱[12]也得出了与本试验相同的结果。笔者分析认为,土工布的增加,只是包裹试样一周,并没有缝合,提供的侧向约束有限;但是,土工布阻挡了橡皮膜向土颗粒间嵌入,即减小了橡皮膜的嵌入量,使得测得试样排出水的体积减小,即体积应变εv在数值上是减小的,而侧向应变ε3是通过ε3=(εv-ε1)/2换算得到的,所以ε3在数值上也是减小的。

表6 围压与侧向应变(ε1=15%)的关系Tab.6 Relationships between confining pressure and lateral strain (ε1=15%)
3 结 语
用中型三轴仪对包裹土工布与未包裹土工布的粗粒料试样进行了常规三轴固结排水剪切试验,研究了土工布对其强度特性和变形特性的影响,得到如下结论:
(1)三轴试样包裹土工布后,对试样的强度影响较大,低围压下的影响不可忽略;试样包裹土工布对其体积变形也有显著影响。
(2)对于相同的σ3,包裹土工布的试样的(σ1-σ3)-ε1关系曲线位于未包裹土工布试样曲线的上方,包裹土工布提高了试样强度。
(3)包裹土工布与未包裹土工布试样的峰值强度差在低围压下较大,但随围压的增加呈幂函数形式减小,直至接近于0。
(4)线性情况下,包裹土工布试样的黏聚力c是未包裹土工布试样的1.8倍,而内摩擦角φ则减小了1.8°;非线性情况下,包裹土工布试样的φ0是未包裹土工布试样的1.07倍,Δφ增加了5.5°。
(5)对于相同的σ3,包裹土工布试样的εv-ε1,ε3-ε1关系曲线位于未包裹土工布试样曲线的下方,包裹土工布限制了橡皮膜的嵌入。
(6)包裹土工布与未包裹土工布试样的体积应变差和侧向应变差受围压变化的影响较小。

