SIFT特征匹配算法研究

王玥

（广西科技大学鹿山学院，广西柳州，545616）

0 绪论

近些年来，图像匹配技术已经在图像处理领域占据了重要的席位，被用在图像的拼接上、遥感文字的识别上、医学影像的分析上等等。能够研究出一种可以普遍应用的，甚至通用的，而且在匹配上具有速度快、准确的匹配技术有很高的现实意义。而在众多的匹配技术当中，特征匹配技术因为复杂度较低而且具有较高的鲁棒性得到了业界的重视和快速发展。尤其是其中的SIFT算法因为在尺度上、图像旋转上、图像亮度上有一成不变的特殊性，而且对于其对视角的不同、声音的不同等也有很高的鲁棒性，所以SIFT算法在特征匹配技术中也有很高的研究价值。

1 SIFT特征匹配算法的实现

SIFT特征匹配算法的要实现，必须包括两点：一是提取特征点，二是如何匹配。

其中特征点的提取包括：

■1.1 将彩色图像转为灰度图像

为减少算法的实现复杂度，把彩色图像通过三通道的RGB空间映射到单通道的灰度空间，通过以下的公式进行：

其中公式右边的R、G、B就是彩色图像的一个像素的三个通道的值，而公式左边的G就是这个像素点的灰度值。

■1.2 利用高斯函数进行尺度空间极值点的提取

尺度空间这一概念最早出现在计算机视觉领域，为使计算机能模仿人眼的处理过程对场景进行分析，通过对图像进行多尺度模糊处理，图像模糊度逐渐变大，从而模仿人眼观察物体时由近到远的过程。通过这样多尺度的处理分析，从而使计算机能够分析出物体的实际大小。为了使提取出的关键点具有尺度不变性，就需要借助多尺度空间来实现。首先我们设σ为尺度参数，其次构建尺度空间，这时我们利用高斯函数的σ依照次序分别和原始图像中的I ( x,y)进行卷积，得到图像的高斯尺度空间 L ( x,y,σ )。另外公式（3）中的x、y是代表了图像某个像素点的坐标，这时σ的值的大或者小就决定了图像的清晰度，σ的值越是大，图像中的细节越少，那么图像就越不清晰，反之图像就越清晰。

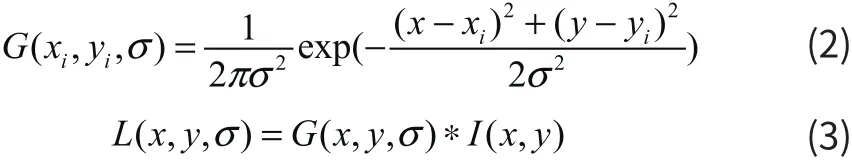
其中极值点的提取需要在高斯差分金字塔（简称 DoG金字塔)内进行，另外需要降采样和高斯模糊来构建高斯金字塔。什么是降采样呢，就是把图像的长和宽各降为一半之后再进行采样。什么是高斯模糊呢，就是对上述的采样进行模糊。在金字塔中，把长和宽相等的图像作为一组，组中的每一张图像作为一层。再有在每组的最下面的一张图像都是由前面那一组的第三层降采样形成。另外金字塔中每个相邻的两层图像进行减法，就会得到金字塔的尺度空间。高斯差分金字塔的构建，能够减少亮度差对得到的特征点的影响。之后在其中搜寻极值点。然后把每个像素点与其同层的8个点和相邻两层的各9个点进行比较，如果这个点都大于或者小于进行比较的点，我们就认为这个点事一个局部的极值点。尺度空间内的局部极值点，保证了特征点的尺度不变性。

■1.3 关键点精确定位

其实，通过以上的步骤进行操作得到的极值点不一定就是真正的极值点。所以还需要进行检测，确定是不是真正的极值点（利用三维二次函数来检测）。并且为筛选出关键点中不稳定的特征点，还需要利用子像素插值法来去除低对比度，利用二乘以二的Hessian矩阵来去除边缘效应。

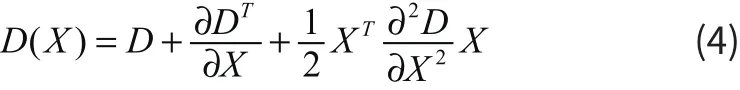
X(x,y,σ)T是前文提到的极值点，其中的x和y表示的是这个点的位置坐标，其中的σ代表的是尺度大小。把等式等于零，并对(4)式求导，就可以找到真正的极值点的位置。

去除边缘有较强响应力的点。使用α和β分别表示矩阵 H 的特征值，α=λmax为最大特征值，β=λmin为最小特征值，且 α= rβ 。

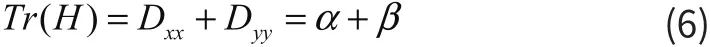
从公式（8）可以看出，只有在α和β相等的时候得到的结果是最小的，而且只要α和β的差值增加，那么比值就会增大，这就说明了在某个方向上的梯度值大，相反方向的梯度值就小，这就与边缘的特征不谋而合。所以我们要设置一个阈值，当大于这个值的时候，就可以将边缘响应点给剔除掉。

■1.4 关键点之方向赋值

为了抵消图像在旋转时会对特征匹配产生的影响，需要采取为每个特征点设置一个方向的方法使关键点对图像的旋转具有不变性。我们可以通过以下两个公式并且以特征点为圆心，以3 × 1.5σ 为半径来计算像素点的梯度大小和方向。

通过梯度直方图来计算邻域像素的梯度和方向，范围是零到三百六十度，并且每隔九度一个柱，一共有三十六个柱，这样就有一个36维的梯度向量。其中的每个维就表示这个方向的大小。梯度直方图的最高值就表示是这个关键点的邻域的主方向，也是这个关键点的方向。

■1.5 关键点之描述

得到局部特征点后，关键的步骤就是要利用这个局部特征点将其周围区域的信息描述出来，由此可以减少关键点受视角、旋转、光照等影响。通过关键点的方向赋值，我们已经能够得到关键点的主方向。以关键点为圆心，取随意大小的半径，并使区域旋转到主方向，这样的关键点就有了旋转不变性。另外，我们把区域分成四乘以四的子区域，而且在每个子区域里面进行八个方向的梯度直方图进行计算统计，这样就形成了四乘四再乘八等于一百二十八维的SIFT描述子。

2 SIFT特征点的匹配

在参考图像和待匹配图像中都进行 SIFT 特征点提取之后，我们就可以对这些特征点进行匹配了。判断两个 SIFT描述子的相似程度的方法我们通常选用描述子间的欧氏距离来表示。我们用欧氏距离来对参考图像和特征匹配图像进行SIFT特征点匹配。

Ri= （ri1,ri2,...,ri128）是参考图中的SIFT描述子向量，Si=(si1,si2,...,si128)是匹配图中的SIFT描述子向量，d是两者间的欧氏距离。

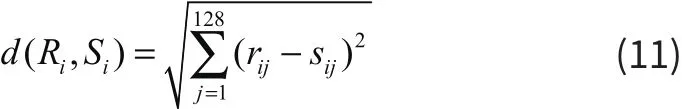
利用以上的计算和统计，就可以得到与这个描述子最近的和次近的距离。然后我们就可以用次近距离和最近距离的比的结果来看是否匹配。如公式(12）。假设一个阈值TDis，如果比值小于阈值，就匹配成功；若比值大于阈值，就匹配不成功。另外，这个阈值取值范围是 0. 6<=TDis<=0.75 。Min｛Dis｝表示描述子的最近距离，SecMin｛Dis｝表示描述子的次近距离。

尽管SIFT算法具有抗尺度、旋转、亮度变换，具有高鲁棒性，但是它抗仿射变换性能不是很理想，有待进一步完善。