基于能量网络理论的区域综合能源系统运行优化研究

李 明，陈皓勇，邱 明，黄 龙，陈思敏

(华南理工大学电力学院，广东 广州 510641)

0 引言

随着经济科技的迅速发展，人类社会对于能源的需求急剧上升。这直接导致了煤炭、石油等常规化石能源资源的迅速枯竭，并由此引发了全球范围内人类对于资源环境能否持续发展的担忧。世界各国开始探索一种能够提高能源的利用效率，适应可再生能源的开发利用并优化各类能源的统筹分配以实现可持续发展的新途径[1-2]。综合能源系统(integrated energy system, IES)以其能量转化设备(如热电联产机组、热泵及循环泵等)为纽带，通过供热网络、电力网络及供气网络等能源子网间的能量流动及互补，可有效实现能流的合理分配，并提升能量的利用效率，无疑将成为未来能源领域的发展方向[3]。

国内外对于综合能源系统的研究，目前主要集中于IES耦合多能源系统的稳态潮流求解、IES优化规划方法及IES市场经济理论等几个方面。文献[4]基于能源集线器模型，构建了热电联产系统模型，针对区域综合能源系统(regional integrated energy system，RIES)的完全耦合、部分耦合及完全解耦3种运行模式，形成了适用于含电/气/热等3种能流的RIES稳态潮流求解方法。文献[5]建立了考虑安全约束的电-气最优潮流，该模型在求解最优潮流时考虑了系统发生N-1故障的情况，通过灵敏度分析可快速得到稳定的故障应对方案，避免线路过负荷。文献[6]考虑风力发电并网带来的不确定性以及天然气管道气压安全约束问题，建立了一个电-气耦合IES的二阶段鲁棒发电日前调度模型，通过分段线性化方法处理了燃气管网气流约束的非线性，提高了算法的收敛性。文献[7]针对IES的设备选型、设备容量配置及系统运行策略的整体优化，设计了一种冷热电联供系统的三级协同整体优化方法，并提出一种“以电定热”和“以热定电”混合运行策略，实现了系统产能以及用能的良好匹配。而在市场经济理论部分，吴利兰等人提出了一个基于多主多从Stackelberg博弈的能源交易模型，通过分析IES中多个分布式能源站和用户之间的多种能源的交互方式，求解它们之间的均衡交互策略，通过竞争决定能源价格，从而实现各自收益的最大化[8]。

在IES理论研究方面，大量学者开展了深入的研究，并取得了丰硕的成果。然而，当前大多数的研究通常只涉及2种能量的耦合，同时各网络模型均是基于分立的异质能流系统建模机制而开展的，不同的能流领域沿用本领域当前典型的能量潮流计算方法。不同领域的模型互换性差，数据表达不统一，在时间尺度统一及数据交换方面存在困难，影响IES的统一建模及分析。为此，本文从能量网络理论出发，基于能量公理化的思想，建立流体网络及热力网络传输的等值电路模型；随后结合能量转换设备模型，实现多能流耦合系统的统一建模，并以IES稳态能量潮流作为IES优化模型的等式约束进行优化；最后，以所搭建的模型对某岛屿RIES进行建模，同时以RIES能量损失最少为目标，通过粒子群寻优算法实现该岛屿RIES的运行决策优化。

1 IES网络等值模型

1.1 能量网络理论

作为能源互联网的关键组成部分，综合能源系统是典型的多能域耦合系统，是能量网络理论的研究对象。能量网络理论从能量角度出发，以能量作为不同物理过程之间相互耦合的桥梁，研究不同形式能量的传递、存储及转化的普适化规律，应用集总参数的分析方法，实现异质能流子网络的融合分析[9]。

为实现不同能流系统的统一描述，能量网络理论将综合能源系统的异质能流子系统的状态变量统一使用广延量及强度量来表述：广延量指在状态变量中与物质的量密切联系的，且具有可叠加性的量，典型的广延量包括熵、体积等；而强度量则为状态变量中不随物体物质的量变化而变化的，且不具有加和性的量，典型的强度量包括温度、电压等。

考虑能量传递过程是1维的，且传输过程中不发生泄漏，以工程中常用的圆管传输为例，能量的空间平衡方程可简化为

(1)

式中：E为管道中的能量；Hx为流经截面的广延量x的流率，为流量密度Jx和管(线)面积之积；X为强度量；下标A和E分别为传递线(管)路的首端和末端截面积；xg为传递过程中自发产生的、与长度L相关的广延量的函数。

式(1)中，等式左边的表达式是该圆柱形传递线(管)路中的能量因广延量流动产生的变化率；右边的第1项和第2项是流经管道横截面的广延量所携带的能量之和，第3项是传递过程中因过程不可逆出现的能量耗散，第4项是管道中自发生成的广延量产生过程中释放的能量。此外，由分析力学的基本知识可知，能量传递转换过程中还会产生广义动能(惯性现象)和势能(弹性现象)及其相互转化[10]。在稳态传输情况下，暂时忽略能量传递的弹性和惯性现象。

1.2 传输管线等值模型

虽然不同形式的能量传递过程从物质形态角度来看存在巨大差异，但从介质流的角度来看却呈现一定的规律性，如描述导电过程的欧姆定律、描述粘性流动的牛顿定律和描述热传导的傅里叶定律，其形式具有一致性[11]。传递公理指出，在相应基本强度量差的推动下，基本广延量实现流动运输[12]。广延量的传递规律可描述为

Jx=KF=-KX

(2)

式中：F为促使基本广延量流动的驱动力；K为基本广延量的传递系数；X为共轭的基本强度量之差。

1.2.1 电能传递的能量网络等值模型

对于电力网络，能量流密度Jx实际上就是电流的密度，强度量X为电势。因此，当系统以直流形式平稳供电时，根据式(2)，可求得电流的通式：

Hx=JxA=-KAX⟹HxdL=-KAdX

(3)

式中L为传输线(管)路的长度。再对式(3)两边进行积分，于是有

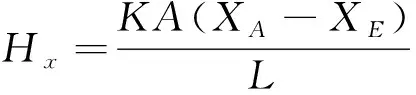
(4)

如此，式(4)的含义就十分明显了：Hx为电流，而(XA-XE)则为电线首末端的电压差；K为基本广延量的传递系数，在此表示电导率；A为导线的面积。这便是熟悉的欧姆定律。

由于电力系统在这方面的研究比较成熟，本文直接沿用交流电力系统，即动态情况下的能量网络的计算方法。其能量网络节点方程如下式所示，未知量为节点的强度量。

H=YX

(5)

式中：Y为能量网络节点导纳矩阵；H和X分别为支路电流向量和支路电压向量。

1.2.2 压能传递的能量网络等值模型

压能传递过程中，强度量是压强p，基本广延量流是体积流率Jv。由质量守恒定律可知，质量的源强度gm=0。结合比体积V与密度ρ的关系式V=ρ-1，推导可得随体形式的体积平衡方程[13]：

(6)

同理，可对式(2)作如下变换：

(7)

根据流体网络理论，有如下方程组：

(8)

式中：A为流体网络的关联矩阵；Bf为流体网络基本回路矩阵；H为支路流量；Φ为流经负荷或热源的流量；ΔX为支路两端的压强差。

1.2.3 热能传递的能量网络等值模型

热能传递过程中，以温度为强度量。同时由热力学第二定律可知，在一个与外界不存在相互作用的系统中，熵永不自动减少。在不可逆过程中，系统由不平衡状态过渡到平衡状态，熵单调增加，即熵的源强度gs≠0[15]。此时以熵作为基础广延量将带来诸多不便。

定义He=XHx为能流(在热能传递过程中He即热流量)，λ=KX为热传输系数，并根据连续性原理，假设能量的耗散现象只存在于管线的径向，则可对式(2)作如下变换：

(9)

式中：下标e为热耗散；下标r1与r2分别为热传输管道的内径与外径；Re即为热流量传输的热阻。

取圆柱形管路始端温度Xin及末端温度Xout的平均值作为管道平均温度Xav，可得

(10)

根据式(9)所描述的管道内部的热量平衡关系，有

(11)

式中：cp为水工质的比热容；m为质量流量；下标in和out分别代表流入与流出；X0为环境温度。

联合式(10)、(11)，得

(12)

由于热能传递同压能，电能等传输过程相差甚远，在能流汇集节点，当来自不同管道热流载体混合时，热流载体的温度将迅速统一。其热量平衡关系可描述为

∑mout)Xout=∑(minXin

(13)

1.3 能量耦合元件模型

1) 热电联产机组是当前应用较为广泛的一类能量转换设备，它通过合理分配汽轮机内高压蒸汽及乏汽的去向，使得发电和供热能同时进行。热电联产机组一般分为燃气轮机式机组、往复式内燃机机组和抽汽式机组。其中，燃气轮机式、往复式内燃机等热电联产机组的功率表达式为

(14)

该类机组为定热电比，cm为热电比率，φ为机组输出热量，P为机组输出电功率。

抽汽式热电联产机组的功率表达式由下式描述：

(15)

该类机组为变热电比，pcon为全冷凝模式下的输出电功率，Z为常数。

2) 管道中热水的流动需要克服阻力，消耗压能。为维持一定的压强，需要循环水泵消耗的电功率Pp为

(16)

式中：mp为送水量；ηp为泵效率；Hp为网络的泵压；g为重力加速度。

3) 热泵消耗少量的电能把环境中的低品位热能提升至高品位，热泵的能效系数表达式为

(17)

式中：φrb为热泵的供热功率；Prb为热泵的功率消耗值；COP为热泵的能效系数，其值大小随热源和热负荷之间温差的变化而变化。

2 IES优化模型与求解

2.1 优化模型

本文采用粒子群算法针对综合能源系统进行优化，模型的优化目标为系统的总能量损失最小，此外，综合能源系统中还应该对变量进行约束。

1) 目标函数。

本文基于单目标函数来优化综合能源系统，以系统的总能量损失最小为目标函数。

(18)

式中：Ploss为电力系统的有功损失，其值等于输入功率之和与输出功率之和的差值；Qloss为供热系统的热能损失，其值等于输入热能之和与输出热能之和的差值；Lloss为供热系统的压强损失(包含供回水管路)；Shl为供热系统的管路集；HVi为流体管道内的广延量流；RVi为管道流阻。

2) 等式约束。

综合能源系统包含电力系统和供热系统，因此也存在着相应的等式约束，如：电力系统的潮流平衡方程、管道的热力平衡方程、管路压力方程、供热温度和回水温度方程。由式(1)可知，稳态情况下式(1)左端为0，同时右端第4项源项为0，则可得支路的能量平衡方程。于是，模型中的等式约束数学表述如下：

(19)

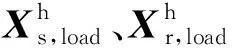
3) 不等式约束。

对于该综合能源系统的优化模型，本文考虑控制变量有：发电机的端电压大小Xe,G、变压器分接头投切位置Tap以及供热系统中供热点的热水供应温度Xh,supply，不等式约束表述如下：

(20)

式中:上标max、min分别表示该控制变量调节范围的上下限；SG、STap、Ssource分别为所有发电机组集合、变压器分接头集合、供热点集合。

系统中的状态变量随控制变量变化而改变，包含电力系统各负荷节点电压幅值Xe、发电机产生的无功功率QG、管路的流量大小HV以及供热系统中负荷节点热水供应温度Xh,s。不等式约束表述如下：

(21)

式中，各状态变量受相应的集合约束，SPQ、SG、Shl、Shload分别为PQ节点集合、发电机组集合、供热系统管路集合、热负荷集合。

2.2 粒子群算法

本文通过粒子群算法来求解某综合能源系统的优化模型，该算法源于生物捕食行为的分析，动物间通过集体的分工协作及信息共享使得种群能够快速寻优。假设模型中待求的问题解都可表示为粒子，对于这些粒子，在一个N维的空间内搜索，赋予每个粒子速度和位置的特征，通过自身信息以及和其他粒子的对比获得最终的调整方向。

粒子群算法流程如图1所示。

图1 粒子群算法流程图Fig.1 Flow chart of particle swarm optimization

使用粒子群算法时，粒子群算法包括粒子的速度、位置变量以及适应度函数。在该运算场景中，综合能源系统的适应度值函数设定为总能量损失的倒数(总能量损失最小时，适应度值最大)，粒子的位置变量对应系统中的控制变量(包括变压器分接头位置、机组机端电压和热水供应温度)，粒子的速度变量对应变量的变化值，粒子位置可表示为(x1,x2,…,xm)，粒子速度表示为(v1,v2,…,vm)，m表示该综合能源系统具有m维变量。迭代过程中，每代更新当前粒子对应的控制变量信息，通过目标函数值与适应度值反映当前优化参数的优异性。

3 算例分析

本文针对为某岛屿提供电力和热的综合能源系统进行分析，该综合能源系统如图2所示[16]，其中电力网络节点负荷、供热网络节点负荷分别如表1、2所示。电力网络和供热网络通过3台热电联产机组、循环水泵等互联实现能量的耦合。

图2 某岛屿综合能源系统Fig.2 An island integrated energy system

表1 电力网络节点负荷Table 1 Load buses in power network

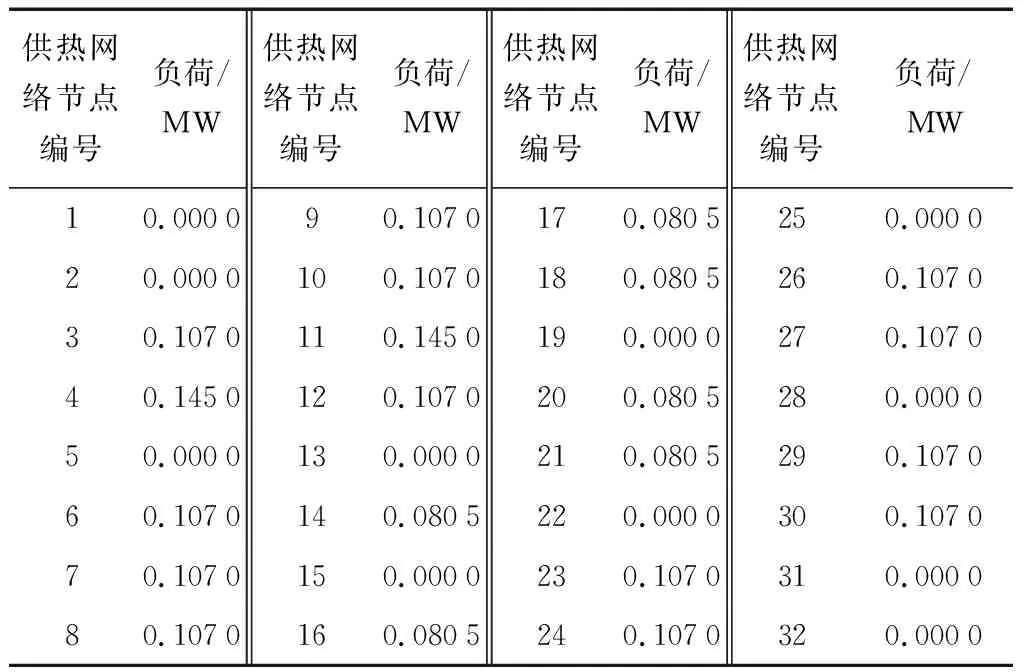
表2 供热网络节点负荷Table 2 Load buses in thermal network

在图2中，机组G1、G2、G3分别为燃气轮机机组、抽汽式汽轮机机组和往复式内燃机机组，电力网络包含9条母线和5处负荷，供热网络包含32个节点和32条管路。算例的状态变量和控制变量情况分别如表3、4所示。

本例中粒子群算法的维数为7，设定粒子群算法学习因子c1和c2为2，惯性因子w为1，算法的迭代次数为60，粒子数为40。

表3 算例的状态变量情况Table 3 State variables in case

表4 算例的控制变量情况Table 4 Control variables in case

图4 电压相角与幅值对比Fig.4 Comparison of voltage angle and amplitude

1) 迭代曲线。

算例中，所选择的适应度函数为系统能量损失的倒数，通过描绘群体中每代最佳适应度值可以得到算法的收敛特性。图3为粒子群算法迭代60次的迭代曲线，可得知系统优化后的能量损失降至0.087 9 MW，其中热能损失为0.079 5 MW，电能有功损失为0.005 8 MW，压能损失为0.002 6 MW。

图3 算法迭代曲线Fig.3 Iterative curve of algorithm

由图3可知:应用粒子群算法进行计算，每代粒子的适应度值如黑点所示；将黑点连接起来便形成算法收敛特性曲线，其反映算法的收敛趋势；该算例的适应度曲线在迭代20多次后达到最优，因此其具备较强的收敛能力和较快的收敛速度。

2) 结果对比。

通过粒子群算法可获得目标函数最优值和控制变量的优化值，在该最优粒子结果下，该综合能源系统的电压相角、电压幅值、管道质量流量及供应(返回)温度在优化前后的变化分别如图4—6所示。

由图4可看出，通过粒子群算法计算所得优化后电力系统中各节点的电压相角值有所改善(向0趋近)，而电力网络的节点电压幅值接近于1 pu，说明粒子群算法优化的方向能够有效降低系统的有功损失，同时也增加了电力系统运行的稳定性与可靠性。

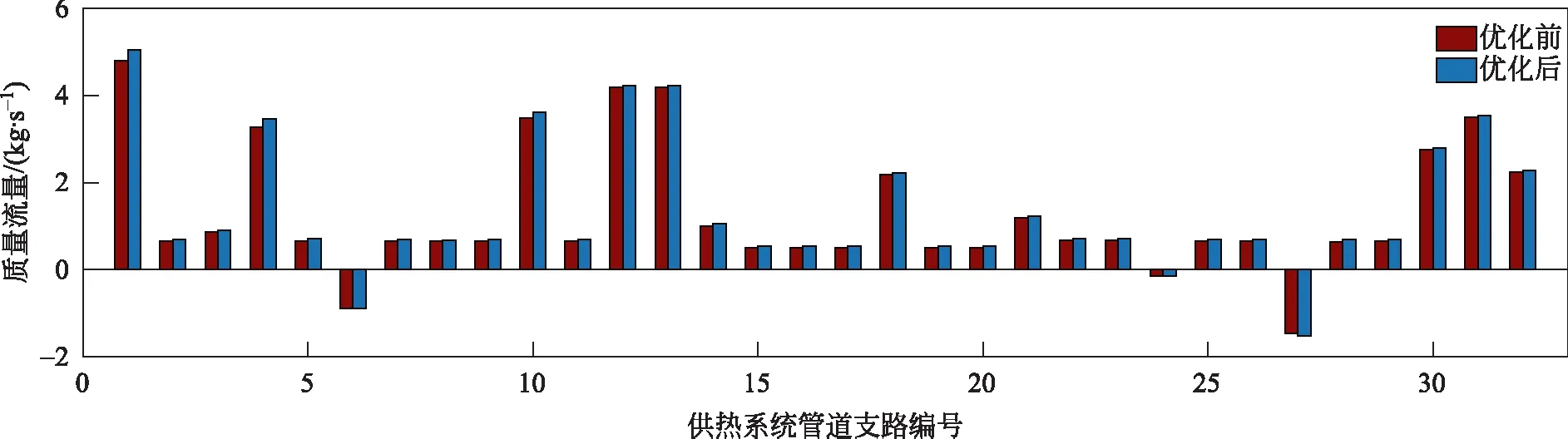
图5 质量流量对比Fig.5 Comparison of mass flows

图6 节点温度对比Fig.6 Comparison of nodes’ temperature

图5中质量流量的正负代表管道流量的流向，可见利用粒子群算法优化后部分供热系统管道内的质量流量较优化前有所增加，同时不影响管路内流体的流向，说明采用粒子群算法寻优能有效改善原管道内的流量分布，从而减小管道内的热能损失。

图6中，优化前后供热系统节点的供应温度有所下降(受限于用户侧温度变化)，返回温度值基本不变，使得在用户侧热负荷满足需求的前提下，能较大程度地降低热水流经管路中所造成的热量损失，从而减小了能量的总损失。

采用综合能源系统优化模型后，该系统的安全裕度得到有效增加，增强了系统的安全可靠性；在系统参数变化不大的情况下，原小岛综合能源系统的能量损失为0.095 1 MW，经优化后能量损失为0.087 9 MW，系统能量损失的下降比例达到7.571%，有效地提升了综合能源系统的能量利用效率。

4 结论

随着能源技术的高速发展，传统的供能网络面临的挑战也日益加深，IES概念的提出，使其结构与功能更是日趋复杂与异构。未来的供能领域，多能流耦合已经成为了IES的显著特征，为了优化IES的规划调度，得到其整体性能的准确运行模拟，必然要进行多能流系统的统一建模以及运行模拟。

本文从能量网络理论出发，基于能量公理化模型完成了某32节点综合能源系统的最优能量潮流计算。从结果来看，所建模型在减少IES运行过程的能量损耗方面具有显著的效果。然而，该模型在改善热力网络能量潮流分布的过程中，也一定程度加大了压能(即电能)的损耗。就能量品质及价值而言，电能远大于低品质的热能。这无疑有悖于IES的“能质匹配”原则。