ISM模型在数控机床装配过程质量评价的运用

梁 迪, 钟彦恺, 王 记

(沈阳大学 机械工程学院, 辽宁 沈阳 110044)

数控机床作为现代工业经济的顶梁柱之一,其质量评价体系的建立有着举足轻重的地位,然而现阶段相当一部分的机床质量不达标,其中很大一部分原因是由于数控机床装配过程中存在的问题导致的.传统的质量评价一般采用SPC(Statistical Process Control)方法对装配过程中的每一步进行测试,然后运用鱼骨图对数控机床装配过程中产生的问题进行分析,形成质量影响因素A[1].然而如何把对影响质量的因素结合在一起,并确定这些因素的排序一直是个问题.由于缺少可量化的数学模型和一定的科学计算,使得对装配质量问题产生的影响因素和层次的分类不明确.

现代系统工程中为解决复杂问题常常运用多种模型算法,如珩磨辊辊形曲线的解析求法和田口方法在主轴系统参数设计优化组合方面的应用等研究均应用到了复杂模型[2-3].解释结构模型是针对较复杂系统结构的各组成因子进行描述的一种模型,简称ISM(Interpretative Structural Modeling Method).其原理是先将庞杂的系统分解成为若干个子系统要素,根据人们的实践经验运用算法模型最后构架出阶梯型的模型结构.

1 数控机床装配过程质量波动传递和转化模式

装配是使用严格的工艺技术将各种合格的零件组合成质量达标产品的过程[4].由于数控机床的零件数量通常可以达到上万个,而不同层次的数控机床的复杂程度也不相同,于是在数控机床的装配过程中一般将数控机床划分为零件、套件、组件、部件、整机5个单元[5].所以数控机床的装配过程即是把若干个零件组合成套件,再将若干个套件组合为组件,依次最终将所有单元组合在一起形成整机,如图1所示.

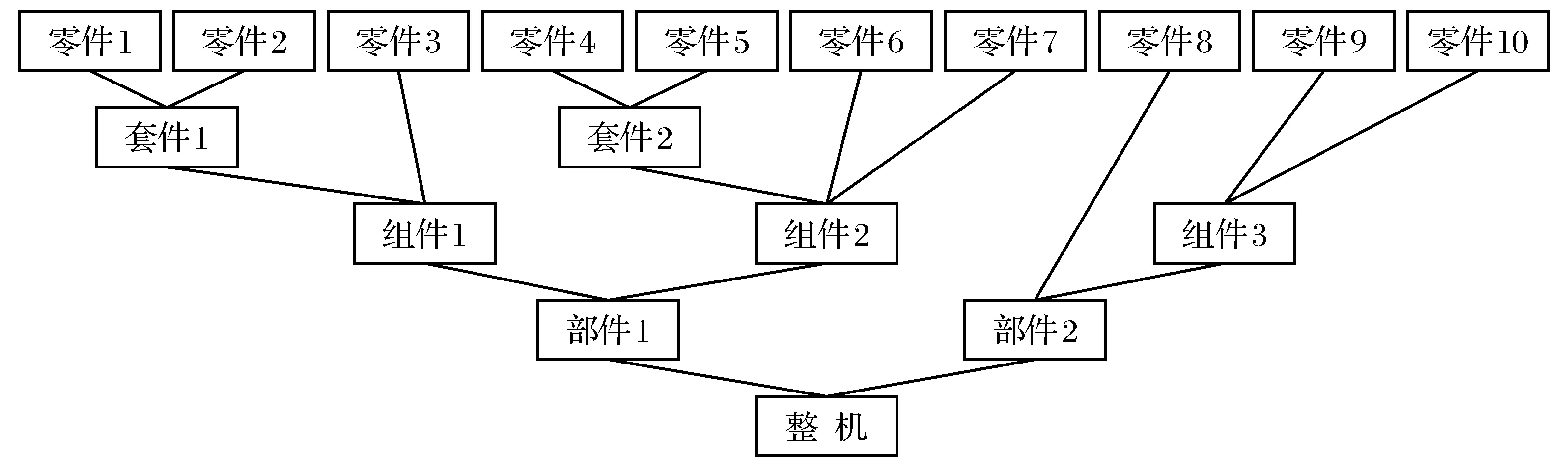
图1 数控机床的装配过程图Fig.1 Assembly process diagram of CNC machine tools

数控机床的质量问题会严重影响机床的使用寿命和稳定性.这些问题是机床在装配过程中一步步叠加形成的.在装配过程中,每道工序的输出数据对下道工序的影响都是至关重要的,因此必须要尽量减小每道工序的误差,才可以最小化机床的质量问题.例如装配体的每个零件自身数据是否精确和零件之间连接是否在装配体的误差范围内,这些小细节都会影响下道工序的输出数据[6].图2为装配过程中逐步累积的工序误差,最终将会影响到装配完成后整机的质量.

图2 数控机床装配过程质量形成过程图Fig.2 Quality forming process diagram of numerical control machine tool assembly process

数控机床装配的质量传递波动沿“整机—部件—组件—套件—零件”的路径分解传递.在图2中,数控机床的各项指标对应各个工序组件.数控机床的装配质量是从最基础的零件质量影响因素开始逐级累积、传递,最后对整机的质量产生一定影响.

2 装配序列评价指标构建

在进行装配之前,必须先列出一个装配序列的评价指标.这对零件进行装配时的准确性与难易程度有着决定性的作用,也是对不同机床的不同装配工序的表达.传统的装配序列指标构建方法大多数是按照零部件装配的难易度和对其他的零部件的影响程度来构建.但当设备比较复杂,零部件比较多的时候,将会产生多种不同的装配序列,需要建立数学模型,并用现代的科技手段解决.假设机床上存在n个零件,理论上有n!种装配方案,除去一些肉眼可见的不可能的装配顺序后,还存在多种方案[7].所以需要对剩余的装配方案进行逐一测试,并选择对机床整体的准确性和装配质量影响最小的装配序列.

在机床装配过程中,装配序列对机床质量的影响是最直观的,可以通过装配序列的指数来判断最终选出装配方案的难易程度.机床和其加工出工件的质量都与机床装配过程中的质量问题密切相关.

由于现阶段应用的层次结构评价指标体系没有足够的科学理论支撑,本文在此基础上引用解释结构模型整理出不同种类的装配质量影响因子,找出影响装配过程存在质量问题的最直接因子,重新构建更加完整的评价体系.

3 装配序列解释结构模型的建模步骤

数控机床装配序列解释结构模型建模与分析的步骤如图3所示.

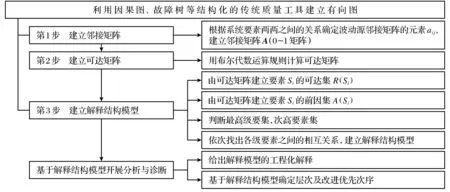
图3 数控机床装配序列解释结构模型建模与分析图Fig.3 Numerical control machine assembly sequence interpretation structural modeling and analysis diagram

第1步 建立装配质量波动邻接矩阵A.通过建立鱼骨图分析质量波动的影响因子,列出质量波动因素集S={S1,S2,…,Sn}.然后建立邻接矩阵与质量波动因素集一一对应,将Si(i=1,2,…,n)与Sj(j=1,2,…,n),即影响数控机床装配质量波动的因素集之间的关系对应起来,得到质量波动邻接矩阵A,其定义如下:如果i=j,则aij=0;如果i≠j,则:

r≤n-1,其中n为矩阵A的阶数,则Ar-1=(A+I)=R,矩阵R是1个n阶的0-1矩阵,称为可达矩阵,其元素rij非0即1,是有向图可达路径的代数表征[8].

第3步 建立装配质量波动解释结构模型.定义要素Si的可达集:

前因集

如果R(Si)⊇A(Sj),则R(Si)即为最高要素集L0;将L0所包含的要素从矩阵R中划去,在余下矩阵中重新求各要素的可达集、前因集、最高要素集(L1);重复计算多次后将依次得到各个层级(L2,L3,…);依次求得的各个层级划分后,绘制有向图,最终得出装配质量波动解释结构模型.

4 应用案例

某数控机床制造厂近日发现其产品质量波动较大, 工程师迅速成立专项小组解决产品质量波动问题. 为了精确找到数控机床装配质量波动因素, 绘制数控机床装配过程因果图, 如图4所示.

图4 数控机床装配过程因果图Fig.4 Cause and effect diagram of numerical control machine tool assembly process

装配性能稳定性指在装配过程中,装配序列在装配力、重力及各类连接关系下的稳定程度,主要与零件配合类型、零件装配关系数等因素有关.

装配过程可靠性是指按照给定的装配序列在规定条件下和规定的时间内,保证装配出来的产品具有规定可靠性水平的能力.而装配过程中,不同可行装配序列的精度保证性主要受装配过程重定向次数、装配体对称性等因素影响,保证装配精度的主要目的是使装配产品误差最小化.

装配工艺简单性表示连续装配操作过程中装配序列的工艺复杂程度,主要与装配关系数、装配操作并行性等因素有关.装配关系数反映了零部件之间相对位置和配合关系,装配关系数越大,产品的装配难度越大.

装配操作的并行性是指产品可分为多个子装配体同时进行装配,并行性越小,序列的临界装配路径就越长,相应的装配难度也就越大.

装配成本经济性主要用来度量不同装配序列对工具、夹具、机床及装配人员等资源使用情况的经济程度.对于不同的可行装配序列,其装配成本越低,经济性越好,综合质量也就越优.

装配操作聚合性指在装配序列规划时应使装配过程中相似的装配操作集中完成,以减少装夹次数和更换装配工具的次数,节省装配时间.

装配精度保证性是在正常使用条件下,机床能在较长时间内保证其精度特性以保证产品工作性能的能力.目的是保证产品工作性能.

依照数控机床的装配特点,为了反映出数控机床装配过程中的优点和缺点,决定提取15个影响数控机床质量波动的因素,如表1所示.

表1 数控机床装配质量波动因素表Table 1 Assembly quality fluctuation factor table for CNC machine tools

根据上述15个影响数控机床质量波动的因素建立邻接矩阵,用以表示这15个影响因素之间的关系.对邻接矩阵作如下定义:

建立数控机床装配质量波动影响因素的邻接矩阵:

将邻接矩阵与单位矩阵I进行求和,再运用布尔代数的幂运算求可达矩阵

经计算得:r=2,R=(A+I)2即

按照解释结构模型方法对可达矩阵划分层级,得出以下3层数控机床装配质量波动的影响因素,第1层为S11,S12,S13,S14,S15;第2层为S1,S4,S5,S7,S8,S9,S10;第3层为S2,S3,S6.最后依据数控机床装配质量波动影响因素的分层结果画出解释结构模型,如图5所示.

由图5可得知数控机床装配质量波动影响因素的层次关系,其中第1级要素便是影响数控机床装配质量波动的直接因素,采取此要素级建立数控机床装配质量评价指标体系,即:

5 结 论

本文对数控机床装配过程质量波动传递和累积模式、波动影响因素之间关系进行分析,运用图论方法将数控机床装配过程影响关系拓扑结构简化为有向图和邻接矩阵,基于布尔代数方法计算可达矩阵,建立数控机床质量波动解释结构模型.建立的解释结构模型可以弥补SPC等传统分析工具在分析质量问题时不能诊断质量波动的原因,并没有可量化的数学模型支持的缺点.所采用的ISM方法在建立质量评价体系研究方面具有一定的推广价值.