稀浓度下铁系催化剂制备过程介尺度建模与计算
,
(浙江理工大学理学院,杭州 310018)
0 引 言
在工业上,生产沉淀铁催化剂主要由沉淀、老化、过滤、洗涤、干燥、焙烧等步骤组成[1]。在第一步的沉淀反应中,溶解于溶液中的具有原子尺度的前躯体原料离子(小尺度)与沉淀剂发生化学反应,形成具有纳米尺度的晶核或簇体,然后再通过结晶生长、粒子聚集等过程,逐渐演变为具有纳米或微米尺度的一次粒子和具有三维立体结构的二次团聚粒子(介尺度过程)。在该演变过程中,粒子的尺寸、表面性质和聚集过程不断发生多尺度的变化,这些变化决定最终催化剂的结构(比表面积、孔结构)和表面晶体结构等。对沉淀法制备催化剂而言,如何调节与控制第一步的沉淀反应过程,即原始晶核或纳米簇体以固液界面为起始点的结晶和团聚过程,以及这两种变化单独或共同作用下形成具有三维立体结构的一次粒子与二次粒子的过程,是沉淀法制备催化剂过程中面临的关键共性科学问题。
自20世纪30年代后期以来,对结晶过程模型的研究引起了大量材料科学家和数学家的兴趣。以Kolmogotov等为主的学者研究了结晶过程中的统计原理,提出了KJMA模型[2-5]。该模型仅研究成核率与晶核生长速率是常数的结晶过程。Cahn[6]提出了一个改进的KJMA模型,即时间锥模型(又称为因果锥模型)。随后,Burger等[7-9]研究了在空间一维情形下,基于因果锥方法的非等温聚合物结晶的模型。Capasso等[10]在Burger研究的基础上,提出并解决了成核率决定反问题和生长率决定反问题。Liu等[11-12]研究了结晶过程中的多重双曲偏微分方程模型,证明了模型在奇数维情形下与因果锥模型等价,但是他们并没有在因果锥方法的基础上进行直接求解。Jiang等[13]研究了最终观测数据波决定源项反问题,给出逆源问题解唯一性的适定性结果,该研究可以进一步扩展到结晶过程中的生长率决定反问题等。
本文在沉淀法制备Fe基催化剂的稀浓度实验下进行数学建模与计算,仅考虑结晶过程中的成核率与生长率,由于沉淀法制备Fe基催化剂的正常浓度的实验需要考虑晶核集聚的影响,因此本文暂不讨论晶核的集聚问题。稀浓度实验的数学建模主要以KJMA模型为基础,应用因果锥方法,推广到空间三维的情形,结合宏观尺度的热扩散过程和微观尺度上的随机过程,建立耦合的抛物型方程模型,并对其进行数值仿真。
1 成核-晶核生长速率与热扩散过程耦合的数学模型
考虑沉淀法制备Fe基催化剂过程的示范性实验,即稀浓度下Fe(OH)3纳米一次粒子(晶核)的生成与生长实验。示范性实验的过程为:在95 ℃的热水中加少量Fe(NO)3,同时进行旋转和搅拌(400 r/min),便产生了稀浓度的Fe3+,又从热水中产生了很稀浓度的(OH)-,从而产生纳米级的Fe(OH)3颗粒(一次粒子),这些颗粒大小为5 nm左右。在透射电镜下发现Fe(OH)3颗粒呈现类球状,内有晶格条纹(按规则排序)。一次粒子间无规则地聚集在一起时,稀溶液条件下得到的是溶胶。示范性实验结果表明:Fe3+和(OH)-发生化学反应生成Fe(OH)3分子,通过分子集聚(按一定规律周期重复排列)形成一次粒子(晶核)。Fe(OH)3纳米粒子的透射电镜图如图1所示。本文通过数学建模给出上述实验过程的数学描述。

图1 Fe(OH)3纳米粒子的透射电镜图
1.1 微观尺度上的随机模型
假定成核过程是一个随机的空间标记点过程[14]。对于概率空间(Ξ,F,P),一般用N表示微晶的数量,即
(1)
其中:Xj是第j个核的空间位置,Sj是第j个成核发生的时间。Xj和Sj分别是Ω⊂R3和R+中的随机变量,Ω是一个Borel集。
设B+和C分别是R+和Ω中Borel集的σ-代数,若t∈R+,x∈Ω,B∈B+,C∈C,则B+×C上的Direc测度ε(x,t)为

(2)
因此N是B+×C上的整数值随机测度。设N(A)为时空区域A∈B+×C中的成核事件数,即
N(A)=card{j|(Xj,Sj)∈A}
(3)
其中,card{}表示集合中元素的个数。那么,由期望值定义的确定性测度
Λ(A)=E(N(A)),A∈C×B+
(4)
称为N的强度测度。
若Θ(t)表示随机闭集(Random closed set,RACS),表示在时间t∈R+之前,Ω中由晶相所占据的区域,即
(5)
其中:随机集Θ(t;Xj,Sj)表示在位置Xj和时刻Sj出生的晶体自由生长到时刻t≥Sj所占据的空间,
Θ(t;Xj,Sj)={x∈Ω:η∈C1[Sj,t],η(Sj)
=Xj,η(t)=x,
|η′(s)|≤ρ(η(s),s),s∈(Sj,t)}
(6)
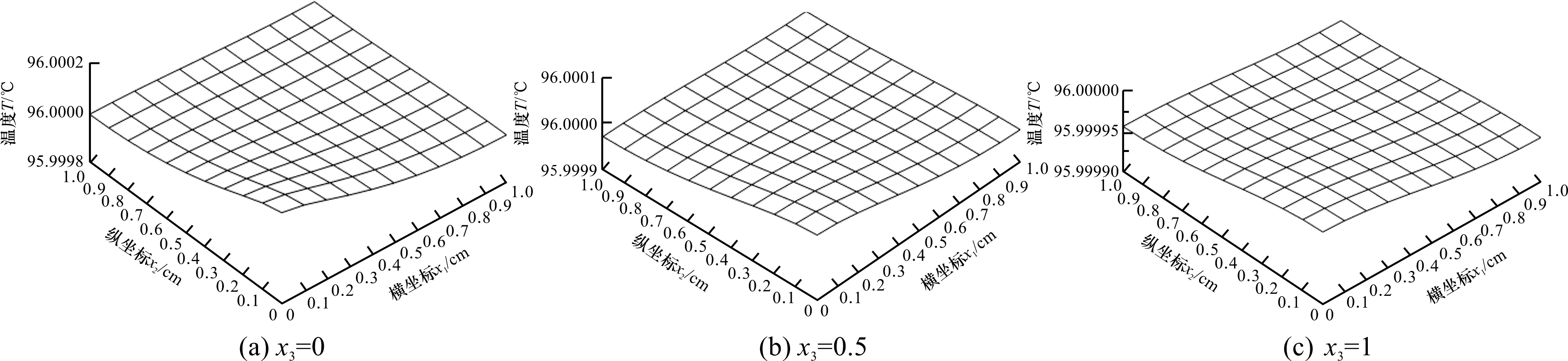
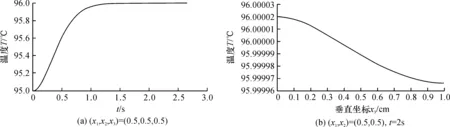
其中:ρ(x,t)表示生长率。当t 一般情况下,不直接使用集合Θ(t),而是定义一个便于计算的因果锥,即 E(x,t):={(y,s)∈Ω×[0,t]|x∈Θ(t,y,s)} (7) 或者 |y-x|≤ (8) 它是所有可能的成核事件(y,s)的集合,其中x将被结晶相Θ(t)占据。为了更好地理解因果锥的定义,下面针对空间二维情形给出具体的晶核生长速率的因果锥图。 图2 空间二维上不同生长速率的因果锥E(2,2,2) 在(x,t)∈Ω×R+中,单位体积和单位时间内晶核产生的平均数记为结晶度函数,即 ξ(x,t)=P(x∈Θ(t)),x∈Ω,t∈R+ (9) 那么,通过式(4)可以得到成核过程N的强度测度, Λ(dt×dx)=E(N(dt×dx)) =α(x,t)(1-ξ(x,t))dxdt 10) 从而,当x∈Ω时,单位体积内生成的晶核的平均数为 (11) 由泊松分布,可以得到 ξ(x,t)=1-e-γ0(E(x,t)) (12) 其中:γ0(E(x,t))是相对于泊松分布过程的强度测度的因果锥的体积,即 (13) 因此,ξ(x,t)依赖于成核率α(x,t)和生长速率ρ(x,t)。 通常情况下,成核过程释放的潜热会导致温度T(x,t)的变化,因此ξ(x,t)关于时间的导数将作为热扩散方程的源项: (14) 其中:c是热容,κ是热传导率,D是密度,q0是潜热系数。温度T(x,t)满足Robin边界条件 (15) T(x,0)=T0(x),x∈Ω (16) 由1.1和1.2可知,成核-晶核生长与热扩散过程耦合的偏微分方程模型为 (17) 本节对方程(17)进行数值仿真。通过给定的成核率α(x,t)和生长率ρ(x,t),得到空间三维区域内的温度分布T(x,t)。时间和空间上的区间分别是[0,S]和Ω=[0,l]3,方程(17)中的参数c,κ,D,q0,k0都是常数。 间步长h>0;tn=nΔt,(n=0,1,2,…,N),时间步长Δt>0。对于源项ξt(x,t)的离散处理,可以直接离散(需要先计算出ξ(x,t),再关于t求导),或者先对ξ(x,t)进行离散,即 (18) 当i,j,k=1,2,…,M-1时,定义差分算子 (19) 对方程(17)采用有限差分法进行离散得 (20) (21) (22) 利用式(20)—(22),可求得方程(17)的数值解。 图3 t=2 s时,不同截面的温度分布曲面 图4 不同位置点或不同时刻的温度分布曲线 由图3和图4可以看到,大概在2s时,温度不再发生变化,此时温度约为96 ℃,并且底层(x3=0时)的温度高于顶层(x3=1时)的温度。 通过上述介尺度模型(17)和反问题研究结果可以得到成核率α与晶核生长速率ρ,通过式(20)—(22)获得的数值模拟结果与化学实验结果对比,验证了模型(17)的合理性和数值算法(20)—(22)的有效性。 本文对铁系催化剂制备的稀浓度实验中Fe(OH)3晶核生成和长大的介尺度过程进行数学建模,建立了空间三维上的耦合抛物型方程模型,并借助数值算法和Matlab软件进行数值仿真。该数学模型及其数值算法研究,为稀浓度下Fe(OH)3的结晶过程提供了理论依据。 本文只给出了正问题的模型与计算,后续将研究相应反问题,如成核率决定反问题、生长率决定反问题或者两者同时决定反问题等。

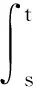



1.2 宏观尺度上的热扩散模型
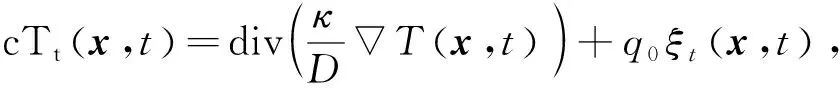


1.3 稀浓度下生成Fe(OH)3晶核的介尺度模型

2 耦合模型的数值算法

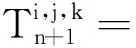

3 数值算例与结果分析
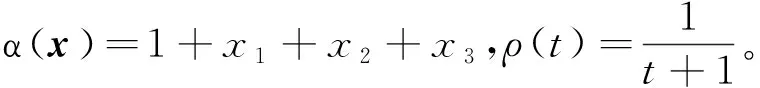
4 结 语

