宏观强度对水工原级配和湿筛混凝土拉伸断裂性能差异的影响

荆帅召，张 嘉，刘晓敏，徐 磊

(河海大学 水利水电学院， 江苏 南京 210098)

为了节省水泥用量和降低水化热，大体积水工混凝土通常采用最大骨料粒径达150 mm (或120 mm)的四级配骨料或者最大骨料粒径达80 mm的三级配骨料。开展原级配(三级配、四级配)混凝土力学性能试验需要制备尺寸较大的物理试件，对试验设备的要求较高[1-2]，故现阶段主要采用湿筛法来测试原级配混凝土的力学性能[3]。在湿筛前后，混凝土的骨料含量与级配将发生明显变化，因此通过湿筛法测定的力学指标与原级配混凝土的真实力学指标间存在差异[4]。

针对上述差异，已有学者开展了试验研究。陈文耀等[5]基于试验结果分析了原级配与湿筛混凝土抗拉、抗压强度差异的原因。唐天国等[6]分析了锦屏一级高拱坝混凝土原级配试验和湿筛试验强度测试的结果，发现大坝混凝土原级配试件28 d以上龄期的强度和变形均小于湿筛小骨料试件相应龄期的强度和变形。郑丹等[7]基于试验结果分析了混凝土在不同破坏模式下混凝土内控制性裂纹的长度，研究了最大骨料粒径对混凝土强度的影响规律。施林林等[8]研究三级配和湿筛混凝土的单轴动态受压性能，建立了二者强度、峰值应变、弹性模量和应变率的关系公式。现阶段，已有研究主要是采用物理试验手段开展，研究对象通常具有特定配合比，试件数量偏少，故成果缺乏系统性，且离散性较大。

作为物理试验方法的有力补充，细观有限元分析方法已在混凝土力学性能研究中得到广泛应用[9]。与物理试验手段相比，细观有限元分析不仅可通过均匀化方法获取混凝土的宏观力学参数，而且可揭示混凝土变形破坏的细观机制，并具有耗时少、费用低的特点，适于开展大样本统计分析。因此，本文采用细观有限元分析和Monte-Carlo模拟相结合的方法，研究在不同宏观强度下原级配和湿筛混凝土拉伸断裂性能的差异，揭示上述差异随宏观强度的变化规律及其致因。研究成果可为建立考虑宏观强度影响的原级配与湿筛混凝土拉伸断裂参数间的关系提供依据。

1 混凝土细观有限元计算模型

本文在细观尺度上将混凝土视为一种由粗骨料、砂浆(包括水泥基和细骨料)和界面过渡区构成的三相非均质复合材料。

为建立原级配和湿筛混凝土试件的细观有限元计算模型，需要依据给定的骨料级配和含量生成一组随机骨料并将其在一定约束条件下随机投放至具有特定尺寸的试件中，上述过程通常称为混凝土细观随机结构的生成，具体实现方法在文献[9]中已详细给出，不再赘述。文中针对水工原级配(三级配)及其湿筛混凝土开展研究，为与物理试验中采用的试件尺寸保持一致，原级配数值试件尺寸取为300 mm×300 mm，湿筛数值试件尺寸为150 mm×150 mm。此外，原级配混凝土平面内骨料含量取为50%，级配取为小骨料(5 mm～20 mm)：中骨料(20 mm～40 mm)：大骨料(40 mm～80 mm)=3∶3∶4，则湿筛混凝土骨料含量为37.5%，级配为小骨料∶中骨料=5∶5。图1为按上述要求随机生成的原级配及其湿筛混凝土试件细观结构(多边形代表粗骨料)。

图1细观结构

在上述基础上，尚需对生成的复杂混凝土细观结构进行网格剖分，为此本文基于通用有限元软件平台ABAQUS成熟的前处理模块，编制了可实现混凝土细观网格自动剖分的MATLAB程序[10]。图2给出了对图1所示细观结构进行自动剖分后所得的有限元网格，在网格剖分中，所编制的程序可实现在骨料与砂浆中自动插入一定厚度的界面过渡区，文中界面过渡区厚度取为100 μm[11]。

图2细观有限元网格

通过细观有限元分析模拟混凝土实际拉伸断裂过程，需赋予粗骨料、砂浆以及界面过渡区合理的本构模型及相应的力学参数。考虑到在拉伸断裂过程中，粗骨料通常保持完整，细观开裂破坏一般先出现于界面过渡区，后逐渐向砂浆中扩展[12]，故本文采用线弹性本构模型模拟粗骨料的力学行为，采用ABAQUS中的塑性损伤模型[13]模拟砂浆与界面过渡区的力学行为。由于界面过渡区的性能弱于砂浆，取界面过渡区力学参数为砂浆的75%[10]；另一方面，考虑到大骨料周围的界面过渡区与中、小骨料的界面过渡区相比存在更多缺陷，力学性能更弱，所以模拟中，粒径≥40 mm的大骨料周围的界面过渡区参数取为中、小骨料(5 mm≤粒径<40 mm)界面过渡区参数的0.8倍[14]。

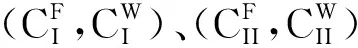
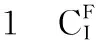
表细观力学参数

2 Monte-Carlo模拟

为取得具有统计意义的分析结果，在本文研究中运用Monte-Carlo随机试验方法，即对于节2中所述的任意一类原级配或湿筛混凝土，均建立一定数量(Nc)且具有不同细观结构的数值试件，以实现在差异分析中消除细观结构随机性的影响。

为了保证Monte-Carlo随机试验的统计收敛性，Nc需要足够大。为此，在分析中研究了各类混凝土宏观拉伸断裂性能指标的统计均值与样本(试件)数量之间的关系，发现当Nc取为30时，基本可实现统计收敛。因此，在本文研究中，共需开展180次(6×30次)细观有限元分析。

在细观有限元分析的基础上，尚需给出混凝土试件的宏观拉伸断裂性能指标(拉伸弹性模量Et、峰值拉伸应变εt、峰值抗拉强度ft以及断裂能Gf)。其中，ft定义为位移加载结点的结点反力之和的极值与试件边长的比值，εt为与ft相应的试件位移值与试件边长的比值，Et定义为εt与ft的比值，Gf可通过对应力-位移曲线积分进行计算。

3 结果分析

表2给出了不同宏观强度下原级配和湿筛混凝土宏观拉伸断裂指标的均值及其比值。从表2中可以看出，在不同的宏观强度下，原级配混凝土的拉伸弹性模量均大于湿筛混凝土的拉伸弹性模量，这主要可归因于原级配混凝土中粗骨料(抵抗变形能力强)含量高；随着宏观强度的提高，原级配与湿筛混凝土拉伸弹性模量的比值呈现出减小的变化趋势，其原因主要在于当骨料力学特性保持不变时，混凝土宏观强度的提高通常伴随着砂浆、界面过渡区抵抗变形能力的提高，而这将降低由于骨料含量减少所导致的湿筛混凝土拉伸弹性模量减小幅度。

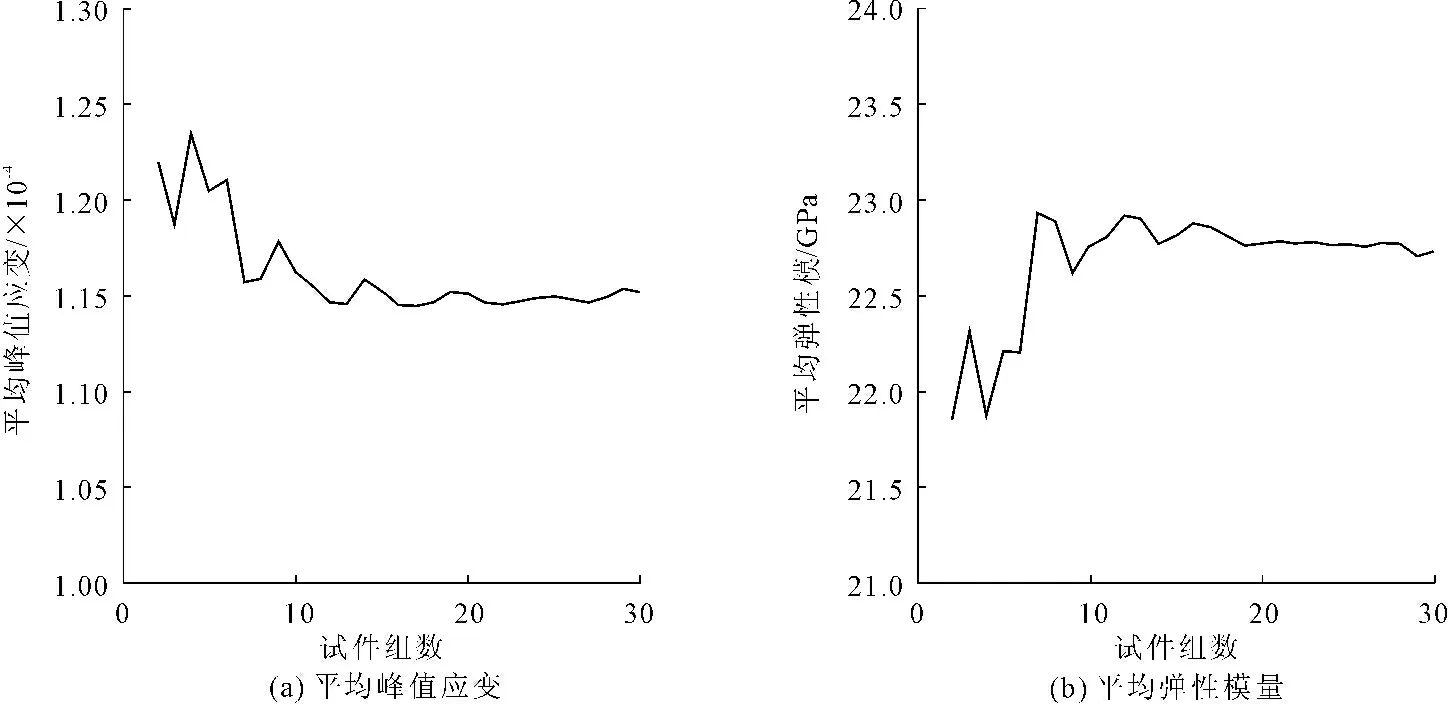
图3 宏观应力-应变曲线

图4统计均值与样本数量的关系曲线

在不同的宏观强度下，原级配混凝土的峰值抗拉强度均明显小于湿筛混凝土的峰值抗拉强度，这主要是由于原级配混凝土中大骨料周围存在力学性能更弱的界面过渡区；而随着宏观强度的提高，原级配与湿筛混凝土的峰值抗拉强度之比基本保持不变，且这一比值与大骨料与中、小骨料界面过渡区力学参数之比(0.8)接近，这表明相对于宏观强度，大骨料与中、小骨料周围界面过渡区的抗拉强度之比在更大程度上控制着原级配与湿筛混凝土峰值抗拉强度比值。

由于原级配混凝土的峰值抗拉强度小于湿筛混凝土，而拉伸弹性模量大于湿筛混凝土，故在不同的宏观强度下，原级配混凝土的峰值拉伸应变均明显小于湿筛混凝土；随着宏观强度的提高，由于峰值抗拉强度比值基本不变，而拉伸弹性模量比值逐渐降低，故原级配和湿筛混凝土峰值拉伸应变的比值呈现出逐渐增大的趋势。

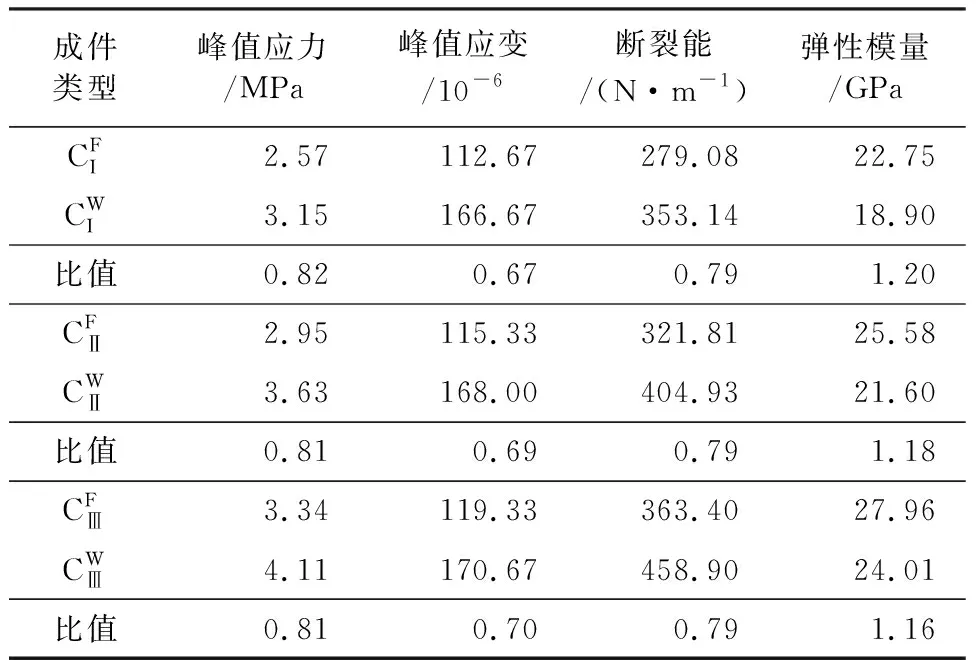
表2 宏观拉伸断裂指标的统计均值及其比值

在不同的宏观强度下，原级配混凝土的断裂能均明显低于湿筛混凝土的断裂能，其原因主要在于原级配混凝土中粗骨料含量高且大骨料周围的界面过渡区力学性能更为软弱；进一步可以发现，随着宏观强度的提高，原级配和湿筛混凝土的断裂能之比保持不变(0.79)，这一比值与大骨料与中、小骨料周围界面过渡区的断裂能比值(0.8)基本相同，这表明与峰值抗拉强度类似，原级配与湿筛混凝土断裂能的比值亦主要受控于大骨料与中、小骨料周围界面过渡区的断裂能之比。

4 结 论

(1) 在不同细观结构下，原级配和湿筛混凝土数值试件的软化阶段应力应变曲线存在明显的差异。

(2) 湿筛法对于原级配和湿筛混凝土的主要拉伸断裂性能指标有着不同影响，在不同的宏观强度下，原级配混凝土的拉伸弹性模量均大于湿筛混凝土，而原级配混凝土的峰值抗拉强度、峰值拉伸应变及断裂能则均小于湿筛混凝土。

(3) 随着宏观强度的提高，原级配和湿筛混凝土拉伸弹性模量的比值减小，峰值拉伸应变的比值增大，而峰值抗拉强度和断裂能的比值则基本保持不变(主要受控于大骨料与中、小骨料周围界面过渡区的抗拉强度与断裂能之比)。