浅析三峡水库泥沙运移特征

邹 敏，杨宏伟，徐 杨，陈胡兰

(1.长江水利委员会水文局长江上游水文水资源勘测局，重庆 400021；2.重庆三峡学院土木工程学院，重庆 404100)

三峡水库自建成蓄水以来，长江干流水深增加，最大深度可达200 m左右。水库对水流的拦截作用使得库区内的水流流速沿程减小，紊动扩散作用逐渐降低，又加之回水区域过长，从而导致库区河段内淤积了大量的泥沙。泥沙的大量淤积不仅会降低水库有效库容，抬高洪水位，改变水流特性，还会大大影响水库自身的综合效益，给长江中下游地区的人民带来安全隐患。水库清淤工作已经成为水利水电工程中的重中之重，在某种程度上来说，也是水利水电工程成败的关键。

关于泥沙输移规律认识多源于我国学者的理论研究、数据分析和实地考察。郭小虎等[1]根据三峡工程蓄水以来的实测资料对长江中游泥沙运移变化规律进行探讨，指出：自20世纪90年代三峡水库蓄水后，其年均含沙量逐年减少，截至2015年，减少至最低水平，含沙量大幅度减少将会引起长江中游长距离冲刷。毛红梅等[2]运用非线性回归技术，结合清溪场、万县站实测资料进行不同影响因素下悬移质泥沙横向分布和垂线分布的分析，得出泥沙横向分布较为均匀，而由于絮凝作用的影响，其垂线分布较为不均。陈建等[3]着重研究水沙条件变化对三峡水库泥沙淤积的影响，通过二维水沙模型计算得出：上游建库的综合作用相较于上游无库的情况将有效缓解三峡水库泥沙的淤积过程，部分河段会出现冲刷，航运条件会得到明显的改善。

虽然这些成果均较好地解释水库泥沙输移的一般规律，但并未形成定论，仍需进一步研究。本文基于三峡工程运用以来的实测资料，以三峡水库淤积泥沙为研究对象，借助水流泥沙数学模型方法，分析和探索库区内泥沙运移的规律。以期为长江中游江湖规划、治理以及江湖关系深入研究等提供理论支持。

1 水沙模型

建立水流泥沙数学模型，可以更有效地模拟河床冲淤量、河床形态及河床泥沙组成的变化、水流泥沙运动过程等物理模型无法模拟的方面。数值模拟作为研究水流泥沙运动重要的手段之一，在实际水利工程和理论分析中被广泛应用。

1.1 一维水沙模型

一维水沙数学模型通常用来计算在实际研究中遇见的大型水库的淤积、大坝下游坝踵处冲刷以及沿程冲刷和河口潮汐等方面的问题。一维水沙数学模型常用的基本方程有水流连续、运动方程，泥沙连续方程及河床变形方程。

水流连续方程：

(1)

(2)

水流运动方程：

(3)

(4)

(5)

泥沙连续方程：

(6)

(7)

河床变形方程：

(8)

(9)

(10)

式中：h为水深，m；u为流速，m/s；zb为河床高程，m；i0为床面坡降；if为摩阻能坡；g为重力加速度，m/s2；ρs、ρm、ρ为泥沙、清水及浑水密度，为床沙饱和密度和床沙干密度，kg/m3；s、s*分别为含沙量及挟沙力；α为恢复饱和系数；ω为泥沙沉速，m/s。

在此基础上，伍宁[4]运用圣维南方程组建立一维水沙数学模型，应用芙蓉江江口水文站、长江徐六径水文站实测水文资料进行分析验算，对解决非恒定流方面的一些实际的水文问题进行初步分析和探讨；廖康等[5]为寻找一维水沙模型中的重要参数“糙率”的计算方法，采用MIKE11一维水动力模型，对三峡库区重庆段一维水流模型“糙率”修正分析，实验证明该方法有效提高了模拟精度，降低“糙率”对模拟结果的影响，对我国在该方面的研究提供了理论依据；丁赟等[6]对现有一般水沙数学模型进行了特征分析，发现多数模型在特征上无法耦合的原因在于河床变形方程不能严格满足质量、动量守恒关系，为更好地解决这一问题，基于连续介质假设，推导得到了河床冲淤层质量和动量守恒方程，建立了特征耦合的水沙数学模型。

1.2 二维水沙模型

一维水沙数学模型在某种程度上存在局限性，即无法进行沿河宽方向和河深方面的模拟计算。因此，二维水沙模型应运而生。平面二维水沙数学模型在工程中被广泛运用于弯道冲淤变化、深潭和浅滩的演变、交错边滩的向下游运行和分汊河段主、支汊的交替发展等的分析过程。二维水沙数学模型常用的基本方程有水流连续、运动方程，泥沙连续方程及河床变形方程。

水流连续方程：

(11)

水流运动方程：

(12)

(13)

泥沙连续方程：

(14)

河床变形方程：

(15)

式中：z为水位，m；z0为河底高程，m，h为水深，m，h=z-z0；u、v为垂线平均流速沿x、y方向的分量，m/s；c为谢才系数，c=(1/n)h1/6；n为糙率系数；γt为紊动黏性系数；s、s*为平均含沙量及挟沙力；ω为泥沙沉速，m/s；c0为泥沙扩散系数；a为恢复饱和系数；γ′为泥沙干容重，kN/m3。

随着技术的不断改进和完善，二维水沙数学模型在水利工程中已有不少解决实际问题的成功先例。童思陈[7]通过研究典型水库淤积过程与运用方式的关系，分析了不同方案运用对水库纵向淤积推进、横断面淤积发展和兴利库容保留程度等的影响，并对水库泥沙数学模型的验证提出了建议；周兆杰等[8]采用特征有限元法来进行藕合求解，精确反映水流中泥沙的输移，研究结果有利于人们更加清楚地把握河道水流泥沙的形态，对于治沙、防治及堤坝的建设与加固都有积极而重要的意义；吴伟明[9]建立的平面二维水沙数学模型对河道水流、含沙量及河床的平面变形进行模拟，并利用葛洲1988—1991年4 a的水文泥沙实测资料对所建模型进行了验证，结果证明：该模型与实际的吻合度较高，可为工程应用决策提供理论依据。

1.3 三维水沙模型

由于自然界中普遍存在泥沙的对流、扩散、沉降、再悬浮、沿垂线方向不均匀分布等三维现象，所以要准确描述泥沙运动过程，三维水沙模型自然就成为了泥沙研究的新方向。

朱建荣[10]建立了三维非线性斜压浅海与陆架模式，以东海为研究对象，基于数值试验的方法成功研究了长江冲淡水扩展的机制。朱建荣基于ECOM-si，建立了三维高分辨率湍流闭合的黄海、东海海洋环流数值模式；刘高峰[11]在ECOM-si模型的水动力和盐度模块的基础上，建立了三维水沙输移模型，采用TVD格式来计算泥沙沉降过程，能更加精确的模拟泥沙沉降过程；马启南等[12]利用一个基于变换和内外模式分裂技术，建立了杭州湾的三维潮流数值模型。

2 推移质运动分析

2.1 定义

推移质是指以移动、跳跃、滚动的方式在河底运动的泥沙颗粒。推移质运动是泥沙输移的重要形式之一。推移质运动受到河床泥沙输送和起动的影响，而泥沙的起动与输送又受到河床结构的影响；而河床结构自身是在推移质运动过程中逐渐形成的，其结构形态和发育程度必然又受到推移质运动的影响。

2.2 研究现状

我国各地的研究人员通过对不同地区的实地勘探以及获得的大量数据，进行模拟实验，对推移质运动进行了全面深入的探讨和研究。张罗号等[13]基于在垂向条件下的瞬时紊动速度所得到的高斯分布规律，针对沙质河床，通过与实测材料的对比，建立了推移质颗粒级配曲线(见图1)。

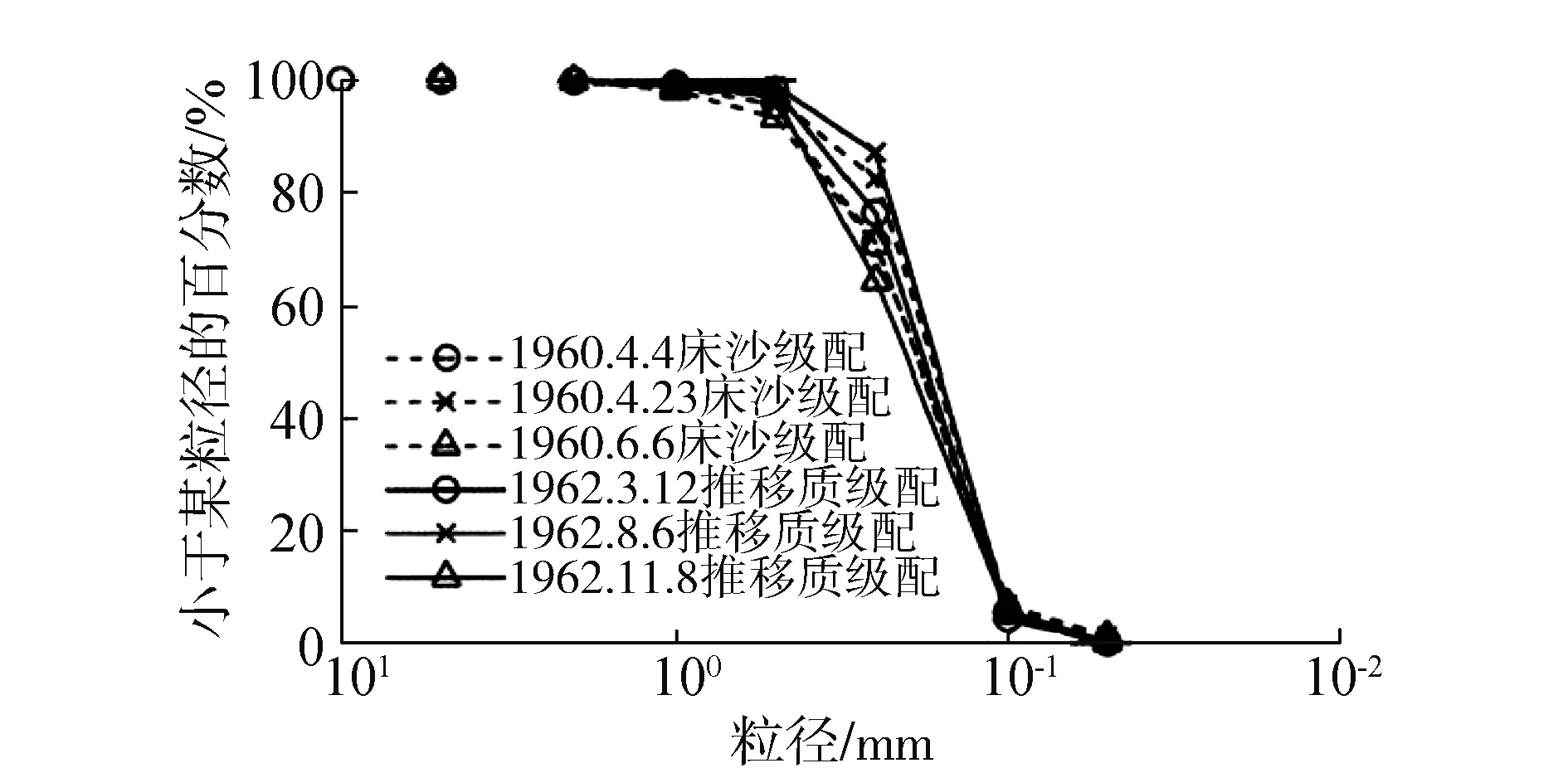
图1 推移质颗粒级配曲线

余国安等[14]以西南地区的山区河流为研究对象，研究了在不同的河床结构下推移质运动规律；提出推移质输沙率与河床结构发育程度系数，在一定前提条件下，两者成线性负相关关系。

王强等[15]通过研究河床形态、推移质运动与来沙条件之间的相互联系，得出：如果将已粗化河床细化，会导致冲刷效果加剧，使河床结构强度下降。不仅如此，加沙还会导致推移质范围扩大，加沙与河床级配之间的关系如图2所示。

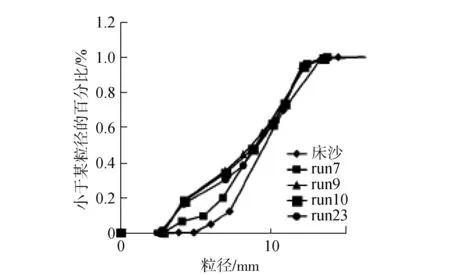
图2 各组试验的级配与原始河床级配曲线

推移质和床沙的中值粒径随时间的变化曲线如图3、图4所示。

图3 试验河床表面中值粒径随时间变化曲线

图4 试验推移质中值粒径随时间变化曲线

杨燕华等[16]针对坝下河段，基于典型水库坝下河段的相关实测资料，提出推移质在床沙百分数小于40%时为主要形式。

3 悬移质运动分析

3.1 定义

悬移质又称悬移载荷，悬移质运动是泥沙运动的主要形式之一。当河道发生冲刷时，部分较细颗粒的床沙被水流冲起，变成悬移质。悬移质泥沙浮于水中并随着运动，其运动轨迹也不规则。目前研究悬移质的理论主要有两种：扩散理论和重力理论。

3.2 研究现状

秦毅等[17]对处于冲淤平衡状态下的悬移质进行研究分析，在悬移质泥沙与床沙两者交换关系以及相关泥沙运动交换图形(见图5)的基础上，通过相应公式的计算，建立并验证了悬移质泥沙级配公式。

图5 悬沙与床沙交换模式

韩兴盛[18]采用的基本资料为民丰县境内代表站的悬移质泥沙实测资料，其中包括4个水文站的实测资料。基于尼雅水文站多年的悬移质泥沙数据，分析内容包括河流悬移质含沙量、输沙量。得到在地表径流出现高峰期期间，含沙量比较大；随季节差异，输沙量变化很大。

胡涛等[19]从悬移质含沙量分布方面，对目前的研究成果进行分析与检验。通过分析其他研究人员所提出的εxy常数的表达式，分析检验扩散理论，并依次分析重力理论、二相流理论以及湍流猝发理论、随机理论、混合理论，在所总结分析的理论支撑下，对典型含沙量分布公式(见式(16)～式(18))进行对比研究，并通过张小峰水槽资料对典型含沙量分布公式深入分析，得出各个典型分布公式。

(16)

(17)

(18)

式中：s为含沙量，kg/m3；sa为y=a处的饱和含沙量；k为卡曼常数，取0.4；h为水深，m；u*为摩阻流速，m/s；w为泥沙在静止水体中的沉速，m/s；ya为参考点高度，m；m0为大于1的系数，它与颗粒的尺寸、形状及含沙量的大小等因素有关。

吴凤元等[20]联合紊流以及悬沙运输两个方程得出单流体模型，运用有限体积法，用此模型对净冲刷、净淤积实验进行了数值模拟，并且可以使悬移质泥沙运动过程的数值分析更加合理有效。得出结果与实测结果大体一致，证明结论的有效性。

乐培九[21]在悬移质运动剖面的二维扩散方程的理论基础上，通过合理推测，最终收获饱和含沙量垂线分布的公式，并给出含沙量恢复饱和系数。

4 三峡水库对泥沙淤积的影响

三峡水库是世界上最大的水利工程，它的长期稳定运行对两岸经济发展以及社会和谐发挥着巨大的作用。它给我们生活带来便利的同时，也随之产生了一系列亟待解决的问题，其中最为急迫的就是库区泥沙淤积问题。

据相关数据统计，自建坝蓄水以来水库淤积下来的流域年产沙量达到5.3亿t，在2003年6月—2013年6月10 a期间，三峡入库悬移质泥沙总量为4.969亿t，总体输沙量减少趋势明显。不考虑三峡库区区间来沙，水库淤积量已达15.31亿t，年平均淤积量约为1.39亿t。由于库区水位的上升，导致水流的挟沙能力较小，含沙量处于超饱和状态，尤其是常年回水区(涪陵至三峡大坝)的泥沙淤积量最为显著，淤积量为14.090亿t，占总淤积量的92%左右。

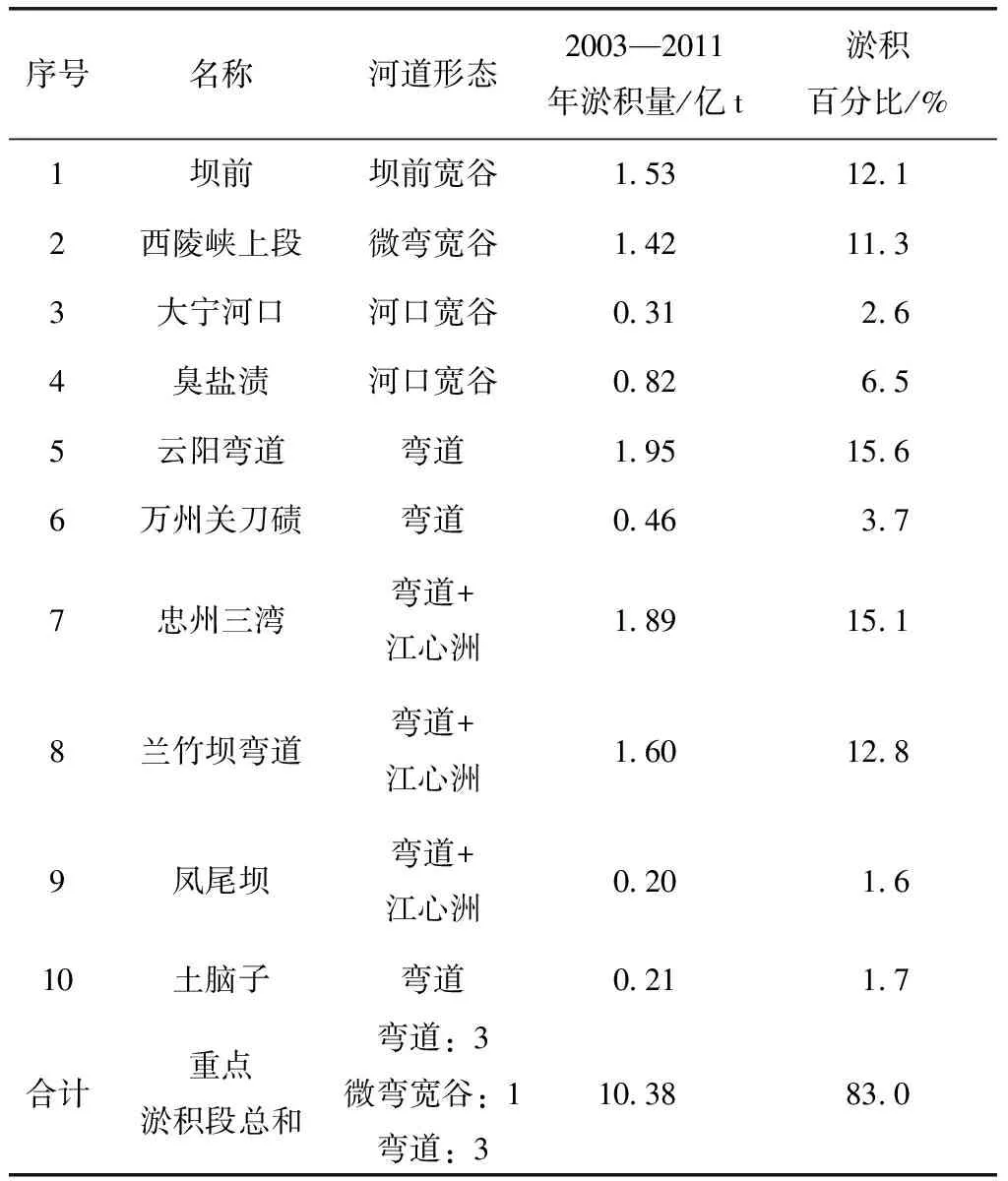
表1 三峡水库各重点淤积区淤积量(2003—2011年)

其中2013年，三峡入库悬移质输沙量为1.270亿t，出库(黄陵庙站)悬移质泥沙0.328亿t，库区淤积泥沙0.942亿t，水库排沙比为25.8%。

由表1可知，随着三峡水库蓄水后水位的上升，库区内的泥沙淤积量逐年增加，再加之三峡库区河道呈现宽窄相间、岸线参差不齐、浅滩和深槽高程变化明显、冲刷淤积交替等特点，最终使得库区内泥沙呈现宽谷淤积而峡谷不淤的不连续性淤积状态。

水库的泥沙淤积量还跟汛期时间有着很大的关系。付旺彬[22]指出三峡水库泥沙淤积主要发生在汛期(5—10月)，其中以主汛期(7—9月)的泥沙淤积最为显著，来沙约占全年的70%～90%左右。汛期三峡水库各重点淤积区淤积量见表2。

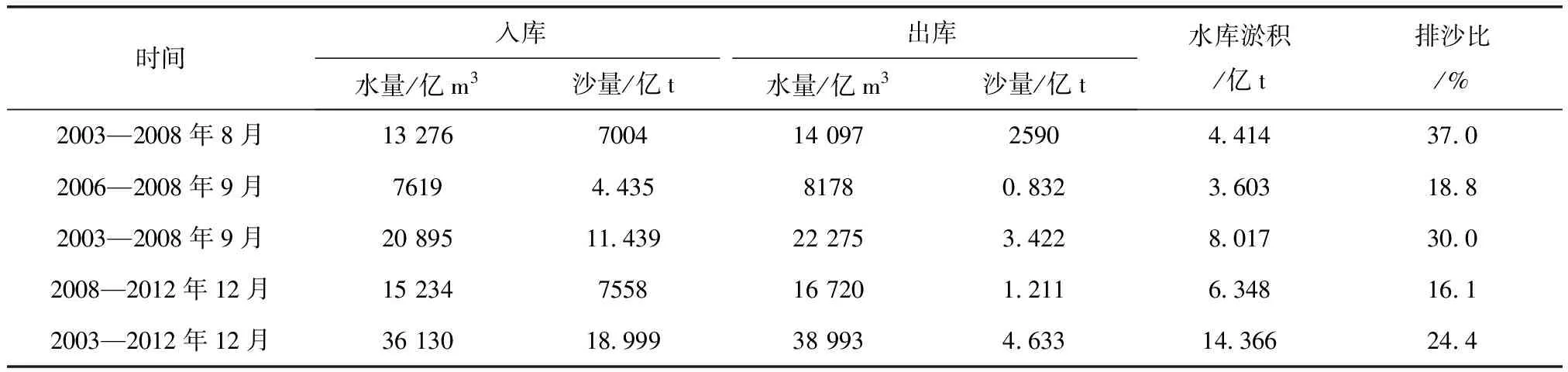
表2 三峡水库进出库泥沙与水库淤积量

5 结 论

自2003年三峡水库建成蓄水以来，三峡水库(主要针对常年回水区)淤积泥沙运移主要呈现以下几个显著特点。

(1)河道的形态对泥沙冲淤分布起着重要作用，常年回水区呈现宽谷淤积而峡谷不淤的不连续性淤积状态。

(2)泥沙淤积主要发生在每年汛期(5—10月)，其中以主汛期(7—9月)淤积最为明显，表现出的冲淤规律为“汛淤枯冲”。

(3)由于库区内蓄水位升高，水流的挟沙能力显著降低，导致水动力条件进一步减弱，从而引起各粒径组泥沙淤积更为显著。

(4)淤沙主要存在常年回水区，即涪陵至三峡大坝水段，变动回水区相对较少。

(5)库区水体在大水深、小含沙量情况下，泥沙横向分布趋于均匀，垂向底部区域泥沙输移占比较大。

(6)库区淤积物以中值粒径D50<0.062 mm的泥沙为主。