基于改进时延估计的声源定位算法

程方晓, 刘 璐, 姚清华, 韩 笑, 宋 曦

(1. 长春工业大学 电气与电子工程学院, 长春 130012； 2. 国家电网公司信息通信分公司, 北京 100761； 3. 夏威夷大学 土木与环境工程学院, 美国 夏威夷州 火奴鲁鲁 96816)

语音通信是信息交互中最有效的方法之一. 随着人机交互、 机器学习和模式识别等人工智能技术的飞速发展, 人工智能语音交互技术得到广泛关注[1]. 基于麦克风阵列的声源定位问题可等效于宽带短时平稳信号的空间谱估计问题, 其不仅可用于语音处理领域, 还可借鉴到其他超宽带信号处理领域, 如无线通信、 雷达等领域, 实现高精度定位, 是目前阵列信号处理的研究热点[2].

在无噪声、 无混响、 距离声源很近的情况下, 由单个麦克风构成的系统可获得高质量的语音信号, 但其拾音范围有限, 若声源在麦克风的选择方向外, 会引入大量噪声[3]. 相比于单一麦克风, 麦克风阵列具有较大优势, 可弥补单麦克风在噪声处理、 声源定位跟踪和语音分离等方面的不足, 因此广泛应用于具有嘈杂背景的语音通信环境, 如智能机器人、 视频会议系统、 助听器和车载免提电话等[4].

传统的声源定位方法可分为3类： 基于波束形成[5]的方法, 基于高分辨率谱估计[6]的方法和基于到达时间差(TDOA)[7]的方法, 它们分别将声源与阵列结构的关系转换为空间波束、 空间谱或到达时间差等信息, 并通对这些信息的估计进行声源定位. 其中, 基于时延估计的方法计算复杂度较低、 实时性好且硬件成本低, 可广泛用于声源定位与目标跟踪[8]. 本文在综合分析广义互相关算法和LMS(最小均方)自适应滤波算法的基础上, 提出一种基于改进时延估计的声源定位算法, 并进行了实验分析. 实验结果表明, 与相位变换加权广义互相关函数(GCC-PHAT)算法相比, 该算法具有更好的抗噪和抗混响的鲁棒性, 能获得更准确的定位结果.

1 阵列信号接收模型

图1 单源多元混响模型Fig.1 Single source multiple reverberation model

在实际环境中, 由于环境噪声和信号传播过程中的多径效应的影响, 环境噪声、 混响和语音信号将同时辐射在阵列平面上, 此时, 麦克风阵列的接收信号模型如图1所示. 该模型等效于一个单输入多输出系统, 由于环境噪声和混响的作用, 麦克风接收到的信号不再是简单的语音信号, 而是多个信号源的延迟与噪声信号的叠加[9].

设声源信号为s(n), 声源到第i个麦克风的信道冲激响应为hi(n), 噪声信号为vi(n), 此时, 第i个麦克风接收到的信号为

xi(n)=hi(n)s(n-τi)+vi(n)=αis(n-τi)+

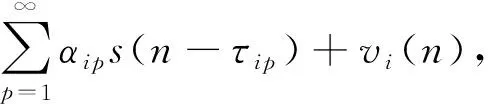
(1)

其中系数αip和τip分别表示信号经过反射路径p到达麦克风i的衰减和时延. 由于声音直接到达麦克风的路径最短, 所以τip>τi. 此外, 经多次反射后, 信号的幅度会减小, 满足αip<αi. 实际上,αip以τip的指数形式衰减, 即信号的幅度随反射次数的增加衰减较快.

当室内无混响存在时, 阵元Mi和Mj接收到的信号xi(n)和xj(n)分别为

当室内存在混响时, 两阵元接收到的信号分别为

2 时延估计算法

2.1 广义互相关时延估计算法

广义互相关(generalized cross correlation, GCC)算法是目前应用最广泛的一种时间估计方法[10]. 由于同一声源发出的信号之间存在一定的相关性, 因此, 可通过计算不同麦克风接收到的信号间的相关函数估计TDOA值. 但在实际环境中, 由于噪声和混响的作用, 相关函数的最大峰值会被减弱, 有时还会出现多个峰值, 导致检测实际峰值变得十分困难. 广义互相关函数Rij(τ)定义为

(6)

其中：Gij(f)表示信号的互功率谱;φij(f)表示频域上的加权函数. 广义互相关函数算法的流程如图2所示. GCC方法在功率谱域对信号进行加权, 突出相关的信号部分而抑制受噪声干扰部分, 使相关函数在时延处的峰值更突出.

图2 广义互相关算法实现框图Fig.2 Block diagram of implementation of generalized cross-correlation algorithm

由图2可见, GCC方法是建立在非混响模型基础上的. 由于模型误差的影响, 其不能正确识别多个说话人和方向性的干扰噪声, 且更倾向于估计强信号的TDOA值, 因此, GCC方法通常用于低混响和非相关噪声的情况. 但低计算复杂度及易于实现的特点使GCC方法仍得到广泛应用.

2.2 LMS自适应滤波算法

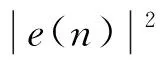
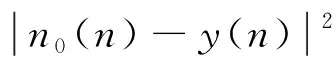
(7)

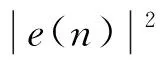
2.3 二次相关法

二次相关法先分别对两路信号进行自相关和互相关运算, 然后通过对得到的自相关和互相关函数进行相关运算, 以提高信号的信噪比与分辨力[12]. 二次相关法的原理如图4所示.

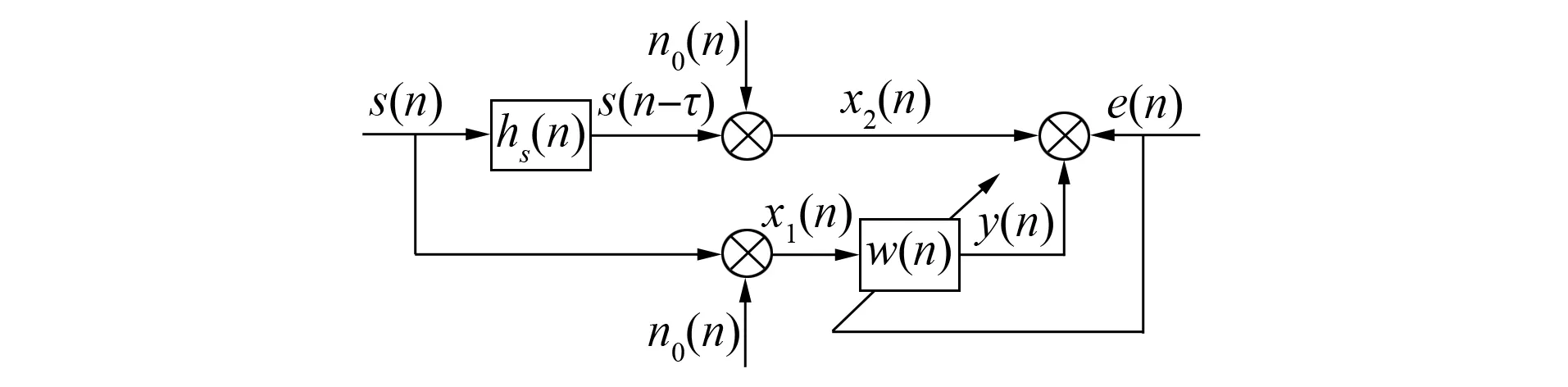
图3 LMS自适应滤波算法原理框图Fig.3 Block diagram of principle of LMS adaptive filtering algorithm

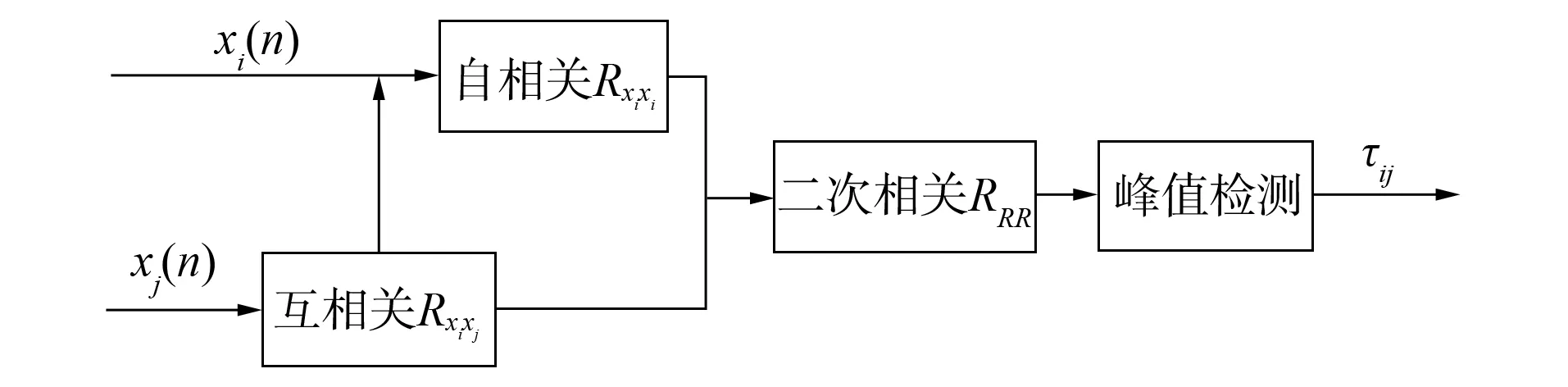
图4 二次相关法Fig.4 Quadratic correlation method

分别对信号xi(n)和xj(n)做自相关与互相关运算, 即

由式(8),(9)可知,x(n)的自相关函数Rx1x1(τ)与两路信号的互相关函数Rx1x2(τ)仍是时间的函数, 将其视为一个新的信号和噪声, 再对其做相关运算, 得到二次相关函数为

忽略信号与噪声的互相关函数, 则式(10)可简化为

RRR(τ)=λRss(τ-D)+Rn1n2(τ),

(11)

2.4 改进时延估计算法

利用广义互相关法与二次相关法可在一定程度上降低噪声对时延估计的影响, 提高估计精度, 但也有其局限性. 广义互相关利用权重函数增加信号中有效频谱的权重, 从而提高时延估计的精度, 但在低信噪比环境下的性能急剧下降； 而二次相关时延估计法利用相关函数抑制噪声干扰, 提高了时延估计算法的抗噪性能, 但其估计精度有待提高. 本文在GCC的基础上, 首先利用自适应滤波器对信号和噪声的先验知识需求较少、 具有自动调节参数的能力, 对声源信号进行滤波处理, 再通过引入二次相关法对广义互相关时延估计算法进行改进, 以提高算法的抗噪声和抗混响能力.图5为改进算法的原理框图.

图5 改进的时延估计算法Fig.5 Improved time delay estimation algorithm

3 空间定位方法

目前采用两种方法估计声源的位置： 通过搜索[13]的方式和通过几何方法[14]采用次最优的方式. 直线型麦克风阵列可对平面上的声源进行定位, 但在实际应用中更多需要给出声源的三维空间信息, 而直线型麦克风阵列显然不能满足要求. 因此, 本文采用平面麦克风阵列结构估计声源位置.

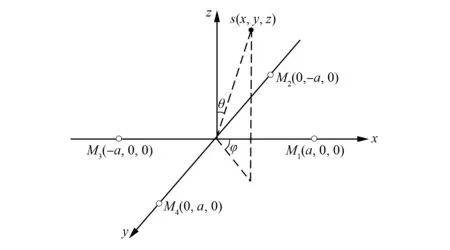
图6 四元十字阵列空间定位Fig.6 Spatial orientation of quaternary cross array

图6为四元十字阵列空间定位原理图. 该阵列是由4个麦克风组成的四元十字型麦克风阵列, 具有结构小巧、 便于安装在仿真智能机器人头部等优点. 阵列呈十字型结构对称分布在x轴和y轴上, 采集同一声源信号. 先估计各麦克风之间的延迟差, 再利用几何关系计算声源的空间位置. 由图6可见, 麦克风M1～M4的坐标分别为M1(a,0,0),M2(0,-a,0),M3(-a,0,0),M4(0,a,0), 声源信号的坐标为s(x,y,z), 声源s与坐标原点的距离用R表示； 声源s与x轴正方向的夹角, 即方位角用φ表示； 声源s与z轴正方向的夹角, 即俯仰角用θ表示.

假设分别用ri(i=1,2,3,4)表示声源到麦克风的距离, 用ti(i=1,2,3,4)表示声源到达麦克风的时间, 用τij(i,j=1,2,3,4)表示声源到达麦克风Mi与Mj之间的时间延迟. 假设声源位于远场, 则近似求得目标声源的位置表达式为

(12)

在多数四元十字阵列的空间定位方法中, 通常使用1个麦克风与其他麦克风的时延差值进行定位计算, 使用的时延差值信息不全面. 为进一步提高该空间定位方法的准确性, 本文以4个麦克风M1～M4分别作为参考麦克风, 先分别计算参考麦克风与其他麦克风之间的时延差值, 然后对获得的4组数据中相应的时延差值对进行加权平均运算, 将得到的平均值作为最终的时延值用于定位估计. 虽然运算量有所增加, 但定位结果的准确性得到了有效提高, 且仍能满足系统的实时性要求.

4 仿真实验

本文所有实验均在一个长12.8 m、 宽10.5 m、 高3.5 m的室内环境中完成, 已知房间内存在一定背景噪声与混响, 包括电脑主机风扇的声音和其他人为干扰等, 声源为实验环境中提前录制的一段语音. 本文以GCC-PHAT算法作为参考, 通过仿真实验比较改进算法与GCC-PHAT算法的性能优劣. 通过引入3个参数描述算法的定位精度, 包括归一化投影误差、 均方根误差和异常点百分数.

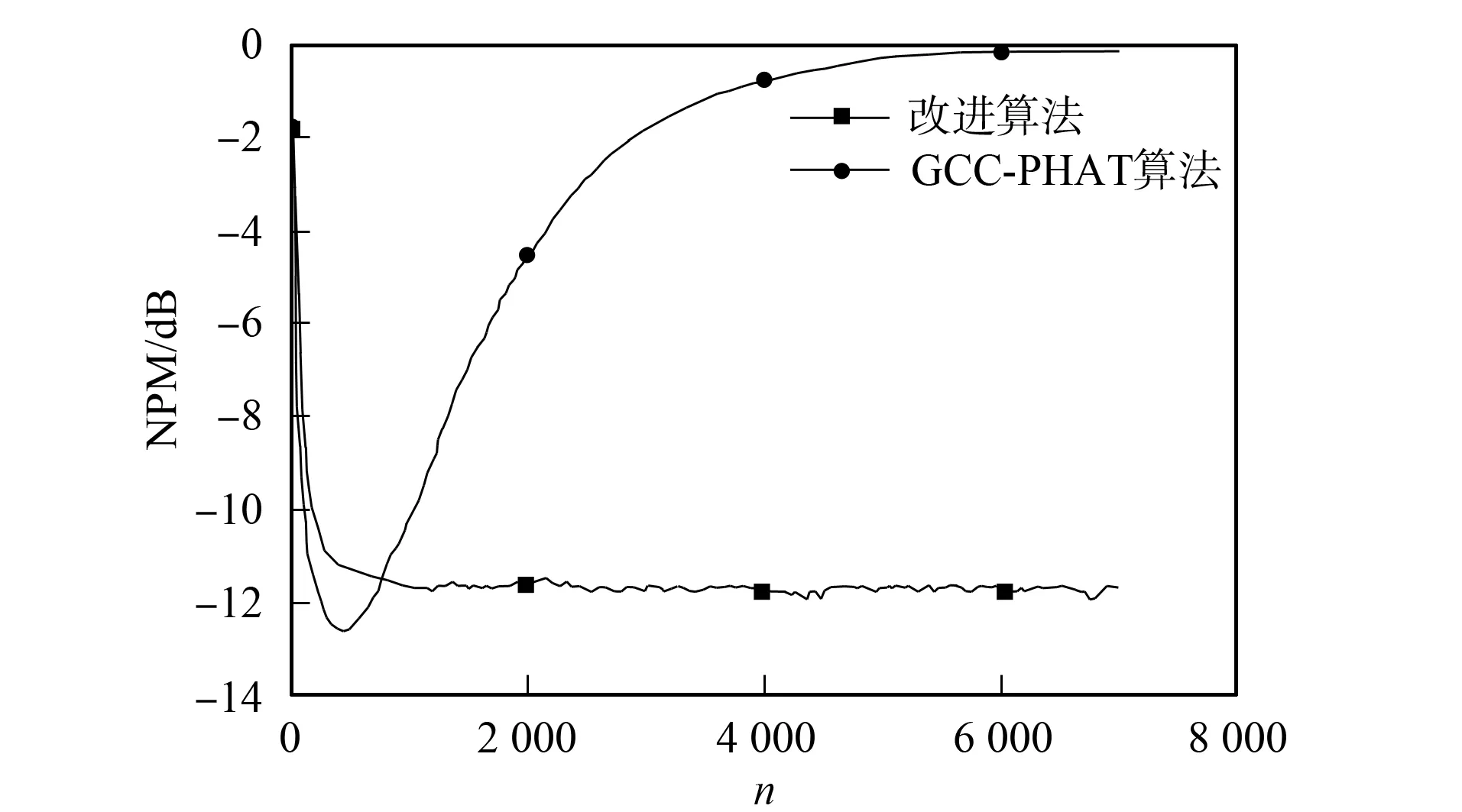
图7 两种算法的收敛曲线Fig.7 Convergence curves of two algorithms

4.1 抗噪效果分析

将归一化投影误差(normalized projection misalignment, NPM)作为算法抗噪性能的评价指标. NPM越小, 则抗噪能力越强. 在信噪比SNR为20 dB, 混响时间为100 ms的环境下进行仿真实验,图7为改进算法与GCC-PHAT算法的收敛曲线对比结果. 由图7可见, GCC-PHAT算法很快就发散, 收敛性较差； 而改进的时延估计算法可快速地收敛, 能有效避免由噪声引起的信道估计恶化问题, 具有较好的抗噪能力.

4.2 抗混响效果分析

用异常点百分数(percentage of abnormal point, PAP)衡量时延估计过程中出现异常点的可能性, 用均方根误差(root mean square error, RMSE)反映时延估计的精度, 其值越小, 表明时延估计值越接近真实值. 当时延估计值与真实值相差2个或2个以上抽样点时, 假设该估计值为一个异常点[15]. 异常点百分数定义为

(13)

(14)

其中:τ0表示真实的时延值；τi表示第i个时延的估计值;Nτ表示时延估计总数.

在实验中, 将声源分别放置在不同位置, 在信噪比SNR=20 dB保持不变, 而混响时间RT60处于变化的环境下, 对本文提出的改进算法与GCC-PHAT算法分别进行性能测试, 仿真结果如图8所示.

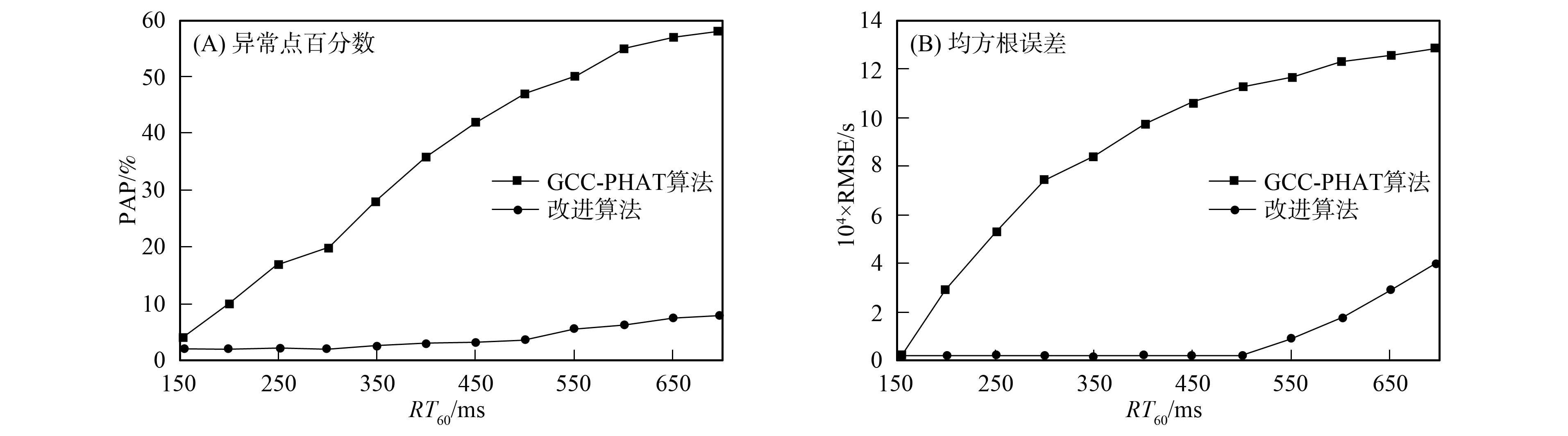
图8 两种算法的PAP和RMSE比较Fig.8 Comparison of PAP and RMSE of two algorithms

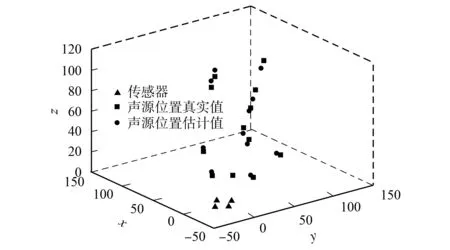
图9 定位仿真实验Fig.9 Positioning simulation experiment

由图8可见, 在低混响环境下, 两种算法均表现出良好的性能, 当混响时间大于300 ms时, GCC-PHAT算法的PAP明显增加, 其均方根误差远大于信号的采样精度, 无法进行有效地时延估计； 而在较强混响的环境下, 本文提出的改进算法仍能得到有效地时延估计, 因此, 与GCC-PHAT算法相比, 改进算法具有更强的抗噪能力, 更适合室内混响环境.

4.3 实验结果与分析

采用改进的时延估计算法, 并结合十字型麦克风阵列结构进行仿真实验. 设置系统的采样频率为50 kHz, 阵元间距为20 cm, 声源距离为100～250 cm. 分别选取8个声源位置, 对优化前后的时延估计算法进行实验, 在每个声源位置分别采集30组数据,图9为定位仿真实验结果, 得到的数据列于表1.

表1 算法优化前后定位误差

由表1可见, 算法改进后系统的定位误差明显下降. GCC-PHAT算法的方位角误差最大值达14.6°, 最小值达7.1°, 算法改进后方位角误差最大值为12.2°, 最小值为3.7°； GCC-PHAT算法的俯仰角误差最大值达16.8°, 最小值达8.2°, 算法改进后俯仰角误差最大值为12.3°, 最小值为3.9°； GCC-PHAT算法的距离误差最大值达23.2 cm, 最小值达12.8 cm, 算法改进后距离误差最大值为20.4 cm, 最小值为9.5 cm.

综上所述, 本文在建立阵列信号接收模型的基础上, 提出了一种基于改进时延估计的声源定位算法. 该算法首先对声源信号进行滤波处理； 然后进行二次相关运算, 有效地抑制了噪声干扰, 提高了系统的抗噪性能； 最后对二次相关的结果进行广义互相关加权处理, 进一步去除噪声, 以提高信号的信噪比, 从而提高时延估计的精度. 实验结果表明, 与GCC-PHAT算法相比, 该算法具有较好的抗噪与抗混响能力, 有一定的实际应用价值.