求解一类介质散射问题的特殊解方法

栾 天, 李双双, 张 威

(北华大学 数学与统计学院, 吉林 吉林 132013)

1 数学模型

考虑时谐波被有界可穿透障碍物的散射问题[1-2], 其对应的数学模型为如下带有辐射条件的Helmholtz方程定解问题:

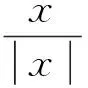
本文提出一种特殊解方法, 利用基本解函数逼近场的性态, 无需将无界区域截断, 从而避免了人工边界带来的数值误差, 且数值实现过程简单. 目前, 类似的方法有超弱变分方法(UWVF)[3-4]、 平面波间断Galerkin方法(PWDG)[5]和间断加强法(DEM)[6]等, 这些方法已被用于障碍散射问题[7]、 光栅衍射问题[8-9]、 近场散射问题[10-11]、 开腔体散射问题[12]和一些工程问题[13]等的数值计算.

2 数值算法

首先, 分别定义单层位势函数和双层位势函数如下：

其中:

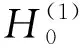
其次, 给出散射解的有限维近似空间.

us(x)=(Dli-ikiSli)ψi,x∈Di.

(4)

在闭曲线li上选取有限个离散点yij(j=1,2,…,Pi,Pi∈), 则由式(4), 散射场可近似为

这里cij∈为待求系数. 于是,Di上散射解的有限维近似空间Vi(i=1,2,…,N)定义为

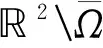
(6)

在闭曲线γi上选取有限个离散点zij(j=1,2,…,Qi,Qi∈), 则由式(6), 散射场可近似为

这里cij∈为待求系数. 于是,上全场解的有限维近似空间V0定义为

综上, 散射解的有限维近似空间可定义为

V={v:v|Di∈Vi,i=0,1,2,…,N}.

最后, 通过数值方法使散射场在Γ处近似地满足连续性条件. 利用解及其法向导在Γ处的跃度可定义目标泛函如下:

(8)

其中:

‖·‖0,Γi表示Γi上的L2范数; [·]表示函数f在Γi处的跃度, 定义为

νi为Γi上的单位外法向量. 若记式(8)的解为

(9)

则uN即为所求问题中全场的数值解.

3 数值实验

下面利用MATLAB软件通过3个算例对本文算法进行数值模拟, 验证其有效性.

例1散射体Ω为六叶草形状, 其边界曲线Γ的极坐标方程如下:

Γ(δ)=0.8+0.08cos(6δ), 0≤δ≤2π.

l(t)=1+0.1cos(6t), 0≤t≤2π;

在闭曲线l上选取有限个离散点yj(j=1,2,…,Q,Q∈). 在区域Ω内选取闭曲线γ, 其极坐标方程为

γ(δ)=0.64+0.064cos(6δ), 0≤δ≤2π;

在其上选取离散点zj(j=1,2,…,P,P∈). 为简单, 取P=p,Q=2p,p∈. 于是

图1 例1的散射体Fig.1 Scatterer of example 1

分别如图1中最外圈圆点和最内圈圆点所示.

最后, 考察算法的收敛性. 通过逐步增加p, 分别计算对应的泛函值J(uN)1/2, 数值结果如图4所示. 由图4可见, 随着p的增加, 泛函值J(uN)1/2逐渐减少. 当p=130时, 精度已达10-6, 表明收敛速度较快.

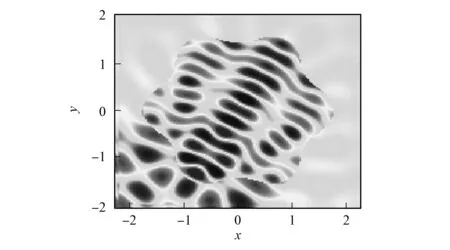
图2 例1的散射场us实部Fig.2 Real part of scattered field us of example 1

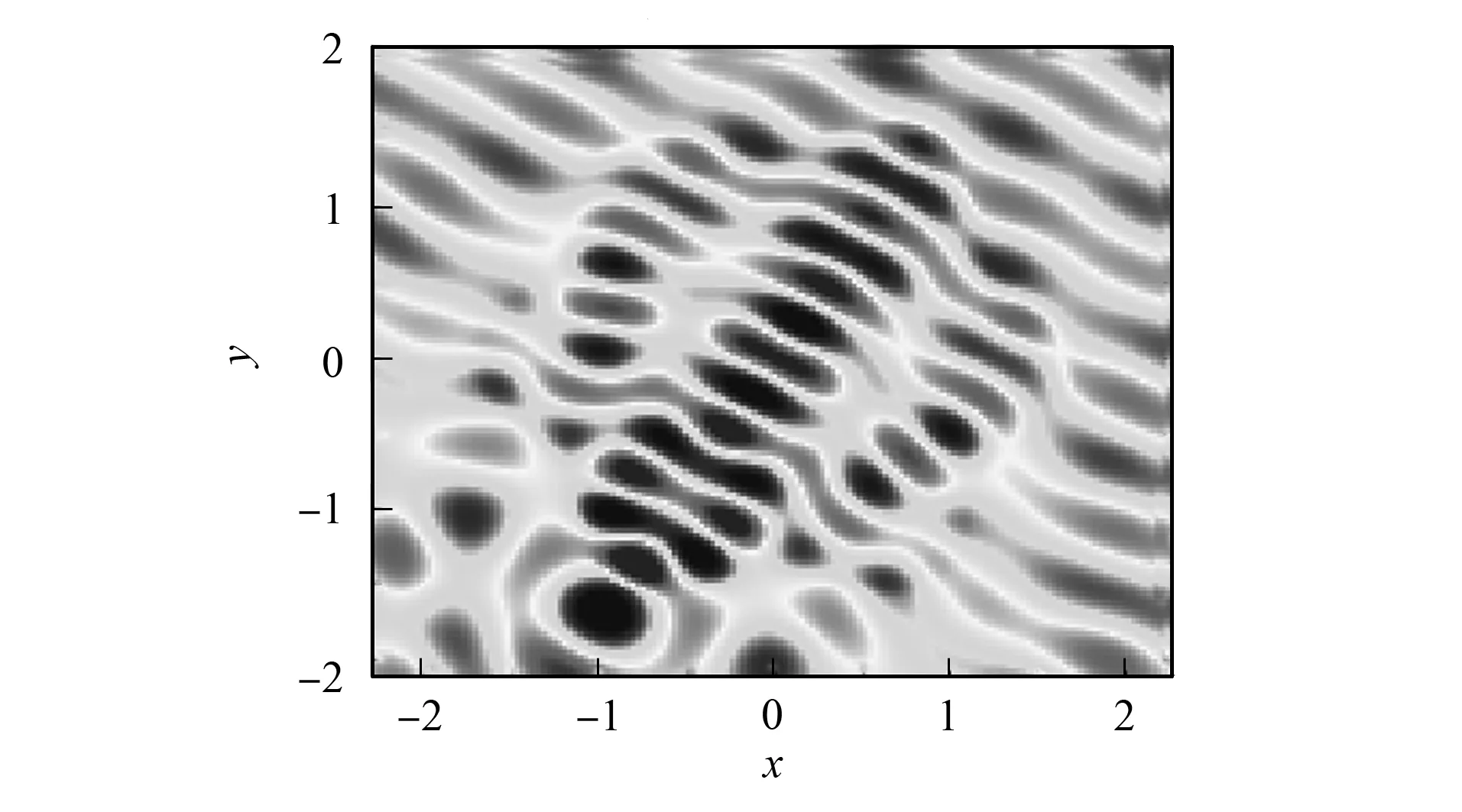
图3 例1的全场u实部Fig.3 Real part of total field u of example 1

例2设散射体D1和D2为具有不同波数的两个圆, 其边界曲线的参数方程分别为

数值模拟过程与例1相同. 首先分别在D1与D2外的闭曲线

上选取离散点y1j(j=1,2,…,P1,P1∈)和y2j(j=1,2,…,P2,P2∈). 在D1与D2内的闭曲线

上选取离散点z1j(j=1,2,…,Q1,Q1∈)和z2j(j=1,2,…,Q2,Q2∈). 为简单, 取P1=P2=p,Q1=Q2=2p,p∈. 于是

分别如图5中最外圈圆点和最内圈圆点所示.

图4 例1的数值收敛结果 Fig.4 Numerical convergence results of example 1

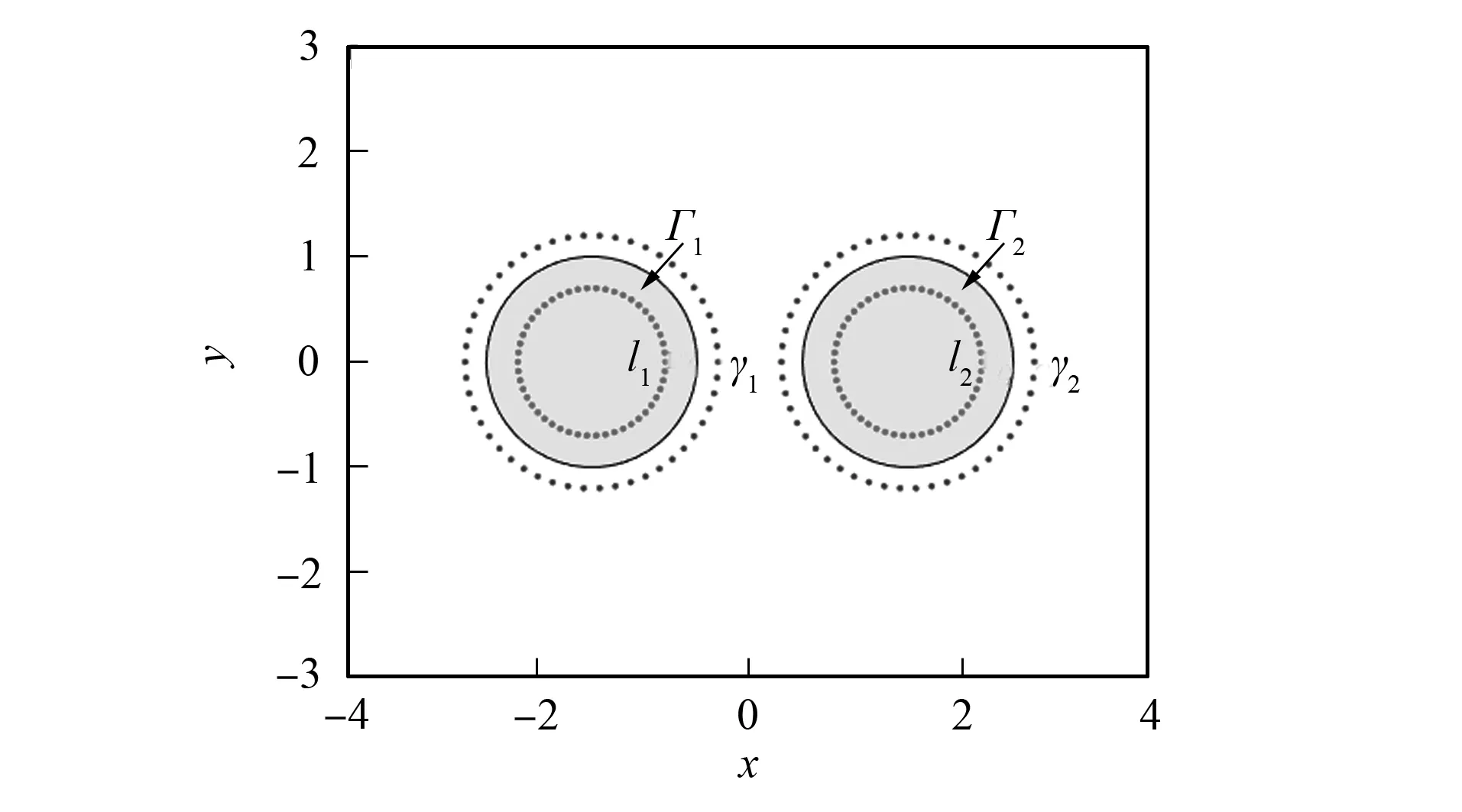
图5 例2的散射体Fig.5 Scatterer of example 2

其次, 取入射角θ=0, 波数k0=10,k1=15,k2=30,p=100, 分别计算入射场散射场us和全场u, 结果分别如图6和图7所示.

最后, 逐渐增加p值, 分别计算对应的泛函值J(uN)1/2, 结果如图8所示. 由图8可见,J(uN)1/2随p的增加快速衰减.

例3散射体为带有圆形孔洞的六边形区域, 其边界曲线的参数方程分别为

Γ1(t)=((1+0.1cos(6t))cost,(1+0.1cos(6t))sint), 0≤t≤2π;

Γ2(t)=(0.4cost,0.4sint), 0≤t≤2π.

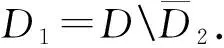
上选取如图9中最外圈和最内圈圆点所示的离散点

和

在D1内的闭曲线

l3(t)=(0.48cost,0.48sint), 0≤t≤2π

上选取如图9中第四圈圆点所示的离散点

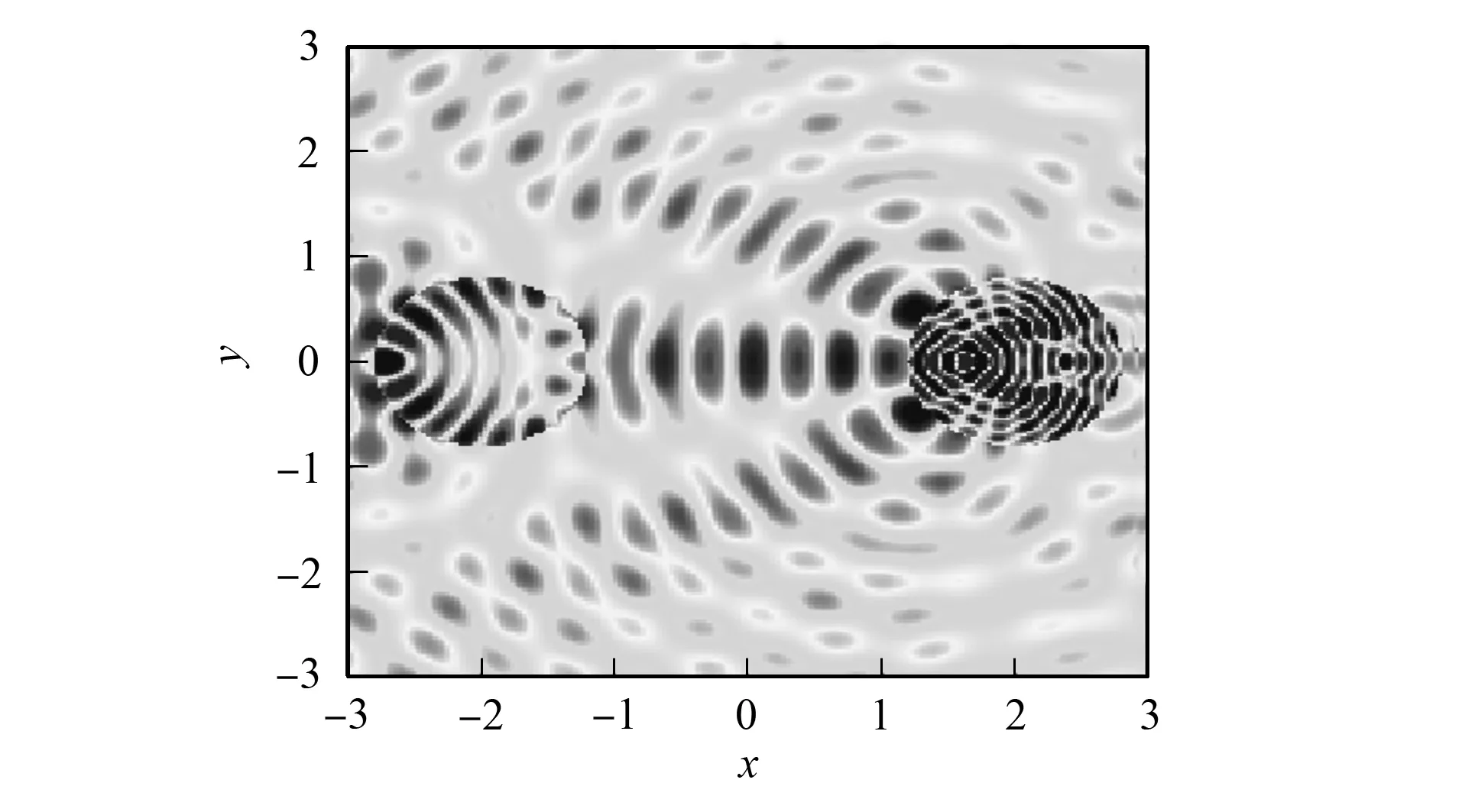
图6 例2的散射场us实部Fig.6 Real part of scattered field us of example 2

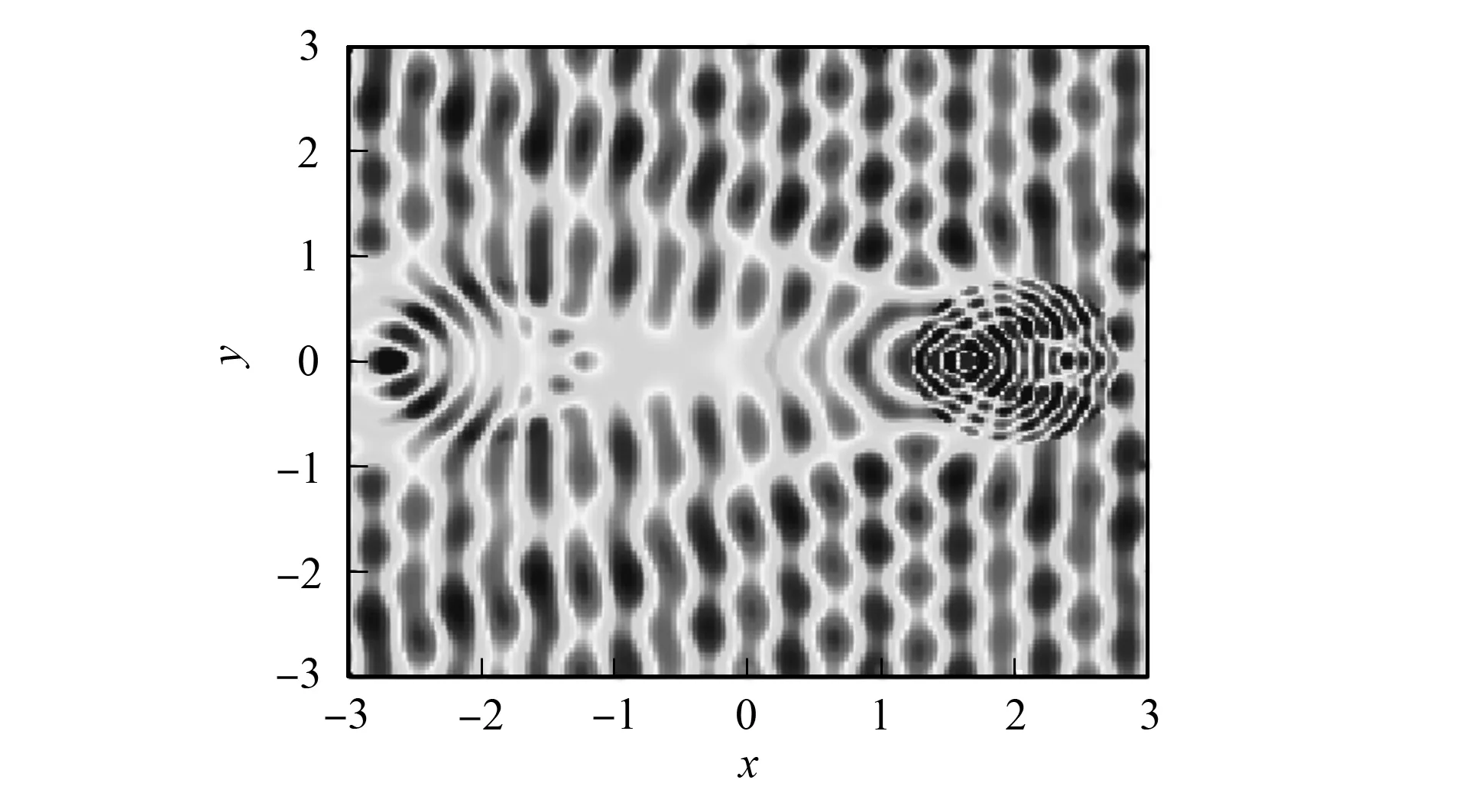
图7 例2的全场u实部Fig.7 Real part of total field u of example 2

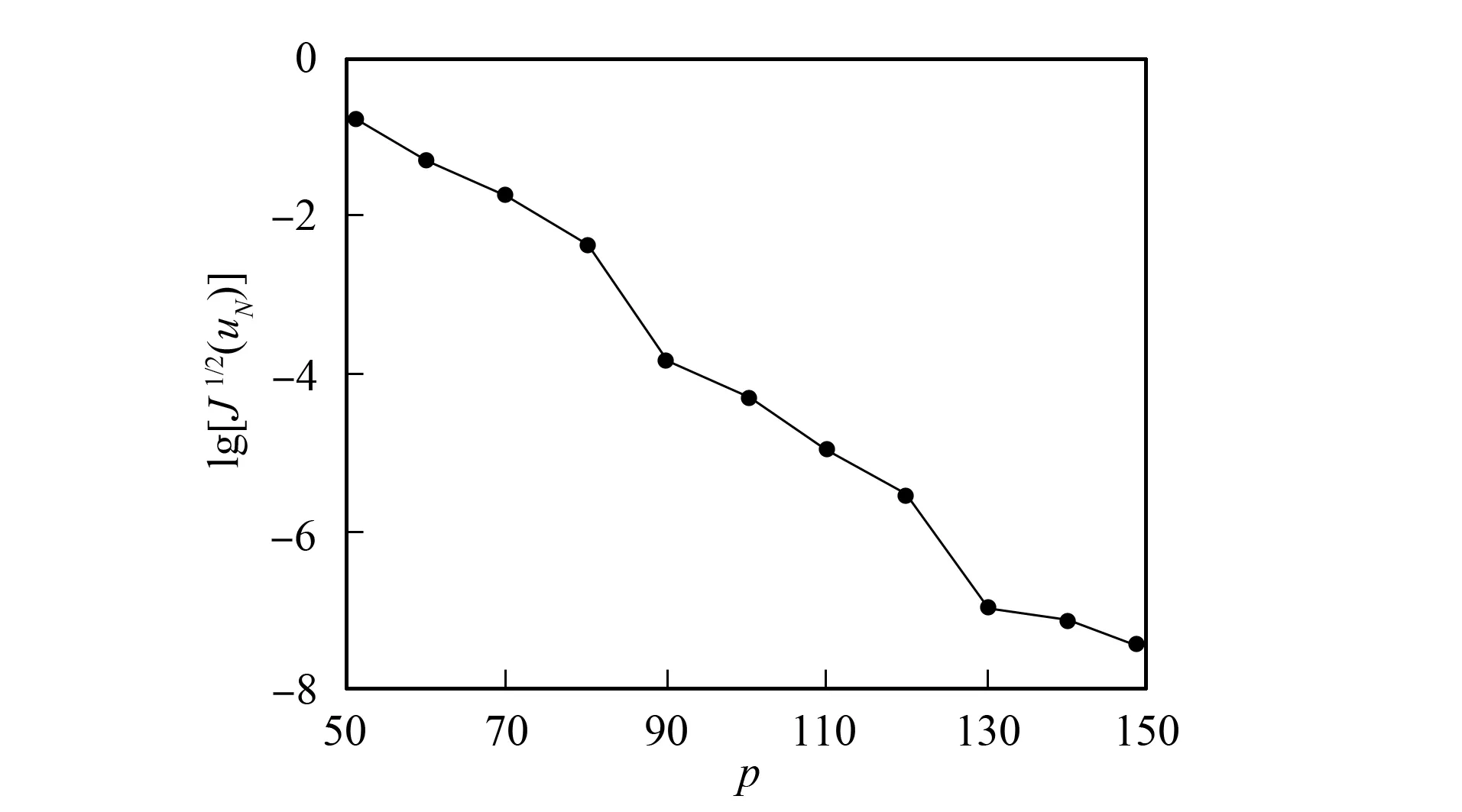
图8 例2的数值收敛结果Fig.8 Numerical convergence results of example 2

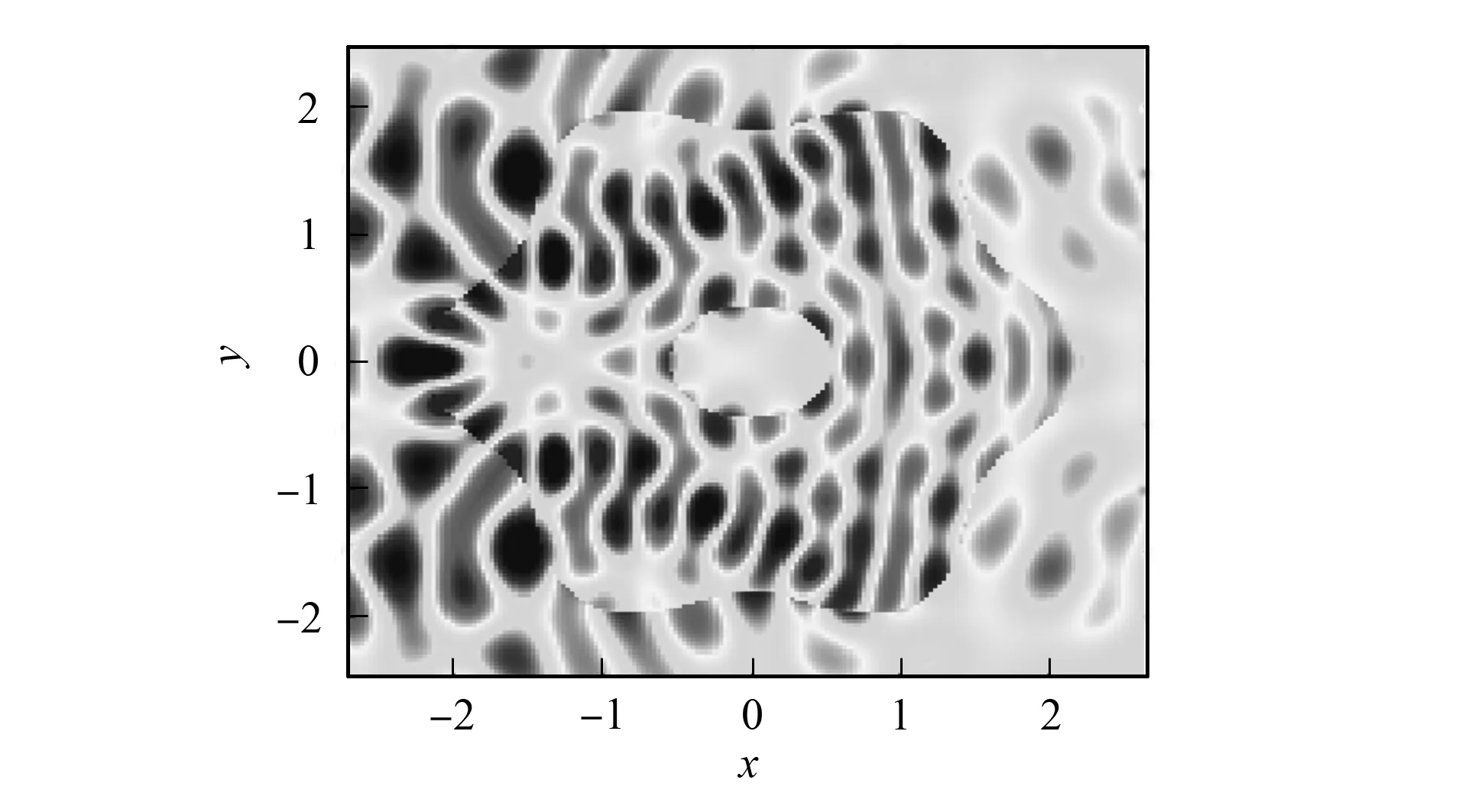
图10 例3的散射场us实部Fig.10 Real part of scattered field us of example 3

其次, 在D1内的闭曲线

γ1(δ)=((0.8+0.08cos(6δ))cosδ,(0.8+0.08cos(6δ))sinδ), 0≤δ≤2π

上选取如图9中第三圈圆点所示的离散点

图11 例3的全场u实部Fig.11 Real part of total field u of example 3

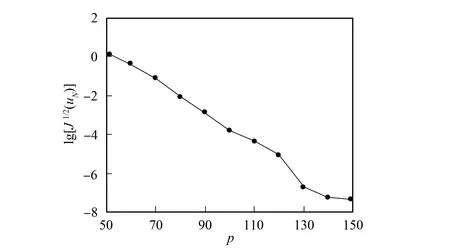
图12 例3的数值收敛结果Fig.12 Numerical convergence results of example 3