一类弱非线性奇摄动微分差分方程 的阶梯状空间对照结构

王 爱 峰

(淮阴师范学院 数学科学学院, 江苏 淮安 223300)

1 引言与预备知识

奇摄动微分差分问题在流体力学、 凝聚态物理、 光波散射、 神经网络等领域应用广泛[1-8]. 目前, 关于非线性奇摄动微分差分方程的内部层、 空间对照结构以及渐近解的一致有效性研究已引起人们广泛关注[9-11]. 本文考虑如下弱非线性微分差分方程：

的阶梯状空间对照结构, 在一定条件下证明了该问题在感兴趣的区间上存在转移点t*, 并指出由于时滞的影响, 在t=0处的边界层会对t=σ的内部层产生重要影响. 其中: 0<μ≪1是小参数;σ≥0是滞量;α(t)是定义在区间[-σ,0]上的光滑函数;T是正常数, 且σ≤T≤2σ.

首先, 做变换μy′=z, 则方程(1)可化为

μy′(t)=z(t),μz′(t)=F(z(t),y(t),y(t-σ),t).

下面给出一些假设条件.

(H1) 假设函数F(z,y,u,t)在其定义域内关于每个变量存在(n+2)阶的连续偏导数, 这里u=y(t-σ), 且0≤t≤T;

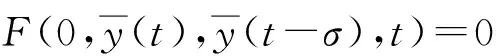
(H3) 假设当y(t)=φi(t)(i=1,3)或y(t)=ψ1(t)时,

Fy(0,y(t),y(t-σ),t)>0,Fy(0,φ2(t),φ2(t-σ),t)<0.

2 区间[0,T]上形式渐近解的构造

令x=(y,z)T, 设问题(1)-(2)在区间[0,t*],[t*,σ]和[σ,T]上的形式渐近解分别为

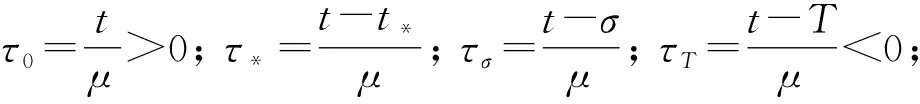
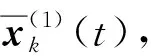
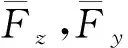
对L0x(τ0), 有

L0y(0)=α(0)-φ1(0),L0y(+∞)=0.

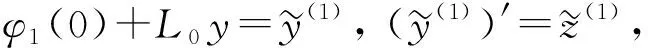
(6)

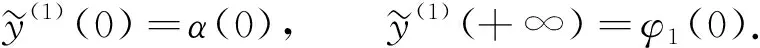
(7)

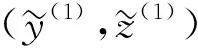
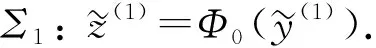
对Lkx(τ0), 有

(8)

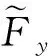
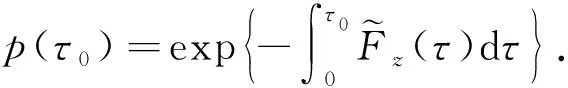
(9)

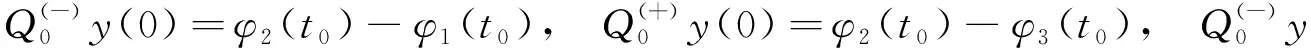
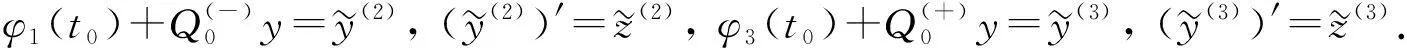
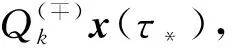
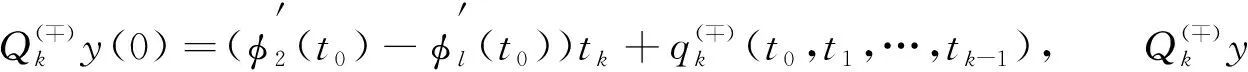
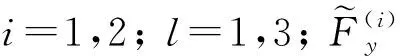
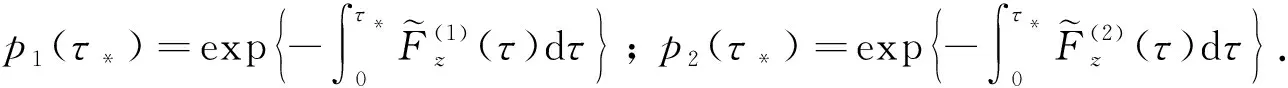
特别地, 在点t=σ处, 令

y(σ,μ)=p(μ)=p0+μp1+μ2p2+…+μkpk+…,

(10)

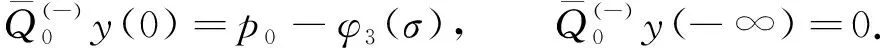
(11)

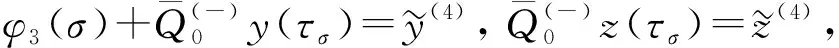
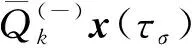
(12)

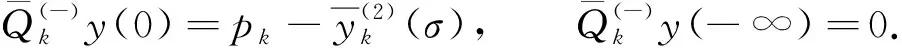
(13)

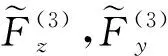
其中

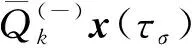
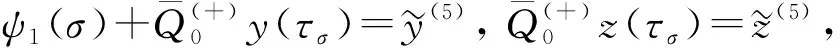
(14)

(15)

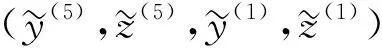
的特征根满足

所以平衡点M(ψ1(σ),0,φ1(0),0)是双曲鞍点. 因此通过平衡点M存在一个二维稳定子流形Ws(M)和一个二维不稳定子流形Wu(M). 令

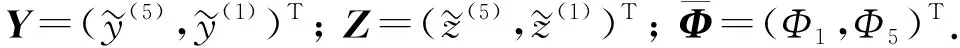
则

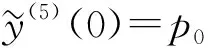
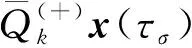
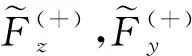
其中:

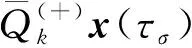
边界函数Rkx(τT)(k≥0)对内部层没有实质的影响, 其求解方法与Lkx(τ0)(k≥0)类似, 故略.

3 形式渐近解的光滑连接

为了得到在区间[0,T]上的光滑解,y(1)(t,μ)和y(2)(t,μ)必在点t=t*处光滑连接; 同时,y(2)(t,μ)和y(3)(t,μ)必在点t=σ处光滑连接, 即

将式(3)～(5)分别代入问题(16)-(17), 得

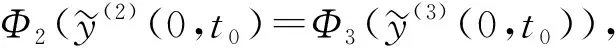
(24)

即为确定t0的方程.

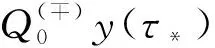
H′(t0)tk=γk,

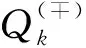
下面求pk. 令

(25)

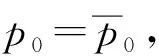
对pk, 由式(18),(23)得

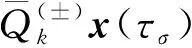
4 复合解的存在性

问题(1)-(2)的解可视为下列辅助问题解的光滑连接.

左问题(0≤t≤t*):

(26)

其中t*=t0+μt1+…+μn(tn+δ),δ是参数.

中间问题(t*≤t≤σ):

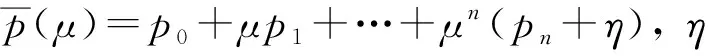
右问题(σ≤t≤T):

(28)

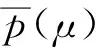
问题(26)～(28)是纯边值问题, 其解均存在, 且有下列形式:

由问题(26),(27)知,

y(1)(t*,μ)=y(2)(t*,μ),t*∈(0,1),

表明y(t,μ)在t=t*处连续. 因此,t*可由

z(1)(t*,μ)=z(2)(t*,μ)

确定. 下面引入函数

其中左右边界层级数系数在t=t*的邻域是指数小的.

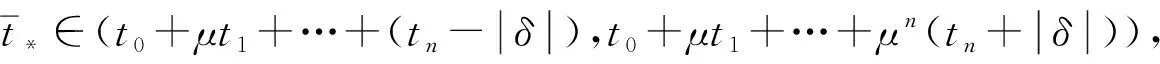
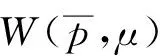
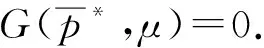
综上, 可得:

定理1在条件(H1)～(H5)下, 问题(1)-(2)的光滑解y(t,μ)在区间[0,T]上存在, 且如下形式的渐近展开式成立: