基于TDOA/FDOA多星联合定位误差与卫星构型分析

秦耀璐 杨淑萍 束锋,,3 孙琳琳 陆锦辉 许正文 桂林卿

(1.南京理工大学电子工程与光电技术学院,南京 210094; 2.中国电波传播研究所 电波环境特性及模化技术重点实验室,青岛 266107; 3.东南大学 移动通信国家重点实验室,南京 210096)

引 言

无源定位是指在不发射电磁波的条件下获得目标的位置. 利用小卫星平台,能进行大范围的搜索和电子侦察,基于卫星的高精度无源定位技术在导航、跟踪和电子对抗等军事和民用领域有着广泛的应用. 到达时间差(time difference of arrival, TDOA)定位技术利用由目标辐射源信号到达不同观测站的时间差确定的多个双曲面相交进行定位,到达频率差(frequency difference of arrival, FDOA)定位技术则利用目标辐射源与观测站相对运动产生的多普勒频移差进行定位. 相较于其他无源定位技术,无源TDOA定位精度较高. 若目标辐射源与观测站之间存在相对运动,利用FDOA信息可以进一步提高定位性能,TDOA/FDOA联合定位能很大程度地提高定位精度,因此联合定位技术有广阔的应用前景[1]. Ho在文献[2]中提出了利用TDOA/FDOA对运动目标进行定位的经典两阶加权的最小二乘(weighted least squares, WLS) 算法. 近年来,定位领域的国内外学者提出了许多利用TDOA和FDOA测量信息进行定位的算法[3-9]. 文献[3]提出了基于加权代价函数的TDOA/FDOA联合定位算法,避免了加权WLS算法存在的只能在一定的噪声环境中使得定位误差达到克拉美·罗界(Cramer-Rao lower bound, CRLB)的问题,使得定位对于噪声的稳定性大幅提高. 文献[4]提出了利用最大比合并技术基于最大似然原理的TDOA/FDOA定位算法,该算法的定位性能在有无地球约束的条件下均优于单独定位性能,并且逼近CRLB,但最大比合并的联合搜索定位算法实现复杂度较高. 文献[5]提出了基于网格搜索的加权最大似然代价函数定位算法,该算法与最大比合并的定位性能近似相等,但在复杂度上,节省了一半左右的计算量. 由于最大似然估计问题的非凸性质,如果没有良好的初步估计,难以获得全局最优解,因此,文献[6]将定位问题重新定义为加权最小二乘问题,将定位问题最终化成半正定松弛问题求解．TDOA/FDOA联合定位方法通常不具有直接的解决方案,并且需要数值方法来确定发射器的位置,文献[7]提出了解决非线性优化问题基于粒子群算法的TDOA/FDOA联合定位方法. 文献[8]研究了采用最陡下降法和最大似然估计法的分布式被动传感网络中移动目标源的TDOA/FDOA定位算法. 在最新的研究中,文献[9]将目标位置估计问题转化为二次约束二次优化问题,使用拉格朗日乘数法求得了近似解析解. TDOA/FDOA定位算法层出不穷,因而对评判定位算法性能的标准提出了迫切要求. 研究联合定位的CRLB[10],可以衡量各种定位算法的性能优劣,分析影响定位精度的各种因素.

Ho和Chan于1997年推导了多星TDOA和FDOA联合定位的误差CRLB[11],由此确定了无偏估计器中最优无偏估计器所能达到的最好定位性能. 孙仲康在文献[12]中推导了TDOA测量误差较小情况下的多星TDOA定位方差. Pattison和Chou在文献[13]中分析了双星联合定位的几何精度因子(geometric dilution of precision, GDOP)和方差,发现TDOA定位曲面、FDOA定位曲面与地球表面夹角为90°时定位精度最好. 文献[14]和文献[15]对双星联合定位算法和误差分析进行了更深入的研究. 由于Ho推导的联合定位方差公式CRLB并不适合于TDOA/FDOA三星单独定位,故文献[16-17]讨论了三星定位误差分析. 文献[18]分析了多星TDOA/FDOA联合定位中时差误差和频差误差对定位精度的影响. Ho等[2]于2007年在考虑接收机位置和速度存在测量误差情况下,推导了运动目标多星联合定位的方差下界,即CRLB,但是未能给出显式表达式.

本文将应用Taylor级数、矩阵理论和统计理论等多种手段进行简化处理获得静态目标的方差CRLB显式表达式,有效地简化定位精度分析. 同时考虑到三星单独定位不能直接应用该式,我们将双星的联合定位误差推导思路应用于三星单独定位情况,并获得其定位误差公式. 进一步,本文分析和讨论了多星卫星构型对定位性能的影响. 仿真结果表明,FDOA较容易产生定位盲区,且该盲区无法通过卫星构型设计来避免,而TDOA的定位盲区可以通过设计良好的卫星构型完全消除. 此外,TDOA/FDOA联合定位时,能有效避免TDOA或FDOA带来的定位盲区,且能显著提高定位精度.

1 系统模型

三维空间的多星无源定位系统由M个卫星组成,位置向量为ri=(xi,yi,zi)T(i=1,2,…,M),未知目标源位置坐标向量为r=(x,y,z)T. 从未知目标源到卫星i的单位位置向量可表示为

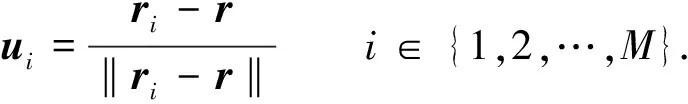
(1)

目标源到任何两对卫星j和i的TDOA 和FDOA可表示为

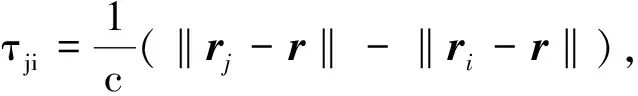
(2)

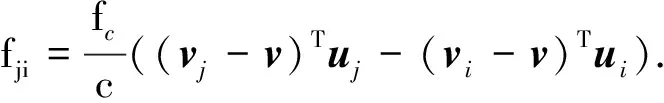
(3)

式中:c表示光速;fc为目标源载波频率;vi和v分别为卫星i和目标源的运行速度. 考虑卫星位置误差与速度误差,对式(2)和式(3)进行Taylor展开,得到如下表达式:

Δτji=τji(r+Δr,ri+Δri,rj+Δrj)-τji(r,ri,rj)

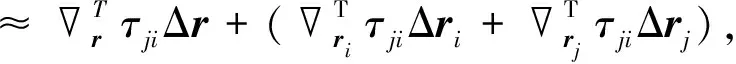
(4)

Δfji=fji(r+Δr,ri+Δri,rj+Δrj,vi+Δvi,

vj+Δvj)-fji(r,ri,rj,vi,vj)

(5)

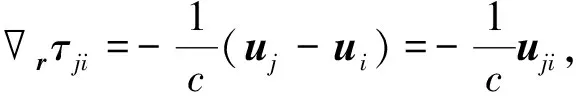
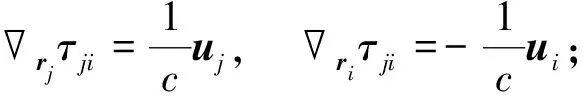
(6)

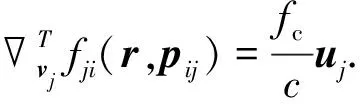
(7)

式中,βi和pij表示为

pij=ri-rj．

(8)

选择卫星1为主星,收集所有的时差和频差构成TDOA和FDOA向量,共有N=M-1个独立时差和频差对,即

Δτ=(Δτ21,Δτ31,…,ΔτM1)T,

Δf=(Δf21,Δf31,…,ΔfM1)T.

(9)

将时差向量和频差向量合成大的向量,定义如下向量矩阵表达式

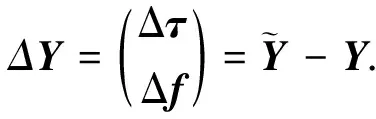
(10)

考虑TDOA和FDOA测量误差、卫星自定位误差,以及卫星速度测量误差的影响,利用式(4)～(7),定位误差方程可近似表示为向量矩阵形式

Y(r,rs+Δrs,vs+Δvs)-Y(r,rs,vs).

(11)

式中:r表示目标位置;rs+Δrs表示测量获得的卫星位置,rs为卫星实际位置,Δrs为卫星位置测量误差;vs+Δvs表示测量获得卫星的速度向量,vs为卫星实际速度向量,Δvs为卫星速度向量测量误差;而

Y(r,rs+Δrs,vs+Δvs)-Y(r,rs,vs)=Δrs+Δvs．

(12)

令

(13)

于是式(11)更改为

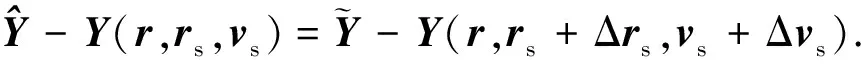
(14)

由式(14)有

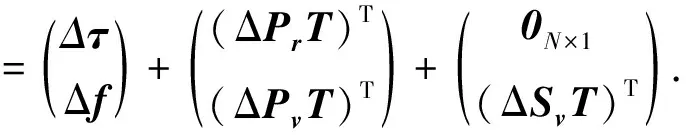
(15)

式中:左边表示定位误差;右边第一项表示TDOA/FDOA测量误差,第二项表示卫星自定位误差,最后一项表示卫星速度测量误差,均服从高斯分布．式(15)中各矩阵向量可表示如下:

T=(-e,IM-1)T.

(16)

式中:

Δri=Δr1+Δri1,i∈{2,3,…,M};

e=(1,1,…,1)T;

(17)

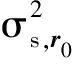
2 多星定位误差分析

2.1 多星TDOA/FDOA联合定位误差

基于式(14)和(15)得到接收的时差频差联合向量概率密度如下[10]:

(18)

我们得到Fisher信息矩阵[10]

J=E{[lnp(Y;r)][lnp(Y;r)]T}

(19)

式中,

Gr=(Gτ,rGf,r),

(20)

Gτ,r与Gf,r均为3×N(N≥3)的矩阵．定义

u=(u1,u2,…,uM),β=(β1,β2,…,βM),

T=(-e,IM-1)T,

(21)

利用矩阵T,结合式(8)和式(21),得到:

(22)

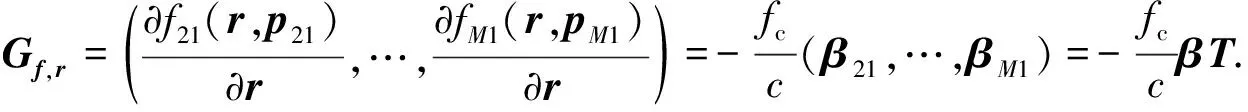
(23)

以及

Σ=E{ΔYΔYH}

(24)

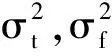
GDOP2(x,y,z) =tr{J-1}

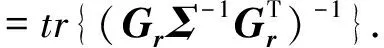
(25)

当考虑地球约束[11]时,

(26)

式中,re为地球半径．则受地球约束的多星TDOA/FDOA联合定位的GDOP为

GDOP2(x,y,z)=tr{J-1-J-1F(FTJ-1F)-1FTJ-1}.

(27)

式中,F=(2x,2y,2z)T. 上面推导的多星GDOP,也可称为CRLB联合公式,适用于四星及以上单独定位系统和三星及以上联合定位系统. 因此,我们将在下节推导考虑地球约束后的三星TDOA单独定位误差公式.

2.2 三星单独定位误差

上节推导的多星联合公式不适用于三星单独时差或频差定位,主要原因是仅有两个测量参数,导致Fisher信息矩阵为奇异矩阵,无法求逆. 本节将以TDOA为例,专门推导三星单独TDOA定位的GDOP.

对于三星单独定位,两测量参数加上地球约束三个方程恰好可联立求解目标的位置向量,其思路类似于双星TDOA/FDOA. 类似于文献[19],考虑卫星位置测量误差后,如式(2) 所示的TDOA定位方程以及式(26)地球约束依据Taylor级数可展开为:

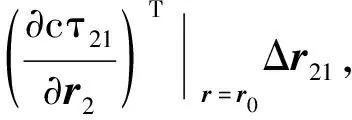
(28)

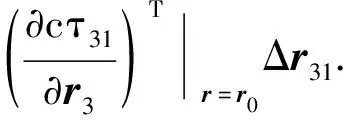
(29)

0=(2x,2y,2z)T|r=r0Δr

(30)

式中:Δr为定位目标的误差项;Δr1为卫星1也就是主星的绝对测量误差,Δri1为卫星i相对于主星的相对测量位置误差,即Δri=Δr1+Δri1,i∈{2,3}. 为表达方便,下面推导中忽略r=r0. 将式(28)～(30)组合成矩阵向量形式,有

Δd=HΔr+H1Δr1+ΔH2．

(31)

式中:

H=(-u21,-u31,2r)T;

H1=(u2+u1,u3+u1,03)T;

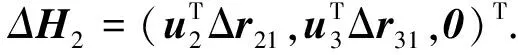
(32)

其中ui和uji见式(1)和式(6),03表示全零的三维列向量. 由式(31)得到

Δr=H-1(Δd-H1Δr1-ΔH2)．

(33)

根据GDOP的定义,我们有

GDOP2(x,y,z) =tr{E(ΔrΔrT)}

(34)

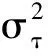
3 卫星构型设计讨论

地球半径re=6 378.137 km,以五星为例分析多星构型,图1是五星的定位系统图. 地心为O,其中主星为A,副星为B、C、D和E. 星下点定义为主星和地心的连线与地球表面的交点,星下点为S. 主星高程为h,假定目标位于P处,θ表示主星-副星连线与主星-星下点连线夹角.AB=AC=AD=AE为主副星之间的距离. 给定主星的位置,四颗副 星的经纬度坐标及高程随θ变化而变化. 由于卫星间距一般在10 km到200 km之间变化,此值同卫星高程与地球半径相比可忽略. 考虑到五星编队飞行,于是五颗卫星速度向量可近似为相等.

图1 五星定位系统框图Fig.1 Block diagram of five-satellite localization system

定理1 目标位于地球表面且距离星下点距离为Rkm范围无定位盲区充分条件:主星-副星连线与主星-星下点连线夹角θ满足φ<θ<180°-φ.

证明:

当目标P位于距离星下点Rkm圆周上时,对应的∠AOP为

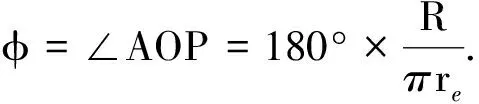
(35)

利用此角度可获得线段AP长度等于

(36)

于是,可得∠PAO=φ如下:

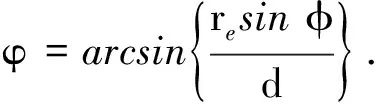
(37)

若φ>θ,显而易见,在AC延长线与地球表面交点至P点一段存在定位盲区. 为了保证在星下点Rkm范围内不出现定位盲区,令φ≤θ,考虑目标P距离星下点Rkm,且位于主星-副星连线AC的延长线与地球表面交点附近,此时φ=θ,即主星A、副星C、目标P在同一条直线上. 令主星A为卫星1,副星C为卫星3,由ui的定义式,且由于卫星间距变化与同卫星高程和地球半径相比可忽略,得到u3=u1,即

u31=u3-u1=0．

(38)

仅考虑单独TDOA定位时差测量误差,式(25)简化为

GDOP2(x,y,z) =tr{J-1}

(39)

(40)

根据Cauchy-Schwarz不等式可得

=9．

(41)

由式(41),有

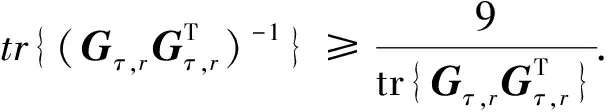
(42)

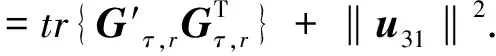
(43)

目标P位于主星-副星连线的延长线与地球表面的交点附近,利用式(38),得到‖u31‖2=0. 由式(43)可知,相较于其他区域,目标位于主星-副星连线的延长线与地球表面的交点附近时,定位性能下降,形成定位盲区.

同理,当θ>180°-φ,即θ+φ>180°,AE的反向延长线与地球表面的交点至目标P一段存在定位盲区.

令θ=180°-φ,即目标P位于AE的反向延长线与地球表面交点附近,可以得到,此时定位性能下降,该处形成定位盲区,证明同上.

综上,为了保证在星下点Rkm范围内不出现定位盲区,四颗副星与主星连线同主星到星下点连线的夹角θ必须满足下面不等式:

φ<θ<180°-φ．

(44)

证毕.

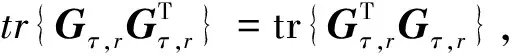
(45)

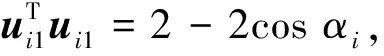
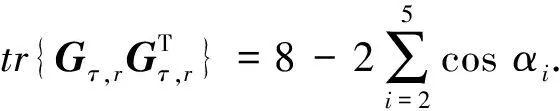
(46)

通过分析式(42)和(46)可知,增大αi可提高定位性能,当保持主副星之间的间距不变时,αi随相邻主星-副星连线间夹角βi的增大而增大. 如图1所示具有良好对称结构的卫星构形βi均为β,即∠BAC=∠BAE=∠CAD=∠DAC=β,利用余弦定理可得β与θ关系为

cosβ=cosθ2．

(47)

当θ=90°时,β取得最大值90°.因而主星-副星连线与主星-星下点连线夹角θ趋于90°时,则主星-目标连线与副星-目标连线的夹角αi越大,定位性能越好.

4 仿真分析

设置系统仿真参数如下:TDOA测量误差为50 ns,FDOA测量误差5 Hz. 采用五星定位系统,主星位于上方顶点,高程为h=1 000 km,东经130°,北纬0°,其他四颗副星位于主星下方构成正方形,主星到副星间距保持150 km不变,主星到其他四副星连线同主星到星下点连线夹角均为θ.

4.1 卫星构型对GDOP的影响

图2、图3和图4分别绘出了θ=40°,θ=70°时,TDOA单独定位的GDOP曲线、FDOA单独定位的GDOP曲线以及TDOA/FDOA联合定位的GDOP曲线.

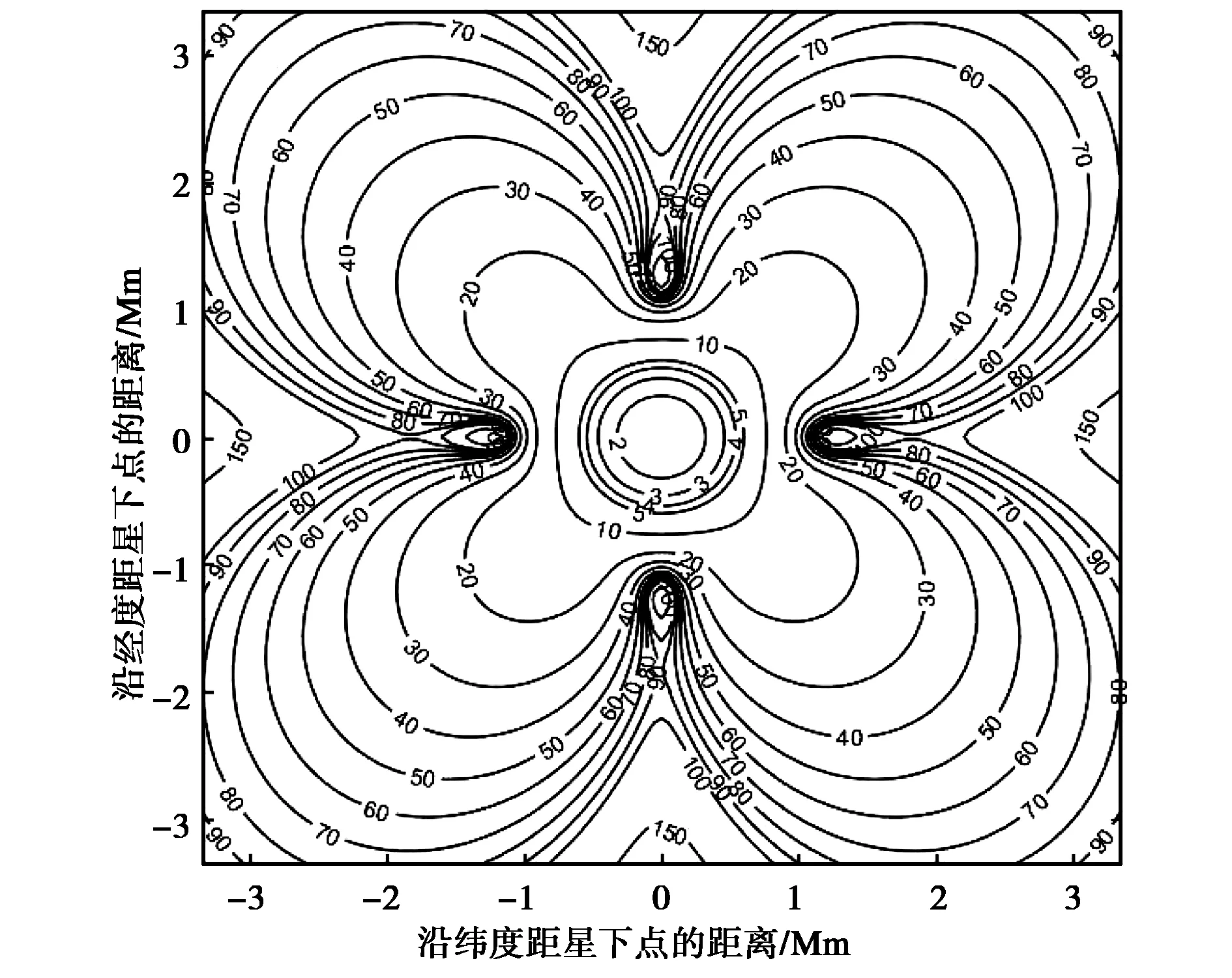
(a) θ=40°

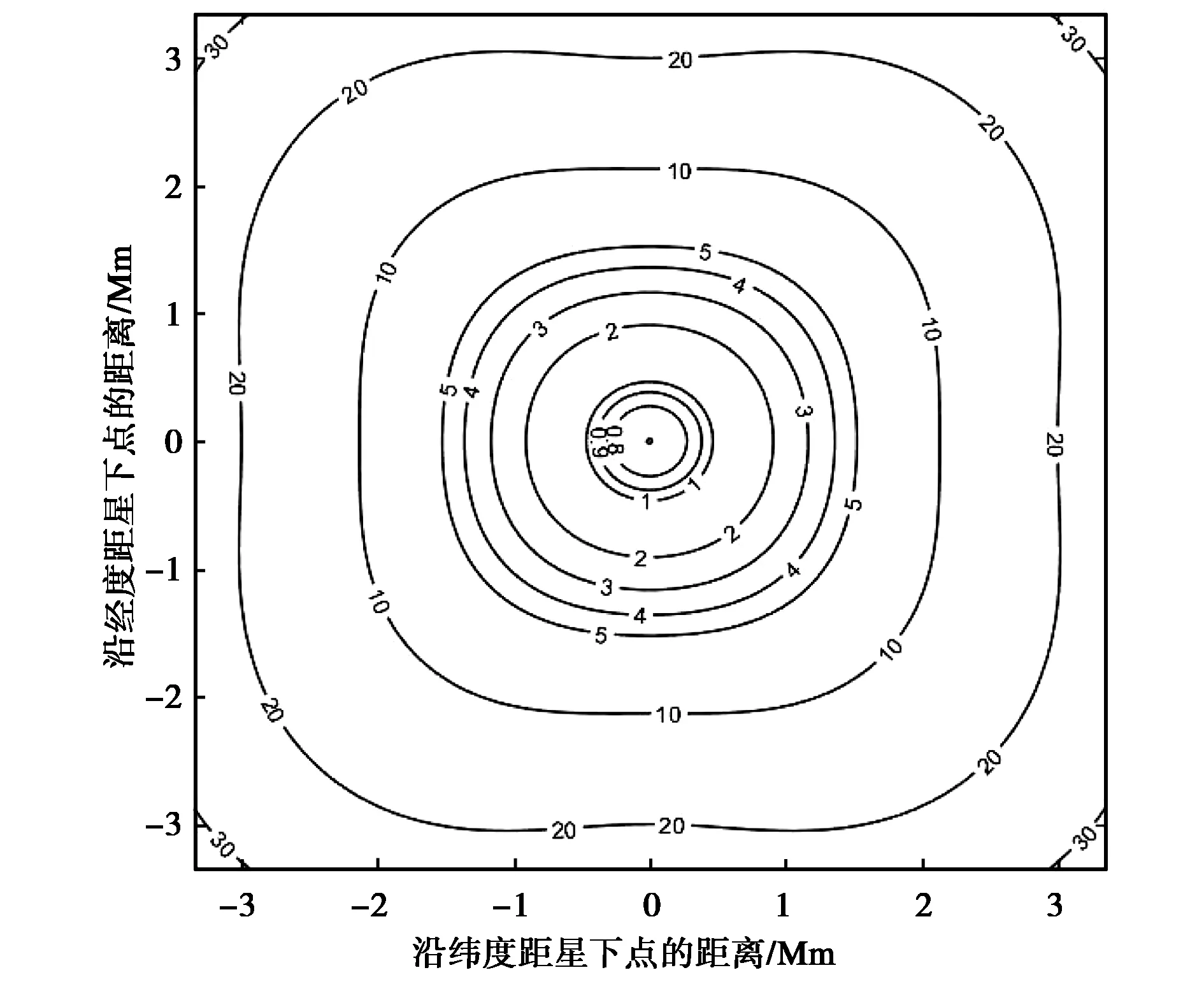
(b) θ=70°图2 TDOA单独定位的GDOP曲线Fig.2 GDOP of TDOA localization

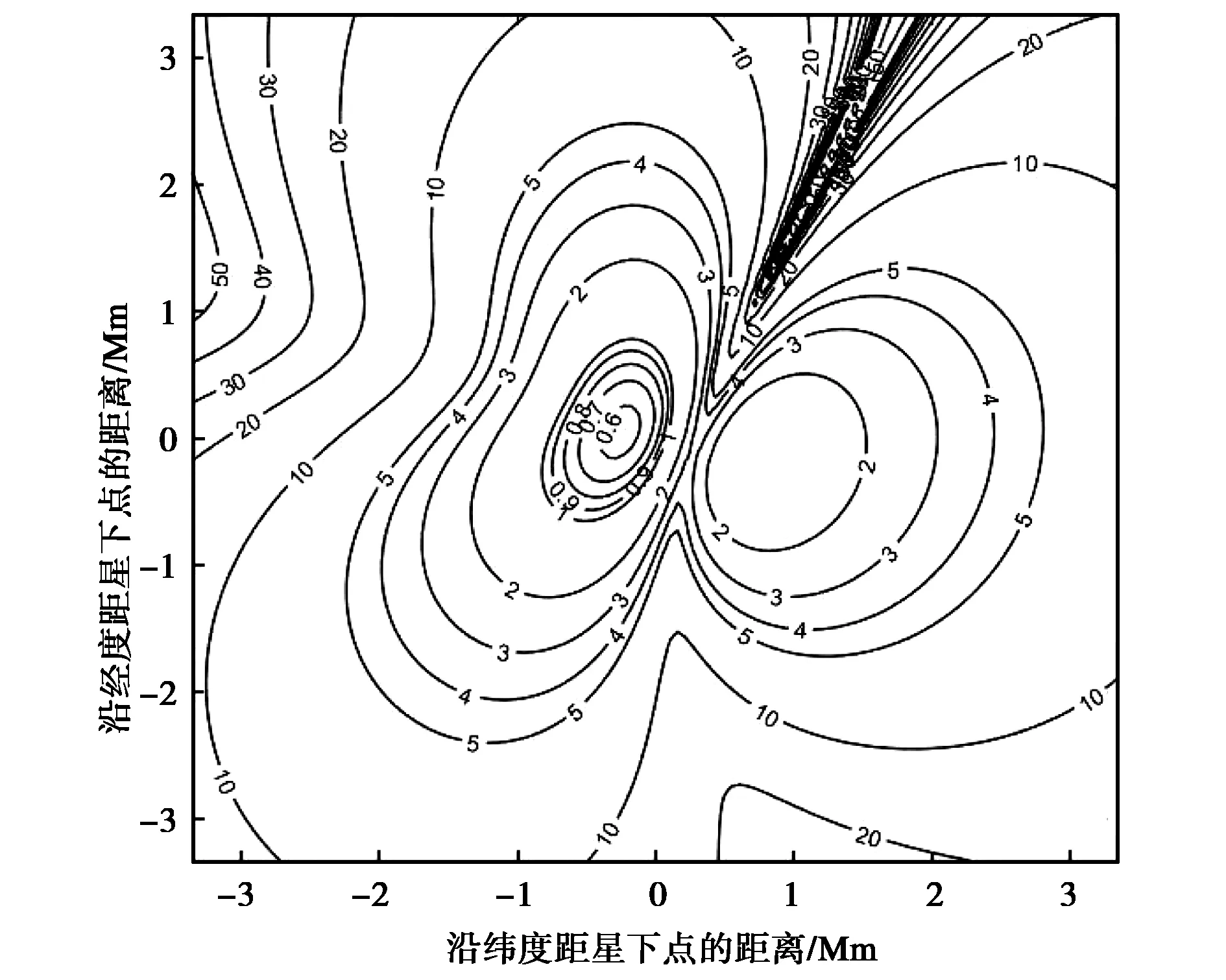
(a) θ=40°

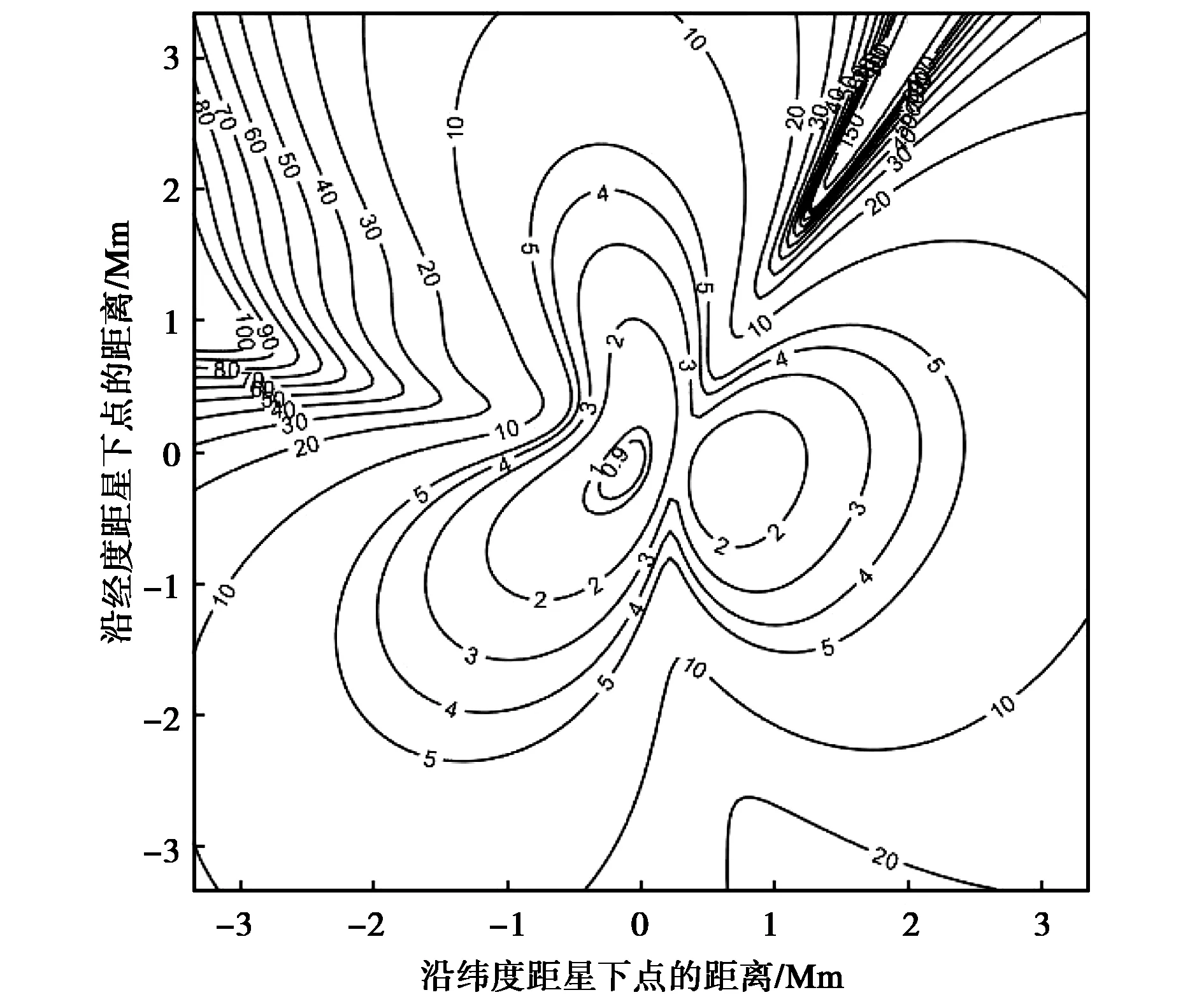
(b) θ=70°图3 FDOA单独定位的GDOP曲线Fig.3 GDOP of FDOA localization

(a) θ=40°

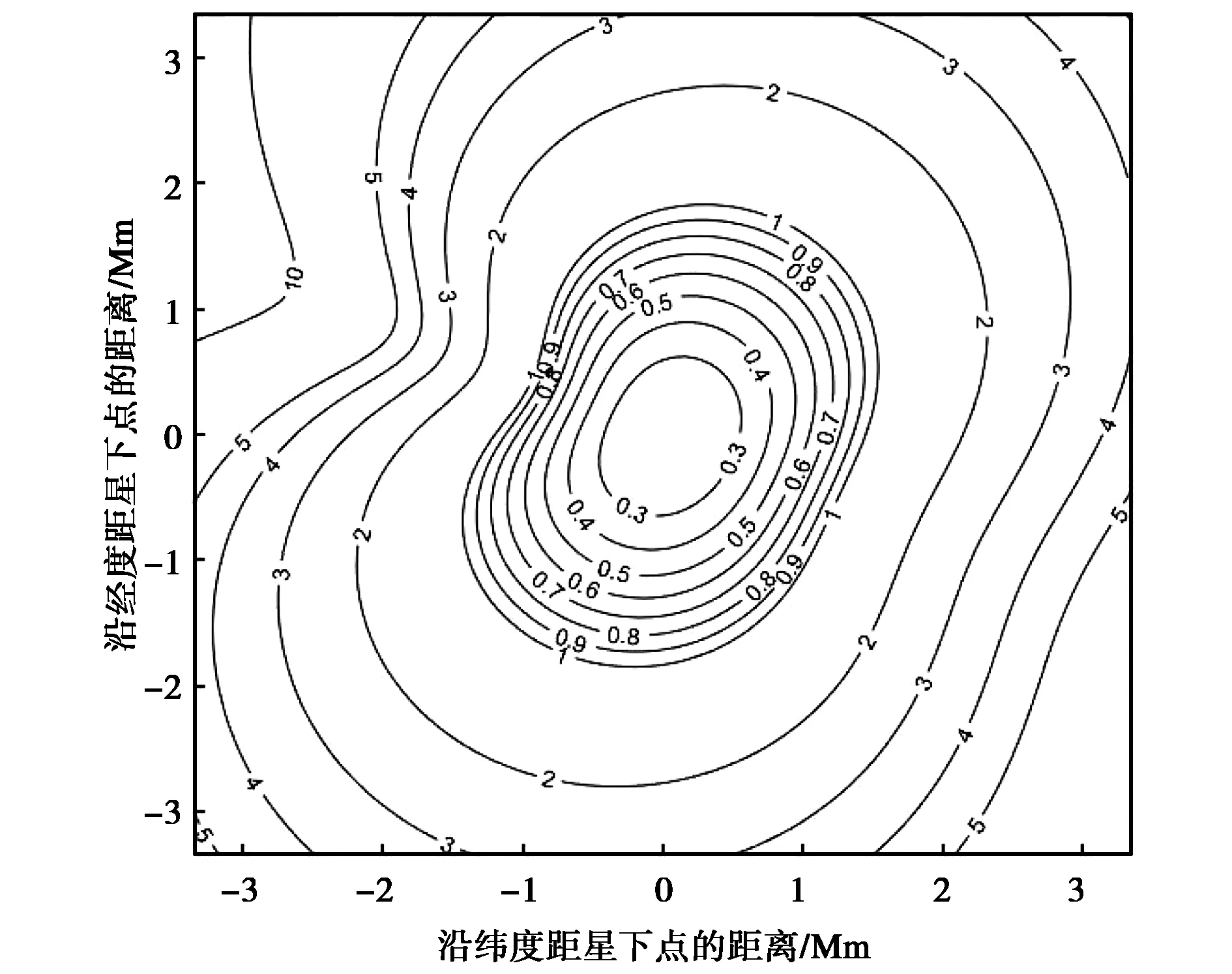
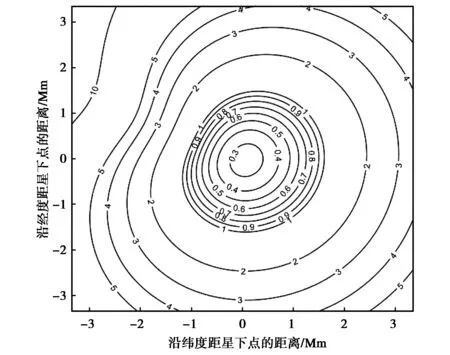
(b) θ=70°图4 TDOA/FDOA联合定位的GDOP曲线Fig.4 GDOP of joint TDOA and FDOA localization

由图2(a)可知,当θ=40°时,TDOA单独定位存在四个定位盲区,它们由主星-副星连线与地球交点附近区域形成盲区. 在设计卫星构型时尽量保证所有主星-副星连线与地球不相交,则可避免这些定位盲区. 图2(b)示出了θ=70°时定位盲区已经消除. 比较图2(a)和图2(b)发现TDOA在星下点的单独定位精度由2 km提升到0.8 km,远离星下点精度也有显著提升,因此增加θ角可提高TDOA定位精度.

仔细观察图3会发现:有一条通过星下点的定位盲区,此盲区内FDOA的定位误差较大．该盲区实际上是垂直于卫星速度方向通过主星的平面同地球相交圆周形成,由于卫星绕地球飞行,此平面与地球表面肯定相交,因此定位盲区是没有地球约束FDOA定位系统本身所固有的. 产生物理机制如下:此圆周上任意一点到卫星连线近似垂直于卫星速度方向,因此速度在此连线上没有分量,产生的Doppler频率为零,不起任何作用,也就是不提供任何定位信息. 因此角度变化对FDOA定位盲区消除没有影响.

结合图4(a)和图4(b)可知θ角度变化对联合定位精度基本没有影响．比较图2、图3和图4可知,TDOA/FDOA联合定位时,不存在定位盲区,且相较于TDOA单独定位和FDOA单独定位,定位精度明显提高.

4.2 卫星位置误差、卫星速度误差对GDOP的影响

系统仿真参数设置如下:主星到其他四副星连线同主星到星下点连线夹角均为θ=70°.

图5绘出了卫星位置绝对误差和相对误差为1 000 m、100 m,及100 m、10 m两种情况下TDOA/FDOA联合定位精度随离星下点距离的变化曲线. 由图5可知:当卫星位置绝对误差为100 m,相对误差为10 m时,卫星位置误差对定位精度近乎没有影响;在卫星位置绝对误差为1 000 m,相对位置误差为100 m时,卫星位置误差较大,卫星位置对定位精度的影响已经凸显,相较于卫星位置绝对误差为100 m相对误差为10 m,定位精度下降约1.2 km. 图6绘出了卫星速度误差分别为2 m/s,10 m/s时,TDOA/FDOA联合定位精度随离星下点距离的变化曲线. 由图6可知,卫星速度误差对定位精度影响较大. 相较于无卫星速度误差的TDOA/FDOA联合定位,对距星下点2 000 km左右的区域,卫星误差为2 m/s时,定位精度下降约3 km;卫星误差为10 m/s时,定位精度下降约6 km. 比较图5与图6可知,卫星位置误差提升一个数量级,定位精度约下降1.2 km,而卫星速度误差由2 m/s增大至10 m/s,定位精度平均下降约2.7 km. 速度测量精度对定位精度的影响较大,而测距精度对目标定位精度的影响较小. 图7绘出了同时考虑卫星位置误差和速度误差,TDOA/FDOA联合定位精度随离星下点距离的变化曲线. 比较图5和图6可知,当卫星位置误差较小时,速度误差为影响定位精度的主要因素. 同时图7示出综合考虑位置误差与速度误差,当位置误差达到一定量级时,卫星位置误差将会使定位精度产生大幅度下降.

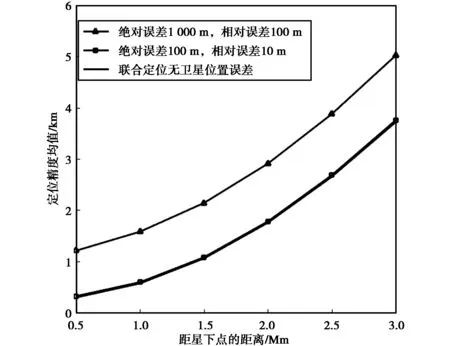
图5 卫星位置测量误差对定位精度的影响Fig.5 The effect of satellite position measurement errors on location accuracy

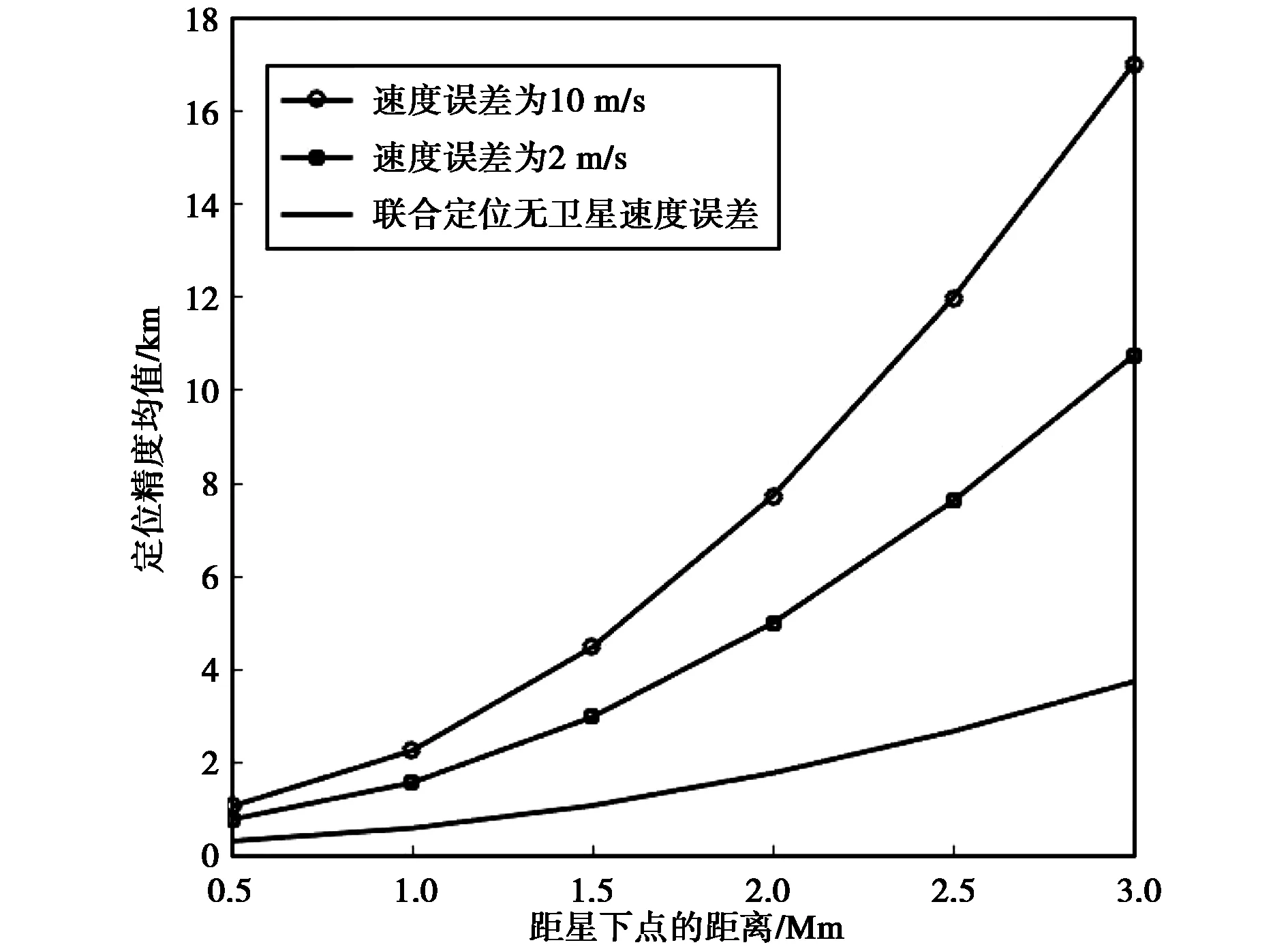
图6 卫星速度测量误差对定位精度的影响Fig.6 The effect of satellite velocity measurement errors on location accuracy

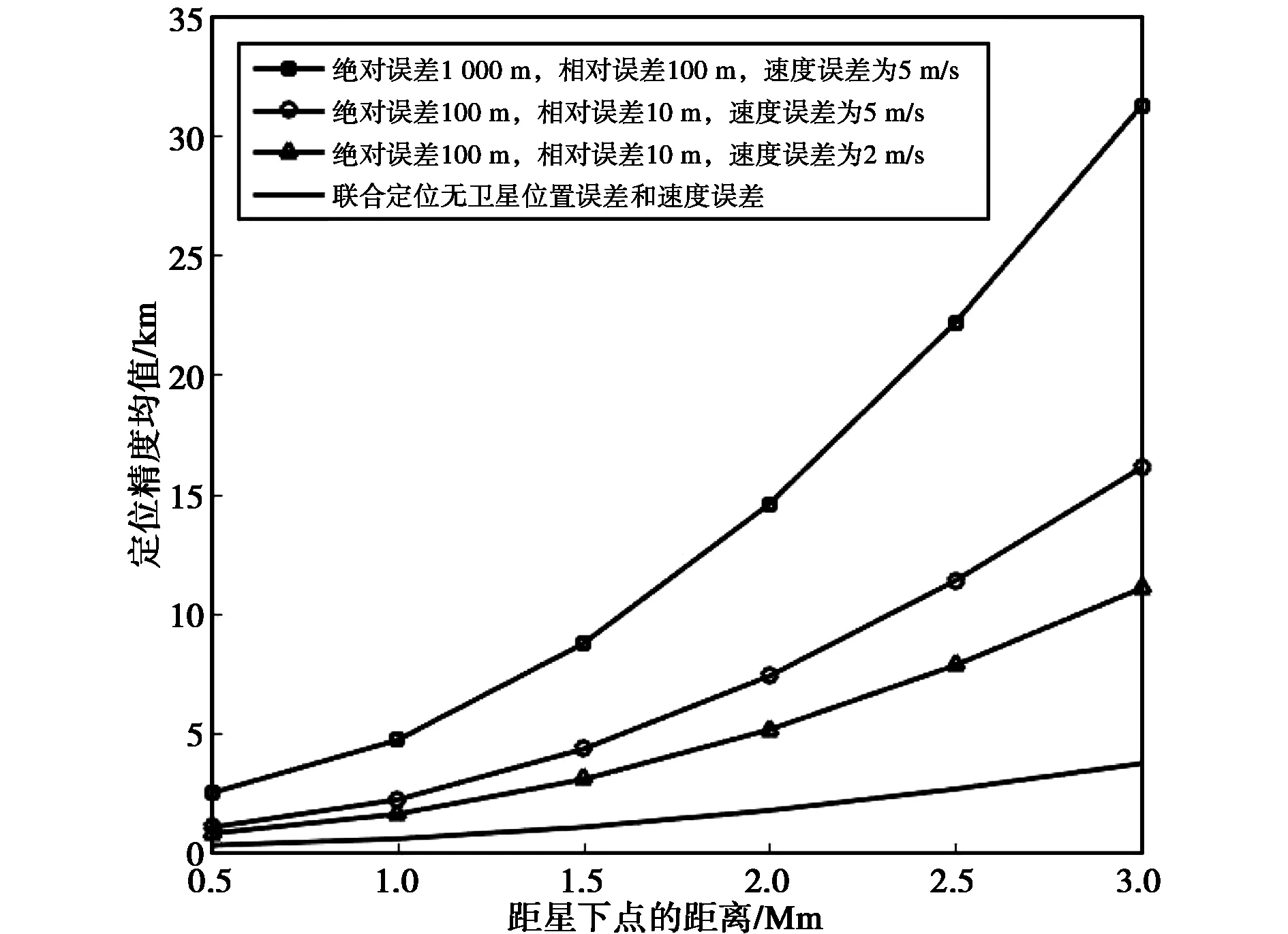
图7 卫星位置和速度测量误差对定位精度的影响Fig.7 The effect of satellite position measurement and velocity measurement errors on location accuracy

5 结 论

本文推导了多星TDOA/FDOA联合定位的误差公式,该公式充分考虑了TDOA测量误差、FDOA测量误差、卫星自定位误差和速度测量误差. 并且对卫星自定位误差与速度误差进行仿真分析,发现卫星速度误差是影响定位精度的关键因素. 最后对卫星构型进行了简单的讨论. 由此可见,良好的卫星构形、高精度的卫星速度测量与TDOA/FDOA联合定位相结合可以保证相当高的定位精度．