考虑局部非线性结构振动的模型预测控制

李 飞， 张 盛， 彭海军， 陈飙松

（大连理工大学 工业装备结构分析国家重点实验室 工程力学系，大连116024）

1 引 言

近年来，随着结构减震技术的发展，在建筑结构中经常会预设若干的非线性构件或非线性阻尼器等耗能装置，以便提高结构的抗震能力。这类耗能单元的引入可能对整个结构系统产生非线性力学效应，使得在设计计算和执行控制时，将面临大量的迭代求解，特别是对于大规模结构，该过程将十分耗时且难以收敛。因此，针对这类局部非线性结构振动控制问题，发展行之有效的非线性结构动力学分析方法和控制策略十分必要。目前，针对结构的非线性控制问题，已有的非线性控制算法主要包括多项式控制［1］、脉冲控制［2］、非线性最优控制［3］、加速度控制［4］、动态线性化方法［5］、滑动模态控制［6］、模型预测控制［7］、模糊控制［8］以及鲁棒控制［9］等。本文采用模型预测控制方法开展了局部非线性结构振动控制的相关研究。

模型预测控制 MPC（Model Predictive Control）是基于预测模型的一种现代先进控制技术。该技术吸取了最优控制思想，在每一个采样时刻，以当前状态作为预测过程的初始状态，通过在线求解一个有限时域的开环最优控制问题，得到该时刻的最优控制力序列，并将该序列中第一个控制力施加于被控系统。进而随采样时间步进，完成整个控制过程。事实上，自从Richalet等［10］首先发表了关于该算法的产生背景及应用效果以来，MPC已经应用于各个工程领域，如土木工程［11］、机械工程［12］和航空航天工程［13］等。然而，以上工程应用大多属于线性系统，在处理非线性系统时，MPC仍存在较大待改进的空间。如模型预测控制的在线预测计算时间应小于控制采样周期［14］，但对于具有局部非线性复杂结构振动控制问题，由于其动力学微分方程的非线性而需要大量的迭代求解，特别是面对大规模结构，当外激励的采样时间较小时，预测时间将很难满足要求。

因此，为设计行之有效的控制器，本文首先推导了局部非线性结构动力响应时域显式递推表达式。然后，利用该表达式建立了局部非线性结构振动预测模型，并采用模型线性化方法对非线性环节进行处理，提出考虑局部非线性结构振动的模型预测控制算法。另外，在获取各仿真时刻的预测初始状态时，为避免直接对非线性方程的所有维度完全迭代求解，给出了考虑局部非线性结构动力学的时域显式降维迭代方法［15］，以缩小迭代规模，提高在线的非线性动力学求解效率，完成整个控制过程。最后，分别以局部非线性弹簧振子动力系统和含粘滞阻尼器的毗邻框架结构振动控制系统为例，验证了所提算法计算准确且控制效果较好。

2 局部非线性结构动力响应时域显式递推表达式

考虑n个自由度的局部非线性结构系统，在外部激励和主动控制力作用下，其动力学微分方程为

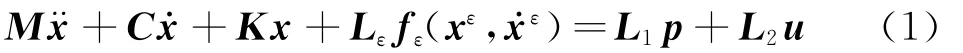
式中 M∈Rn×n，C∈Rn×n和K∈Rn×n依次为结构质量矩阵、阻尼矩阵和刚度矩阵；x∈Rn×1，x·∈Rn×1和x¨∈Rn×1依次为结构运动的位移向量、速度向量和加速度向量；xεx和x·εx·分别为与非线性相关的局部位移和速度；fε（xε，x·ε）∈Rq×1为q维的局部非线性外力向量；p∈Rr×1为r维的外激励向量；u∈Rm×1为m 维的作动器控制力向量；Lε∈Rn×q，L1∈Rn×r和L2∈Rn×m为相应作用载荷的定位矩阵。

将式（1）的非线性项移至等式右端，可得拟线性微分方程（2），

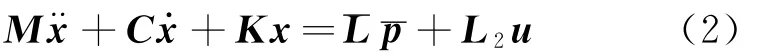
式中

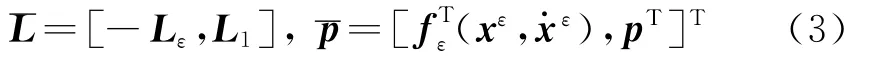
采用Newmark－β法对式（2）进行数值离散。假设在ti（i＝1，2，…，nt－1，nt；nt为数值仿真步数）时刻的速度和位移［16］为

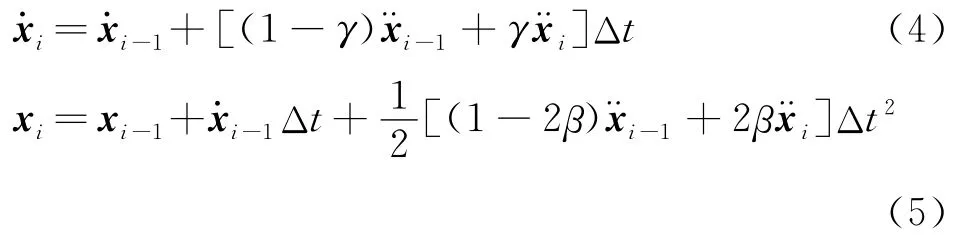
式中 Δt为积分步长；γ和β为Newmark－β的算法参数 （γ≥0．5，β≥0．25（0．5＋γ）2），可根据积分精度和稳定性要求确定，本文取γ＝0．5，β＝0．25。

系统在ti和ti－1时刻的动力学平衡方程依次为

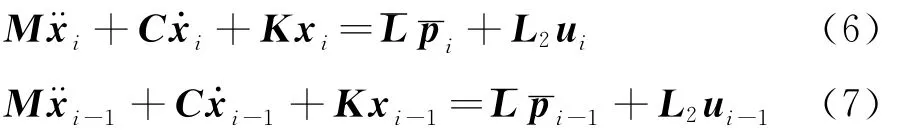
由式（6）得

式中

式中 积分参数aj（j＝0，1，2，3，4，5）依次为

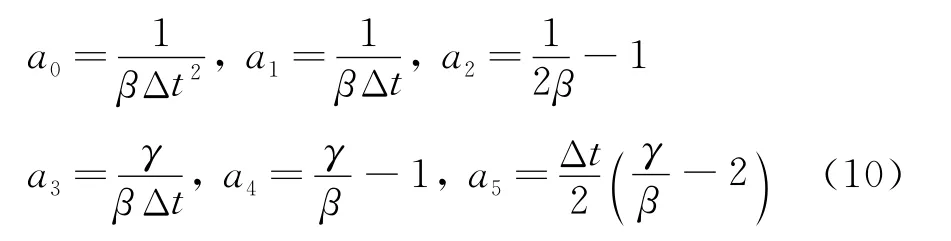
由方程（7）可得

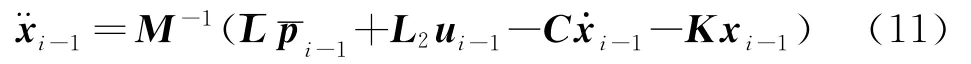
将式（11）代入式（9），则由式（8）整理可得

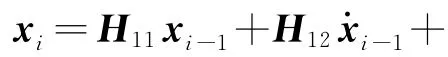
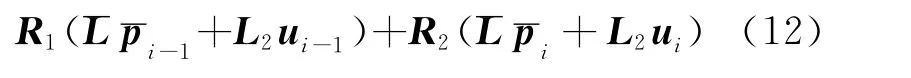
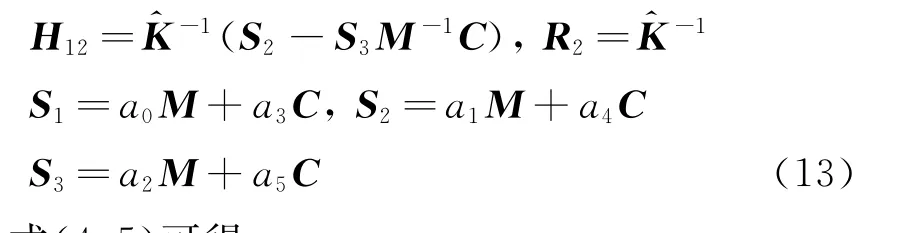
联立式（4，5）可得

将式（11）代入式（14）整理得

式中 H21＝a3（H11－I）＋a5M－1K

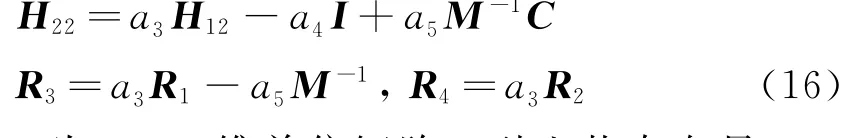
式中I为n×n维单位矩阵。引入状态向量v＝［xT，x·T］T，则由式（12，15）可得结构响应的时域递推表达式为

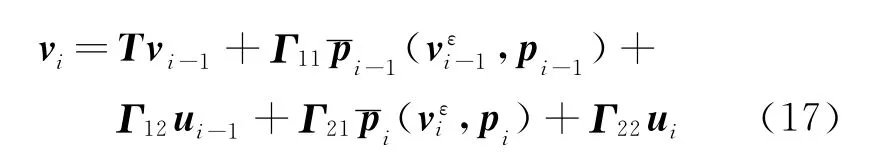
式中

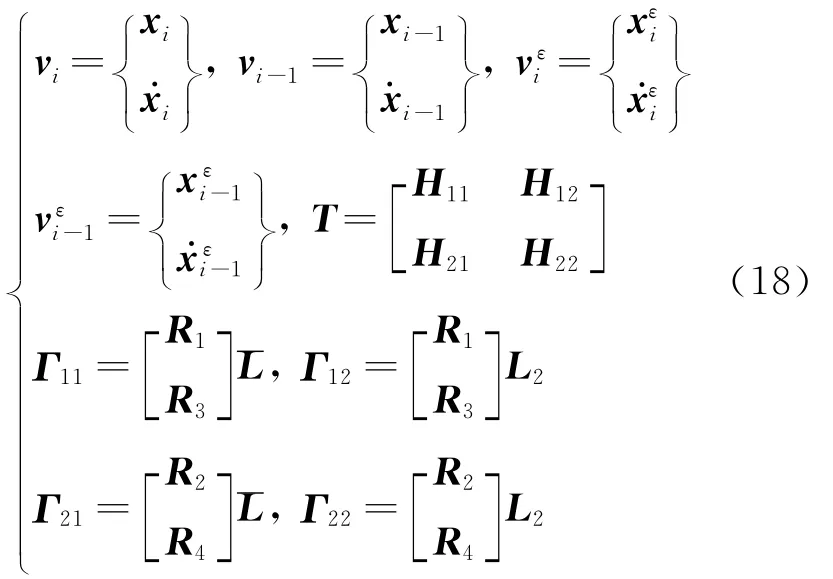
式（17）即为考虑局部非线性结构振动时域显式递推表达式。

3 局部非线性结构振动的模型预测控制

首先，根据模型预测控制理论［14］，在控制器设计时，忽略动力学方程（1）的外激励L1p作用。假设预测的时间为T，预测的步长为δt，预测的时间步数为Nt＝T／δt，则可将式（1）写为

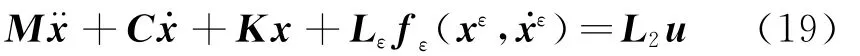
然后，类比于第2节局部非线性结构振动时域显式递推表达式（17）的推导，可得方程（19）在各时刻动力响应的递推表达式为

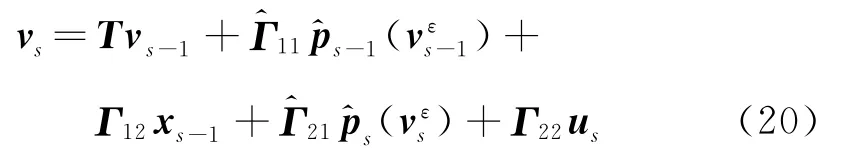
式中

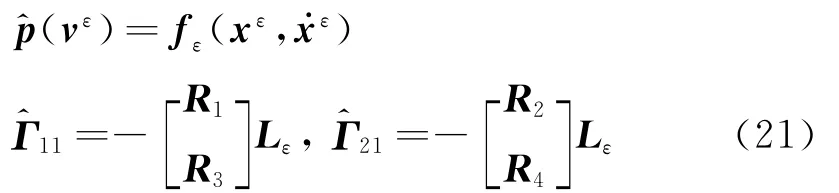
重复迭代式（20）可得所有预测时刻的动力响应为

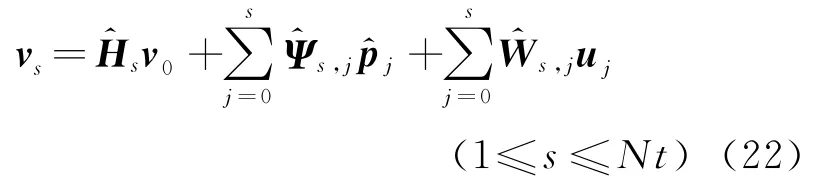
式中 各系数矩阵依次为

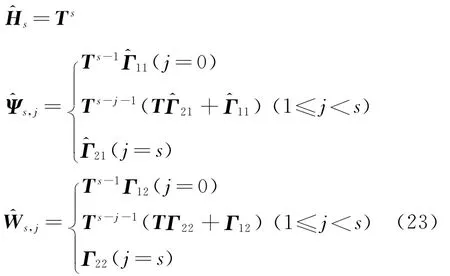
由于在实际工程中，只能获取有限的状态测量反馈信息，因此本文假设控制器设计的输出方程为

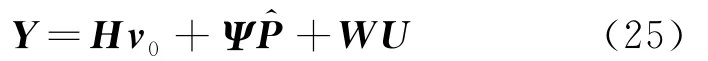
式中 系数矩阵Ψ和W只与线性结构参数和定位矩阵有关，且仅需计算前两列，后续各列由第二列赋值与组装即可获得。另外，在式（25）中（1≤s≤Nt）为预测的各时刻结构局部非线性等效外力，相比于各预测时刻的初始状态v0和控制力U，其对输出状态向量Y的影响相对较弱，不妨借鉴模型线性化思想对非线性环节进行处理，假设＝＝…＝，从而Y为变量U的函数。

取性能指标为

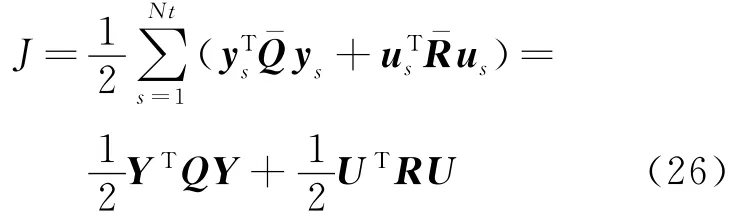
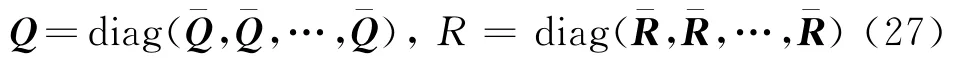
为使得性能指标J取极小，则

将式（25）代入式（26），由式（28）可得控制力U 为

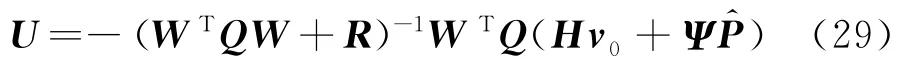
取U的初始时刻控制力u0做为当前时刻的最优控制力，进而通过求解局部非线性动力学方程（1），便可求得当前时刻的受控动力响应。如此随时间步进，不断滚动计算，即可完成该局部非线性结构振动控制问题的数值仿真。

综上所述，表1给出了本文考虑局部非线性结构振动模型预测控制的算法流程。

需要指出的是，各时间步所预测的最优控制力U中（即式（29）），包含预测初始状态量v0，在获取v0时，为避免直接对非线性动力学方程所有维度完全迭代求解。

4 局部非线性结构动力学的时域显式降维迭代

当系统的初始状态v0等于0向量时，由式（17）可建立各时刻结构响应显式表达式为

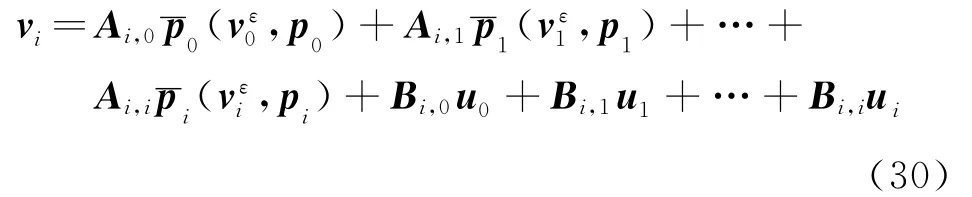
式中 系 数 矩 阵 Ai，0，Ai，1，…，Ai，i和 Bi，0，Bi，1，…，Bi，i仅与线性结构参数和定位矩阵有关，分别反映了各时刻外激励和控制力对当前时刻结构动力响应的影响。各时刻的系数矩阵Ai，k和Bi，k列入表2和表3。

表1 局部非线性结构振动模型预测控制算法流程Tab．1 Implementation of the MPC method for the local nonlinear structural vibration

表2 各时刻的系数矩阵ATab．2 Coefficient matrices Afor each time instant

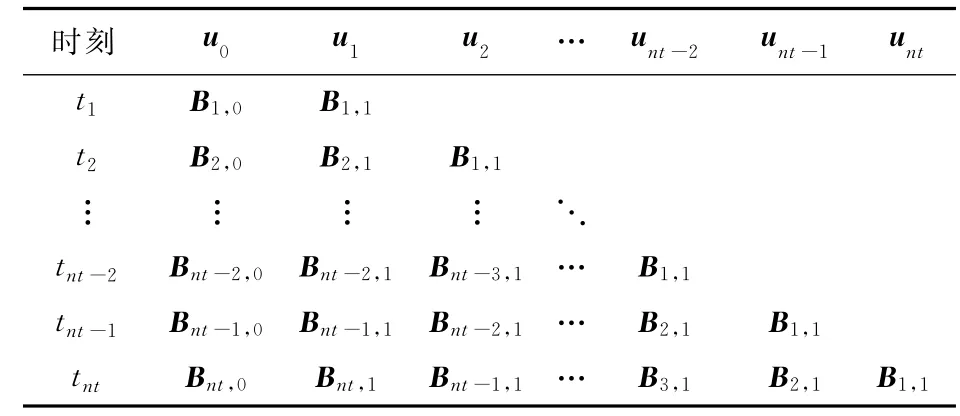
表3 各时刻的系数矩阵BTab．3 Coefficient matrices Bfor each time instant

由表2和表3可知，只需要分别计算系数矩阵A和B的前两列，而后续的各列由第二列赋值组装即可。从而，系数矩阵的所有元素并不需要全部存储，仅需要保存相应的前两列即可，很大程度上降低了本算法的内存需求。

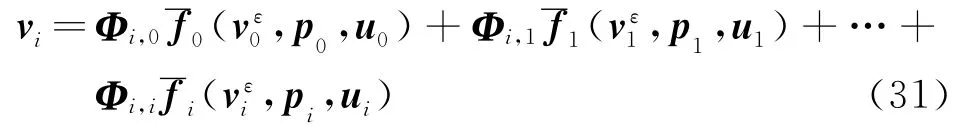
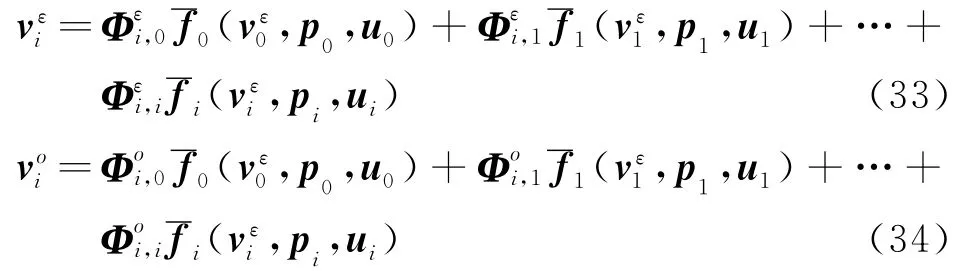
5 数值算例验证与讨论

通过两个数值算例，来验证和讨论所提考虑局部非线性结构振动的模型预测控制算法的正确性和有效性。需要说明的是，本文所有算例仿真均在个人计算机（主要参数为Intel（R）core（TM）i7－4800MQ （2．70GHz）processor and 8GB RAM，running on Windows7 64bit）的 MatlabR2014a环境下执行。

5．1 局部非线性弹簧振子动力系统

如图1所示，质量m1＝m2＝m3＝250kg，线性弹簧刚度k1＝k2＝k3＝1000（N／m），质量块m1与m2之间安置了非线性弹簧ks，恢复力Fs＝2×104（Δx）3，Δx为弹簧ks两端点相对位移。假设系统结构阻尼为瑞利阻尼（参数ξ＝0．02，ζ＝0．03），分别采用ANSYS和时域显式降维迭代方法对其在简谐支承位移（加速度x¨g（t）＝0．5sin（2πt）（m·s－2））作用下进行无控振动响应时程分析。

仿真结果对比如图2所示。其中，图2（a）为3号质量块的位移时程曲线，图2（b）为局部非线性弹簧ks的恢复力时程曲线。可以看出，ANSYS时程分析与时域显式降维迭代法的求解结果几乎一致，说明本文采用的考虑局部非线性动力学时程分析方法正确。

5．2 含粘滞阻尼器的毗邻框架结构振动控制系统

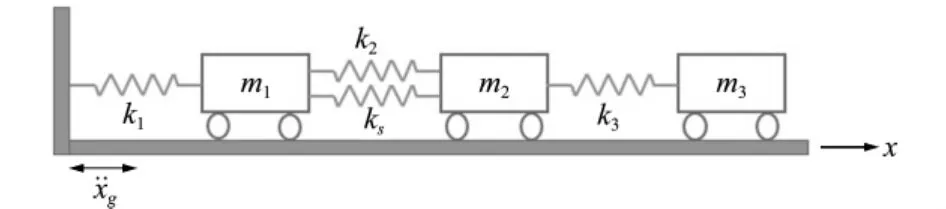
图1 局部非线性弹簧振子系统Fig．1 Local nonlinear mass－spring system

如图3所示，考虑某局部安置了粘滞阻尼器的毗邻框架建筑结构，作动器安装在各楼层右端点（圆点），观测点为各楼层的左端点（方点），并假定在部分楼层局部装有粘滞阻尼器。采用有限元方法建立模型，梁、柱以及毗邻建筑的连接均使用平面梁单元，结构总自由度为360，并假定结构的阻尼为瑞利阻尼。模型的材料与几何参数列入表4，而粘滞阻尼器的非线性阻尼力模型［15］为

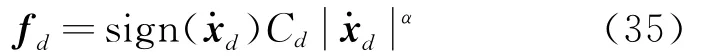
图2 动力学时程分析的结果对比Fig．2 Comparison of the results for the dynamic analysis

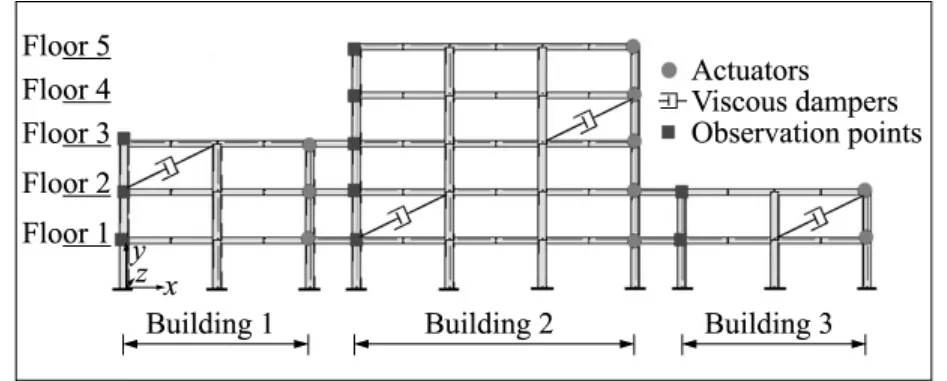
图3 局部安置粘滞阻尼器的毗邻框架结构Fig．3 Adjacent frame structure with viscous dampers installed locally

表4 模型的几何与材料参数Tab．4 Geometry and material parameters

p阵；取预测步长和采样步长一样，同为0．02s，预测时间为1s，仿真总时间为15s。基于本文所提局部非线性结构振动模型预测控制算法，讨论结构在EI Centro地震激励作用下其水平方向上的振动控制。

如图4所示，考察在有控情况下，粘滞阻尼器带来的局部非线性对控制结果的影响。其中，图4（a）为毗邻框架结构最高层位移时程曲线，图4（b）为对应最高层处作动器输入的控制力时程曲线。

从图4（a）可以看出，在无控时，由于粘滞阻尼器的作用，结构位移响应已有所降低。绝对位移峰值由0．4212m降低为0．2648m，降低了37．13%。在有控时，若控制设计时不考虑局部非线性因素，绝对位移峰值为0．0467m；若控制设计时考虑局部非线性因素，则绝对位移峰值为0．0358m，降低了23．34%。从图4（b）可以看出，有控时需要提供的控制力大部分时刻与无控时一致，仅在局部时刻略微增大，这说明在设计控制器时，考虑结构局部非线性因素，可取得更令人满意的控制效果。

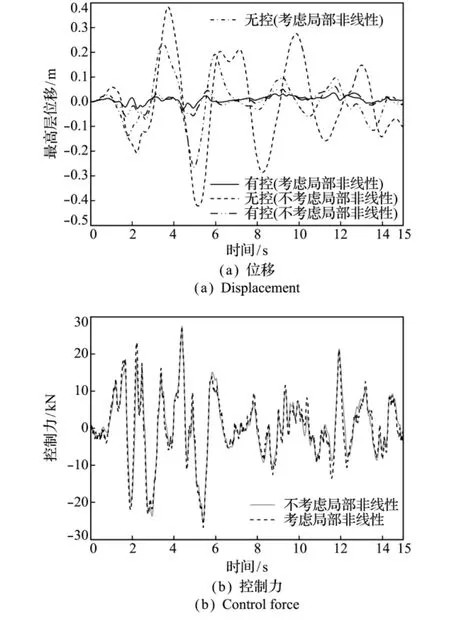
图4 局部非线性因素对结构振动控制的影响Fig．4 Impact of the local nonlinear factors on the results for structural vibration control

综上所述，考虑局部非线性结构振动模型预测控制算法正确且有效，很好地抑制了这类局部非线性结构在地震等作用下的振动响应。

6 结 论

本文提出考虑局部非线性结构振动的模型预测控制算法，为求解大型复杂局部非线性结构振动控制问题提供了一种有效的主动控制策略。首先，通过Newmark－β法，推导了局部非线性结构动力响应的时域显式递推表达式；然后，在该表达式的基础上，基于模型预测控制理论，建立局部非线性结构振动的预测模型，并借鉴模型线性化思想对非线性环节进行处理，提出了考虑局部非线性结构振动的模型预测控制算法；最后，利用局部非线性结构动力学时域显式表达式优势，给出了非线性动力方程的时域显式降维迭代策略，以此提高了算法的在线计算效率，从而完成整个控制过程。数值算例表明，所提算法求解正确，且在设计控制器时，考虑粘滞阻尼器等类似的结构局部非线性因素，能更加高效地抑制结构的振动响应。