结构优化半解析灵敏度分析的改进算法

陈飙松， 张力丹， 鲁一南， 程耿东

（1．大连理工大学 工业装备结构分析国家重点实验室，大连116024；2．大连理工大学 江苏研究院，常州213164）

1 引 言

高效的灵敏度分析是提高优化效率的关键［1］，已有的灵敏度求解方法包括全局差分法、解析法与半解析法。全局差分法［2］只要求有限元程序提供相邻设计的结构性能，不牵涉这些设计的有限元模型和性能的计算方法和程序细节，可把有限元软件作为黑箱，十分简单，但每做一次敏度分析，针对n个设计变量要做n＋1次完整结构分析，效率很低［3］。解析法［4，5］通过推导得到灵敏度公式，计算效率和精度都较高，但推导这些公式并编程通常复杂且困难，尤其在形状优化中，形状设计变量与有限元单元列式的关系不仅复杂而且依赖于单元类型，推导和编程均不具通用性［6］，不仅给程序开发造成困难，同时对于单元丰富的商用有限元程序，用户也无法进行二次开发［7］。为此，程耿东等［8］提出了半解析灵敏度分析方法，为将有限元和结构优化高效结合提供了途径。该方法通用性强，效率高，广泛地应用于多种结构优化问题中。如Kiendl等［9］将半解析灵敏度分析方法及敏度加权应用于壳结构的等几何形状优化分析中；陈敏等［10］在山地车车架结构的轻量化设计上使用了半解析灵敏度分析方法。传统半解析灵敏度分析方法基于单元级别，需提取摄动前后两组单元矩阵，影响计算精度和效率。

因此，本文对算法提出如下改进。（1）从总体角度考虑半解析灵敏度分析公式的计算方法，避免了摄动前单元刚度阵和质量阵等的提取，减少编程工作量和节省矩阵读取时间的同时，减少了舍入误差。（2）将算法推广到应力、自振频率、屈曲临界荷载以及瞬态响应等力学量的灵敏度计算。以梁单元与壳单元为例，构建测试算例。结果表明，该方法可适用于多种分析类型，设计变量步长有更大的数值稳定区域，可为采用非结构化网格建模结构的形状优化提供新途径。（3）从总体角度推导的半解析灵敏度公式，在结合自主有限元程序与商用有限元程序进行实现时均具有较大优势。本文的公式推导以及所组织的算例测试主要针对基于自主有限元程序的半解析灵敏度分析方法，同时给出此方法结合商用软件的应用，值得说明的是，对于静力灵敏度问题，结合商用软件使用时，无需提取任何矩阵。

2 传统半解析灵敏度分析方法

半解析灵敏度方法将荷载和刚度阵等对于设计变量的导数用差分替代。静力问题位移灵敏度分析公式为

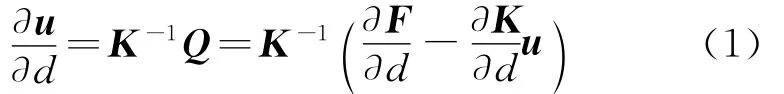
式中u为结构整体位移向量，d为设计变量，F为施加在结构上的外荷载，K为结构总刚，Q为拟荷载向量。对于荷载与设计变量无关的情况，拟荷载可表示为

其中Ke为单元刚度矩阵，ue为单元位移向量。

对于静力问题，式（2）需要提取摄动前后两组单元刚度矩阵，再进行差分求解；而对于特征值问题，还需提取两组单元质量阵或几何刚度阵，从而增加编程工作量和数据输入／输出的工作量。在结合现有的商用软件进行半解析灵敏度分析时，从软件读出的单元刚度阵往往只有固定位数的有效数字，按上述方法计算时有效位数有时会损失很多，严重影响计算精度。

3 改进半解析灵敏度分析方法

3．1 静力问题

将传统方法进行改进设计，使其程序实现过程更为简便，首先对静力问题进行推导。从总体角度考虑静力问题位移灵敏度求解。对于结构的静力分析问题：

结构位移的半解析法灵敏度分析公式如下，

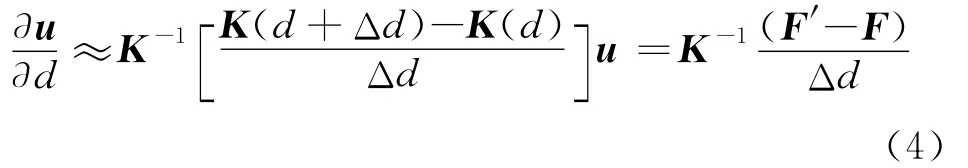
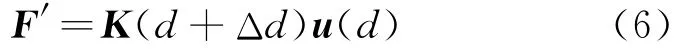
由式（5）可知，F为外荷载。式（4～6）直接基于总刚进行求解，更适用于单刚提取困难、提取精度较低且提取过程耗时的商用有限元程序。在基于自主有限元程序进行半解析灵敏度分析时，因单刚较易获得，可将式（6）进行如下改进，即F′分解为单元一级进行计算并累加于总体，从而避免总刚的集成。

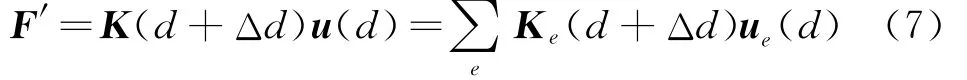
该方法从总体角度入手，在基于自主有限元程序进行实现时，使用改进公式（4～7），避免初始刚度矩阵的提取，以及总体刚度阵的集成，并可减小刚度矩阵相近数值相减造成的有效数字损失；在结合商用软件实现时，使用总体公式（4～6），F′的计算可将初始所有节点的位移u作为结构的位移全约束，通过商用软件提取外荷载得到，从而无需读出任何刚度阵，同时也避免了单元刚度矩阵读取的有效数字位数对计算精度的影响。

在得到静力位移灵敏度的条件下，还可将其应用于静应力灵敏度的求解，结构的应力为

其基于总体的半解析灵敏度方法的计算可以近似为

式中 D为整体弹性矩阵，B为整体应变矩阵，u为整体结构位移，d为设计变量，将位移乘入即可得到

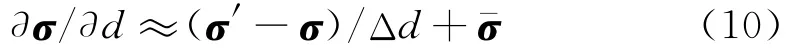
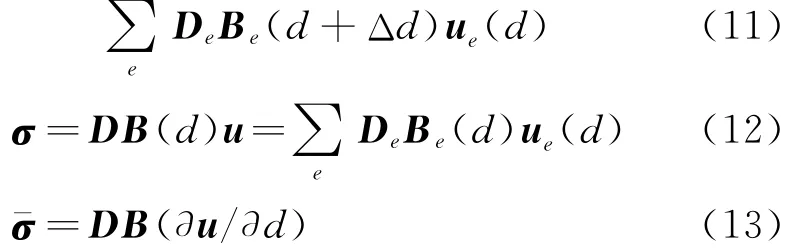
其中，De为单元弹性矩阵，Be为单元应变矩阵，ue为单元位移，由式（12）可知，σ为初始结构的应力。根据式（10），改进方法计算静应力灵敏度时，无需提取原设计的单元弹性矩阵与单元应变矩阵，而用初始应力代替。基于自主有限元程序进行的半解析灵敏度分析，σ′的计算可先形成摄动后的De·Be（d＋Δd），将摄动前的结构位移分解到单元上，代入摄动后的应力求解流程中，对于σ－的计算，可先求解出位移相对于设计变量的灵敏度，再将其作为结构位移并分解到单元上回代于摄动前的应力计算流程，得到的应力即为σ－。在结合商用软件使用时，可将初始结构位移及求得的位移灵敏度分别作为结构的位移约束，通过商用有限元软件直接计算应力得到σ′与σ－，无需提取任何矩阵。

3．2 特征值问题

对于自振分析非重特征值灵敏度问题［11］，基于总体的半解析式为

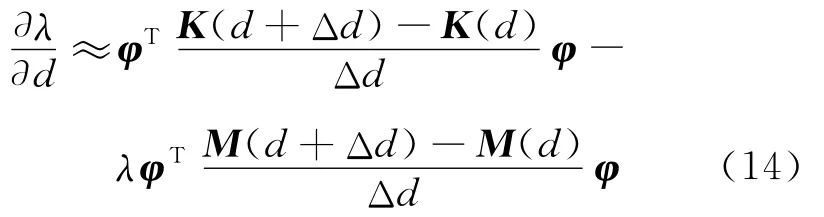
将总体特征向量乘入可得

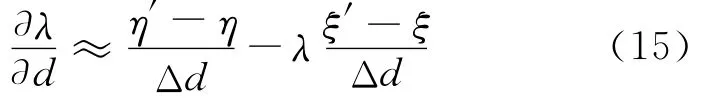
将式（28）改写为总体差分格式，并将加速度、速度及位移乘入差分近似的公式中，可得到f－为

考虑自振分析的特性，对质量阵归一化：

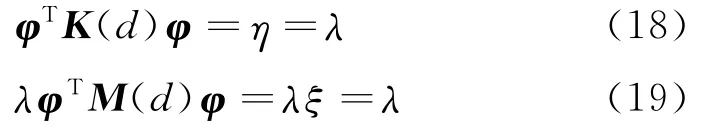
则有

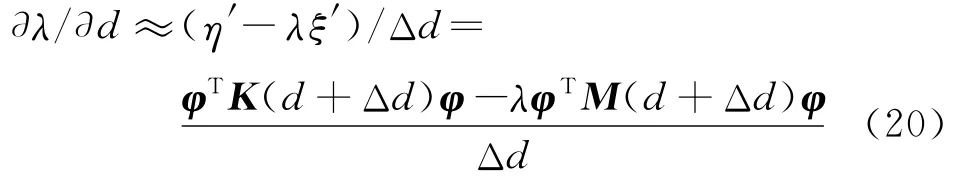
式（20）更适用于总刚读取效率高于单刚的商用有限元软件。基于自主有限元程序进行半解析灵敏度分析时，为避免总体矩阵的集成，可将式（16，17）进行如下改进，

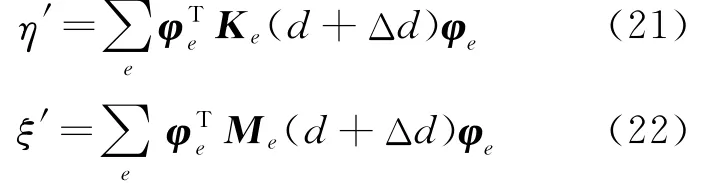
则式（20）可写为

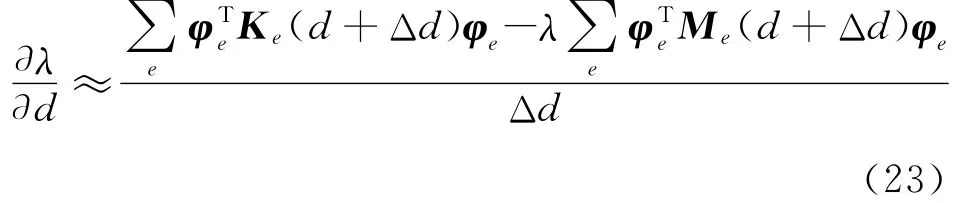
同理，对于屈曲分析非重特征值灵敏度问题［12］可得

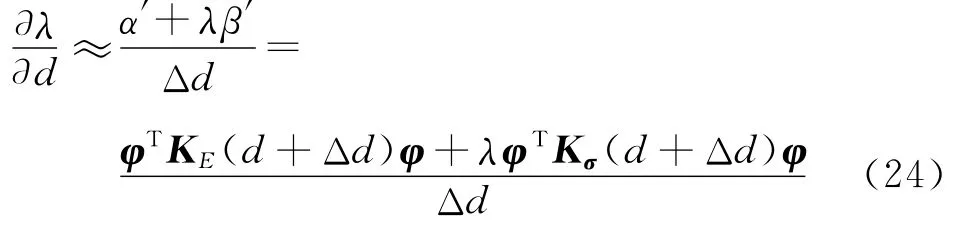
以及

3．3 瞬态问题

瞬态响应方程［13］的表达式为Mu¨＋Cu·＋Ku＝f（t） （26）式中 M为总体质量阵，C为总体阻尼阵，K为总体刚度矩阵，u¨为总体加速度，u·为总体速度，u为总体位移，f（t）为施加在结构上的时变荷载，对于荷载与设计变量无关的情况，瞬态问题灵敏度求解公式［14］为

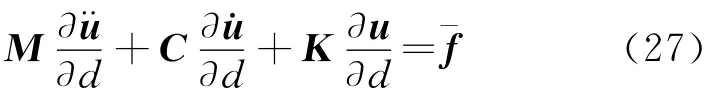
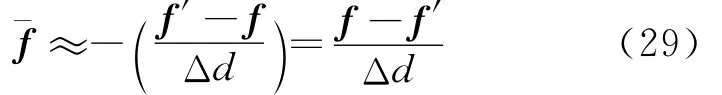
其中，

由式（31），f为施加在结构上的时变荷载，即瞬态问题半解析法公式的右端项可写为

在计算过程中，先计算式（27）的右端项f－，并将其作为新的时变载荷，代入瞬态问题求解方法［15］中，如 NewMark法［16］和 Willson－θ 法［17］等，求解初值为0的瞬态问题，得到的位移、速度和加速度值即为结构的位移、速度和加速度灵敏度值。

4 算例测试

4．1 测试模型

现构建两种有限元模型，对静力分析的位移、应力灵敏度、自振分析特征值灵敏度以及瞬态分析位移灵敏度进行算例测试。如图1所示，框架尺寸h＝6m，b＝4m，梁矩形截面为0．15m×0．06m，弹性模量E＝2×1011Pa，泊松比ν＝0．3，密度ρ＝7．8×103kg／m3。采用欧拉伯努利梁单元进行建模。每段梁结构划分20个梁单元，共300个梁单元。该模型用于以下分析类型。

（1）静位移。底部固定，在其顶部左端施加沿x轴正方向大小为0．1N的集中荷载，取顶部右端点x方向位移对于b的灵敏度，

（2）静应力。边界条件同静位移，取左侧柱根部单元高斯点最大应力对于b的灵敏度。

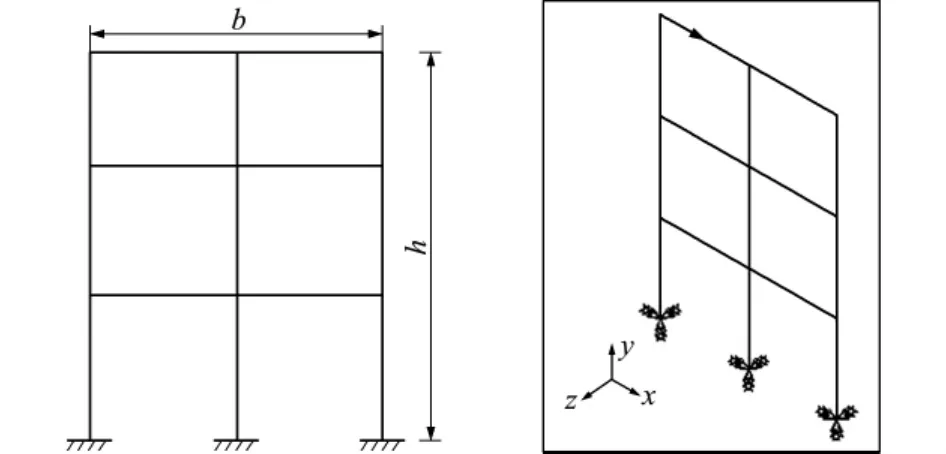
图1 框架模型Fig．1 Model of frame

（3）自振。底部固定，取基频对于b的灵敏度。

（4）瞬态。底部固定，荷载位置与方向同静位移，取顶部右端点x方向对于b的灵敏度。

如图2所示，椭球壳结构，长轴a＝4m，短轴b＝3m，弹性模量E ＝2×1011Pa，泊松比ν＝0．3，密度ρ＝7．8×103kg／m3。采用柯西霍夫理论四边形壳单元进行建模，网格剖分如图2所示，共300个单元。该模型将用于以下分析类型。

（1）静位移。底部固定，在其球壳顶部中央节点，施加沿z轴负方向大小为0．1N的集中荷载，取顶部z方向位移对于b的灵敏度。

（2）静应力。边界条件同静位移，取顶部单元高斯点最大应力对于b的灵敏度。

（3）自振。底部固定，取基频对于b的灵敏度。

（4）瞬态。施加于结构上的荷载位置与方向同静位移，取顶部z方向位移对于b的灵敏度。

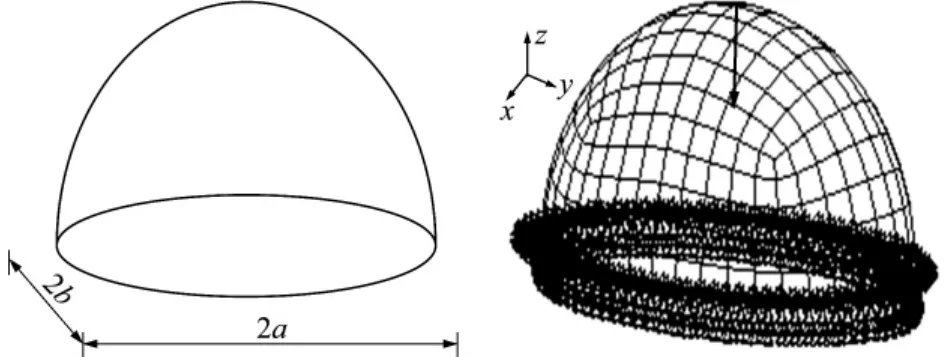
图2 椭球壳模型Fig．2 Model of elliptical shell

4．2 测试结果

基于文献［3］对于相对灵敏度的定义，设全局差分法稳定值为ΔF0GFD，分别定义GFD方法、SA方法与MSA方法的相对灵敏度为

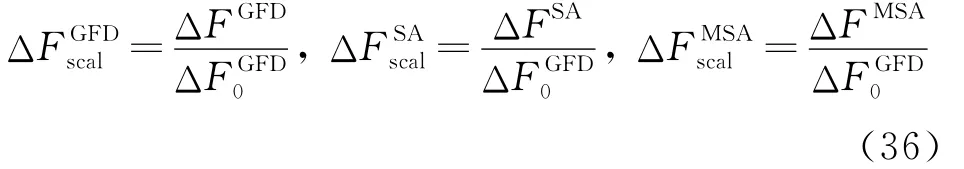
其符号说明如下，

GFD（global finite difference）为全局差分法；

SA（semi－analysis）为将单元刚度阵直接进行差分的传统半解析方法；

MSA（modified semi－analysis）为基于总体的改进半解析方法，此处采用自主有限元程序进行实现（摄动后部分采用单元一级累加于总体，避免总体矩阵的集成）。

图3～图6分别为静位移、静应力、自振特征值和瞬态位移的相对灵敏度随摄动步长与设计变量之比的负对数δ＝－log（ΔL／L）的变化规律。梁单元建模的框架结构（简称梁结构）测试结果绘于图（a），用表示。壳单元建模的板壳结构（简称板壳结构）测试结果绘于图（b），用表示。

从四种灵敏度分析结果可以看出，半解析方法（MSA与SA）在梁结构静应力灵敏度的求解上，数值稳定性较为突出，如图4（a）所示，GFD稳定范围为1e－4～1e－7，SA方法为1e－5～1e－10，MSA方法为1e－5～1e－11。与SA相比，MSA方法具有较长的数值稳定区间，但无法缩小有限单元刚体转动造成的误差［17］，因此不适用于大摄动步长。

从梁结构与板壳结构（非类梁结构）的结果对比可以看出，对于板壳结构，三种方法的数值稳定范围均较长且差异不大，而对于梁结构，三者具有较大差别。从整体趋势来看，GFD法的稳定值出现于大摄动步长，而对于SA或MSA方法，则在较小摄动步长达到稳定，尤其对于MSA方法，缓解了相近数值相减造成的误差，在步长更小的位置仍能保证数值精度。对于形状设计变量问题，该特性能保证摄动前后网格的一致性，对于优化迭代计算较为有利。

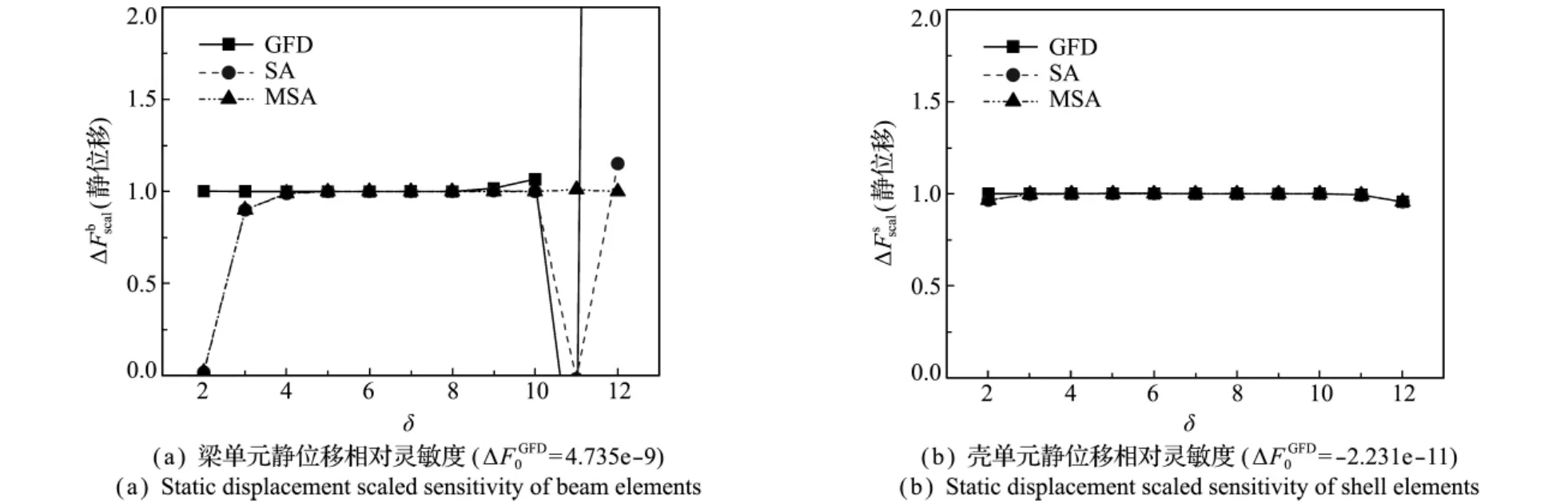
图3 静力位移相对灵敏度随摄动步长的变化Fig．3 Static displacement scaled sensitivity fluctuated with the perturbation step length

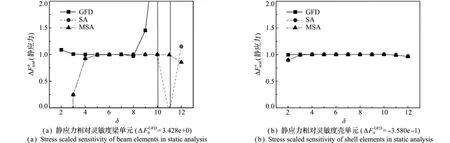
图4 静应力相对灵敏度随摄动步长的变化Fig．4 Static stress scaled sensitivity fluctuated with the perturbation step length

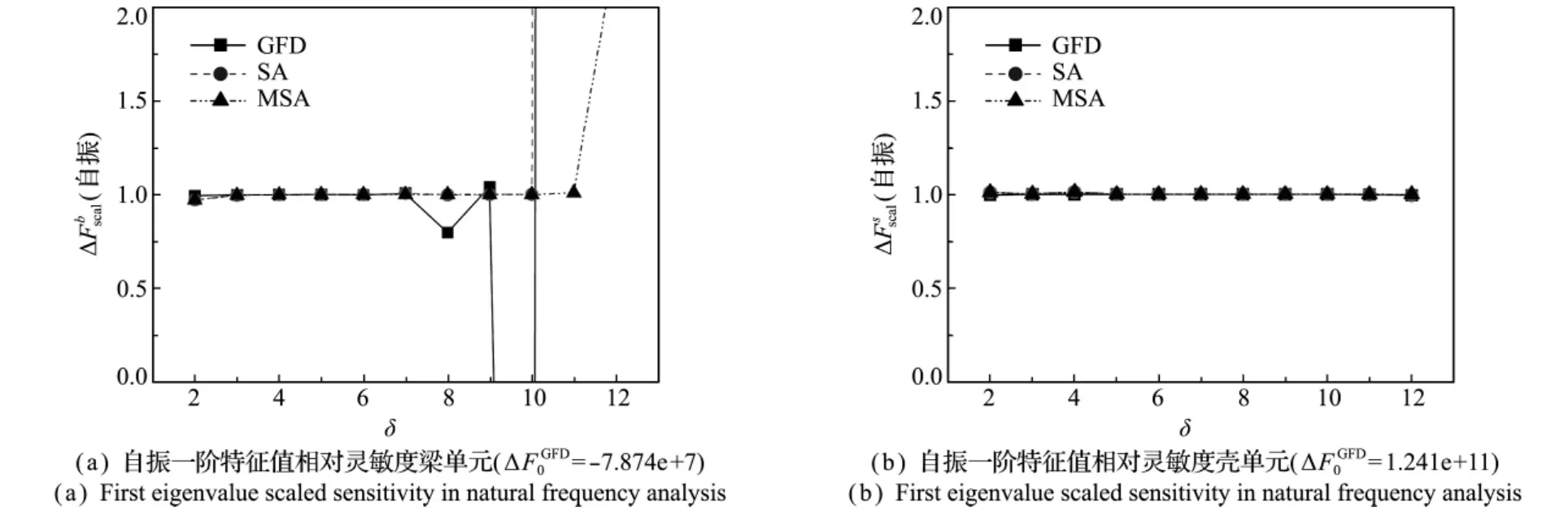
图5 自振特征值相对灵敏度随摄动步长的变化Fig．5 Eigenvalue scaled sensitivity of natural frequency analysis fluctuated with the perturbation step length

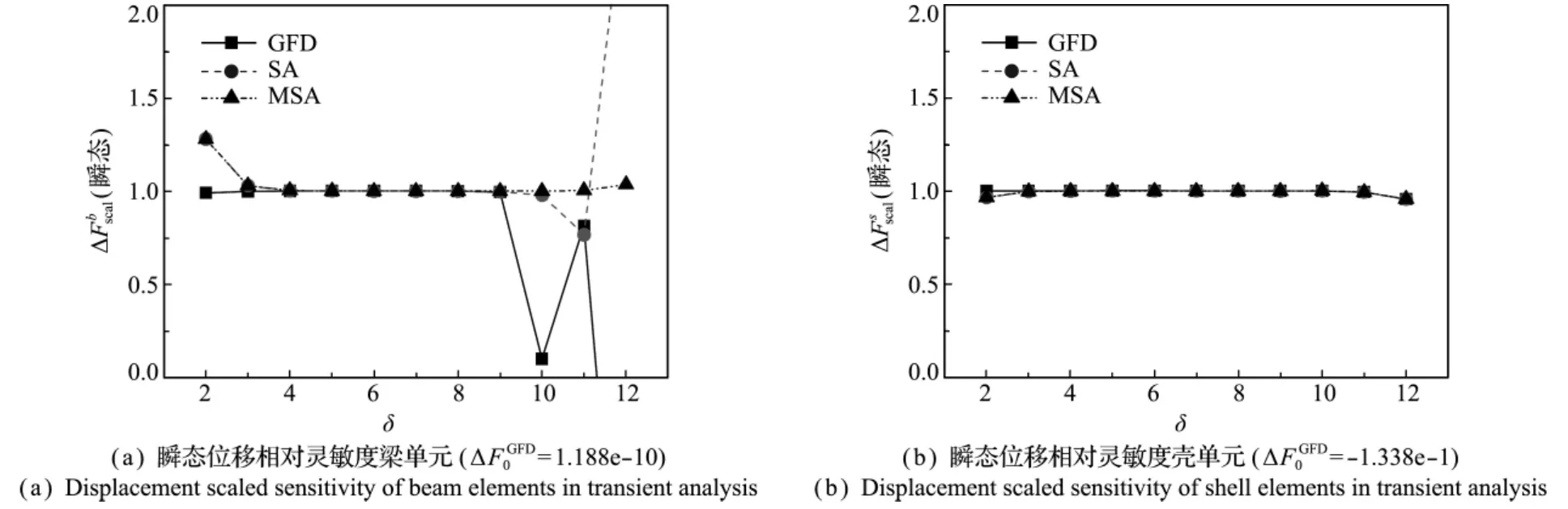
图6 瞬态位移相对灵敏度随摄动步长的变化Fig．6 Displacement scaled sensitivity of transient analysis fluctuated with the perturbation step length

5 结 论

（1）本文将传统基于单元级别的灵敏度求解公式转为结构层次进行考虑，得到无需提取初矩阵的程序实现方法。

（2）在静力问题测试的基础上，将半解析方法应用于自振和瞬态分析等多种分析类型，测试算例表明，该方法在多种分析类型上都可以得到针对摄动步长较大的稳定区域。

（3）测试算例为改进方法在自主有限元程序上的应用。对于结合商用有限元软件进行灵敏度分析，应将摄动后部分直接在结构层次上进行求解。相较传统读出摄动前后两组单刚的方法，在很大程度上降低了矩阵读取时间，提高了总体计算效率，且能避免商用软件提供的单刚具有较少有效数字位数对计算精度造成的严重影响。