DMC-PID串级控制在拖轮动力定位系统中的应用

杨奕飞，吴艳艳，谈敏佳

(江苏科技大学 电子信息学院，江苏 镇江212003)

0 引言

船舶动力定位系统[1-2](dynamic positioning system)，指的是船舶利用自带的推进器等装置产生推力以抵御风、浪、流等外界环境干扰力对船产生的干扰，从而使船舶保持在某一固定位置或沿预设航向航行的系统。

拖轮在海上航行或进行拖曳作业时，往往会受到复杂多变的海上环境的影响，即风、浪、流等外界环境的干扰，这些都会对拖轮航行的航向和定位产生相当大的影响。

动态矩阵控制[3-4](DMC)是典型的预测控制算法其中的一种，近年来被广泛应用于控制领域。DMC算法是基于系统阶跃响应的控制算法，它适用于带有纯滞后环节的线性对象，且对大惯性系统的适应能力强，因而该算法的鲁棒性和跟踪性较好。然而，动态矩阵控制应用于控制系统，其抗干扰能力很差，且拖轮在海上航行要面对各式各样的环境干扰，因而在运用动态矩阵(DMC)的过程中引入了具有强抗干扰能力的PID控制，即DMC-PID串级控制。把DMC控制和PID控制相结合，这种控制算法既有很好的抗干扰能力，又有良好的稳定性和鲁棒性。目前， DMC-PID串级控制已被广泛应用于化工、温控等领域[5]，且控制效果良好，但其在动力定位中的应用极少。本文将DMC-PID串级控制应用于动力定位系统，具有一定的创新性。

1 系统运动模型

拖轮在海上运动的数学模型主要由两部分组成：高频运动模型和低频运动模型。由于拖轮高频运动仅仅造成船体的上下振荡，不会影响拖轮的位置变化，因而本文拖轮的运动只考虑低频运动，即拖轮在纵荡、橫荡、艏摇3个自由度上的运动。

拖轮低速船舶运动模型[6-7]如式(1)所示。

(1)

2 环境干扰力模型

拖轮在海上进行拖曳作业时往往会受到风、浪、流等外界环境作用力的干扰，使得拖轮的位置和艏向发生变化。

2.1 风的模型

设ρa为空气密度，则风作用在拖轮上的风力和风力矩计算公式[8]如式(2)所示。

(2)

式中：Vw为相对风速；AT、AL分别为上层建筑正投影和侧投影面积；L为拖轮总长；Cdx、Cdy、Cdn分别为纵荡、橫荡方向的风力系数和艏摇方向的风力矩系数。

2.2 流的模型

一般情况下，流载荷的计算方法和风载荷类似，其计算公式可以表示为:

(3)

式中：Vc为流速；ST、SL分别为拖轮水线下的正投影和侧投影面积；L为拖轮总长；Ccx、Ccy、Ccn分别为纵向、横向方向的流力系数和艏摇方向的流力矩系数。

2.3 二阶波浪力模型

拖轮在海上作业时所受的海浪干扰可分为两部分：一阶波浪力和二阶波浪力。本文主要是研究拖轮的低频运动，高频部分则通过滤波方式滤除，这里将不再考虑一阶波浪力。

考虑到波浪对船舶操纵性能的影响，Daidola提出了下列波浪漂移力和力矩的计算公式：

(4)

式中：Lw为船舶水线长；a为波浪的平均幅值；Cxw、Cyw、Cnw为纵向、横向、艏摇3个方向的实验系数，λ为船舶与波浪的遭遇角。

3 控制算法及控制系统结构设计

3.1 动态矩阵控制

1)预测模型

预测模型为:

(5)

其中，A为系统的动态响应矩阵，P为预测时域，M为控制时域。

2) 滚动优化

DMC是一种以优化确定控制策略的算法。采样时刻t=kT的优化性能指标可取为：

(6)

3) 反馈校正

预测误差：

e(k)=r(k)-y(k)

(7)

校正后的预测输出为：

(8)

参考轨迹柔化后的轨迹：

(9)

式中i=1,…,P。

系统校正后的预测值作为系统下一时刻的预测初值，移位过程如式(10)：

(10)

3.2 DMC-PID串级控制系统

针对拖轮，本文提出了将动态矩阵控制和PID控制相结合的串级控制算法，它的系统控制框图如图1所示。

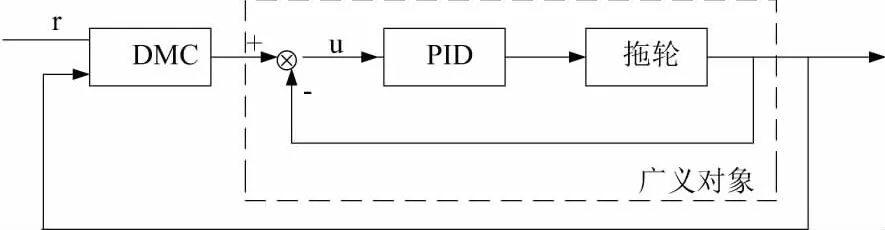
图1 DMC-PID串级控制结构

DMC-PID[9-10]串级控制是指在内环控制回路中采用传统的PID控制，外环回路采用动态矩阵控制(DMC)。内层采用PID控制，这一层控制采用了比DMC控制高得多的频率，其目的在于快速有效地抑制外界风、浪、流等环境的干扰。这一被控回路可视为一个广义对象。在外层，再用DMC对这一广义对象进行控制[9]，以保证系统具有良好的鲁棒性。这种DMC-PID串级控制兼具了PID控制的强抗扰能力和动态矩阵控制良好的鲁棒性和动态性。

3.3 参数选择

对于拖轮，控制算法中参数取值不同时，其控制效果也会发生变化。在仿真研究过程中，总结出以下几条参数整定的规律：

1) 采样周期T和模型长度N：T和N的选择尽可能完整地包含对象的动态信息。从计算机的计算需求和内存角度出发，应当选择适当的采样周期T以便模型维数保持在20～50。

2) 预测时域P：在覆盖拖轮阶跃响应主要动态信息的前提下，P的取值越小，系统的快速性越好；P取值越大，系统的稳定性越好。

3) 控制时域M：M值越小，控制系统跟踪性能越差；M值越大，系统的稳定性变差。

4) 误差权系数qr：与P的取值相对应，时滞部分qr=0，剩下部分取1。

5) 控制权系数ri的主要作用在于防止控制增量发生剧烈变化。参数整定时，可先设置ri=0；若控制量变化剧烈，可略加大ri，实际上，ri只取一个较小的值就能使控制量变化趋于平缓。

6) 柔化因子α：α越小，拖轮的抗干扰性越差，鲁棒性越好(0<α≤1)。

4 系统仿真研究

以拖轮为例，用MATLAB软件对其控制系统进行仿真研究。拖轮的相关参数[10]见表1。

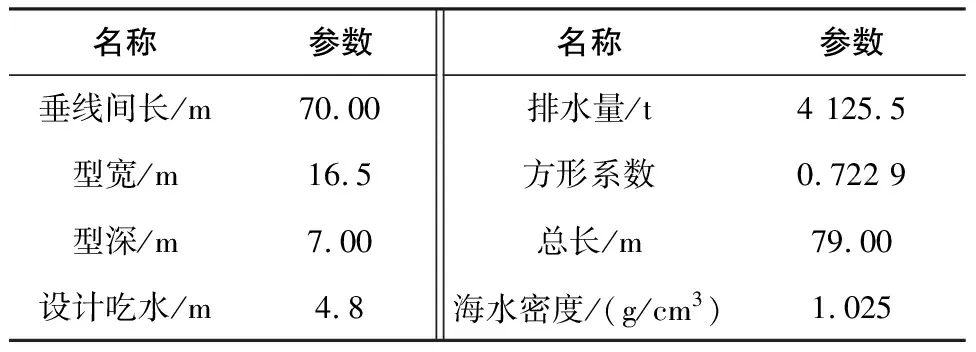
表1 拖轮相关参数表

通过经验公式估算得到式(1)中的参数矩阵为：

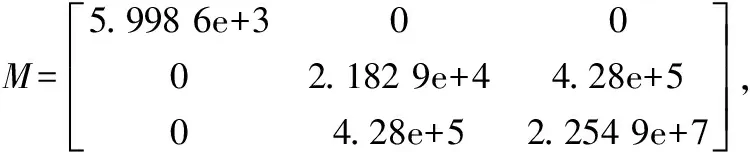
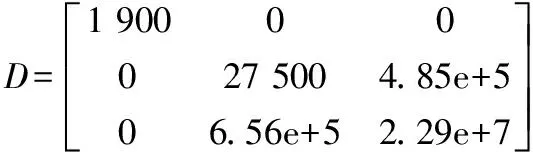
DMC-PID串级控制和PID控制下纵荡方向的仿真图如图2。

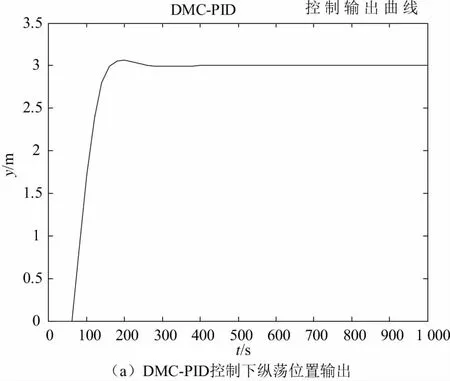
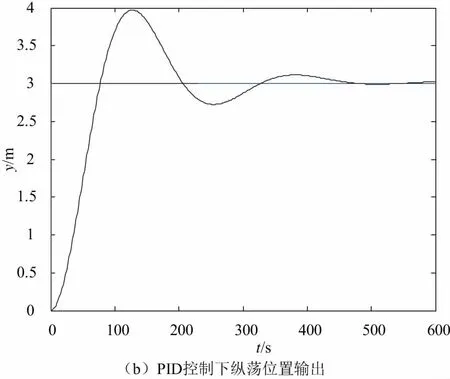
图2 DMC-PID串级控制和PID控制下纵荡位置输出

在t=600s处，给系统加一个d=1的外界干扰，DMC-PID串级控制和PID控制下纵荡方向仿真图如图3。

对比仿真结果，图2中两幅图可知，DMC-PID串级控制算法的控制效果更好。对比仿真结果，不难发现：在PID、DMC-PID控制下，系统到达稳态值的时间分别约为250 s、450 s。从系统超调角度考虑，DMC-PID串级控制下的系统基本实现无超调，而PID控制下的系统超调量较大，系统跟踪性不是很好。对比图3中两幅图，干扰情况下，PID、DMC-PID串级控制下系统恢复到稳定状态的时间分别为200 s、350 s，显然DMC-PID串级控制下系统的抗干扰能力更好。综上所述，结合快速性、稳定性和抗干扰能力，DMC-PID串级控制的控制效果更好。

5 结语

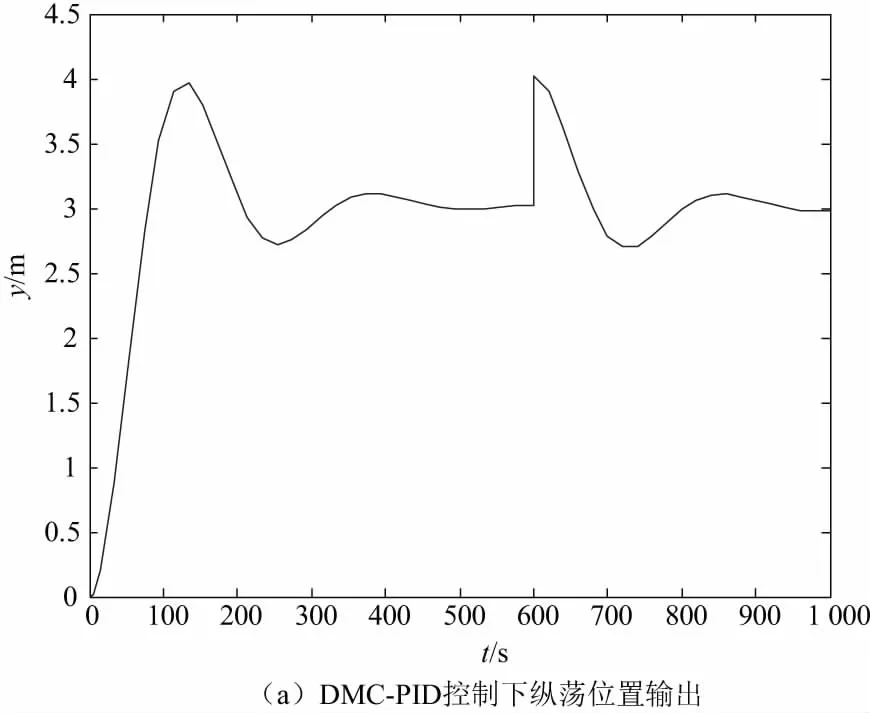
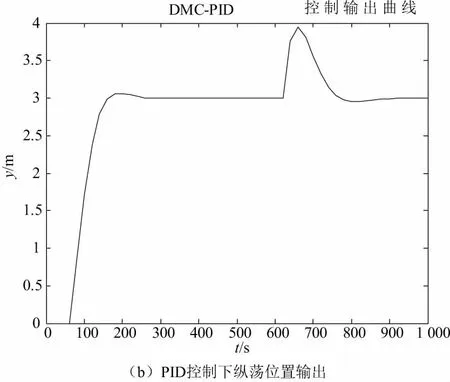
图3 干扰情况下纵荡位置输出

以天航拖轮为控制对象，提出了DMC-PID串级控制算法，并且设计了相应的控制系统，且对其控制效果进行了仿真研究，并与传统PID控制的仿真结果进行了对比分析，结果表明：

1) 在相同条件下，多功能拖轮在DMC-PID控制下的控制效果更好，不仅提高了系统的快速性，且跟踪性和稳定性较好。

2) 在给系统加相同的外界干扰的情况下，与传统PID控制相比，DMC-PID控制下系统具有更强的抗干扰能力。

3) DMC-PID串级控制能提高系统的快速性和稳定性，且具有较强的抗干扰能力，从而有效地提高了拖轮的动力定位能力。