四旋翼飞行器航迹规划和控制研究
王彪,周杰,孔大庆,唐超颖
(南京航空航天大学 自动化学院,江苏 南京 211106)
0 引言
四旋翼无人机是一种由四个旋翼驱动的飞行器,与单旋翼直升机相比,具有体积小、成本低、维护和操作简单等优点。因此非常适合在城市低空、狭窄街道以及室内完成高难度、高危险的任务[1]。由于室内环境复杂,能够提供的飞行空间有限,因此需要以平滑且曲折度低的较优路径躲避障碍物,确保安全、快速地到达终点。
RRT路径规划算法在无障碍的空间内进行采样,以逐级递增的方式生成一颗连接起点和目标点的搜索树。该算法不需要启发函数,具有很强的搜索倾向,适用于小型四旋翼飞行器的室内航迹规划问题[2]。因此本文采用RRT算法规划航迹,进而考虑四旋翼飞行器的非线性运动特性,很多国内外研究人员提出了多种基于非线性控制方法的控制器,如H无穷控制[3]、反演控制[4]、滑膜控制[5]、自适应控制[6]等等,以提高四旋翼飞行器的运动性能。可是非线性控制器的结构复杂,工程可行性较低,而当四旋翼飞行器处于低速巡航模式时,姿态运动和质心运动各通道近似解耦,可用传递函数来描述其输入输出特性,因此可基于六自由度通道的传递函数模型进行航迹和航姿控制器的设计。
本文使用激光扫描仪对室内场景建模并规划避障路径,采用四旋翼六自由度MPC控制策略,完成对避障航迹的准确跟踪。与其他文献不同,本文采用完整的四旋翼动力学模型,不仅考虑执行机构的动态特性,并且控制输入为传统的操纵杆量,使得所设计的控制律可以与物理平台直接对接。综上,给出了工程可行性高的室内飞行探索方案。
1 室内二维航迹规划
1.1 二维环境建模
本文以室内实际飞行环境为背景,如图1所示。通过激光扫描仪获得的环境信息对该场景建模,结果如图2所示。图中黑色线条为真实场景内的障碍物,如纸盒和墙边界。场景建模的范围为:

图1 实验场景
(1)
式中:xc和yc分别为四旋翼飞行器的x、y轴坐标,单位为mm。
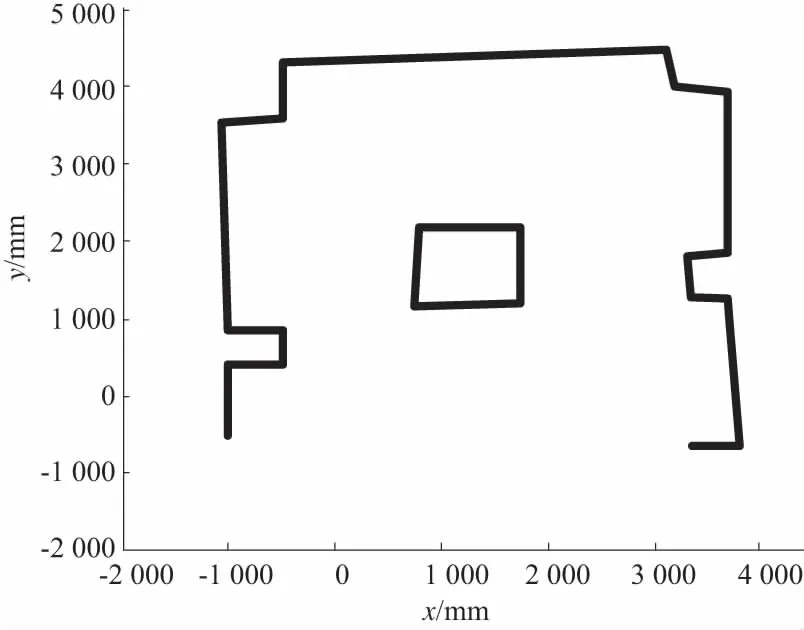
图2 场景模型
1.2 RRT算法
Cfree表示去除场景障碍物后的无障碍区域,用Tk表示建立的扩展树,为Tk扩展的步长,并令xinit和xgoal分别为初始点和目标点。则RRT算法流程如图3所示。
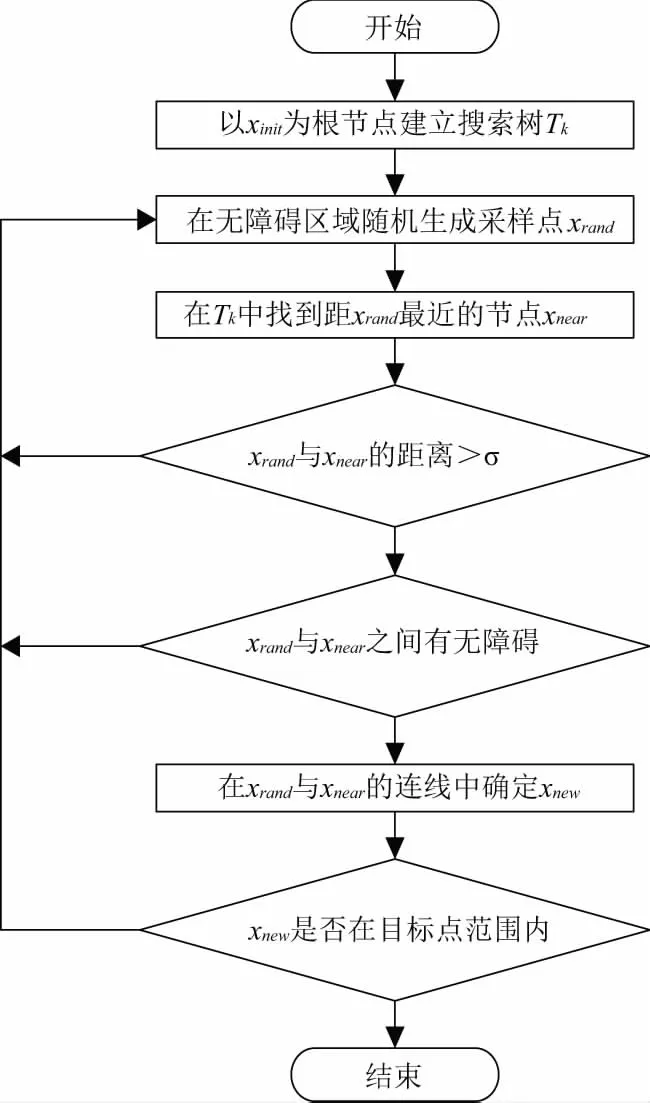
图3 RRT算法流程
1.3 规划航迹生成
由RRT算法原理可知其并不具备启发信息,而是通过随机生成采样点的方式来搜索空间,这会导致规划出的路径比较曲折,增加了航迹的长度和四旋翼飞行器的飞行难度。因此,需要对规划出的初始航迹进行平滑处理进生成参考飞行轨迹。
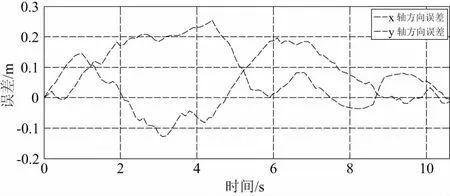
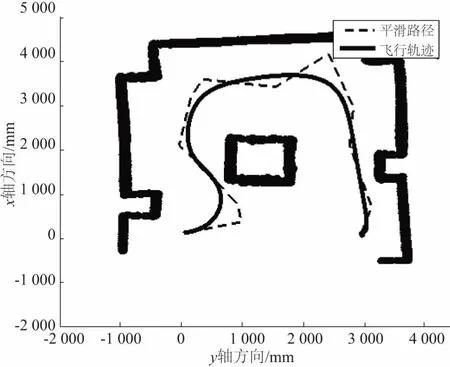
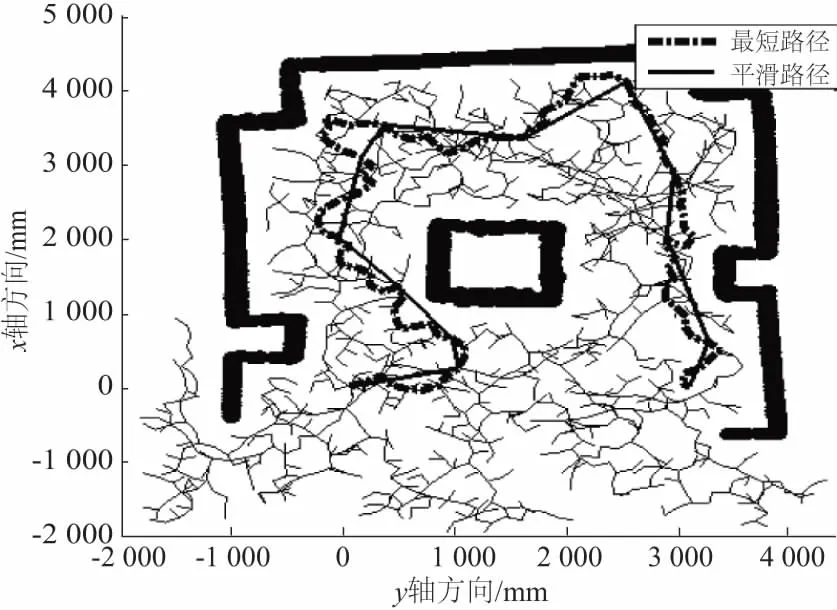
初始航迹平滑处理方法:针对规划出的航迹点,按10个1组的方式得到航迹段Pi(i=1,2,3…)。针对Pi和Pi+1,在2个航迹段中分别随机采样,连接随机采得的2个航迹点得到参考航迹段Ri[7]。并考虑3条限制条件:1)Ri与附近障碍物不发生碰撞;2)Ri与Ri-1斜率之差的绝对值 经过平滑处理得到每一段参考轨迹段Ri,考虑按长度平均的方式得到10个航迹点,其坐标作为航迹控制器的参考输入。 设计控制器对四旋翼位置和姿态的6个通道分别进行控制,控制结构如图4所示。外环是位置控制,给定输入为x、y、z三轴参考位置,输出是标准总距、期望滚转角和俯仰角的偏差量。内环完成姿态控制,输入是外环提供的期望滚转角和俯仰角偏差量以及期望偏航角,输出为滚转、俯仰、偏航通道标准杆量偏差量。 图4 MPC控制器结构示意图 首先将文献[8] 的四旋翼动力学模型进行线性化处理得到空间描述形式如式(2): (2) 控制量U、测量输出Y、状态量X依次为: U=[δcolδlonδlatδped]T Y=[xyzuvwφθψpqr]T X=[xyzuvwφθψpqrΩ1Ω2Ω3Ω4]T 其中,x、y、z为导航坐标系中机体重心位置,φ、θ、ψ为机体姿态角,p、q、r为角速度机体坐标分量。特别注意以上各变量含义是相对于平衡点的偏差量,并且各旋翼转速不可测量。由于四旋翼飞行器为线性时变系统,即反映特性的系数矩阵A、B会随着飞行状态的变化而改变,为了降低控制器设计复杂度,选择耦合程度最低的飞行器悬停点状态模型来设计。 由式(2)可得四旋翼六自由度通道输入输出传递函数。本节以俯仰通道为例,介绍其预测模型建立过程,其他通道类似。 俯仰通道输入输出传递函数: (3) 将式(3)离散化,定义k时刻俯仰通道控制输入量δlat(k)和输出量θ(k),再定义其z变换分别为u(z)和yo(z),则俯仰通道的离散特性可用如下脉冲传递函数来描述: (4) 在此基础上可得到俯仰通道离散化模型为: (5) 式中:xpitch=[yo(k)yo(k-1)yo(k-2)u(k-1)u(k-2)]T 对于上述离散化模型,参考经典预测模型建立方法[9]。定义状态增量与控制增量分别为: (6) 再定义增广状态向量: (7) 其中,r(k)为参考量。建立以xarg(k)为状态量,Δu(k)为控制量, 以跟踪误差为输出的滚转通道增广模型: (8) 由式(8)可建立如下形式的经典预测模型: Xarg=Exarg(k)+ΦΔU (9) 式中:E=[AA2A3…ANp]T, 使用拉盖尔基函数,以低维向量表征控制量序列,从而减少运算量[10]。拉盖尔基函数可用来表示各时刻最优控制增量,形式如式(10)所示: Δu(k+i)=L(k)η (10) 式中:η=[c1c2c3…cN]T。 将式(10)代入式(9)得到拉盖尔函数形式预测模型: (11) 预测控制器的增益通过最小化目标函数得到,本文使用成熟的二次型表达式[11]: (12) 把增广状态向量和用拉盖尔离散表达的最优控制增量式代入目标函数可得: (13) 式中:QL=CTQC,RL为对角矩阵,其阶数为所使用拉盖尔基函数维度N,对角线元素仍为权重值rw。为了将目标函数写成待求参数η的表达形式,代入式(11)的预测模型得: (14) 由于采用悬停点线性化设计,外环输出的期望姿态角偏差量需有0.2 rad的幅值约束,因此外环控制未来第k时刻控制量的幅值应该满足: umin≤Mkη+u(k-1)≤umax (15) 由式(15)可以写出如下线性不等式,M为约束边界。 (16) M的列数n表示要考虑未来第1到第n个时刻的约束条件。式(16)和(14)的求解为标准二次型优化问题。使用简单易行的希尔德雷思算法解决该问题[12],得到最优解: η=-H-1(G+MT*) (17) Δu(k)=L(0)Tη (18) 最优控制偏差量为u(k)=u(k-1)+Δu(k),该偏差加上配平值最终可得到最优输出量。 下面验证本文提出的室内环境飞行探索方案可行性。仿真结果的x、y轴位置跟踪误差如图5所示,实线是x轴方向跟踪误差,虚线是y轴方向跟踪误差。误差收敛至0.25 m范围内,有较好跟踪精度。最终轨迹跟踪效果如图6所示。第二节给出的参考航迹点坐标作为航迹控制器的参考输入,注意仿真中z轴参考位置设置为-1m。图7为航迹规划结果,RRT算法以增加节点的方式扩展随机树,完成该过程后,从目标位置点依次找父节点,直至找到根节点为止。这样规划出一条从初始位置到达目标点的无障碍最短路径,如图7虚线所示。经过平滑处理的参考航迹段如图7实线所示,可见曲折度明显减小而且航迹长度也被有效缩短 。 图5 轨迹跟踪误差 图6 轨迹跟踪效果 图7 航迹规划结果 基于激光扫描仪传感器建立的真实室内场景,由RRT算法规划出的路径并通过平滑处理得到曲折度较低的飞行轨迹。再基于单通道输入输出传递函数模型建立预测模型,进而设计级联形式的MPC控制器方案。最后以MATLAB仿真的形式验证了飞行控制效果,结果表明所设计的控制器有较好的控制性能,该飞行探索方案具有一定工程可行性。2 航迹、航姿控制器设计
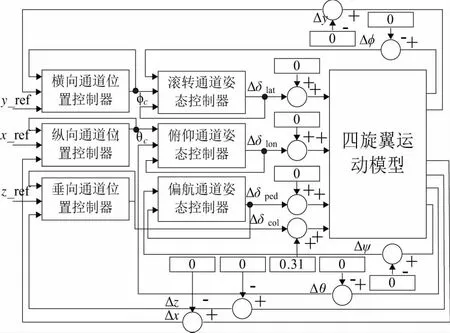
2.1 预测模型建立
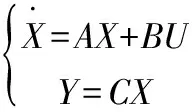

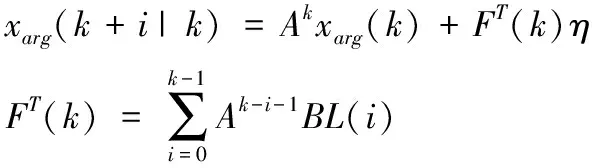
2.2 控制量推导
3 仿真结果
4 结语

