典型山地地形竖向风速分布特征

楼文娟, 梁洪超, 李正昊, 章李刚, 卞 荣

(1. 浙江大学 结构工程研究所, 浙江 杭州 310058；2. 国网浙江省电力公司经济技术研究院, 浙江 杭州 310000)

0 引 言

竖向风速对敞开的水平向结构和输电线路风偏十分不利，然而在目前的工程设计中，除大跨径桥梁颤振稳定性分析中考虑一定的风攻角外，一般的土木工程结构均忽略了上升气流的不利影响。在国外，对山地地形风场的研究自20世纪80年代便已经开始。Jackson 与 Hunt[1]首先对二维平滑低矮山地的风速分布进行了理论分析。由于其研究模型坡度平缓，山体风场中竖向风速分量较小，该部分竖向风速仅仅作为水平向风速的扰动进行了考虑。Jackson与Hunt这一研究基本确立了以风速加速比为主要参数的山地风场的研究方法。Taylor等[2]对上述理论计算公式进行修正，使当时的理论在缓坡条件下计算不同高度的风速加速比时更简便。Weng等[3]在计算过程中引入了粗糙度影响，使理论计算更加成熟。截止90年代，国外已经积累了相当的山地实测。Taylor等[4]对其进行整理，并与理论计算进行对比，认为加速比的理论计算结果在近地面处与实测结果差距较大。因此山地风场风速分布仍需要进一步的研究。在数值模拟与试验方面，Bitsuamlak等[5]整理并对比了二维陡坡、缓坡的数值模拟与风洞试验，认为数值模拟结果在迎风坡与试验能够较好匹配。Cao Shuyang 等[6-7]与Yassin等[8]采用二维CFD研究了山体粗糙度，山体坡度与来流湍流对山地风场加速效应的影响，其中Yassin等对比了二维CFD模拟与实验结果，认为其吻合程度较好，用CFD方法进行山地风场研究具有可行性。Takeshi等[9]利用自主研发的三维湍流风速测试装置对典型陡坡山体进行了实验研究，其研究在山体迎风坡观测到了相当于来流相同高度28.5%水平风速大小的竖向风速。然而其对竖向风速并未进行进一步详细研究。在国内，李正良等[10-13]对余弦形状山体分别进行了二维、三维数值模拟和试验研究。研究考察了山体高度、山体坡度与来流地貌等因素对山地风场加速比的影响，并对地形修正系数沿山坡分布情况进行了拟合。此外姚旦[14-15]对余弦形单山、双山也进行了细致的试验与数值模拟研究，研究提供了较为详细的数值模拟方法，且模拟结果与试验结果吻合程度较好。

上述研究工作加深了对山地地形风场分布的认识，提供了较为成熟的风洞试验与数值模拟方法。然而，上述研究存在以下两点不足：其一，目前的大部分研究着重于顺风向风速分布，风洞试验中亦只测定顺风向风速，而对于竖向风速分布及其随着山高、坡度等形状参数变化的研究处于空白状态。实际工程中竖向风速的存在会影响山地地形中工程结构的使用与安全。例如在山区输电线路中，上升气流会将导线上托，减小导线张力，从而导线产生更大的风偏角而发生闪络事故。故应当对竖向风速分布及其随山体形状参数变化进行研究；其二，目前研究的山体大多为无山脉长度的三维轴对称山体(“馒头山”)或山脉长度无穷大的二维山体，并未研究山脉长度介于两者之间的情况。虽然国外研究了具有长短轴的椭圆山体模型[16]，但该研究实质仍是无山脉长度的山包。由于实际山体往往具有一定的山脉长度，而且山脉长度可能对山地风场的分布情况产生显著影响[17-18]，故应当对不同山脉长度下的山地风场进行研究。

在此研究背景下，本文参考以往研究，对具有一定山脉长度的陡坡山地模型进行了风洞试验，在该风场中测试得到了竖向风速分布。而后对照试验结果利用求解雷诺时均N-S方程(Reynolds-Averaged Navier-Stokes，RANS)模拟得到不同形状参数下山地地形平均风场信息，用以研究典型山地地形竖向风速的大小，分布及其随山高、坡度、山脉长度的变化，为实际山地中的工程建设提供参考。

1 风洞试验

1.1 试验概况

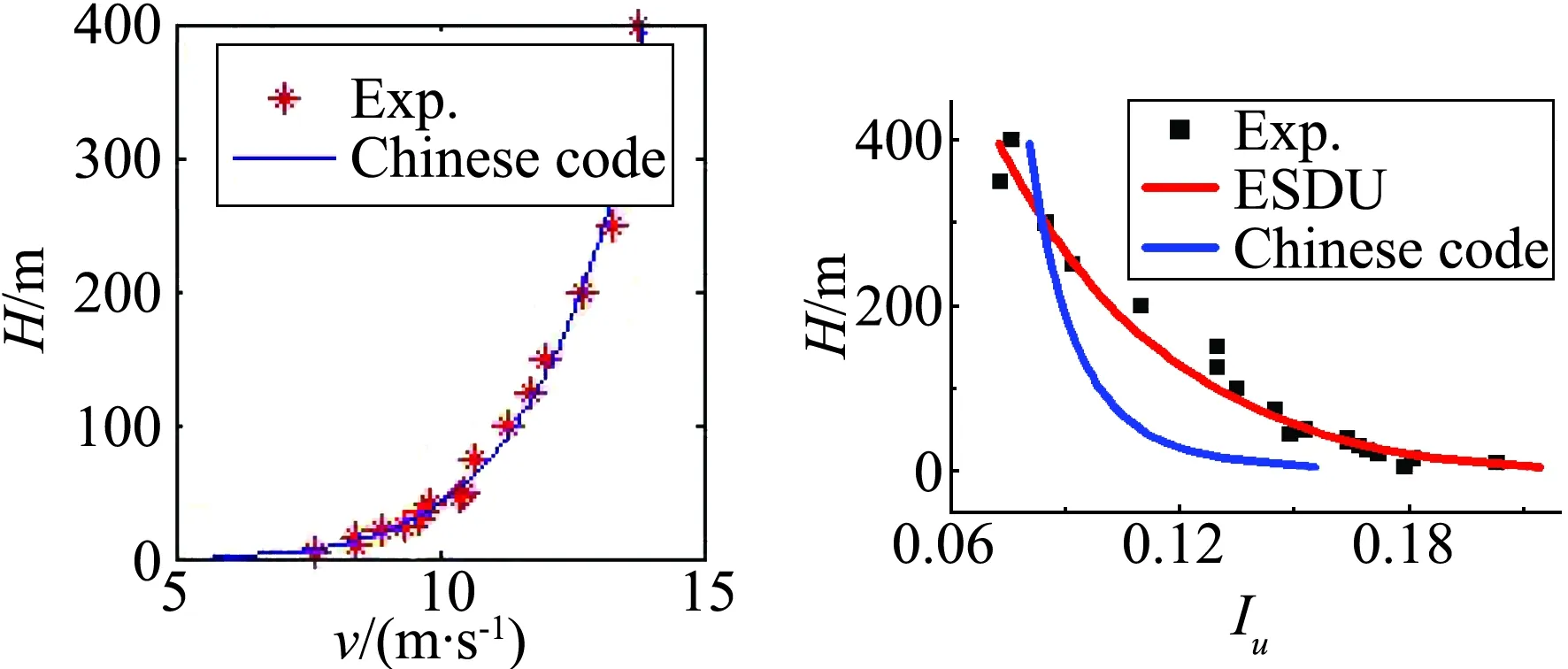
本次试验在浙江大学ZD-1风洞中进行。本文研究的山体形状为目前研究最广泛，且与实际山体较为接近的余弦形。其横截面定义如式(1)所示。其中H为山体高度，D为山体底面圆直径。

试验地形山底直径300 m，山高100 m，具有300 m的山脉长度。模型表面覆盖绿色纤维，用以增加山体表面粗糙度，以减小雷诺数效应对试验近地面结果的影响。模型图片如图1所示。试验几何缩尺比为1∶500，来流为相同比例B类地貌来流。来流平均风剖面如图2(a)所示，试验剖面与规范平均风剖面能够较好吻合，试验原型10 m高度处风速为8.10 m/s。试验测点三维风速测定采用澳大利亚TFI(Turbulence Flow Instruments)公司生产的眼镜蛇湍流风速测量仪(Series 100 Cobra Probe)。眼镜蛇三维脉动风速探头是4孔压力探头，可用于测量三维风速和静态压力。试验对来流风速三维脉动情况进行了测试，测得三维湍流度如图2(b～d)所示。测试所得顺风向湍流度略大于B类规范规定的湍流度，与ESDU规定的三维湍流度吻合较好。试验测点布置和风向角定义如图3所示，试验工况来流为90°风向角。试验测点布置在山脊与迎风坡处，测点分为实心测点与空心测点，实心测点测定了离地10～400 m高度的三维风速，空心测点只测定离地10 m高度处的三维风速。

图1 试验模型照片Fig.1 Photo of experiment model

(a) 来流平均风剖面 (b) 来流顺风向湍流

(c) 来流横风向湍流 (d) 来流垂直风向湍流

图2试验来流条件
Fig.2Inletconditionofexperiment

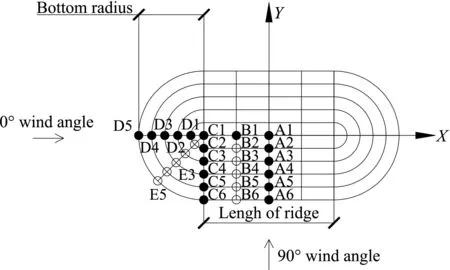
图3 风向角定义和测点布置Fig.3 Definition of wind angle and layout of measurement points

1.2 试验结果

图4展示了迎风坡离地10 m高度处竖向风速分布情况，其中正值竖向风速为上升气流，负值竖向风速为下降气流。由试验结果可知，上升气流在迎风坡上普遍存在，其中上升气流风速出现临近山脊的2/3山体高度以上区域。

试验各测点中，A1位置处为山脊位置，该处竖向风速在2.5 m/s左右，为来流风速(8.10 m/s)的31%。A2位置处为迎风坡,竖向风速达约5.5 m/s，占来流水平风速68%，由此说明了山地地形中竖向风速占到来流较大比重，应当在工程实践中予以重视。

2 CFD数值模拟与验证

2.1 建模概况

本文采用CFD模拟进行大量工况的研究。为了计算结果更准确，收敛速度更快，模拟时统一流场尺寸设定，流场横向尺寸为7(L+D)，纵向尺寸为11(L+D)+D，其中L为山脉长度，D为山体底面直径，流场高度为6倍的山体高度。流域的阻塞比在3%以下，如此较好的保证了流场的充分发展。网格划分时，山体表面网格尺寸为5 m，底面网格尺寸扩展率为1.05，最大网格尺寸为30 m。竖向首层网格尺寸为1 m，竖向扩展率为1.1，竖向最大网格尺寸为20 m。网格划分采用cooper方法。入口采用速度入口，出口采用自由出口，地面与山体采用壁面，侧面与顶面采用对称面。地面粗糙高度为0.5 m，山体表面粗糙高度为1 m。

模拟采用入口条件为规范B类地貌来流，湍流模型选取Realizablek-ε模型，采用非平衡壁面函数(Non-Equilibrium Wall Function)。风剖面与湍动能剖面如式(2)～式(5)定义[19]:

k(z)=0.5[U(z)×I(z)]2(3)

Lu=0.2(y/30)0.5(5)

其中，Z0和U0分别表示标准参考高度和标准参考风速，本文取10 m和10 m/s，剖面指数α对B类地貌取为0.15。I(z)表示z高度下的湍流度，按照日本规范[20]的定义计算。Cμ取值为0.09,K取值为0.42，Lu为湍流积分尺度，同样以日本规范定义。

图5为CFD入口处与距入口1000 m位置风剖面情况的对比，有对比可知入口平均风剖面具有良好的自保持性。在此条件下入口湍流度剖面的自保持性不佳，但由于文中仅针对平均风场进行研究，应优先考虑平均风剖面的自保持性，且湍流剖面对平均风的计算结果影响较小，因此可暂时降低对入口湍流剖面的要求[17]。

图5 CFD入口条件及其自保持性Fig.5 CFD inlet condition and its self-maintenance

2.2 CFD方法的验证

本文进行了风洞试验工况的数值模拟，并对比了两者加速比与竖向风速结果，加速比按式(6)定义:

其中，Ux为水平风速，U0为相同离地高度来流水平风速。

CFD结果对比情况如图6所示，试验与CFD的水平风速加速比在山顶与山脚处吻合较好，在山腰流场复杂区域，两者结果有些差异，但总体趋势吻合。此外，试验与数值模拟结果中竖向风速分量在各个区域吻合程度普遍较好。

为了进一步验证本文CFD方法，对参考文献[9]研究的40 m高，底部直径200 m的三维轴对称山体进行建模计算。如图7所示，CFD加速比结果与Takeshi的研究结果同样具有很好的吻合程度。因此通过本文的CFD方法整理总结竖向风速在典型山地中的分布具有可行性。

(a) 水平风速加速比

(b) 竖向风速

(a) 山脚位置

(b) 迎风坡位置

(c) 山顶位置

3 CFD研究典型地形竖向风速分布

3.1 轴对称山体

本文对无山脉长度的“馒头山”进行详细研究。研究不同山体高度，坡度下竖向风速的分布情况。工况设置如表1所示。

表1 轴对称山体模拟工况设置Table 1 Case of numerical simulation with axisymmetric hill

3.1.1 山体高度对竖向风速分布的影响

图8(a)所示为竖向风速比Rz沿山体迎风坡中轴线的分布。其中x含义与图3相同，在不具有山脉长度的情况下，-2x/D为0和1时分别位于山顶与迎风山脚。在本文中，竖向风速比Rz按式(7)定义:

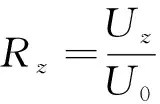
其中,Uz、U0分别为竖向风速和相同离地高度来流水平风速。

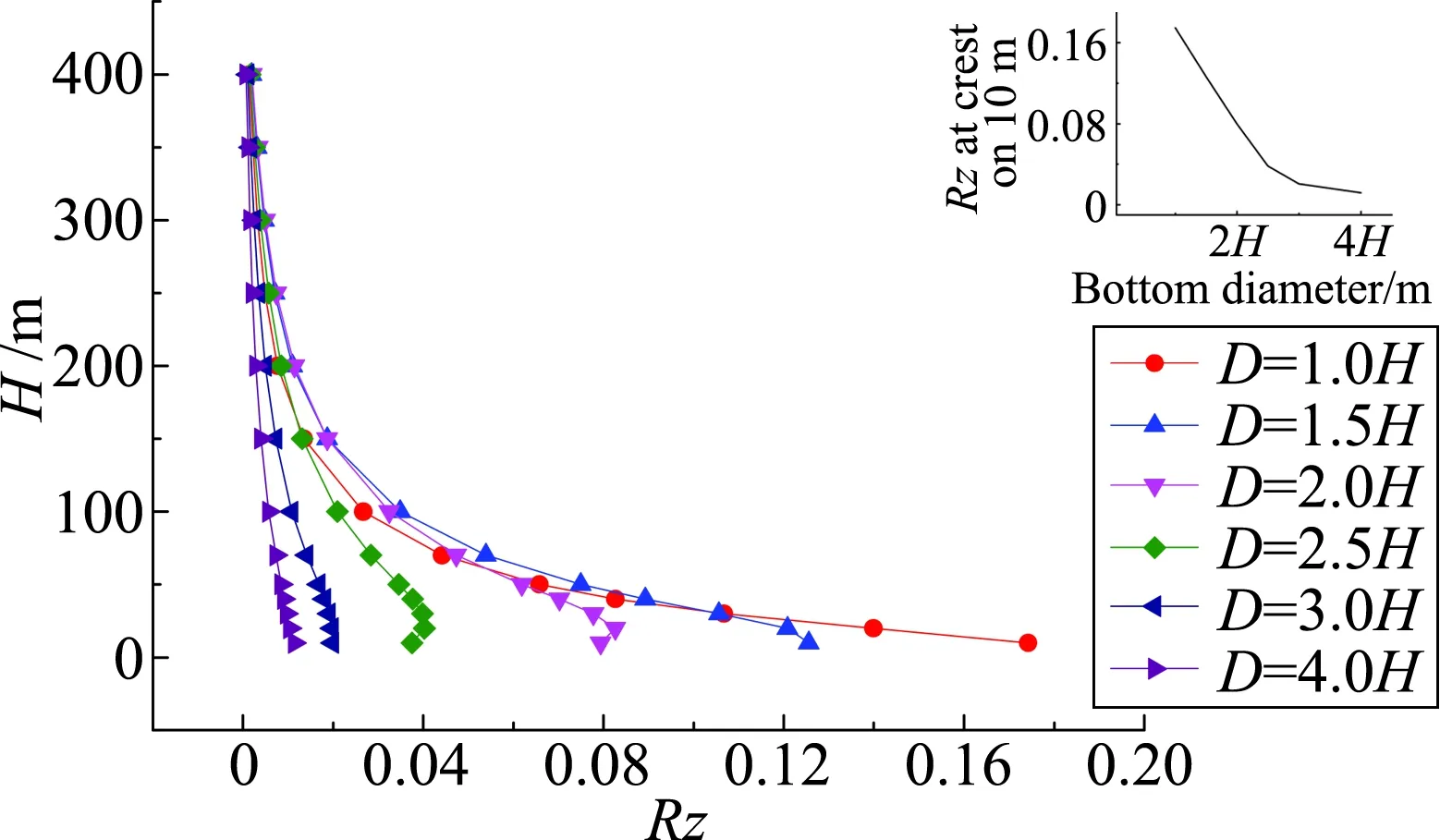
如图8(a)所示，不同山体高度下，迎风坡最大竖向风速比均出现在山坡2/3山高以上的位置，且出现位置随山体高度增加略为上移。最大竖向风速比数值随山体高度增加而增加，从山高50 m至山高400 m，迎风坡最大竖向风速比增加为188.12%。-2x/D小于0.8的区域，即迎风坡1/3山高以上区域，离地10 m高度的竖向风速均占来流10%以上。因此在迎风坡1/3山高以上区域应适当考虑竖向风速。

图8(b)所示为不同山体高度，山顶处竖向风速比随离地高度的变化情况。如图所示离地10 m处的竖向风速比随山体高度先增加后减小，山体高度为100 m时山顶离地10 m高竖向风速比存在最大值。从山顶竖向风速比剖面来看，山体高度在100 m以下时，最大竖向风速比出现在离地10 m高度处，竖向风速比随离地高度增加而减小。当山体高度大于200 m时，竖向风速比随离地高度先增加后减小，最大竖向风速比出现的离地高度也随山体高度增加而递增，在山高400 m时，最大竖向风速比出现在离地75 m左右。

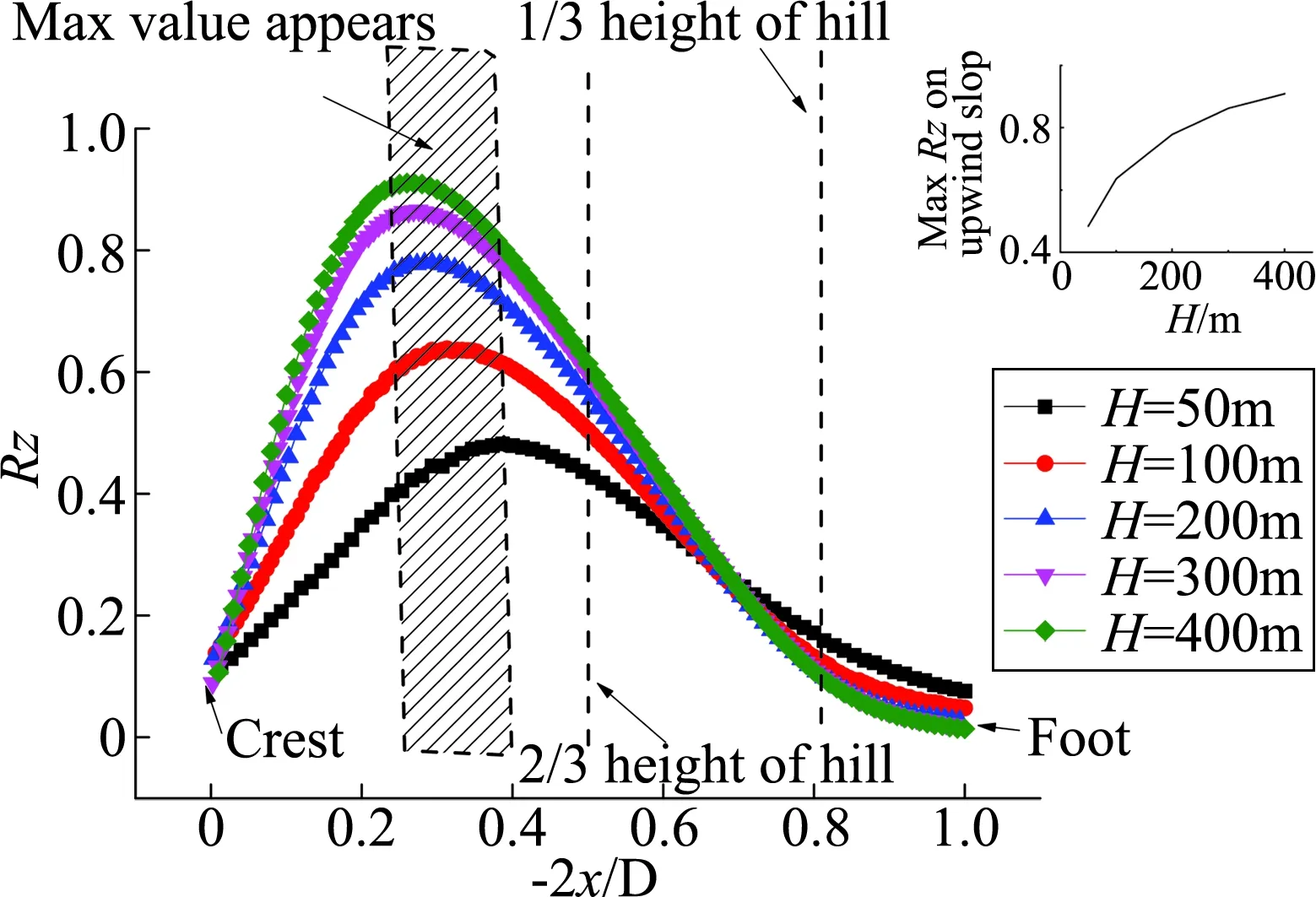
(a) 迎风坡竖向风速比分布

(b) 山顶竖向风速比剖面

3.1.2 山体坡度对竖向风速分布的影响

如图9(a)所示在山体高度一定时，不同山体底部直径下竖向风速比沿迎风坡中轴线的分布情况。如图所示，在山体高度一定时，迎风坡最大竖向风速比随着底部直径增大而减小，底部直径8H时最大竖向风速比为底部直径2H时的55.64%。最大竖向风速比出现的位置同样保持在2/3山高以上的迎风坡处，且随着底部直径增大而逐渐下移。在山体底部直径变化时，-2x/D大于0.8的区域，即迎风坡1/3山高以上区域，离地10 m高度的竖向风速比同样均占来流10%以上。

如图9(b)所示，相同山体高度时,山顶最大竖向风速比随着山体底部直径增加而递减。值得注意的是在底部直径小于5H时，山顶的竖向风速均占来流风速5%以下，此时山顶位置可不考虑竖向风速。

3.2 不同山脉长度下的竖向风速分布

本节主要研究山脉长度对竖向风速分布的影响。表2展示了含山脉山体的模拟工况。该处H与D分别固定为100 m 和300 m 。其中风向角定义如图3所示。

(a) 迎风坡竖向风速比分布

(b) 山顶竖向风速比剖面

Wind angleRidge length L90°0H, 0.5H, 1.0H, 2.0H, 3.0H, 4.0H, 5.0H, 8.0H0°0H, 1.0H, 3.0H, 5.0H, 8.0H

3.2.1 来流风向垂直山脉(90°风向角)

如图10所示，迎风坡坡最大竖向风速比与山脊中部竖向风速比在离地10 m 处均随着山脉长度递增，且递增趋势逐渐放缓。这是由于在该风向角下，来流正对山脉，山体中部绕流随着山脉长度增加逐渐接近二维情况，越山效应更为显著。山坡最大竖向风速比与山脊中部竖向风速比从“馒头山”至山脉长度达8H情况，增幅分别达15%和87%。当山脉长度达到8H时，山脊中部竖向风速比可达0.29。

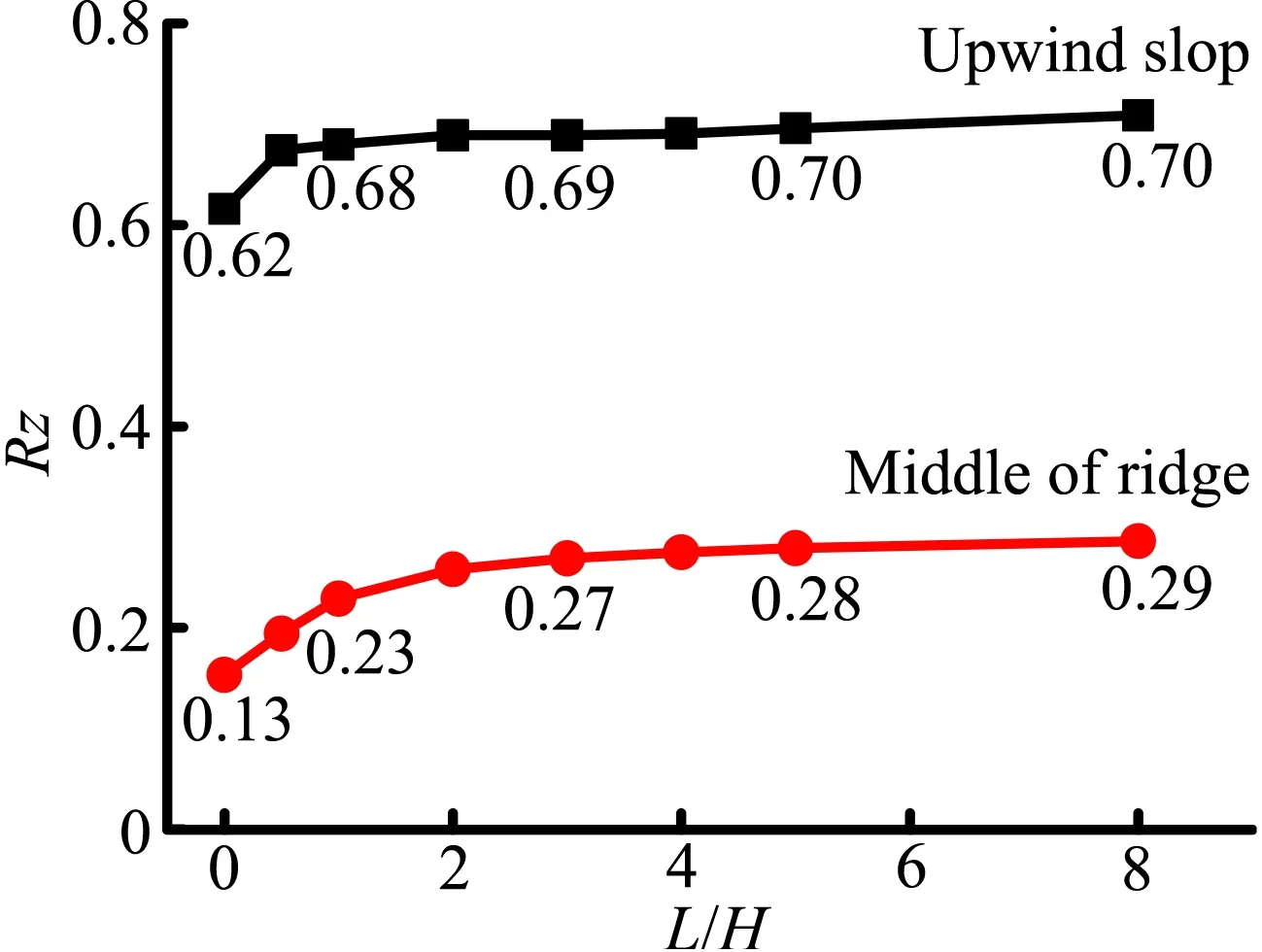
图10 90°风向角10 m高度竖向风速比Fig.10 Vertical wind velocity ratio at the height of 10 m under 90° wind angle

如图11所示为离地10 m高度竖向风速比沿山脊的分布情况。其中x含义如图3所示，L表示山脉长度。x/L为-0.5与0.5时，分别为山脊左、右侧端部。如图所示竖向风速比在山脊中间较大，在左右侧较小。其原因是山脊中部越山效应更加明显。相同山脉长度下，竖向风速比沿山脊的变化主要发生在左右端部1/10L范围内，在山脊中间区域变化相对平缓。随着山脉长度增加，山脊端部的竖向风速比变化不明显，而山脊中部竖向风速比明显增加。

图11 90°风向角10 m高度竖向风速比沿山脊变化Fig.11 Vertical wind velocity ratio changes along the ridge at the height of 10 m under 90° wind angle

3.2.2 来流风向顺山脉(0°风向角)

图12所示为来流顺山脉情况下，迎风坡与山脉最大竖向风速比随山脉长度变化情况。如图所示，迎风坡最大竖向风速比随山脉长度增加显著减少，并在山脉长度达到5H后保持不变。山脉长度为5H时迎风坡最大竖向风速比仅为“馒头山”情况的58%。山顶最大竖向风速比随着山脉长度的变化几乎不发生改变。

图12 0°风向角10 m高度竖向风速比Fig.12 Vertical wind velocity ratio at the height of 10 m under 0° wind angle

在该风向角下，离地10 m高度处的竖向风速比沿山脊分布如图13所示，x/L为-0.5与0.5时，分别代表迎风坡山顶与背风坡山顶。来流到达山体，在迎风坡山顶为上升气流，在山脊中间区域几乎为0，当接近背风坡时，转变为了下降气流。当山脉长度大于3H，山脊上竖向风速比变化主要集中在靠近迎风坡和背风坡的1/10L区域内。

图13 0°风向角10 m高度竖向风速比沿山脊变化 Fig.13 Vertical wind velocity ratio changes along the ridge at the height of 10 m under 0° wind angle

4 结 论

本文首次尝试研究了山地地形中的竖向风速分布随山体高度、坡度和山脉长度的变化。研究发现竖向风速在不同山体高度、坡度和山脉长度的山地地形中普遍存在。由试验结果可知，在陡坡山地地形中竖向风速可达到来流风速60%以上，应当在工程实践中予以重视。本文填补了工程中无法参照已有研究考虑竖向风速的空白。

本文研究中考虑了山脉长度对山地竖向风速分布影响，发现山脉长度显著影响山地地形中的竖向风速分布，且竖向风速沿山脊分布主要在接近两侧山顶的1/10山脉长度范围内发生变化。在对山地地形风场的研究中考虑山脉长度的影响是必要的。

本文研究仅展示了竖向风速在山地地形中的分布情况，而对其分布的拟合及如何有效在工程设计中考虑竖向风速仍有进一步研究的需要。