土质地层中隧道上覆荷载计算研究

宋 艺



土质地层中隧道上覆荷载计算研究

宋 艺

（中铁第一勘察设计院集团有限公司，西安 710043）

在隧道结构计算分析时，如何计算确定作用在隧道结构上的上覆荷载的大小及分布是设计的关键。对于土质地层中的隧道，埋深较浅时上覆荷载计算时常采用全部覆土重量，而当土层较厚，隧道埋深较大时通常会采用太沙基公式、普氏压力拱理论公式及隧道设计规范公式等，这些公式在选用时尚存在一些问题，通过对比隧道在土质地层中几种公式计算的上覆荷载规律，分析各计算公式存在的问题，加以改进推导出了隧道在土质地层中竖向荷载的建议计算公式，并通过全国各地区实测数据加以验证。研究结果可为类似条件下工程的设计提供借鉴和参考。

土质地层；隧道埋深；上覆荷载；计算公式

目前我国城市轨道交通工程正处于快速发展时期，隧道在结构设计时如何确定作用在隧道结构上的上覆荷载大小及分布是设计的关键[1-3]。

《地铁设计规范》规定“地层压力应根据结构所处工程地质及水文地质条件、埋置深度、结构形式及其工作条件、施工方法及相邻隧道间距等因素，结合已有经验、测试和研究资料，按有关公式计算或依工程类比确定”。条文说明中解释：地层压力是地下结构承受的主要荷载[4]。一般情况，石质隧道可根据围岩分级，依工程类比确定围岩压力；填土隧道及浅埋暗挖隧道一般按计算截面以上全部土柱重量考虑；深埋隧道按太沙基公式、普氏公式或其他经验公式计算[5]。在实际工程中，处于软土或砂层中的隧道顶部所受竖向压力经常取全部土层重量，这样在埋深增大时势必导致荷载急速增大，计算出的结构尺寸和配筋与实际差异较大。当采用《铁路隧道设计规范》中给出的深浅埋隧道计算公式计算砂层中的隧道结构时，需对隧道穿越地层进行围岩分级并考虑内摩擦角和计算摩擦角，在这些值的选取时存在一定的人为因素，而且同一隧道随埋深的增大，在达到一定深度后垂直荷载会产生突变，从而导致计算结果不统一或与常规认识和实测结果不一致[6]。因此在土质地层中的隧道计算上覆荷载时何时采用全土柱计算公式、何时不能采用、何时为深埋隧道、各埋深下上覆荷载大小及全土柱法和压力拱法的覆土分界厚度等一直是比较模糊的问题，不同的设计单位采用不同的设计方法并偏于保守的考虑使得同一埋深下的隧道配筋差别很大，很难实现安全、经济、合理的统一[7]。

本文针对上述问题，分析了在土质地层中隧道结构计算的几种常用上覆荷载计算方法，比较了其计算结果，并结合各公式的优缺点及各地实测数据分析，推导了一种计算上覆荷载的计算公式，并与国内类似地层中的隧道上覆荷载实测值进行了比较，所得结果可为隧道结构设计提供借鉴和参考。

1 常用上覆荷载计算方法及比较分析

1.1 全土柱法

该方法认为作用在隧道上部的垂直荷载即为隧道宽度范围内的覆土重量，忽略土体间的竖向摩擦力，计算公式如下：

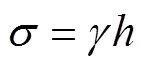
式中土体容重根据水位的不同分别采用天然容重和浮容重。

1.2 太沙基理论

太沙基理论是以松散介质平衡理论为基础的计算方法，从应力传递概念出发，考虑了隧道尺寸、埋深、土层黏聚力和内摩擦角对土体稳定的影响，认为隧道开挖后，顶部土体在重力作用下向下移动，在隧道两侧至地面出现了两个剪切面，作用在两个侧面上的剪切力，采用微积分的方法，通过积分得到结果[8]。

根据太沙基理论推导出的隧道顶部垂直压力计算公式如下：

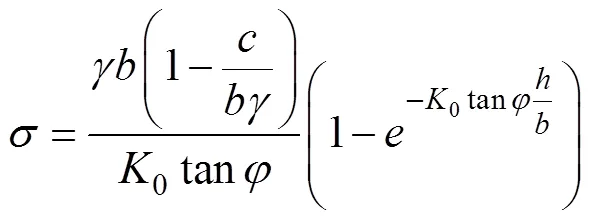
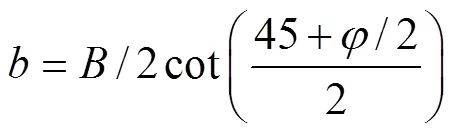
在砂层中时计算采用水土分算，即采用浮重度计算土压力，然后再叠加水压力。

1.3 普氏理论

普氏理论认为，对于那些整体性较差的围岩，可将其视为具有一定黏聚力的松散体，当洞室开挖以后，首先会引起洞顶岩石塌落。这种洞顶岩石塌落是有限的，当塌落到一定程度以后，岩体就会进入新的平衡状态，形成自然平衡拱[9]。其计算公式如下：

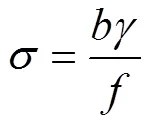
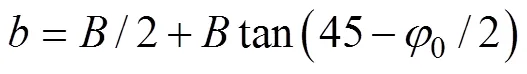
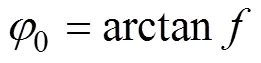
在砂层中计算时采用水土分算，即采用浮重度计算土压力，然后再叠加水压力。

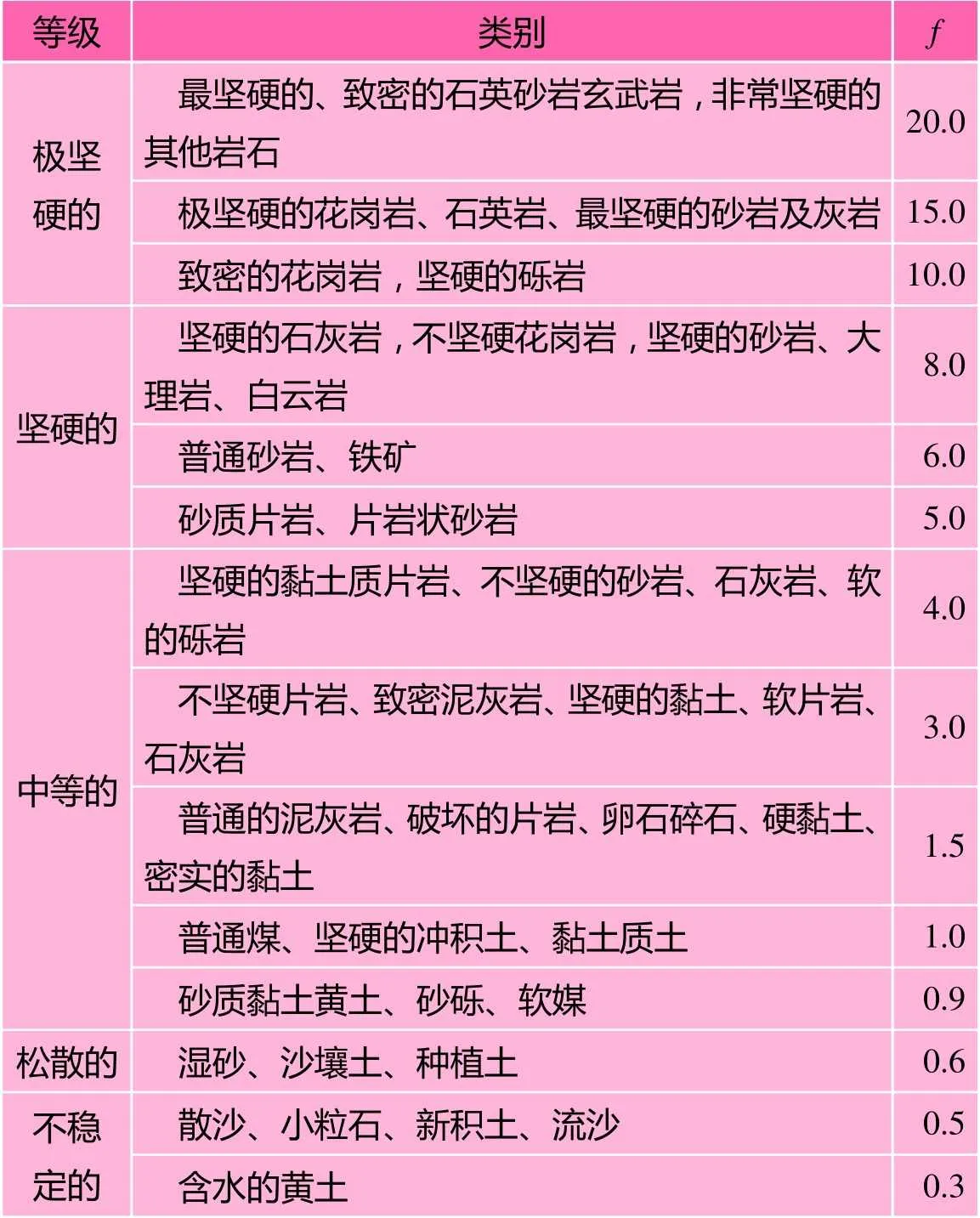
表1 普氏系数取值

1.4 规范公式

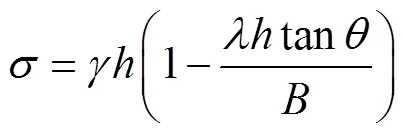
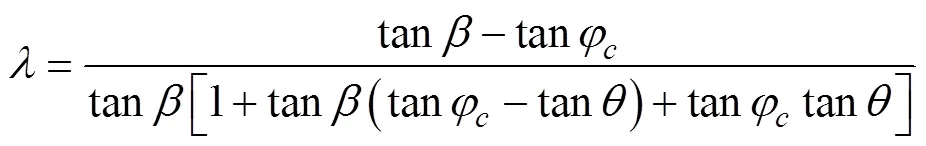
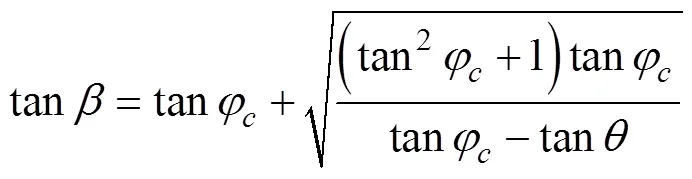
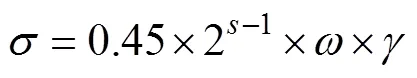
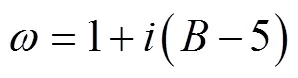
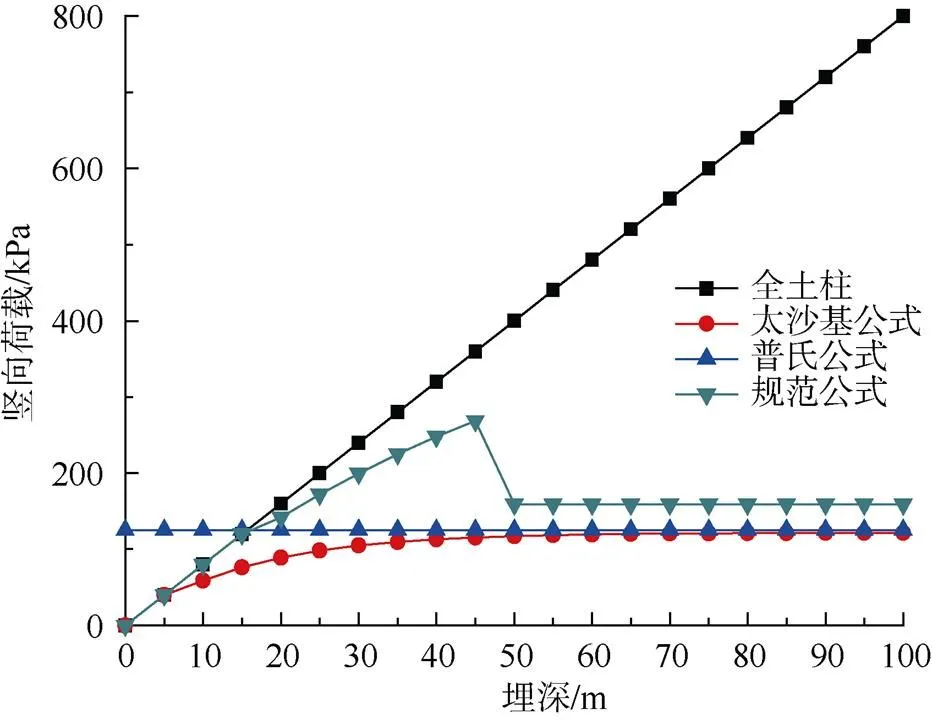
图1 各公式上覆荷载计算值曲线图

从图1可以看出：

1）当上覆土厚度在1倍隧道宽度以下（即≤）时，采用全土柱法，太沙基公式、规范公式的结果是基本一致的，普氏公式则偏大很多。

2）上覆土厚度大约在16 m左右（即大约为2）时，采用全土柱法，普氏公式和规范公式的计算值是一致的，太沙基公式计算结果则偏小。

3）上覆土厚度大于16 m以后，全土柱法和规范公式计算的荷载值不断增大，全土柱法上升得更快，而太沙基公式和普氏公式计算的值则逐渐趋于一致且小于规范公式。

4）全土柱公式在埋深逐渐增大时，上覆荷载成直线上升且增长较快，这与实测结果并不相一致。

5）规范公式在上覆土厚度大约为45 m（即大约为5）时，荷载达到最大值，之后上覆荷载值出现较大幅的突然降低，并达到平稳，这与常规的认识不一致。

6）普氏公式中上覆荷载值的计算与覆土厚度无关，普氏系数的选取较人为化，且其50年代传入中国时，前苏联有关文献就已经指出，对于松软地层普氏公式计算结果比实测压力偏低，因此在土质地层中若采用普氏公式或太沙基公式计算，则可能导致结果偏小，设计偏不安全[11]。

2 竖向荷载表达式

针对上述规律及各公式存在的问题，总结各公式优缺点后加以改进，改进思路如下：

1）隧道埋深在1倍隧道宽度和2倍隧道宽度以下时，各有3种计算公式结果一致，因此推荐隧道埋深在2倍隧道宽度以下时定为超浅埋隧道，计算时仍采用全土柱法。

2）隧道埋深大于2倍隧道宽度后，计算公式沿用规范公式中浅埋隧道计算公式的思路，并建议将公式中的计算摩擦角等人为经验数值，换为隧道宽度、内摩擦角等一些较为明确或实验可准确得到的数值。

3）深浅埋分界时，不应出现压力突变，而认为当两侧土体挟持作用随埋深增加到使上覆土压力达到定值或最大值时，此时埋深即为深浅埋的分界，土压力平顺过度，不出现突变[12]。

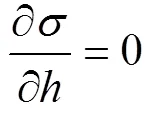
计算所得公式如下：

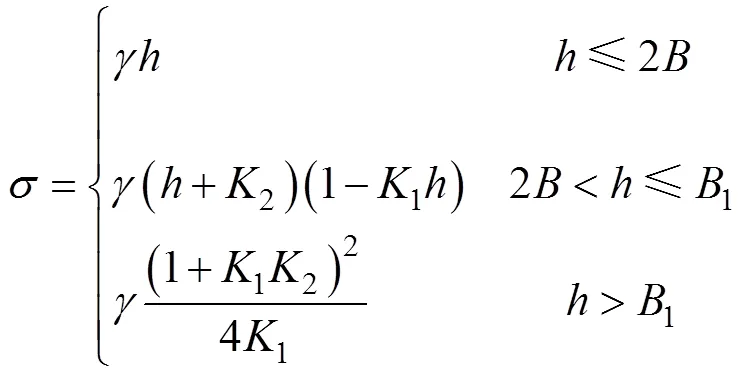
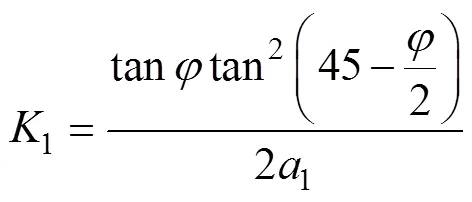
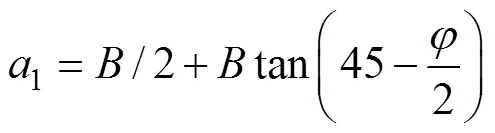
由图2可以看出：1）各埋深下上覆竖向荷载均平顺过度，未出现突变和跳跃；2）在埋深大于一定深度时竖向荷载趋于一个定值不再增长，这与前述计算方法所得结果及实际认识是一致的；3）计算结果较之普氏公式和太沙基公式结果略偏大。

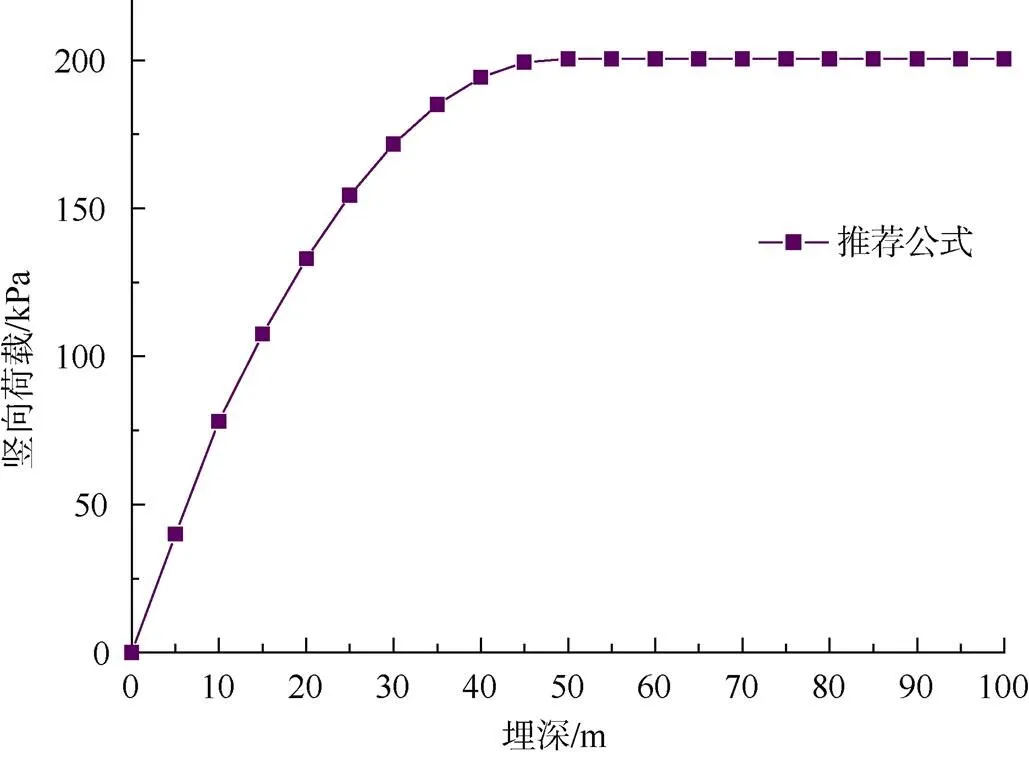
图2 推荐公式上覆荷载计算值曲线

3 实测数据分析与比较

针对上述几种上覆荷载计算公式，下面结合实测土压力来分析几种计算方法的计算结果与实测土压力值的关系，结果见表2。

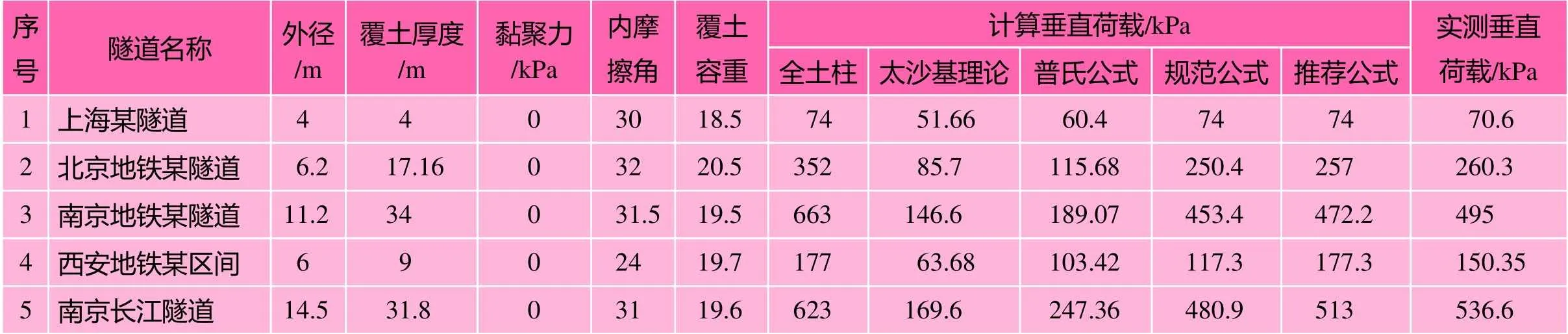
表2 各隧道实测土压力与计算土压力比较[13-15]

由上表可以看出公式计算结果与实测垂直荷载较为接近。隧道埋深在2倍洞径以内时太沙基理论及普氏公式计算结果较实际略偏小，这与之前的认识一致。

4 结论

通过上述的分析可得以下结论。

1）隧道上覆荷载常用计算方法为全土柱法、太沙基理论、普氏公式及规范公式，通过对比4种公式的计算结果，发现隧道埋深在2倍隧道宽度以下时，各计算公式计算结果差异不大，所得结果均与实际相近。

2）隧道埋深在2倍隧道宽度以上时全土柱法计算所得结果相较于其他公式偏大且增长较快，太沙基理论和普氏公式的计算结果则均偏小；当隧道埋深在大约5倍隧道宽度时规范公式计算结果存在突变，之后结果与太沙基理论和普氏公式所得结果趋势一致，均趋于一个定值。

3）总结分析4种上覆荷载计算公式（全土柱法、太沙基公式、普氏公式、规范公式）的优缺点，考虑用实验可得到的隧道宽度，内摩擦角等代替常用计算公式中的经验数值，推导了土质地层中隧道上覆荷载的建议计算公式，并与实测数据进行了比较，结果表明推荐公式计算结果更接近实测值，所得结果供隧道及地下工程设计计算时参考。

[1] 李雪, 周顺华, 王培鑫, 等. 盾构隧道实测土压力分布规律及影响因素研究[J]. 岩土力学, 2014, 35(S2): 453- 459. LI Xue, ZHOU Shunhua, WANG Pengxin, et al. Study of distri­bution law of earth pressure acting on shield tunnel lining based on in-situ data[J]. Rock and soil mechanics, 2014, 35(S2): 453-459.

[2] 周松, 韩磊, 叶冠林, 等. 浅覆土大断面盾构隧道横截面受力变形特性研究[J]. 土木工程学报, 2015, 48(S2): 284-287. ZHOU Song, HAN Lei, YE Guanlin, et al. Analysis on inner force and deformation characteristics of large shallow shield tunnel cross section[J]. China civil engineering journal, 2015, 48(S2): 284-287.

[3] 李鹏飞, 周烨, 伍冬. 隧道围岩压力计算方法及其适用范围[J]. 中国铁道科学, 2013, 34(6): 55-60. LI Pengfei, ZHOU Ye, WU Dong. Calculation methods for surrounding rock presser and application scopes[J]. China railway science, 2013, 34(6): 55-60.

[4] 地铁设计规范: GB 50157—2013[S]. 北京: 中国建筑工业出版社, 2014. Code for design of metro: GB 50157-2013[S]. Beijing: China Architecture & Building Press, 2014.

[5] 钟小春. 盾构隧道管片土压力的研究[D]. 南京: 河海大学, 2005. ZHONG Xiaochun. Research on earth pressure for shield tunnel lining[D]. Nanjing: Hohai University, 2005.

[6] 孙文昊. 土质地层中盾构隧道垂直荷载计算方法探讨[J].铁道工程学报, 2009, 26(10): 69-73. SUN Wenhao. Research on the calculation method for vertical earth pressure of shield tunnel in Soil layer[J]. Journal of railway engineering society, 2009, 26(10): 69- 73.

[7] 熊驷东. 盾构隧道管片结构优化设计研究[D]. 武汉: 武汉理工大学, 2014. XIONG Sidong. Research on optimization of the shield tunnel segments’ design in structure[D]. Wuhan: Wuhan University of Technology, 2014.

[8] 程小虎. 土质隧道深浅埋分界的理论解析[J]. 地下空间与工程学报, 2012(1): 37-42. CHENG Xiaohu. Theoretical solution for the dividing depth of deep tunnel and shallow tunnel in Earth[J]. Chinese journal of underground space, 2012(1): 37-42.

[9] 高攀科. 普氏卸荷拱理论在治理隧道塌方中的应[J]. 甘肃水利水电技术, 2011, 47(4): 50-51. GAO Panke. Application of platts unloading arch theory in tunnel collapse control[J]. Gansu water conservancy and hydropower technology, 2011, 47(4): 50-51.

[10] 铁路隧道设计规范: TB 10003—2016[S]. 北京: 中国铁道出版社, 2017. Code for design on tunnel of railway: TB 10003—2016[S]. Beijing: China Railway Publishing House, 2017.

[11] 林乐斌, 刘寒冰, 刘辉. 隧道围岩压力的应力分析方法[J]. 土木工程学报, 2007, 40(8): 85-89. LIN Lebin, LIU Hanbing, LIU Hui. Stress analysis method for pressure of sur rounding rocks on tunnels[J]. China civil engineering journal, 2007, 40(8): 85-89.

[12] 宋玉香, 贾晓云, 朱永全. 地铁隧道竖向土压力荷载的计算研究[J]. 岩土力学, 2007, 28(10): 2240-2244. SONG Yuxiang, JIA Xiaoyun, ZHU Yongquan. Study on vertical earth pressure calculation of metro tunnel[J]. Rock and soil mechanics, 2007, 28(10): 2240-2244.

[13] 王建军, 丁洲祥, 刘辉. 土质地层中盾构施工引起的土体应力变化规律[J]. 山西建筑, 2010, 36(12): 323-324. WANG Jianjun, DING Zhouxiang, LIU Hui. On the soil variation of construction of water-rich sand in the shield[J]. Shanxi architecture, 2010, 36(12): 323-324.

[14] 张旭东. 土压平衡盾构穿越土质地层施工技术探讨[J]. 岩土工程学报, 2009, 31(9): 1445-1449. ZHANG Xudong.Construction technology of earth pre­ssure balance shield in watery sandy stratum[J]. Chinese journal of geotechnical engineering, 2009, 31(9): 1445- 1449.

[15] 王俊, 方勇, 何川, 等. 盾构隧道施工对砂性地层的扰动及管片受荷特征[J]. 地下空间与工程学报, 2015, 11(1): 156-162. WANG Jun, FANG Yong, HE Chuan, et al. Disturbance of shield tunnel construction to sandy stratum and load bearing characteristics of segment lining[J]. Chinese journal of underground space and engineering, 2015, 11(1): 156- 162.

（编辑：郝京红）

Study on Overburden Load Calculation of Tunnel in Soil Layer

SONG Yi

(China Railway First Survey and Design Institute Group Ltd., Xi’an 710043)

Designing the size and distribution of loads on a segment in the calculation for tunnels is critical. For shallow tunnels in soil layers, the vertical earth pressure is the whole weight above tunnel. However, for deep-seated tunnels in thick soil, the pressure is calculated by the Terzaghi theory, Promojiyfakonov theory or code formula. Some issues exist in selecting a formula. The author compares and analyzes several calculation formula of overlying load in soil tunnels andputs forward a new calculation formula used for vertical load calculation of tunnels in the soil layer. The insights provided from this study can contribute to theengineering design for similar conditions.

soil layer; tunnel buried depth; overburden load; calculation method

10.3969/j.issn.1672-6073.2018.05.015

U231

A

1672-6073(2018)05-0076-05

2017-09-28

2017-11-01

宋艺，硕士，工程师，主要从事隧道及地下工程的勘测、设计及研究工作，281077865@qq.com