基于可变模糊理论的建筑工程造价估算研究

张如好 柳裕政

(1.江苏天舜建设有限公司，江苏 淮安 223003； 2.淮阴工学院，江苏 淮安 223003)

在我国，传统工程项目主要是通过施工图预算和最后的竣工决算来进行工程造价控制，一方面工程造价需要在设计图纸基本完成之后，而且工作量巨大，一旦图纸变更，造价工作又要重头再来；另一方面在工程初期，项目建议书和可行性研究阶段，决策者十分重视投资估算，此时由于缺少必要资料传统造价方法难以运用。随着经济建设的高速发展，建设项目的全寿命周期概念的提出，工程计价贯穿于建设项目各个阶段，在工程项目前期很难根据传统的定额计价和清单计价确定出一个合理、正确、科学的造价。因此工程投资估算作为工程造价中的第一个环节，其地位在与日递增。

由于建筑项目各阶段的造价指标不同，其工程造价的内容和方法也有许多种。施工图设计阶段的预算和竣工阶段的决算往往都是清晰明确的，相比而言项目建议书和可行性研究阶段的投资估算和初步设计阶段的概算具有明显的模糊性、灰色性，因此很多学者将模糊数学、灰色预测模型、大数据和智能算法等方法应用于工程造价估计，显著的减少了计算周期，在工程项目前期为决策管理者提供了有效的途径和有力的支撑。工程造价估算影响因子众多，如何在众多的因子中选取最相关的因子并计算多因子对目标的隶属度是问题的关键，而可变模糊集理论在计算多因子对目标隶属度上具有独特的理论与模型优势，已经在多领域类似问题上得到广泛的应用。

1 可变模糊集理论简介

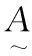
(1)

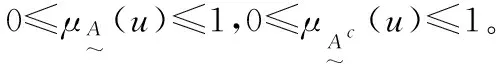
令:

(2)

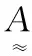
(3)

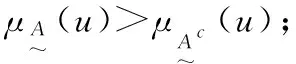
2 基于可变模糊集理论的建筑工程造价估算模型

2.1 指标体系选取和归一化处理

假设已建工程A和拟建工程B的指标体系分别为a和b，二者组成指标体系向量组xij，由于建筑工程不同指标的单位数量级差异较大，在同一模型中无法进行数值计算，首先要对指标体系进行归一化处理。本文中对指标数值越大，造价越高的指标采用式(4)进行处理，对指标数值越大，造价越低的指标选用式(5)。归一化后的指标体系在数值上统一可比对，即指标数值越大，工程造价越高。

(4)

(5)

2.2 层次分析法确定指标权重

对建立的指标体系采用9标度法，将多指标的重要性比较简化为多层次的两两比较，构建判断矩阵，从高层到底层计算判断矩阵的特征根，并检验一致性，最后求出各指标对目标层的权重，即求出指标“重要性”权重w。

w=(w,w,…,wm)=Wi。

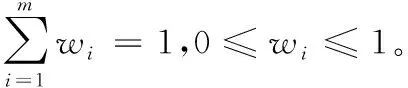
2.3 可变模糊估算模型

应用两级模糊优选模型，得到已建工程和拟建工程各指标的对造价综合贡献相对隶属度uj:

(6)

其中，uj为相对隶属度；α为模型优化准则参数，α=1,2分别为最小一、二乘方准则；p为距离参数，通常可取为海明距离p=1，欧氏距离p=2。

已知已建工程的造价为S，拟建工程的造价S0为：

S0=S×uB/uA

(7)

3 实例与比较分析

3.1 工程基本特征

随着经济社会和城镇化的快速发展，城市多个商圈模式凸显其交通和区位优势，高层建筑作为商圈的核心，其造价估算在区域用地规划中的意义十分重大，造价估算的准确性直接影响项目建议书和可行性研究报告的编制，甚至决定项目能否落地，按计划和设想发挥其区域带动力。本文以某一高层建筑单方造价估算为实例进行研究，已知两栋高层建筑已建工程A和拟建工程B的基本建筑信息情况如表1所示。

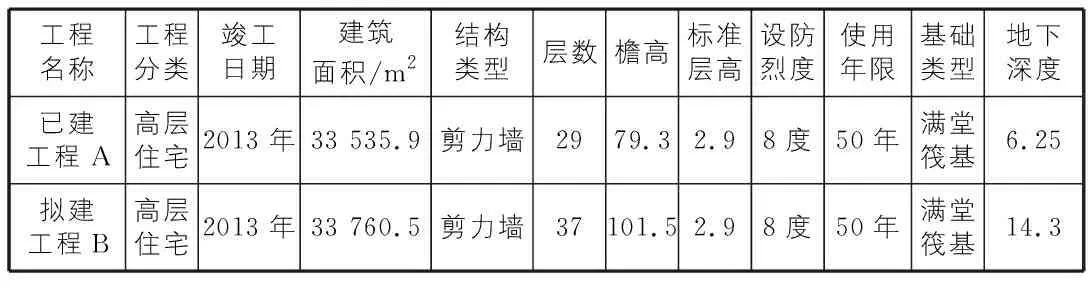
表1 已建工程A和拟建工程B的工程特征

工程造价的估算，涉及因素很多，建筑本身的设计、用途、材料、价格直接影响造价，同时施工企业的技术水平、管理水平、天气、物价波动等间接因素也对工程造价产生一定影响。根据高层建筑特点，选择最相关的因子建筑面积、层数、檐高、底下深度四个参数作为造价估算指标体系。

3.2 建筑工程造价估算

对指标体系进行归一化处理后，采用可变模糊估算模型分别计算已建工程和拟建工程对造价的隶属度uA=0.53和uB=0.47，已建工程的造价S为1 516.75元，则拟建工程的单方造价S0为1 363.42元。

将估算所得数值与建筑工程项目建成后的实际工程造价进行对比,进而验证准确度,如表2所示。

表2 基于可变模糊集理论的建筑工程造价估算模型验证结果

4 结语

由于工程项目规模大，耗费大量人力物力财力，工程项目造价也很大，同时不同类型工程项目，造价也各不相同，且随着建设周期的推移，工程造价也具有动态性。工程造价遍布于建设周期的各个阶段，不同阶段诸如项目建议书中的投资估算、初步设计阶段的概算和施工图设计的预算及最后的竣工决算，是一个逐步深化的过程，不同阶段的工程造价内容、含义和方法均不相同。

随着建筑工程全过程、全生命周期的概念被引入到建筑工程规划、设计、施工、运行中，在工程项目可行性研究阶段就需要对拟建工程进行合理、正确、科学的造价估算，针对工程造价估算的非线性、动态性和模糊性，提出了一种基于可变模糊理论的建筑工程造价估算模型，可以在相似已建工程的基础上，对尚未进行施工图设计的拟建工程造价进行有效的估算，方法简单有效，可为项目建议书可行性研究中的项目投资估算提供有效的支撑，随着建筑信息云数据和云平台的应用，该方法的优势将得到更好的体现。