基岩倾角对边坡稳定性影响分析
吴礼浩尹灵强陆振裕李磊
(1. 江苏省地质矿产局第三地质大队,江苏镇江212001; 2. 江苏地质基桩工程公司,江苏镇江212001)
0 引言
含有基岩的土质边坡是指由强度相对较大的基岩和强度较小的土体覆盖组成的一种混合边坡结构,在我国西北、西南等地区均有广泛的分布。在土质边坡中,边坡的塑性扩展带一般为坡脚与坡顶贯通形成的一条圆弧滑动面,然而在含有基岩的边坡中,由于基岩的存在,使得圆弧滑动面产生变化,塑性扩展带会沿着基岩表面发展。此时,需考虑基岩分布对边坡稳定性分析的影响。
在含有基岩的土质边坡中,常见的破坏类型有:土体整体下滑形成的块状破坏、局部土体破坏形成的弯矩破坏、整体和局部土体都产生一定的破坏形成的块状—弯曲破坏;郭建军、王俊杰等[1]采用极限平衡理论,在Goodam和Bray分析模型的基础上,提出了考虑地下水压力、岩石强度的分析模型,推导出了对应的解析解,并提出了含有岩层的边坡破坏的综合安全系数;刘宏等[2]对缓倾角岩层的边坡失稳破坏模式和稳定性进行了分析,提出了倾倒—崩落、拉裂—崩落和滑落—崩落3种典型的破坏模式,并结合一陡崖边坡工程,对提出的分析方法进行了验证,取得了良好的效果;董金玉等[3]、胡斌等[4]对通过实地勘察,对含有基岩的岩土类边坡的崩塌特性展开了研究,并提出了一定的边坡稳定性分析方法;而后丁秀丽等[5]应用三维数值分析方法,对含有岩层的边坡稳定性进行了分析,获得了含有基岩的边坡塑性区扩展模式;大量的研究说明了基岩分布对边坡稳定性存在影响,然而其影响方式和影响大小尚无准确的分析。因此,有必要就基岩分布倾角对边坡稳定性的影响进行分析。
边坡常用的分析方法主要有极限平衡法和强度折减法。极限平衡法基于极限平衡理论,是工程设计中常用的一种边坡稳定性分析方法,在计算是假定岩体会产生圆弧形、折线形、复合型的滑动面。在滑动面假设准确的情况下可以得出可靠的边坡安全系数;伴随着计算机技术的发展,基于强度折减理论的强度折减法逐渐被设计人员所采用,其具有无需事先假定滑动面,可以较为真实的反映边坡塑性区扩展过程等优势。综合考虑,本文采用基于强度折减法的有限元对含有基岩的边坡稳定性进行分析。
综上所述,本文结合镇江市某边坡工程,采用有限元强度折减法研究了基岩倾角对边坡稳定性的影响,并对塑性区扩展模型进行分析,以期为类似边坡的稳定性分析提供参考。
1 计算理论
1.1 有限元计算理论
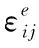
有限元计算过程包括:
1)结构单元离散化,将边坡模型网格化,分解为一个个离散的单元体,并形成对应的单元矩阵;
2)确定单元位移函数,{σ}=[D][B]{δ},其中{σ},[D],[B],{δ}分别为单元应力、单元弹性矩阵、单元应变矩阵、单元节点位移矩阵;
3)采用最小势能原理或者虚功原理,建立单元刚度矩阵方程:
4)将独立的单元刚度矩阵整合成边坡整体刚度矩阵,并将节点荷载或等效荷载添加到刚度矩阵中,建立整体刚度方程:
[K]{Δ}={P}。
其中,[K],{Δ},{P}分别为边坡整体刚度矩阵、边坡整体位移矩阵、边坡综合等效节点荷载矩阵;
5)求整体刚度方程,获得对应的主压应力、拉应力和剪应力。
1.2 强度折减理论
强度折减法具有无需事先假定滑动面形状,能综合考虑边坡土体应力、应变、位移等分布特征等诸多优点。其主要计算特点就是对土体强度参数进行折减,计算公式如下:
c′=c/Fs,
φ′=arctan(φ/Fs)。
强度折减法在摩尔圆中的表示见图1。

当边坡折减的强度线与摩尔圆正好相切时所获得的Fs即为该边坡稳定系数,对应的临界判断标准包括:
1)非线性计算程序不收敛;
2)坡脚发展的塑性区贯通坡顶,形成完整的滑动带;
3)边坡位移发生突变,即位移矩阵产生变异。
本文所使用的有限元MIDAS GTS主要以非线性计算是否收敛为边坡破坏的判断依据。
2 有限元建模
2.1 工程概况
受连续降雨影响,镇江市某边坡出现滑坡现象(见图2),通过地质勘察发现,该边坡为含有基岩的土质边坡。边坡坡底标高6.4 m~7.13 m,坡顶标高39.93 m~51.92 m,边坡最大高度45.52 m,边坡整体坡度50°以上,基岩倾角3°,以该边坡几何尺寸为基础,建立对应的分析模型。

2.2 模型尺寸
为准确分析基岩倾角对边坡稳定性的影响,采用MIDAS GTS对该边坡的稳定性进行分析,模型的计算长度取80 m,坡顶高度取60 m,坡脚高度取20 m,坡体长度取40 m,基岩倾角分别为0°,6°,12°,18°,24°,30°,36°,42°。有限元分析模型如图3所示。

2.3 模型参数
摩尔—库仑弹塑性本构模型[6]可以较好的反映土体的弹塑性本构关系,因此本文中的土体采用弹塑性本构模型;考虑到边坡中的基岩存在一定的纹理特性和分化特点,为较好的考虑土体与基岩之间的相对关系,也采用摩尔—库仑模型模拟基岩。对应的属性参数如表1所示。

表1 土石混合体边坡计算模型参数
2.4 分析模型
基岩较大的强度将会阻碍边坡塑性区的发展,其在边坡中的倾斜角度将会对边坡稳定性产生较大的影响,为量化分析基岩倾角对边坡稳定性的影响,根据基岩在边坡中的倾斜角度,建立了对应的分析模型,见图4,表2。


表2 模型编号
3 计算结果分析
3.1 基岩倾角计算结果分析
对比图5h)与图5a),图5b)的计算结果,可以发现,基岩在边坡中的分布对于边坡原始塑性带的发展路径产生的影响较小,边坡安全系数的变化较小,分别为1.024,1.025,1.031,而对应的基岩倾角分别为0°,6°,12°。当基岩的坡脚增加至18°时,开始逐渐对边坡塑性带扩展路径产生影响,由图5c)可知,基岩的分布使得边坡坡脚的塑性带沿着基岩与土体的混合接触面发展,改变了原本的塑性带扩展路径,间接增加了边坡的抗滑阻力,因此边坡的稳定性得到了一定的提升,安全系数增加至1.053。
随着基岩倾斜角度继续增加至24°(见图5d)),塑性扩展带受到影响的程度越来越大,影响范围增加至1/3的坡高,由于塑性自由扩展路径的改变,边坡稳定性得到了一定的提升,增加至1.072。
当基岩倾角增加至30°时(见图5e)),基岩的分布不仅对塑性扩展路径产生影响,而且对滑体的尺寸也产生了较大的影响。基岩的存在,一方面减少了坡面滑体的体积,直接减少了下滑力;另一方面,沿着基岩与土体接触面发展的塑性扩展带间接增加了土体的抗滑力,因此,边坡的稳定性提升较大,边坡安全系数增加至1.126。
当基岩的倾角增加至36°时(见图5f)),基岩的存在直接改变了原本的塑性扩展路径和滑体的体积。通过分析,发现滑体体积的改变使得边坡稳定性出现较大的增加,安全系数发展至1.195。
当边坡表面仅有少量的覆盖土层时,即基岩倾角为42°(见图5g)),边坡稳定性提高的程度最大。分析原因,基岩的存在,一方面极大的减少了边坡滑块的体积,直接减少了下滑力;另一方面,块石较大的强度,约束了塑性区的自由发展,使其沿着基岩与土体的接触面发展,因而边坡稳定性提升最大,安全系数为1.253。
3.2 基岩倾角对边坡稳定性的影响分析

由图6可知,基岩倾角对边坡稳定性的影响大小随着基岩倾角的增加而增大,其增长关系主要分为三个区间:区间一,基岩倾角为0°~12°,在此范围内边坡的安全系数增加较少;区间二,基岩倾角为12°~24°,在此范围内边坡的安全系数增加较大;区间三,基岩的倾角为24°~42°。
通过分析发现,边坡稳定性变化出现3个典型区间的主要原因与基岩对边坡性分析中的影响模式有关。在区间一中,基岩的存在主要限制了坡脚塑性区的自由发展,且其影响范围仅为坡脚区域,因此基岩对于边坡稳定性的提高效果较小;在区间二中,基岩的存在一方面减少了坡面滑体的体积,另一方面限制了塑性区的自由发展,因而边坡的稳定性有了较大的提高;在区间三中,基岩的存在显著减少了坡面滑体的体积,而且限制了边坡塑性区的发展,因此边坡稳定性提高程度最大。
4 结论
基于不同基岩倾角下边坡稳定性的分析,获得以下结论:
1)在边坡中,基岩的存在将会对边坡稳定性产生一定的影响,其影响性的大小与基岩倾角密切相关,当边坡倾角一定时,边坡的安全系数随着基岩倾角的增加而增加,且增幅变大。
2)通过分析,发现基岩倾角对边坡稳定性的影响主要存在三个典型的区间:区间一,基岩倾角为0°~12°,在此范围内边坡的安全系数增加较少;区间二,基岩倾角为12°~24°,在此范围内边坡的安全系数增加较大;区间三,基岩的倾角为24°~42°。
3)通过对不同倾角下边坡稳定性的分析,发现基岩存在主要对边坡塑性扩展路径和坡面滑体体积产生影响。

