海上疏松砂岩油藏高速开采合理工作制度的研究
王智刚,陈民锋
(中国石油大学(北京)石油工程学院,北京 102249)
油井的合理工作制度包括油井的合理生产压差、抽油井的下泵参数、以及防蜡、防气工艺等方面,其中合理生产压差对海上油田的开发至关重要。目前,油田合理工作制度的确定方法有很多,如系统试井法、地饱压差法、流入动态指示曲线法、临界出砂压差法等,这些方法都是为了确定合理井底流压,进而确定油井合理工作制度。
我国海上油田大多数为普通稠油油藏,储层为疏松砂岩,具有中、高孔渗特征。开采海上稠油要求在投产初期尽可能地放大生产压差来提高采油速度。因此,非牛顿流体高速流动时会不可避免地产生井筒摩阻,造成大量能量损失,影响油井生产能力,此外,疏松砂岩油藏放大压差生产易造成地层出砂,产生附加阻力。
传统确定油井合理工作制度的方法主要关注如何求得合理井底流压,而未考虑海上油田开发易产生井筒摩阻的特点。因此,文本结合实际生产动态特点,考虑了井筒摩阻、出砂、附加阻力等因素,提出了用有效作用压差和极限压差来确定油井合理的工作制度的方法。
1 海上油田高速开采特点及工作制度的确定
1.1 海上油田高速开采特点
我国海上油田一般属于中—高渗、普通稠油、疏松砂岩油藏,大部分采取注水开发,具有见水早、含水率上升快、产量递减快的特点,海上油田的开发具有时效性,一般采取较大的采油速度[1]。海上疏松砂岩稠油油藏在开发过程中容易产生微粒运移及出砂[2]。在水驱开发的早期,随着放大压差生产,油井产液量逐渐增大。在水驱开发的中后期阶段,随着压差继续放大,油田产液能力和产油效率不断下降[3]。海上油田与陆上水驱开发油藏相比,更应注重确定油田合理工作制度。
以渤海油田为例,其中一口典型井的生产动态如图1所示:

图1 典型井实际动态生产状况
1.2 海上油田合理工作制度思路
海上油田在水驱开发早期,放大压差生产可以提高油井产量,但随着压差继续增大,压差和产液量呈非线性关系。由于流体在井筒中流动不仅存在气体或液体与管壁之间的相互作用,气液界面之间还存在质量交换和能量交换[4],流体在井筒中流动时就不可避免地产生井筒摩阻,造成能量损失。因此,确定海上油田合理工作制度的思路如下:
(1)首先要考虑井筒摩阻影响下的油井工作制度。通过选择合适的计算方法计算出井筒摩阻,由于油井产量和生产压差是可以测得的,油田生产过程中实际测量的生产压差为测量压差,所以对比扣除井筒摩阻后的压差和油井产液量的关系。
(2)如果扣除井筒摩阻后的压差和油井产液量呈线性关系,说明井筒摩阻就是造成油井测量压差和产液量非线性的原因;若仍呈非线性关系,则考虑井底污染或出砂等因素造成的附加阻力。附加阻力由油井产能公式计算得出,根据Mohr-Coulomb准则计算出临界出砂压差,通过对比附加阻力迅速变化时对应的测量压差和临界出砂压差,来对前面的猜想进行验证,若附加阻力迅速变化时对应的测量压差大于临界出砂压差,说明此时的压差确实已导致地层出砂,产生了附加阻力。
(3)最后,根据井筒摩阻和附加阻力的变化规律提出有效作用压差和极限压差的概念,根据有效作用压差和极限压差的范围来确定油井合理工作制度。
2 高速管流下井筒摩阻的计算
2.1 井筒摩阻计算方法的对比
井筒摩阻的计算方法较多,目前在压降计算方面有两种方式,一种是以某一标准划分流动型态,然后根据不同流动型态确定气液混合物的密度、空隙率及压力梯度,多采用以试验为基础的经验式或半经验式[5],常见的如Duns-Ros法、Hagedorn-Brown法、Orkiszewski法、Aziz-Govier-Fogarasi法、Beggs-Brill法等[6]。另一种是阻力系数法,将多相管流的各种流动型态反映于阻力系数的规律之中,而不单独地考虑流动型态[7]。
Duns-Ros方法主要适合气液两相垂直管流。其覆盖所有的流动范围,但是主要针对于雾流。在工程上可以达到较高的精度,它更适用于较短的管段,而对深度或压差很大的井,必须进行一连串的分段计算。该法对于低流量的高粘油情况不准确,因此应用于稠油时应注意[5,8]。
Hagedorn-Brown方法主要适合于长管的流动模型,以气液两相滑脱为基础(滑移模型)建立了经验性的相关式。虽然相关式为经验性的,但其在应用中一直有较高的精度,且滑移模型方法在水平多相流动中得到了广泛的应用[5,8]。
Orkiszewski方法把反映两相流动机理的气泡举升速度概念用于油气垂直管两相流压力降的计算方法中,完整地给出了流动形态判别方法,并率先对每个流型单独进行了计算。至此,流动形态模型法作为计算两相流动压力降的方法,在石油工业界的应用已经形成。Orkiszewski方法已被证明是计算两相流压力降的可靠方法之一。
Aziz-Govier-Fogarasi法提出了比Duns-Ros更确切、简单的流动形态分布图。这种分布图流型转变界线明确,有表达式,计算机处理方便。他们对泡状流和段塞流也提出了新的相关规律。当流动型态属于环状流和雾状流时,他们推荐采用Duns-Ros方法。对于过渡型流态,他们建议使用Duns-Ros的内插法[5,8]。
Beggs-Brill法适用于具有任意倾角的管路,目前在倾斜气液两相管流方面比较成熟。但其缺点是对持液率的计算结果偏大,摩阻系数不连续,只预测水平管路的流型,在流型分界处持液率的数值不连续[5,8]。
阻力系数法适用于油、气、水混合物垂直管流,将多相管流的各种流动型态反映于阻力系数的规律之中,而不单独地考虑流动型态[7]。流动型态法中需要根据不同流动型态确定气液混合物的密度、空隙率,而这些参数又是总压力降的函数,有些计算方法还需要查图求解,导致整个计算过程复杂麻烦。阻力系数法克服了上述缺点,计算过程简单,方便。
通过对比,阻力系数法简单、实用,比较适用于油田现场,因此,本文采用阻力系数法计算井筒摩阻。
2.2 基于阻力系数法计算井筒摩阻
Darcy-Weisbach适合稠油非牛顿流体,是计算幂律流体管内紊流摩阻的常用方法,公式如下[9]:

(1)
式中,△Pf为井筒摩阻,Pa;λ为Darcy摩阻系数;L为管道计算长度,m;D为圆管内直径,m;ρ为流体密度,kg/m3;v为圆管内流体的平均流速,m/s。
上式中摩阻系数λ的确定是关键,根据阻力系数法,通过求得平均流速、混合物平均密度和混合雷诺数来计算摩阻系数λ,最后代入(1)式计算摩阻损失[7]。
2.2.1 平均流速
铅直井筒中流体压力是不断变化的,油、气、水混合物的体积流量和平均流速也是不断变化的,根据阻力系数法中平均流速的计算方法有:
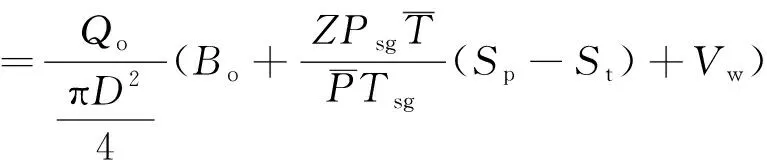
(2)
其中,Qo为产油量,m3/s;Sp为生产气油比,m3/m3;St为溶解气油比,m3/m3;Vw为生产水油比,m3m3;Psg为标准压力,采用98 kPa;Tsg为标准温度,293.15 K;Z为气体压缩系数,无因次;D为圆管内直径,m;Bo为原油体积系数,无因次;T为平均温度,℃;P为平均压力,MPa。
2.2.2 油、气、水混合物的密度
沿整个井筒自下而上,油、气、水混合物的体积流量逐渐增大,但质量流量不变,所以油、气、水混合物的密度是逐渐减小的,根据阻力系数法中平均流速的计算方法有:

(3)
式中,ρo为生产的地面脱气原油的密度,kg/m3;ρng为生产的天然气的密度,kg/m3;ρw为生产的水的密度,kg/m3。
2.2.3 摩阻系数
油、气、水混合物的阻力系数λ与气液两相混合物雷诺数Re2有关,Re2中包含气液质量比的因素,可以通过阻力系数法中的经验公式[7]得到。对于紊流光滑区的阻力系数,我们常用米勒公式计算,其误差要比其他公式要小,米勒公式如下[6]:

(4)
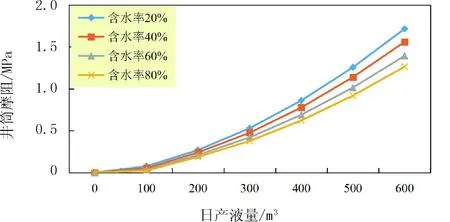
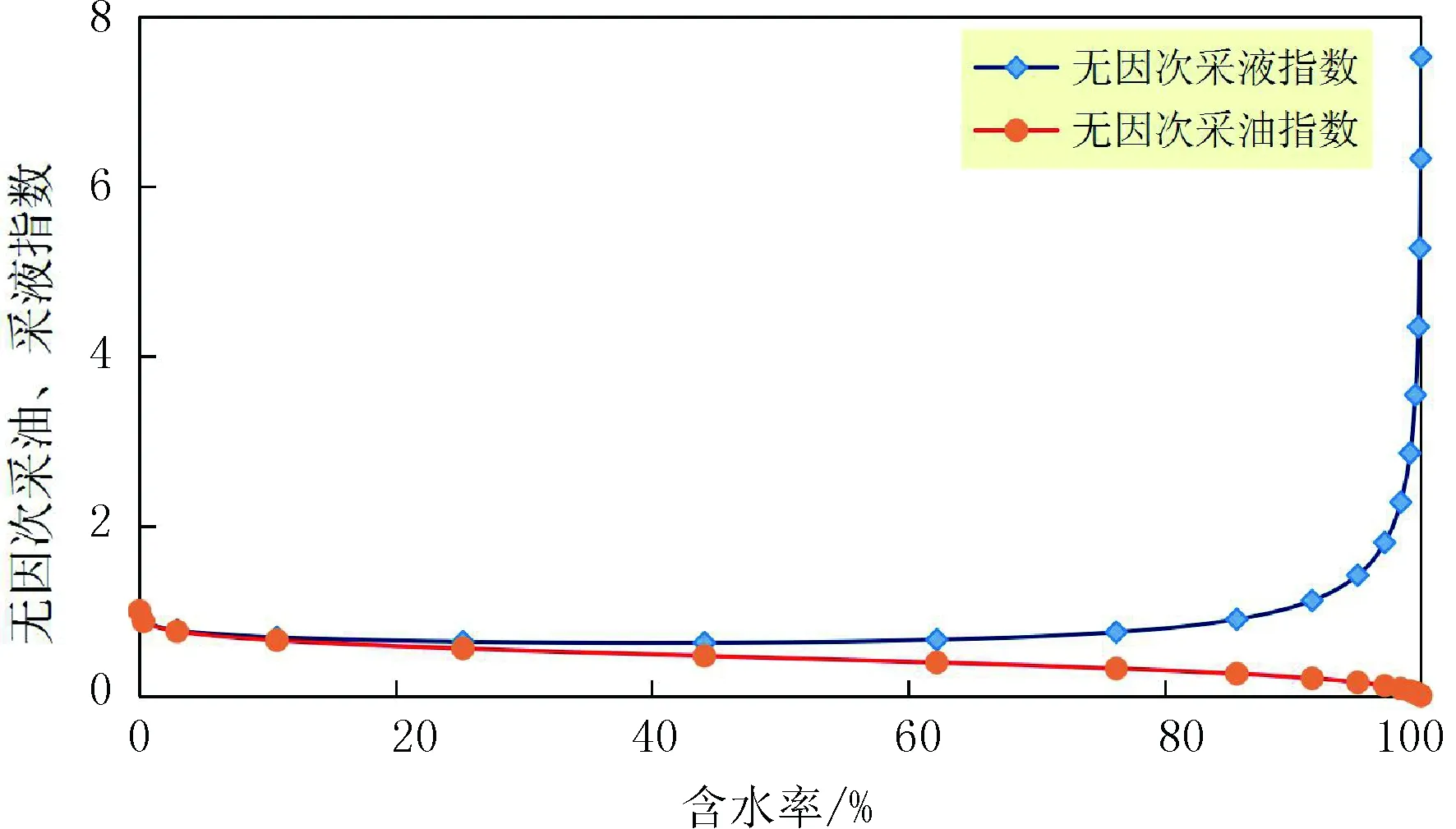
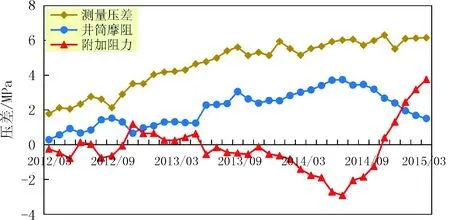
其中,3×103 (5) 以上述典型井为例,其基本参数如下:计算管长深度L=1 200 m,油藏温度T=70℃,油管内径D=62.00 mm,地面原油粘度μo=30 mP·s,地面原油平均密度ρo=962.5 kg/m3,天然气平均密度ρg=0.717 4 kg/m3,油井日产油量Qo=480 m3/d,油井日产液量Ql=600 m3/d,油井日产水Qw=120 m3/d,溶解气油比St=45 m3/d,生产压差为△P=4 MPa。 根据上述的计算方法和基本参数,计算了油井未见水时不同粘度下的井筒摩阻、油井见水后不同含水率下的井筒摩阻(见图2和图3)。 图2 不同粘度下井筒摩阻变化 图2:同一粘度下,油井产液量较低时,井筒摩阻损失很小,油井产液量较高时,井筒摩阻损失较大;同一产液量下,粘度越高,井筒摩阻损失越大。 图3 不同含水率下井筒摩阻变化 图3:油井在产量较低时,如产液量小于200 m3,不同含水率下的井筒摩阻相差不大,同一含水率下,产液量越高,井筒摩阻损失越大。 渤海油田为疏松砂岩油藏,采油速度高,原油具有粘度高、胶质沥青质含量中等、含蜡量低、凝固点低的特点,属于常规稠油,油藏平均孔隙度为26%,渗透率分布范围为(388~1 260)×10-3μm2,属于高孔、高渗油藏。当油井生产压差较大或产液量较高时,地层微粒容易被流体带向井筒方向,造成油层出砂。因此,要对近井地带产生附加阻力的可能性进行分析。 以上述典型井为例,实际井筒摩阻随测量压差的变化规律如图4所示。 图4 E13井井筒摩阻随测量压差的变化规律 从图4可以看出,井筒摩阻和产液量呈正相关关系。产液量较低时,井筒摩阻很小,几乎可以忽略不计,但随着产液量的提高,井筒摩阻逐渐增大。因此,实际作用压差应扣除井筒摩阻。扣除井筒摩阻后的压差变化规律如图5所示。 从图5可以看出,2013年7月之前,扣除井筒摩阻后的压差和产液量的变化规律为基本一致,但后期却不呈正相关关系,说明不断放大压差,除了井筒摩阻的影响外,还有可能由于地层出砂或者井底污染产生了附加阻力。 图5 E13井扣除井筒摩阻后的压差变化规律 附加阻力可以通过油井产能公式来计算。油井产能公式中的压差应为实际作用压差,需要扣除井筒摩阻和附加阻力。附加阻力计算步骤如下:①计算井筒摩阻;②计算油井不同含水率下有因次产液指数;③将井筒摩阻和有因次产液指数代入(7)式计算附加阻力。有因次产液指数和附加阻力的计算结果分别如图6和图7所示。 油井产能公式如下: QL=J1△P实际作用=J1(△P测量-△Pf-△P附加) (6) 附加阻力计算公式如下: (7) J1为油井产液指数,t/(d·MPa);QL为油井产液量,m3;△P实际作用为实际作用压差,MPa;△P测量为测量压差,MPa;△Pf为井筒摩阻,MPa;△P附加为附加阻力,MPa。 图6 不同含水率下的采液、采油指数 图7 E13井附加阻力和井筒摩阻变化规律 从图7可以看出,在2013年7月之前,附加阻力和井筒摩阻很小且变化不大,其影响可以忽略不计;但随着压差继续增大,附加阻力先迅速减小然后迅速增大。因此,实际作用压差应扣除井筒摩阻和附加阻力。 油井产液量与实际作用压差的变化趋势一致。随着放大压差生产,实际作用压差开始增大,但随着压差继续放大,井筒摩阻和附加阻力的影响增大,导致实际作用压差降低,油井产量也相应降低(见图8)。 图8 E13井实际作用压差与产液量的变化关系 附加阻力迅速变化可能是由于适当放大压差会使砂体弱胶结处少量出砂,形成高渗区域,使得附加阻力迅速变小,而当测量压差过大时,会造成岩石骨架大量出砂,堵塞地层,甚至导致地层坍塌,使得附加阻力迅速上升。通过以下计算分析,验证此推测。 根据Mohr-Coulomb准则[10-11],可以计算出油井不出砂最小井底压力,即临界井底流压。对于渤海油田,岩石平均密度按ρ=2.5 g/cm3计算,对于疏松砂岩,取泊松比v=0.13;内摩擦角选取θ=25°;孔隙弹性介质Biot常数β=0.9,上述典型井E13井井深为1 200 m,油藏压力为12.0 MPa。 岩石力学方法计算表明:E13井的临界出砂压差为4.0 MPa。 从计算结果来看,E13井附加阻力开始迅速减小时所对应的压差为4.64 MPa,略大于临界出砂压差,因此,可以说明附加阻力开始迅速减小确实是因为砂体弱胶结处开始少量出砂,形成高渗区域,使得附加阻力大大降低。当压差增大到一定程度时,地层开始大量脱砂,堵塞渗流通道,使得附加阻力显著增大。 为保证油田产量稳定且满足一定的采油速度,油井合理生产压差应保持在有效作用压差和极限压差范围内。在此压差范围内,油层游离砂开始适度出砂,排除了近井地带的污染,显著提高地层渗透性,疏通了流体排泄通道,有利于提高油井产量。当压差超过极限作用压差时,地层岩石骨架开始大量出砂,井底附加阻力显著增加,地层开始出现坍塌,堵塞流体渗流通道,近井地带污染严重,导致油井产量快速下降。 有效作用压差满足以下条件:①油井能有效提液,压差和产量成正相关关系;②井筒摩阻变化平稳,在可以容忍的范围内;③没有明显的附加阻力,地层少量出砂。 极限压差满足以下条件:①压差和产量不成正相关关系,增大压差并不能有效提液;②井筒摩阻达到极大值;③地层开始遭到破坏,井底附加阻力迅速增大,地层开始大量出砂。 综上所述,油井合理工作制度的确定步骤如下:①根据阻力系数法计算油井井筒摩阻;②根据产能公式计算附加阻力;③确定有效作用压差和极限压差,并根据有效作用压差和极限压差确定油井合理工作制度。 以上述典型井为例,分析结果如图9所示。 图9 E13井合理生产压差范围 全区部分油井均出现过大压差生产导致产液量降低的情况。利用上述方法,计算了这些井的井筒摩阻、附加阻力和临界出砂压差,并根据实际开发动态确定了有效作用压差和极限压差(见表1)。 从表1可以看出,渤海油田部分油井的有效作用压差略大于临界出砂压差,说明本文提出的确定油井合理工作制度的方法具有普遍性。 根据表1的计算结果,建议渤海油田的合理生产压差范围为3.2~5.2 MPa。油田部分油井的测量生产压差小于有效作用压差,有进一步放大压差提高产量的余地;而部分油井测量生产压差接近或已超过极限压差,需要加强生产监测,进行及时调整。 表1 渤海油田部分油井临界出砂压差与有效作用压差的关系 (1)海上高速开采状态下,井筒摩阻和附加阻力对油井的产能影响很大。井筒摩阻和产液速度呈正相关关系,附加阻力受压差的影响很大。考虑井筒摩阻后的合理工作制度的确定方法,更加适用于海上油田。 (2)有效作用压差略大于临界出砂压差时,适度出砂有利于油井产量提高;当压差大于极限压差时,地层大量出砂,油井产量迅速降低。油井合理生产压差应保持在有效作用压差和极限压差范围内。2.3 不同条件下井筒摩阻变化规律

3 近井地带附加阻力的确定方法
3.1 近井地带产生附加阻力的可能性分析


3.2 附加阻力的确定方法
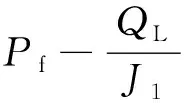

4 合理工作制度的确定
4.1 合理工作制度的确定方法

4.2 方法适应性分析

5 主要认识

