随钻方位电磁波测井反演模型选取及适用性

王磊 ，范宜仁 ，袁超，巫振观 ，邓少贵 ，赵伟娜

（1. 中国石油大学（华东）地球科学与技术学院，山东青岛 266580；2. 海洋国家实验室海洋矿产资源评价与探测技术功能实验室，山东青岛 266071；3. 中国石油大学CNPC测井重点实验室，山东青岛 266580；4. 中国石油勘探开发研究院，北京 100083；5. 中国科学院力学研究所流固耦合系统力学重点实验室，北京 100190）

0 引言

地层界面位置的实时确定是随钻地质导向的关键之一，其对准确钻井与油气产能最大化具有重要意义[1-2]。虽然利用随钻方位电磁波测井响应特征可以定性判断界面位置，但复杂的井下环境导致测井响应极为复杂[3]，井眼到地层界面的定量评价须通过资料的反演处理方可获得。

大斜度井/水平井电测井资料处理通常为复杂的三维（3D）问题，反演时需考虑地层的倾斜度、各向异性及钻井液侵入等各种问题[4-6]。当忽略井眼大小、钻井液侵入且假定地层倾斜方向沿某一方向保持不变时，电测井资料反演可简化为二维（2D）反演[7-8]。但是，电测井3D和2D反演总体仍不成熟，这主要归因于：①井下电测井测量信息数量和种类少，导致3D和2D反演结果存在一定不确定性；②缺乏3D/2.5D正演快速算法；③反演参数过多，Jacobian矩阵计算量大。目前，工业界普遍采用基于滑动开窗的降维处理策略对随钻电磁波类测井资料进行快速处理。Yang等忽略地层横向非均质的影响，基于简化的 3层反演模型消除了视电阻率异常“犄角”[9]。利用同样的反演方法，Li和Zhou实现了邻近地层界面的实时提取[10]。因此，将复杂的3D反演简化为1D问题，可以大大简化反演算法和模型的复杂程度。

随钻方位电磁波资料 1D处理的关键在于简化模型的选取和反演算法的确定。目前，对随钻方位电磁波测井资料的处理仅限于双界面模型，而双界面模型的适用性和单、多界面模型的可行性仍有待研究。一般而言，反演算法的选取依赖于反演模型。梯度类算法具有迭代次数少、反演速度快等优点，被广泛应用于基于双界面模型的随钻方位电磁波测井资料实时处理。但梯度算法的准确性取决于模型的初始值，若初始模型选取不当，则反演结果的准确性难以保证，可能导致地质导向决策失误等问题[11]。相比于双界面模型，多界面模型的代价函数极小值更多，且待反演参数已知信息少，梯度类算法不再适用。随机 Bayesian反演算法具有全局收敛特性、无需计算 Jacobian矩阵等优点，近年来在电测井反演中的应用逐渐增多[12]。目前，随钻方位电磁波测井资料处理一般采用 Gauss-Newton算法，Bayesian反演算法的应用尚未见报道，其收敛性与反演速度等也有待研究。

本文首先介绍了复杂地层模型的反演降维策略和正则化Gauss-Newton算法、Bayesian算法原理；然后，针对降维后的 1D反演问题，对比分析了不同反演模型、反演算法的适用性与反演效果；最后，分别利用优选后的反演模型与最优化算法对现场资料进行处理，取得了良好的应用效果。

1 随钻方位电磁波测井原理与反演降维策略

1.1 随钻方位电磁波测井原理

本节以PeriScope仪器为例，简要介绍随钻方位电磁波测井测量原理。PeriScope包括两类测量信息：视电阻率信息与地质信息（见图1a），前者通过采集轴向发射线圈 T在轴向接收线圈 R1和 R2处激发的电势，并利用（1）式求出两者的幅度比（Att）和相位差（PS）。最后，利用转换图版，将相位差和幅度比转换为视相位差电阻率和视幅度比电阻率。

图1b引入倾斜线圈，线圈法向方向与仪器轴夹角为45°。利用钻铤旋转，测量不同方位角情况下接收线圈处的电势，根据（2）式将信息转化为地下实际地质条件下的相位差和幅度比。该相位差和幅度比包含地层电阻率及界面位置等信息，因此通常被称为地质信息。

图1 PeriScope仪器基础线圈设计

1.2 降维处理与反演模型

在电测井仪器探测尺度下，沿某一方向地层性质可认为保持不变，这样褶皱等地质构造的电磁波测井资料反演可简化至 2D，地层模型如图 2a所示；即认为地层性质沿x和y方向变化，沿z方向同一地层性质保持不变。对2D模型进行逐步开窗处理，将复杂的反演问题转化为一系列的1D地层反演（地层性质仅沿y方向变化，沿x和z方向同一地层性质保持不变）。经降维处理后，反演速度的提升主要来自3个方面：①对每个窗口采用1D解析解可以满足实时正演的需要[13]，每个测量点所需计算时间为10-4～10-3s；②简化后的1D反演模型待反演参数极少；③1D反演过程中，内存等占用量可以忽略不计。对于随钻方位电磁波测井，1D反演模型包括：多界面反演模型（见图2b，地层层数多于3层）、双界面反演模型（见图2c，地层层数为3层）与单界面反演模型（见图2d，地层层数为2层）。

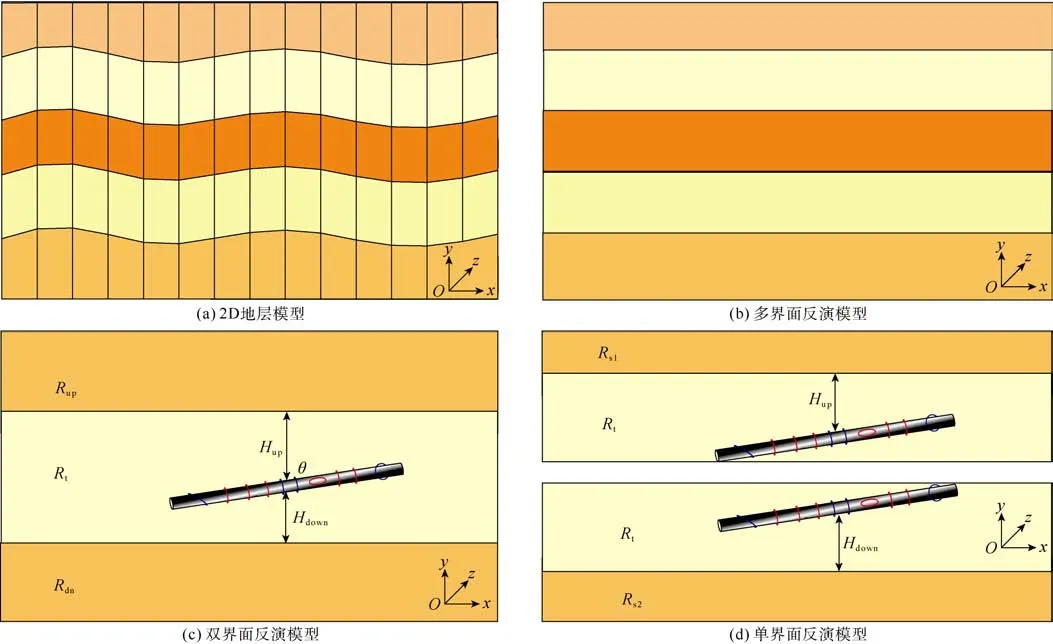
图2 地层反演模型降维处理（图中不同颜色代表不同地层）

2 梯度反演与随机反演方法

本文首先采用常见的Gauss-Newton算法，在代价函数中引入自适应乘子正则化项，以解决传统方法正则化选取困难的问题。同时，为获取复杂模型的全局最优解，引入了随机Bayesian算法。

2.1 乘子正则化Gauss-Newton算法

针对随钻方位电磁波测井资料的非线性反演问题，基于梯度反演方法，第k步迭代时代价函数可表示为[14]：

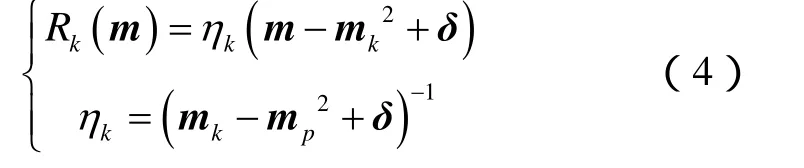
上式中δ为一个定值，其可通过数值实验获取。mp为参考模型矢量，反演过程中可将其设置为上一次迭代时的模型状态，即：

采用 Gauss-Newton最优化方法对（3）式求解，令其对m导数为零，第k次迭代 Ck0∂/∂m= ，得：

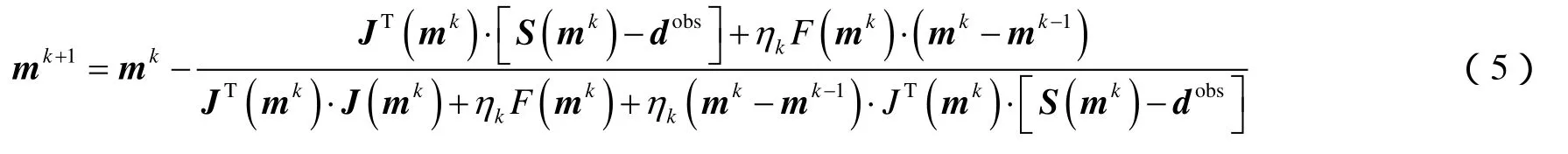
2.2 Bayesian反演算法

根据Bayesian理论，模型解可以看作一随机变量，且满足某一概率密度函数分布，即后验分布。假定先验概率密度满足均匀分布，且似然概率密度函数满足正态分布，则后验分布可由下式表示[12]：

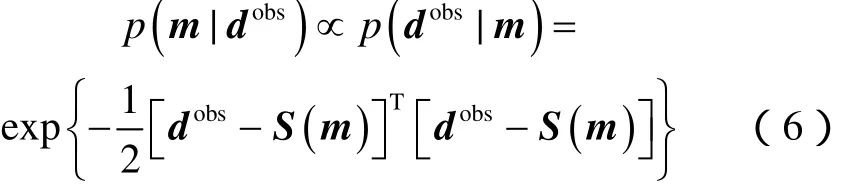
对于Bayesian反演，问题进一步转化为如何高效采样以获取似然函数分布，本文采用马科夫链-蒙特卡洛算法（MCMC）实现上述采样。

MCMC的关键在于构建一条马科夫链，使其满足如下条件：

为满足上式，采用“Metropolis-Hasting”（M-H）算法，引入接受概率函数，以使：

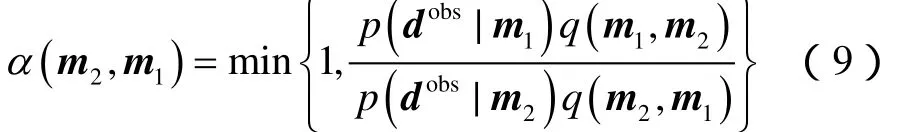
MCMC具体实现步骤如下：根据当前迭代模型m1和转移函数，生成下一候选模型m2；然后计算接收概率并与随机数β相比较，若则返回模型m2，反之返回模型m1，重复上述步骤直至满足终止条件。

3 反演模型与反演算法对比

首先从最常用的双界面模型入手，探讨其适用范围，同时探讨Gauss-Newton和Bayesian反演效果的差异；然后考察单界面、多界面反演的可行性，并与双界面模型的反演效果进行对比；最后，综合反演速度与反演精度，给出反演模型的选取方法。

3.1 双界面反演

图3 层厚为2 m砂泥岩互层模型的PeriScope响应

图4 中间层厚为2.0 m的砂泥岩互层双界面反演模型反演结果

为验证双界面反演模型与反演算法的正确性，建立如图3a所示的砂泥岩互层模型，其中砂岩和泥岩电阻率分别为10.0 Ω·m和1.0 Ω·m。模型最上层和最下层层厚为2.5 m，中间地层层厚均为2 m。仪器自上而下穿过地层时，视电阻率与幅度比、相位差地质信息的响应见图3b—3d，可见在测井仪器穿过地层界面附近时（如图3中虚线所示），其响应值均发生了突变。图4a为采用Gauss-Newton算法反演得到的二维窗帘图，其中每点的颜色表示地层电阻率值，可见在测井仪器穿过地层界面时（如图中虚线所示），其电阻率值发生了明显突变。对比图3a、图4a可知，图4a中电阻率突变点（如图中虚线所示）所对应的界面位置与图3a地层真实模型基本一致，从而验证了Gauss-Newton算法的准确性与双界面反演模型的可行性。值得注意的是，当地层界面距井筒较远时，难以准确重构远处的地层界面，但这并不影响地质导向的进行。二维窗帘图不仅给出了仪器附近地层的上/下界面位置，也直观地初步显示了地层结构分布。图4b为基于Bayesian算法的反演结果，与图4a中Gauss-Newton反演结果相比，Bayesian算法也可准确确定地层界面位置信息（如图4b中虚线所示），但其地层界面处的电阻率有“毛边”现象，稳定性略差。

为研究双界面模型在不同层厚地层的适用性，建立层厚1.0 m砂泥岩薄互层（最上层和最下层层厚为2.0 m），其中砂岩和泥岩电阻率分别为 10.0 Ω·m和 1.0Ω·m（见图5a）。分别利用Gauss-Newton和Bayesian算法进行处理，其反演结果如图5b—5d，可见两种算法均可确定地层界面位置，但在地层界面处电阻率变化的稳定性变差，尤其后者Bayesian算法反演结果“毛边”现象严重（见图中圆圈处）。对比图4和图5可以得到以下结论：①双界面反演适用于层厚大于1.0 m的地层，层厚小于1.0 m时，反演结果的稳定性变差；②Gauss-Newton反演结果略优于Bayesian结果，对于Bayesian算法而言，不断增加采样次数可以提高反演精度。

3.2 单界面反演

为验证单界面反演模型的可行性与适用性，建立5层砂泥互层模型。基于Gauss-Newton算法与基于单、双界面模型，反演后的地层界面位置如图 6所示，图中红、蓝色点分别为双、单界面模型反演地层界面位置。对层厚为3 m的储集层（见图6a），仪器距邻近地层界面距离小于 0.9 m时，单界面反演可获得准确结果。当仪器距邻近地层界面距离大于0.9 m时，方位地质信息受多个界面的影响，导致单界面反演得到的仪器距邻近地层界面距离偏小。随着地层厚度增大，单界面反演结果准确性和稳定性不断提高，地层厚度大于4.0 m时（见图6b—6d），基于单界面和双界面模型的反演结果基本一致（反演得到的地层界面位置基本一致）。一般而言，当储集层厚度大于4.0 m时，基于单界面模型能够准确反演距离仪器 1.8 m范围内地层上、下界面，可以满足实时地质导向的需要。同样也可基于Bayesian算法和单界面反演模型获取与图6一致的反演效果，此处不再赘述。

图5 中间层厚为1.0 m的砂泥岩薄互层双界面反演模型反演结果

图6 单界面模型与双界面模型反演得到的地层界面位置

3.3 四界面反演

在层厚小于1.0 m时，仪器探测范围内可能存在多个界面，过度简化的单界面和双界面模型不再适用。此时，需采用更为复杂的多界面模型方可精细刻画仪器附近的地层界面分布。而模型层数的增加一方面导致反演参数变多，另一方面导致代价函数局部极小值数量迅速增加，梯度类算法不再适用，故在本节中笔者仅考虑Bayesian反演方法。为说明多界面反演模型的优越性，建立图7a所示模型，其中中间层为0.6 m的高电阻率薄层（在测井轨迹上对应的横向距离分别约为135 m和165 m）。分别采用单界面、双界面和四界面模型，反演得到的二维窗帘图见图7b—7d。由图7b可以看出，单界面反演仅能在上、下无限厚地层处获取邻近地层界面位置，难以确定中间薄层的存在（在横向距离135 m和165 m处电阻率几乎无突变）；使用双界面模型时（见图7c），仪器由上而下接近或远离中间薄层时，可得到靠近仪器的一侧界面位置，但仪器在中间薄层时，无法准确确定薄层上下界面位置（在横向距离135 m、165 m处电阻率值突变明显，但135～165 m处电阻率值不稳定）；相比之下，采用四界面反演模型（见图7d），不仅可以给出仪器所在层的上下界面，还能得到邻层界面（在横向距离135 m、165 m处电阻率值突变明显，135～165 m处电阻率值稳定）。以横向距离135 m处为例，经四界面反演后可见在垂直深度1.0、2.3和2.9 m处存在3个电阻率突变界面（见图7d横向虚线），即存在3个地层界面，与图7a中地层界面位置一致。四界面模型精确重构了薄层处地层结构，其可用于储集层结构的精细评价。

图7 四界面模型及Bayesian反演后的二维窗帘图

3.4 反演模型与反演算法优选

反演速度是决定反演模型选取的另一重要因素。Gauss-Newton反演速度主要取决于初始值的数量及迭代次数，而Bayesian反演则是取决于MCMC采样量。对单界面和双界面反演模型，Gauss-Newton算法每个测量点用时分别为0.3 s和3.0 s，而Bayesian需要采样点数分别为5 000和20 000次，每个测量点耗时15 s和60 s。对四界面反演模型，Bayesian需要进行100 000次采样耗时500 s。综合考虑反演速度、反演精度与反演模型最简化的原则，反演模型与反演算法选取可参见表1。

表1 反演模型与反演算法选取表

4 实际资料处理

本节通过图 8所示的某水平井实例说明随钻方位电磁波测井仪器在地质导向中的应用。该水平井可分为 3部分：A段，水平井着陆；B段，水平井钻穿靶层下界面后，调整钻进方向重新钻入砂岩储集层；C段，控制井眼轨迹，使其一直处于目的层内。

若无相位差和幅度比地质信息曲线时，一般利用实测电阻率、岩性曲线与邻近导眼井提取的地层序列进行相关对比，建立地层模型。在A段和B段，基于实时对比结果可以较好地确定地层界面与井眼轨迹的相对位置关系。而在C段横向距离2 455～2 535 m处，随钻电磁波测井曲线出现异常下降（见图8d中两条蓝色虚线间电阻率），仅通过相关对比难以判断低电阻率围岩上下位置，测井解释存在不确定性且钻井时很容易穿出目的层。相比而言，利用随钻方位电磁波测井（见图8a—8c蓝色虚线间测井曲线）可提前预知地层上界面位置（随钻方位电磁波测井值稍变大，远小于钻穿目的层时异常值，说明接近目的层上界面），从而调整井眼轨迹以避免钻出目的层，同时也给出了明确的地层结构分布。

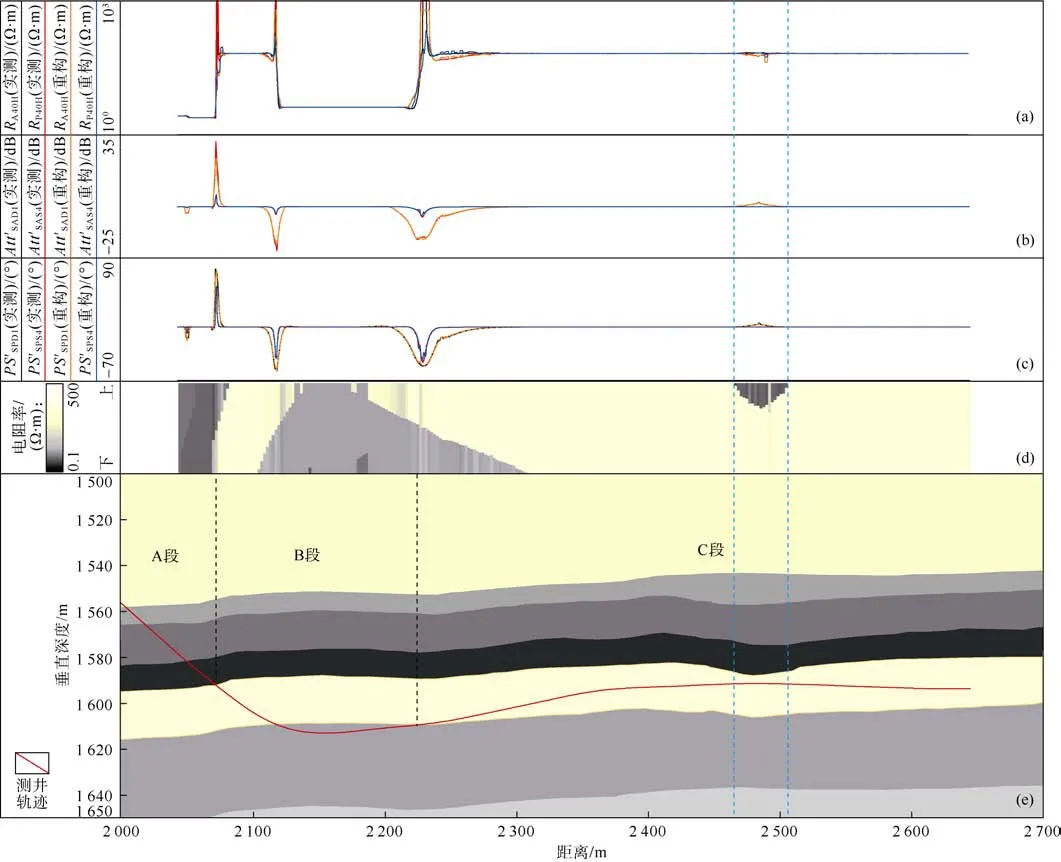
图8 基于随钻方位电磁波测井资料的水平井实时解释结果（图8e中不同颜色代表不同地层）

5 结论

通过降维可以把随钻方位电磁波测井资料 3D反演问题转化为更为可行的1D反演处理，进而实现对地层界面位置信息的实时确定。当靶层厚度大于 4.0 m时，采用单界面反演模型可获取距离仪器最近的地层界面；靶层厚度为1.0～4.0 m时，采用双界面反演模型可获取准确的地层上、下界面位置与储集层电阻率信息；当靶层厚度小于1.0 m时，单/双界面反演模型不再适用，此时需采用多界面反演模型。对单界面和双界面反演模型，采用正则化Gauss-Newton方法即可实现对随钻方位电磁波测井资料的地层界面实时提取，每个采样点反演耗时分别为0.3 s和3.0 s；对多界面反演模型，基于MCMC采样的Bayesian最优化算法可实现地层界面的精细解释，每个采样点反演耗时为500 s。实际资料处理结果表明，基于优选后的反演模型和反演算法可以实现邻近地层界面的精确提取；随钻方位电磁波测井降低了传统电磁波测井水平井解释结果的不确定性，大大提高了随钻地质导向能力。

致谢：感谢美国德克萨斯大学奥斯汀分校 Carlos Torres-Verdin教授在反演算法上的指导，感谢Chevron公司汪涵明博士在方位电磁波测井数据处理过程中提供的帮助。

符号注释：

Att——幅度比，dB；Att′——实际条件下幅度比，dB；Att′SAD1，Att′SAD4——频率 100 kHz 和 400 kHz、源距 243.84 cm（96 in）的幅度比，dB；Att′SAS4——频率 400 kHz、源距 86.36 cm（34 in）的幅度比，dB；——代价函数及其导数；——实测数据；——实测数据与正演响应的L2范数；H——靶层厚度，m；Hup，Hdown——仪器记录点与地层上、下界面的距离，m；Imag——取虚部函数；J——雅克比矩阵；k——迭代次数；m——待反演的参数矢量；m1、m2——任意模型；N——地层界面数；——先验概率密度函数；——似然概率密度函数）——后验概率密度函数；PS——相位差，（°）；PS′——实际条件下相位差，（°）；PS′SPD1，PS′SPD4——频率 100 kHz 和 400 kHz、源距 243.84 cm（96 in）的相位差，（°）；PS′SPS4——频率 400 kHz、源距86.36 cm（34 in）的相位差，（°）；转移核函数；Real——取实部函数；RA28H，RP28H——频率 2 MHz、源距71.12 cm（28 in）的幅度比和相位差电阻率，Ω·m；RA40H，RP40H——频率2 MHz、源距101.60 cm（40 in）的幅度比和相位差电阻率，Ω·m；——自适应正则化项；Rs1，Rs2——单界面地层模型中围岩电阻率，Ω·m；Rt——仪器所在层电阻率，Ω·m；Rup，Rdown——双界面地层模型上、下围岩等效电阻率——正演响应；T——矩阵转置；——同轴发射线圈在两个同轴接收线圈处产生的电动势，——方位角为β1和β2时倾斜接收线圈处的电动势，V；x，y，z——直角坐标系接受概率函数；β——随机数；β1，β2——钻铤的旋转方位角，（°）；θ——仪器与地层夹角，（°）；δ——实验获取初始值。