空气中多杂质颗粒对光传输的影响特性研究
费 莉,黄 颖,赖小龙,刘文晶
(重庆邮电大学移通学院 通信与信息工程系,重庆 401520)
引 言
自由空间光(free space optical,FSO)通信是一种利用激光束作为信息传输的载体,以大气为传输媒介在空间中直接进行语言、数据、图像等信息传输的通信方式,这种通信方式结合了微波通信与光纤通信的特点[1-2]。这种通信方式不需要铺设电缆光缆,易于跨越复杂地形,可以灵活地组成通信网,使一些偏远山区、海岛等地区的用户可以较方便地进行信息交换,是目前通信领域的研究热点。这种通信方式虽然有很多优势,但是在实际运用中也面临着一些挑战,例如:光学探测器的探测效率比低频接收机低;容易受到天气及大气信道的影响等[3-6]。
光束以空间大气为传输媒介,大气特性对光束的传播影响很大,主要包括两种影响:大气湍流运动对光束的扰动;大气分子及悬浮颗粒物对光束的吸收与散射。第1种影响会引起光束的强度闪烁、光束漂移扩展以及产生到达角起伏等现象。第2种影响会导致光束能量损失,即“大气衰减”。第2种影响即光在气体中传播时,如何解决光在与物质作用时的散射问题是光传播问题的核心内容。由此,科研工作者们提出了大量的求解模型及方法。ZHANG[7]等人利用离散偶极近似方法计算了随机取向的火灾烟颗粒分形凝团以及同体积的球形颗粒的光散射Muller矩阵,并对两者的归一化Muller矩阵元素随散射角的分布进行了比较。FAN[8]等人利用经典的T矩阵法和基于扩散限制凝聚理论的广义多粒子Mie散射方法,分析了含多种气溶胶粒子处于1.6μm~2.0μm波段时,非球形单粒子及粒子群的光散射特性,并讨论了粒子有效半径、相对湿度、复折射指数、粒子形状等多种因素对非球形粒子散射特性的影响。HE[9]等人推导了加倍法求解大气矢量辐射传输方程的基本关系式,并利用开发的加倍法解矢量辐射传输方程软件包,生成了海洋水色及水温扫描仪的精确瑞利散射查找表。
然而,上述研究中鲜有给出针对复杂多微粒杂质情况的解决方案。在目前求解光散射问题的过程中,有部分求解方法,包括广义洛伦兹-米理论、有限元法、时域有限差分法、离散偶极子近似法以及T矩阵法[10-16]。在这几种方法中,有限元法在科学研究中广泛应用于多物理场复杂情况的求解,其面对复杂几何结构对场分布求解时表现出的优良性能得到了一致认可[17-20]。
作者基于有限元法,以球体和立方体结构作为研究对象,求解了多种微粒杂质存在的情况,给出了两种基本杂质在光传输过程中的光强分布和变化规律。研究成果从理论上给出了一种解决复杂多杂质微粒存在时的通用解决方案。模型的可移植性强,能推广应用到多个领域。
1 基本原理
运用有限元法求解问题的途径是将待求解域分解成有限个无穷小的单元,设待求解函数为X,则可以得到:
(1)
式中,X′是X的近似值,Ni是每个小单元的个数,Yi是每个小单元的计算结果。将(1)式代入以积分形式定义的标量ω泛函中,可以得到:
(2)
式中,an为ω的元素函数。在此情况下,如果能确定泛函ω的具体形式,则能通过(2)式对规定的函数进行求导,进而对所需的问题进行求解。
2 建 模
出于对光的波粒二象性的考虑,在本次的建模过程中将更多地考虑光的波动性带来的影响。首先考虑光的电场及磁场分布的偏微分方程,并通过设置限制条件可得如下形式的偏微分方程:
▽×(▽μr-1×Ez)-[εr-jσ/(ωε0)]k02Ez=0
(3)
式中,Ez为电场强度,μr为介质磁导率,εr和ε0分别为介质和真空中的电容率,σ为电荷密度,j,k0均为单位矢量,▽为哈密顿算子。此方程即为此次求解过程中需要使用到的散射边界条件,反映了电磁波在某一介质内的强度分布情况。使用有限元方法求解问题的过程如图1所示。

Fig.1 Solving process of finite element method
考虑到模型的复杂程度,在此次的计算中采用三角形剖分的方式分解求解域,假设三角形的3个顶点在平面坐标系中的坐标位置分别为A(x1,y1),B(x2,y2),C(x3,y3),可得公式:
U(x1,y1)=ax1+by1+c=μ1
(4)
U(x2,y2)=ax2+by2+c=μ2
(5)
U(x3,y3)=ax3+by3+c=μ3
(6)
式中,a,b,c为线性系数;μ1,μ2,μ3为3个顶点的线性函数。设置插值算子ξi,ηi,ωi如下:
ξ1=x2-x3,ξ2=x3-x1,ξ3=x1-x2
(7)
η1=y2-y3,η2=y3-y1,η3=y1-y2
(8)
ω1=x2y3-x3y2,ω2=x3y1-x1y3,
ω3=x1y2-x2y1
(9)
将球体和立方体三角剖分以后的结果如图2和图3所示。从剖分的结果看来,由于立方体的形状结构较球体更加复杂,所以在立方体结构复杂的部分需增加更多的剖分单元,以期获得更多更精确的结果。从获得的剖分图也可以看到,在两个微粒杂质边界接触的区域增加了剖分的力度,这部分区域也是本次计算过程中的重点区域。最后可以得到差值方程如下:

Fig.2 Sphere subdivision results

Fig.3 Cube subdivision results
式中,D为差值系数。
3 分 析
通过上述模型的建立,计算了在800nm波长光照射时,有两个杂质微粒同时存在时的情况下,微粒附近的光强分布情况。结果如图4和图5所示。
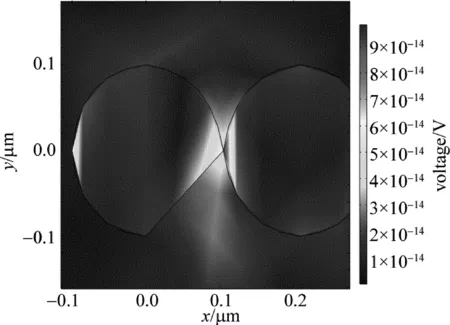
Fig.4 Light intensity distribution of sphere impurity
从得到的结果可以看出,对于结构简单的球体微粒,光波沿其传播的过程中呈现出规律单一的变化,在杂质微粒连接处,光强出现跃变。而对于结构相对更为复杂的立方体微粒,光强分布呈现出了较强的不均匀性,并且由于复杂几何体结构的出现使得穿过立方体杂质微粒的光强强度比球体杂质微粒的光强强度在数量级上多了100倍。

Fig.5 Light intensity distribution of cube impurity

4 结 论
从理论上给出了气体中有多个球体和立方体杂质微粒存在时,光在传播路径上的分布规律。为后续开展涉及光通信研究中的大气衰减理论提供了支持。

