基于模糊层次分析法和TOPSIS法的切削用量选择
贾明刚,汪永超,黄 建,黎方元
(四川大学 制造科学与工程学院,成都 610065)
0 引言
金属切削加工中,刀具的切削用量不仅影响产品的生产效率、加工质量、生产成本,同时也影响着刀具及其他设备的损耗、能源的消耗、机床的噪声、操作的安全性及切削液污染等问题[1]。因此,切削用量的选择对机械加工有着非常重要的作用。传统切削用量的选择往往是通过查阅手册,依靠工人经验和切削实验来确定的,这种方法不能对切削用量进行定量判断和计算,而且忽视了对资源消耗和环境的影响,显然已经不适合现代化绿色生产的要求[2]。如何合理选择刀具切削用量,以提高加工生产率、降低生产成本、减小资源消耗和降低环境污染的影响是我们迫切需要解决的问题。
目前,关于刀具切削用量的选择的研究有很多。例如,张赟等[3]运用粒子群算法选择切削用量;刘伟等[4]运用Pareto遗传算法对切削用量进行优化选择;朱小平等[5]运用多目标粒子群算法对切削用量进行多决策优化研究。这些方法虽然有一定的应用,但是方法比较单一,往往忽略了各要素之间的相互影响作用,也没有考虑到传统切削用量的选择往往是通过查阅手册,依靠工人经验和切削实验来确定的,其结果具有模糊性。
因此本文在前人研究的基础上[6-7],提出了三角模糊层次分析法和理想点法对切削用量选择的方法。利用三角模糊层次分析法[8-9]建立切削用量的选择模型并得到各评价指标的权重值, 利用TOPSIS法对待选切削用量方案进行评价[10],确定出最佳的切削用量。通过三角模糊层次分析法和理想点法得到对切削用量的量化得分,克服了实际加工中根据经验来选择切削用量的不确定性的缺陷,减少了对人为因素的依赖,提高了加工质量并减少对资源消耗和对环境的污染。最后,以阶梯轴在加工过程中的切削用量选择为例,验证了该方法的可行性,从而能够应用于实际生产中。
1 切削用量选择的优化模型的建立
在实际的加工生产过程中,可供选择的刀具切削用量往往有很多种。不同的切削用量对零件加工生产率、加工质量、加工成本以及能量消耗和环境影响都是不一样的。传统的刀具切削用量选择往往侧重于加工生产率、加工质量和加工成本,而忽略了能源消耗和环境的影响[11],显然不符合现代化生产要求。因此,在选择刀具切削用量时要综合考虑多个决策因素[12],然后对各种可选的切削用量进行对比,得出最佳的切削用量,使得零件加工过程的总体性能最佳。即:产品生产率最大、加工质量最好、加工成本最低、资源消耗最小和环境污染程度最轻。但是,这几种影响因素之间相互影响相互制约,不能单一的进行选择,只能根据侧重点的不同对切削用量进行一个综合的评价。结合实际加工生产,本文就以这5个方面对工过程进行综合评价,建立刀具切削用量选择模型,如图1所示。
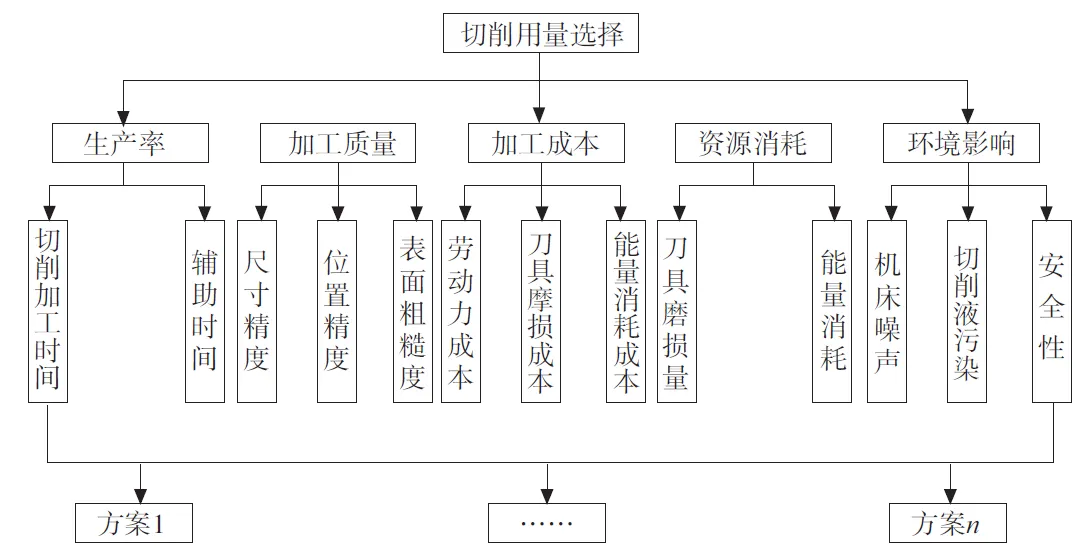
图1 切削用量选择的优化模型
2 模型的求解
刀具切削用量的优化选择是一个基于目标层、指标层、子指标层和方案层的多层次、多指标的决策问题。文章运用模糊层次分析法和理想点法对刀具切削用量模型进行求解。模糊层次分析法侧重于考虑人的主观性和模糊性,分析了目标层各元素的相互重要度,并通过计算权重来确定目标函数对决策问题的影响程度。理想点法通过将待选择方案与理想化的目标进行对比,然后按照与理想化目标接近程度高低进行排序选择出一个最佳方法。利用三角模糊层次分析法建立切削用量的选择模型并得到各评价指标的权重值,再利用TOPSIS法对待选切削用量方案进行评价,最后确定出最佳的切削用量。
2.1 三角模糊层次分析法
2.1.1 三角模糊数
三角模糊数由Zadeh在1965年提出Dev模糊集的概念,是将不确定的语言变量转化成数值量的方法,是为了解决不确定环境下的问题。其定义如下:
定义1:三角模糊数所谓给定论域R上的一个模糊数集是指对任何xR,都有一个数μ(x)[0,1]与之对应,μ(x)称为x对R的隶属度,R称为x的隶属函数。满足式(1)时,称其为一个三角模糊数。
(1)
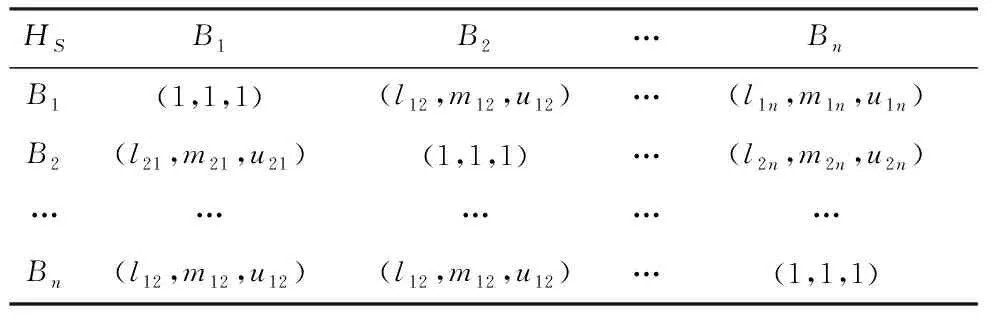
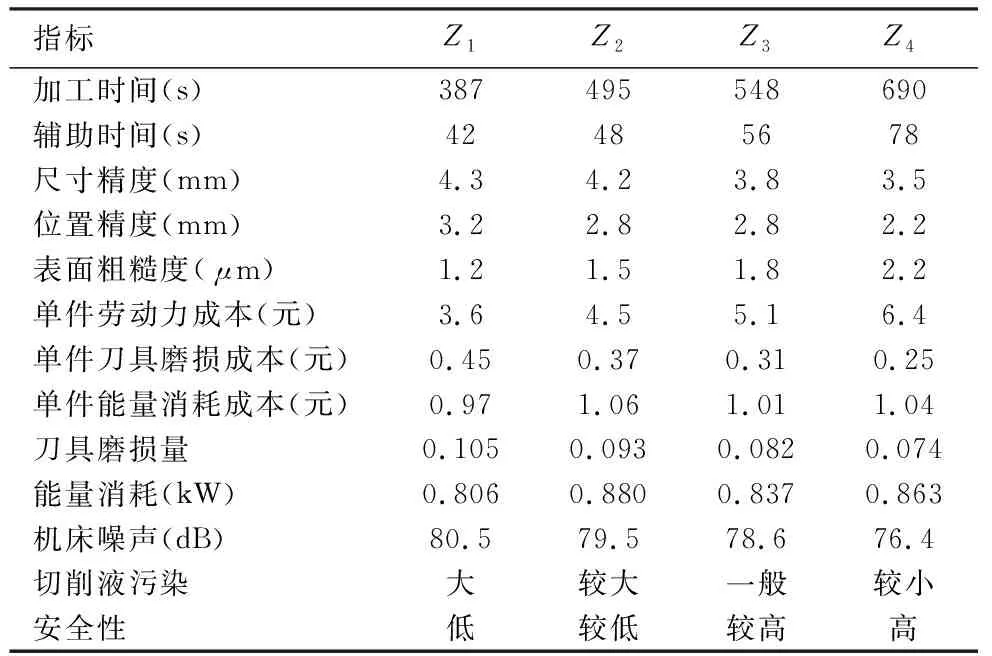
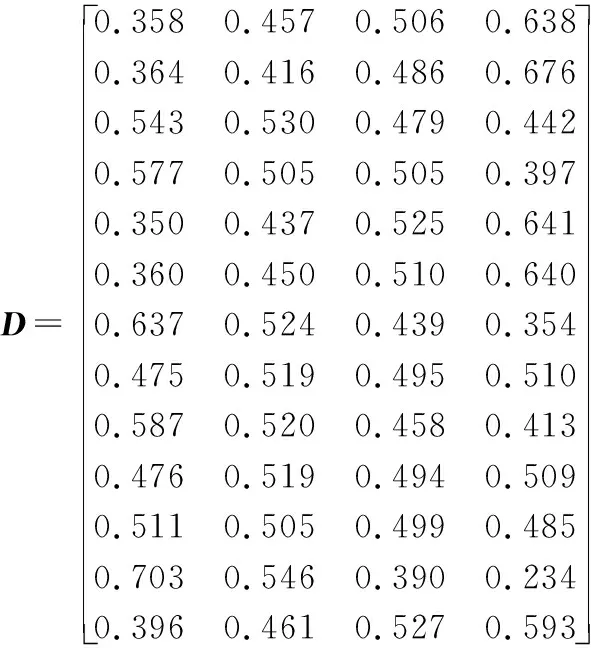
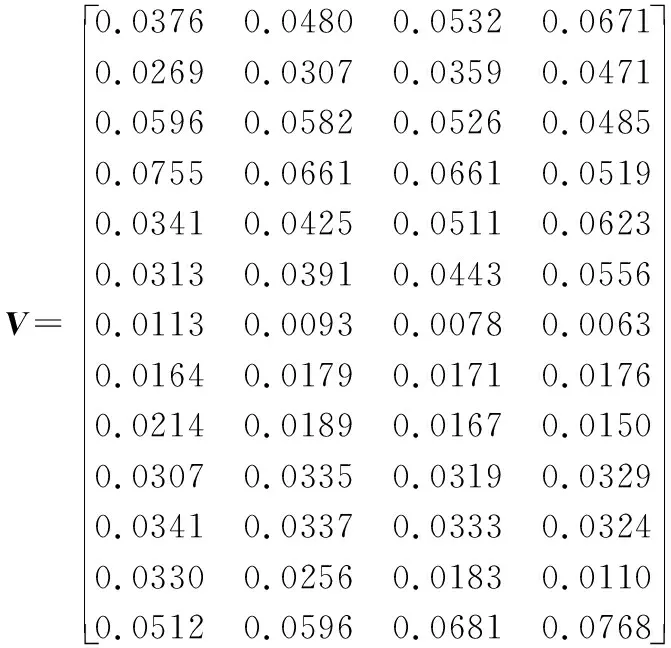
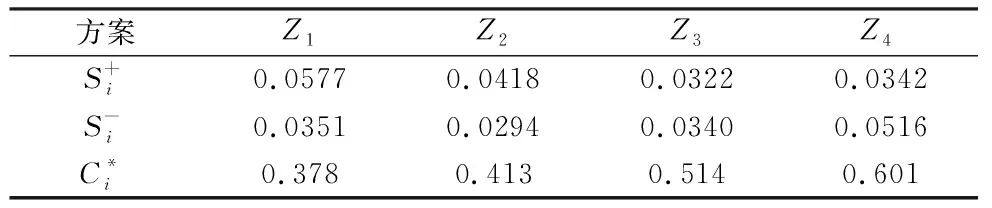
式中,l< 定义2:两个三角模糊数M1=(l1,m1,u1)和M2=(l2,m2,u2)的运算法则如下: M1+M2=(l1+l2,m1+m2,u1+u2) M1⊗M2=(l1×l2,m1×m2,u1×u2) 定义3:M1=(l1,m1,u1)和M2=(l2,m2,u2)是两个三角模糊数,M1>M2的可能度的三角模糊函数定义为: v(M1>M2)= (2) 2.1.2 模糊判断矩阵的建立 模糊判断矩阵的建立是模糊层次分析法中最最关键的部分,它是由专家对各指标相对其他指标的重要程度进行打分得到的。其中HS为上一层的某一个元素,B1~Bn为本层各元素,aij为对于HS而言,Bi相对于Bj的重要程度。构建模糊判断矩阵A=(aij)n×n如表1所示。 表1 三角模糊判断矩阵 (3) (4) (5) 2.1.4 层次单排序 层次单排序是对于上一层某个指标而言,本层次各指标的重要性排序。例如:对于指标层资源消耗而言,子指标层各指标(刀具磨损量、能量消耗)的重要性排序: d(BP)=minν(Sp≥Sj),j=1,2,3…n;p≠j (6) (7) W(k)=(w1,w2,…,wn) (8) 其中,Wi为指标层Bi的权重。 2.1.5 层次总排序 层次总排序是针对目标层而言,本层次各要素重要程度的依次排列。假设层次结构由k个层次,则层次总权重为: W=W(k)W(k-1)…W(2) (9) 通过三角模糊层次分析法确定了指标总权重后,按照公式(10)可构造加权标准化矩阵V。 (10) 理想点法是一种典型的多指标求解方法,通过将待选择方案与理想化的目标进行对比,然后按照与理想化目标接近程度高低进行排序选择出一个最佳方法,与正理想方案最近,负理想方案最远的方案则是最优方案。 2.2.1 构造初始化矩阵 (11) 理想点法进行求解时,首先将各指标进行同趋势化处理,然后将同趋势化的原始数据用公式(12)进行标准化处理。 (12) 2.2.2 构造加权标准化矩阵 由于决策目标体系中各指标的重要程度不同,所以要通过加权予以修正使之可以直接处理。权重大小反映的是决策体系中各指标之间相互重要程度,权重越大表明该指标越重要 。 权重要进行归一化处理使之处于0~1之间,且各指标权重加起来和为1。本文采用三角函数模糊层次分析法来确定各指标的权重。 2.2.3 求正、负理想解 正理想解: V+={(maxVij│j∈J+),(minVij│j∈J-) }= (13) 负理想解: V-={(minVij│j∈J+),(maxVij│j∈J-) }= (14) 其中,J+为效应性指标,J-为成本性指标。 2.2.4 计算距理想点的距离 距正理想解的距离: (15) 距负理想解的距离: (16) 相对接近度表示与理想目标的接近程度,相对接近度值越大则表示其对应的方案与理想方案越接近,该方案越合适。 (17) 某工厂需要加工一批阶梯轴,技术人员在全面考虑了加工工艺流程、机床夹具等设备、刀具型号、切削液、润滑油等一系列问题后给出了4种可行的加工方法Z1,Z2,Z3,Z4。现在用三角模糊层次分析法和理想点法选出最佳的切削用量。 评价小组三位专家分别对指标层指标两两比较判断,采用0.1~0.9标度法对判断结果进行数量标度,并用三角模糊数法表示,如表2所示。 表2 指标层三角模糊数 将三位专家给出的指标层判断结果平均加权处理后,得到指标层三角模糊判断矩阵见表3。 表3 指标层三角模糊判断矩阵 由定义1和式(2)~式(5)可得指标层各指标的初始权重值为: 由式(1)、式(6)将模糊值变为一般的值: d(S1)=minν(S1≥S2,S3,S4,S5)= min(1,1,0.528,0.673)=0.528 d(S2)=minν(S2≥S1,S3,S4,S5)= min(1,1,1,1)=1 d(S3)=minν(S3≥S1,S3,S4,S5)= min(1,0.412,1,0.683)=0.412 d(S4)=minν(S4≥S1,S2,S3,S5)= min(1,0.298,0.825,0.647)=0.298 d(S5)=minν(S5≥S1,S2,S3,S4)= min(1,0.718,1,1)=0.718 故得到指标权重为: W1=(0.528,1,0.412,0.298,0.718) 由式(7)将权重值标准化得到最终权重: 即加工生产率、加工质量、加工成本、资源消耗和环境影响各占的权重分别为:0.179、0.338、0.139、0.101、0.243。 采用同样的方法可得子指标层权重,由式(9)可得层次总权重,如表4所示。 表4 切削用量子指标权重 故得到子指标的总权重为: W=(0.1051,0.0739,0.1098,0.1308, 0.0973, 0.0869, 0.0177, 0.0345, 0.0364, 0.0646, 0.0668, 0.0469, 0.1293) 根据Z1,Z2,Z3,Z4四种加工方法,分别记录了每个方案中加工单件阶梯轴各指标的原始数据如表5所示。 表5 各方案指标原始数据 对原始数据中的模糊化语言进行数值化处理。取(大,较大,一般,较小)=(0.9,0.7,0.5,0.3),取(低,较低,较高,高)=(0.6,0.7,0.8,09),即可得到原始数据矩阵。运用公式(12)将原始数据进行标准化处理得到标准化矩阵D。 其中矩阵D的行分别代表决策目标体系的13个子指标,列分别代表Z1,Z2,Z3,Z4四种方案。 在前文用三角模糊层次分析法得到各指标权重的基础上,用公式(10)求出加权标准化矩阵。 其中,矩阵V的行分别代表决策目标体系的13个子指标,列分别代表Z1,Z2,Z3,Z4四种方案 。 由式(13)、式(14)求出正负理想解V+和V-: V+=(0.0671,0.0471,0.0596,0.0755,0.0623, 0.0556,0.0113,0.0179.0.0214,0.0335, 0.0341,0.0330,0.0768) V-=(0.0376,0.0269,0.0485,0.0519,0.0341, 0.0313,0.0063.,0.0164,0.0150,0.0307, 0.0324,0.0110,0.0512) 表6 相对近似度计算结果 本文综合考虑了生产率、生产成本、加工质量、资源消耗和环境影响这五大影响因素对切削用量的影响,建立了刀具切削用量选择的优化模型。用案例论证了采用三角模糊层次分析法进行刀具切削用量的选择的可行性。最后通过理想点法比较最终刀具切削用量方案与最理想方案的相对近似度,选择相对近似度最大的方案作为最佳的刀具切削用量方案。解决了同时满足多种需求的刀具切削用量选择问题,并通过实例验证了方法的可行性,对今后刀具材料选择问题具有非常好的实用价值。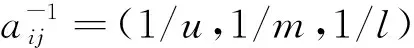

2.2 理想点法
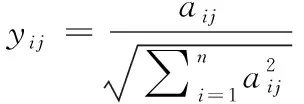
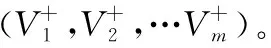
3 案例分析
3.1 确定指标权重



3.2 理想点法评价各指标
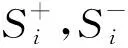
4 结论

