计及风剪效应的垂直轴风力机叶片倾角优化

张立军, 米玉霞, 赵昕辉, 马东辰, 张松, 王旱祥

(1.中国石油大学(华东)机电工程学院 山东青岛 266580; 2.中国石油大学(华东)化学工程学院 山东青岛 266580)

现今清洁能源是世界能源的发展趋势,而风能作为一种清洁可再生能源,其在地球上的可利用的资源比水资源更丰富,共约200亿kW,发电量可达到13 PW·h,且具有地域限制小等优点[1]。随着世界能源需求不断增长,大量的陆地和海上风电场不断开发,风力发电机的功率也不断增大,但风力机受外在因素的影响也在增大,其最直观的结果是使风力机运行不平稳[2]。风力发电机主要是靠叶片进行动力转化,可从风力机叶片研究风力机不平稳运行问题[3]。Thomsen等[4]针对某一特定风力机通过对叶片进行加载直至其破坏,并记录整个过程中位移的变化情况研究叶片在挥舞方向的抗载能力;Sutherland[5]对玻璃纤维的风力机叶片的疲劳性能进行了分析;Veldkamp等[6]对风力发电机的各个部件进行了使用寿命估计和疲劳分析。赵杰等[7]验证了用多个小型风力机取代单个大型风力机可有效减小风剪切的影响;孔屹刚等[8]研究发现随着风力机容量增大,风力机的整体尺寸相应变大,风剪切问题对风力机载荷和功率的影响也不断增大。虽然现今大型风力机多为水平轴风力机,但垂直轴风力机在建造大机型上并不逊于水平轴风力机,甚至更有发展空间[9]。毕长飞[10]提出通过翼型后部加厚的方法来增加风轮叶片的强度,提高其工作稳定性;江成生[11]基于有限元软件ANSYS和Miner准则提出了两种预测叶片疲劳寿命的方法;张婷婷[12]针对某特定风力机,对其叶片采用风力机载荷谱和线性累积损伤法则的叶片疲劳寿命估计算法进行了疲劳分析。而对于风剪切效应的研究,尹伟[13]分析了风剪效应对风力机功率系数的影响;张衡[14]等验证了风剪效应对大型风力机叶片载荷的影响,但在计算载荷时,未考虑来流风速不等于作用在叶片上的诱导风速,上下风区的诱导速度不一致的问题;且计算倾角时,仅考虑了叶片两端所受的切向力,忽略了法向力载荷的问题。笔者研究风剪切问题对叶片载荷的影响,将对风剪切效应下垂直轴风力机运行一周时叶片载荷进行分析,研究倾角优化方法以改善大型垂直轴风力机的叶片受力情况。

1 风剪效应对叶片载荷影响

1.1 风剪效应

风剪效应是指随着高度增加,风速也不断发生变化的现象。风剪效应的主要起因有两个:动力因素和热力因素,第一个是由于地面的摩擦效应,第二个主要与近地层大气垂直稳定度有关[15]。

风速计算方法主要有对数律公式和指数律公式两种。实测表明,这两种计算方法均能较好地反映风剪切效应,但根据对数律计算的风速值与实测值的偏差比用指数律公式计算的风速值与实测值的偏差比大[9]。对风速沿高度的分布用指数律公式表示为

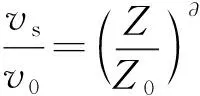
(1)

式中,vs为离地高度Z处的平均风速,m/s;v0为离地参考高度Z0(一般取10 m)处的平均风速, m/s;∂为风速廓线指数。结合某地的气候条件,选取Z0=10 m[13]。

陆地普遍适用的风速廓线指数[16]为∂=0.20,得到风速随高度的变化曲线,如图1所示。由图1可知,在高度大于50 m时,风速增长趋势减缓,在高度10～50 m范围内风速增长趋势很明显。

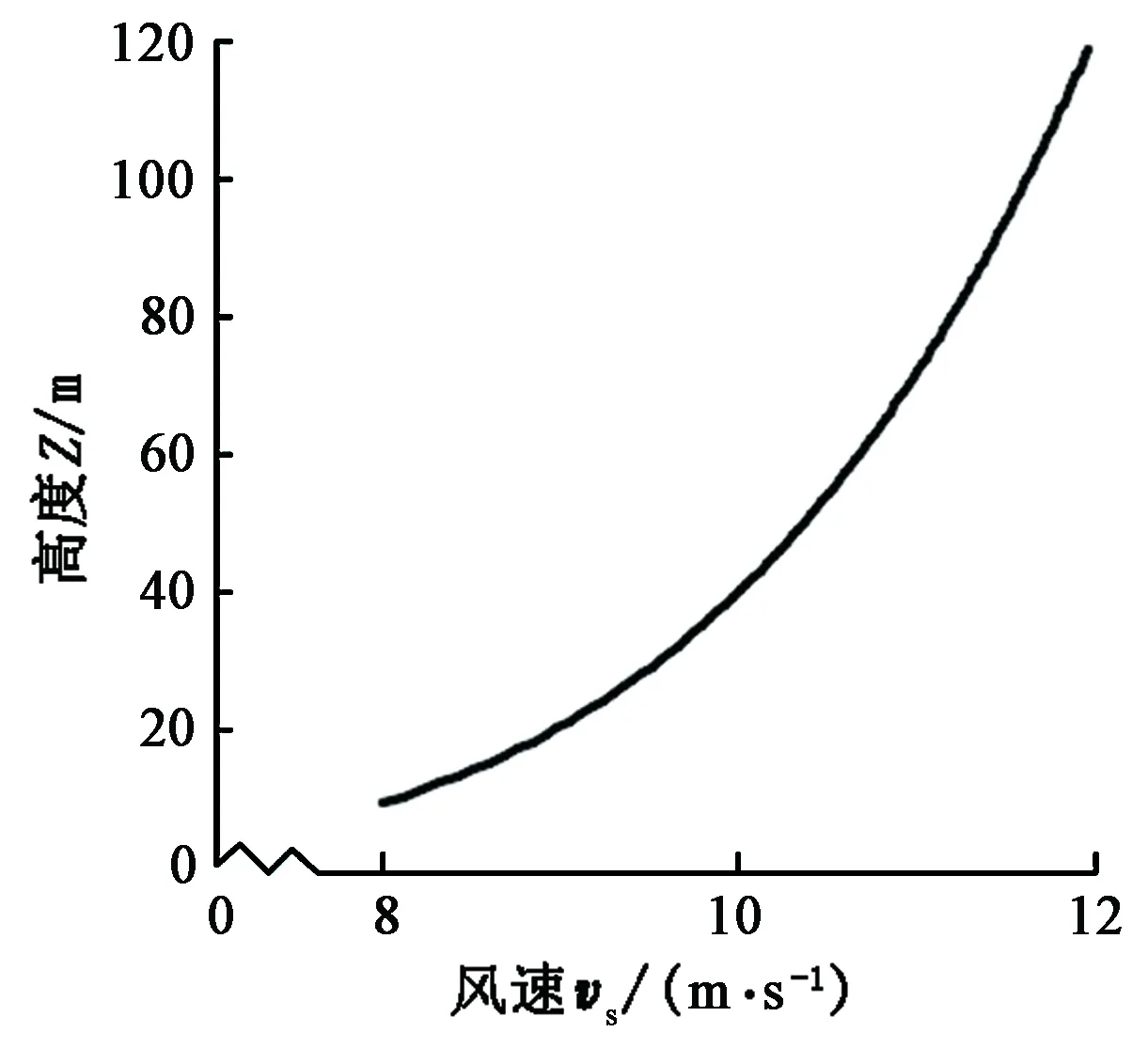
图1 不同高度的风速分布Fig.1 Wind speed distribution at different heights

1.2 模型建立

对叶片进行载荷分析,采用双致动盘多流管模型[17],如图2所示。基于动量方程,假设多个相同的流管通过风机转子,且风通过每个流管作用到叶片翼型上的流向力是相等的,根据上下风区将风力机的转子分为两个致动盘,即第一个致动盘表示上风区中的半个转子扫掠面,第二个致动盘表示下风区中的半个转子扫掠面。采用的流管数为8,流管在垂直方向上的高度为Δh。

对于垂直轴风轮,通过矢量图解法得到一个叶片分别在上风区和下风区的受力情况,如图3所示。图3中,vu和va分别代表垂直轴风轮上、下风区的诱导速度,两者的值均小于来流风速v∞;ω为风轮旋转角速度,ωR为切向风速;W为诱导速度和切向速度的合成风速;α为叶片攻角,是合成风速方向与叶片弦长方向的夹角;θ为叶片方位角,当方位角θ位于0°～180°时,该区域称为风轮的上风区;当θ位于180°～360°时,称为风轮的下风区。

以叶片在上风区为例,分析图3中参数间的几何关系,可以得出垂直轴风轮的叶片攻角α和合成风速W的表达式为

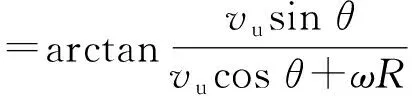
(2)

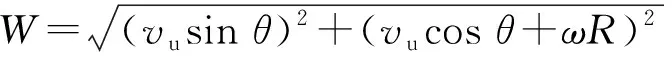
(3)

叶片所受的升力L和阻力D分别为

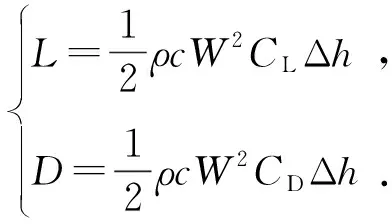
(4)

式中,ρ为空气密度,在标准大气压下取1.247 kg/m3;c为叶片弦长,m;Δh为所研究翼型的某段展向长度,m;CL和CD分别为翼型的升力系数和阻力系数,其值可由NACA系列翼型空气动力学特性数据库查得。

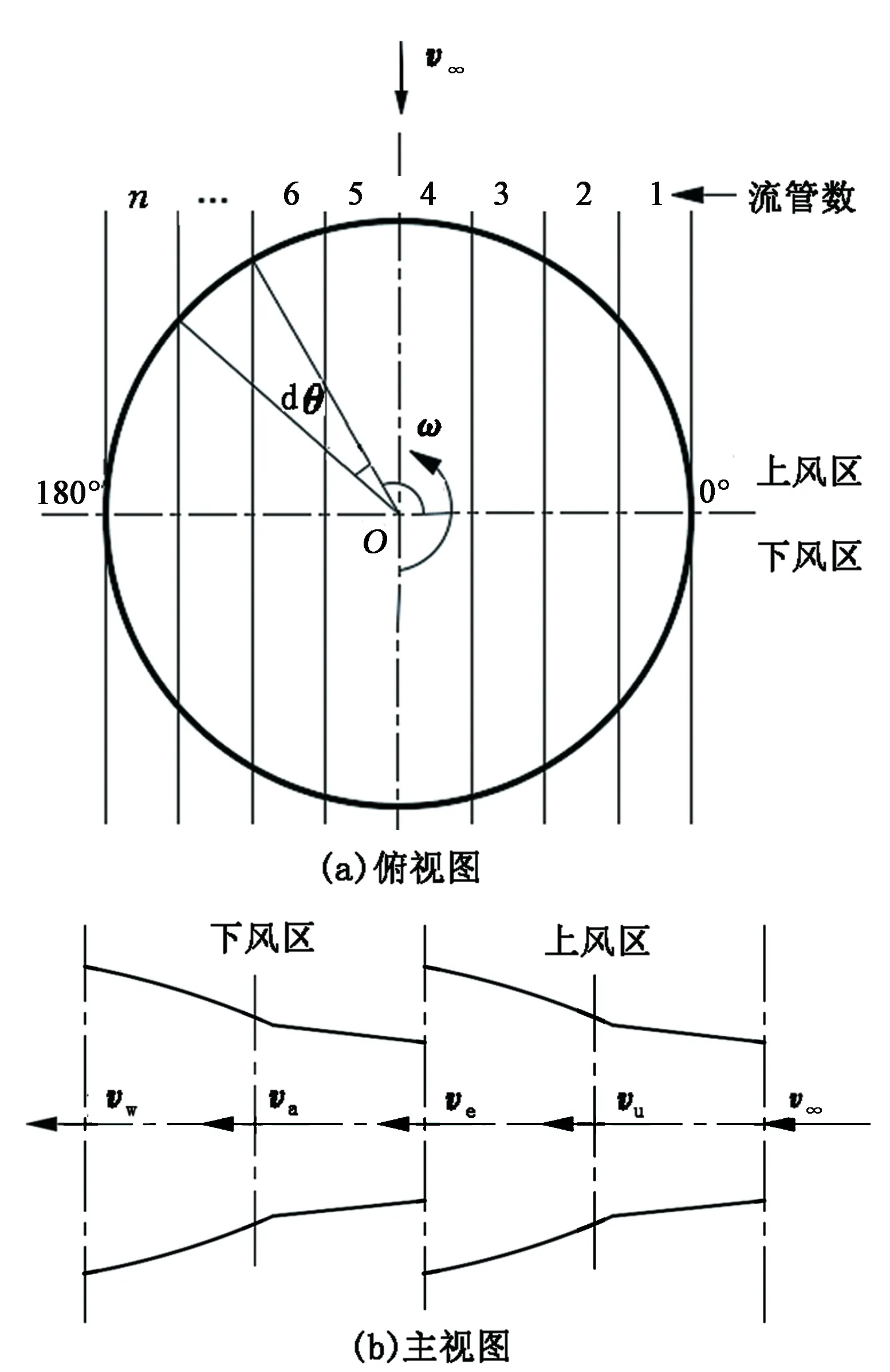
图2 双致动盘多流管模型Fig.2 Double-disk multiple stream tube model

利用图3所示的几何关系,得到叶片切向运动的合力T和垂直叶片切向运动的合力N分别为

T=Lsinα-Dcosα,

(5)

N=Lcosα+Dsinα.

(6)

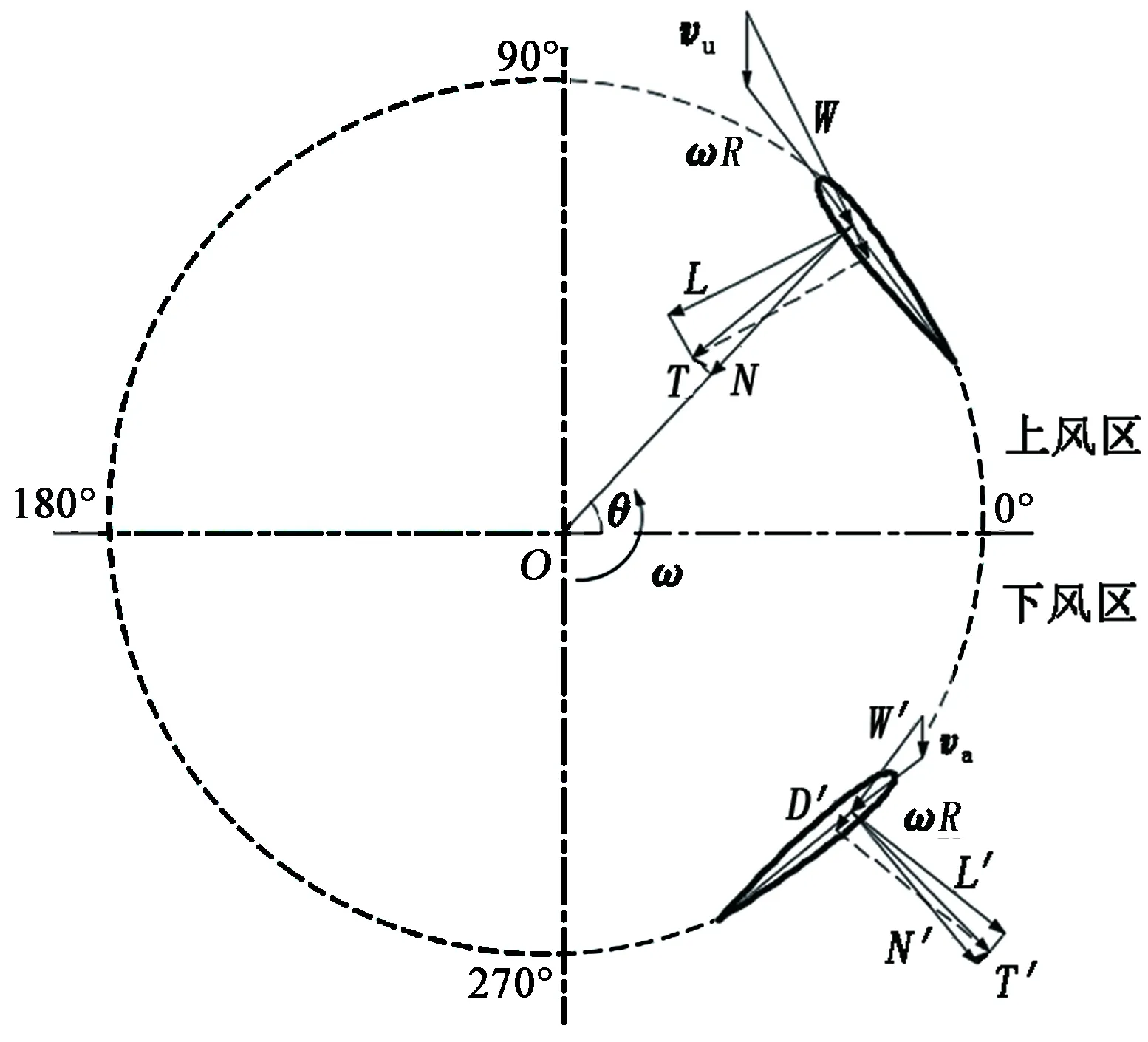
图3 叶片受力分析Fig.3 Blade stress analysis

1.3 载荷分析

研究对象为1.5 MWH型垂直轴风力发电机[13],采用叶片翼型为NACA0015对称翼型,叶片弦长c=3 m,叶片数N=3,风轮半径R=34 m,风轮高度H=30 m。

依照相同功率的水平轴风力机的相关研究,假定叶片底部距离地面为15 m,即对于垂直轴风力机而言,叶片风速、载荷等参数的计算从h=15 m开始。为了计算叶片在风剪切效应作用下受到的载荷,首先计算Δh=0.1 m叶片截段在高度为h=45 m(叶片顶端离地高度)和高度h=15 m(叶片底端离地高度)所受载荷,以分析叶片由于风剪效应引起的在高度方向上载荷不均匀现象。叶片截段在一周范围内所受切向力T和法向力N对比如图4所示,竖线上端和下端分别对应叶片截段的较大载荷和较小载荷,竖线长度代表载荷差值。

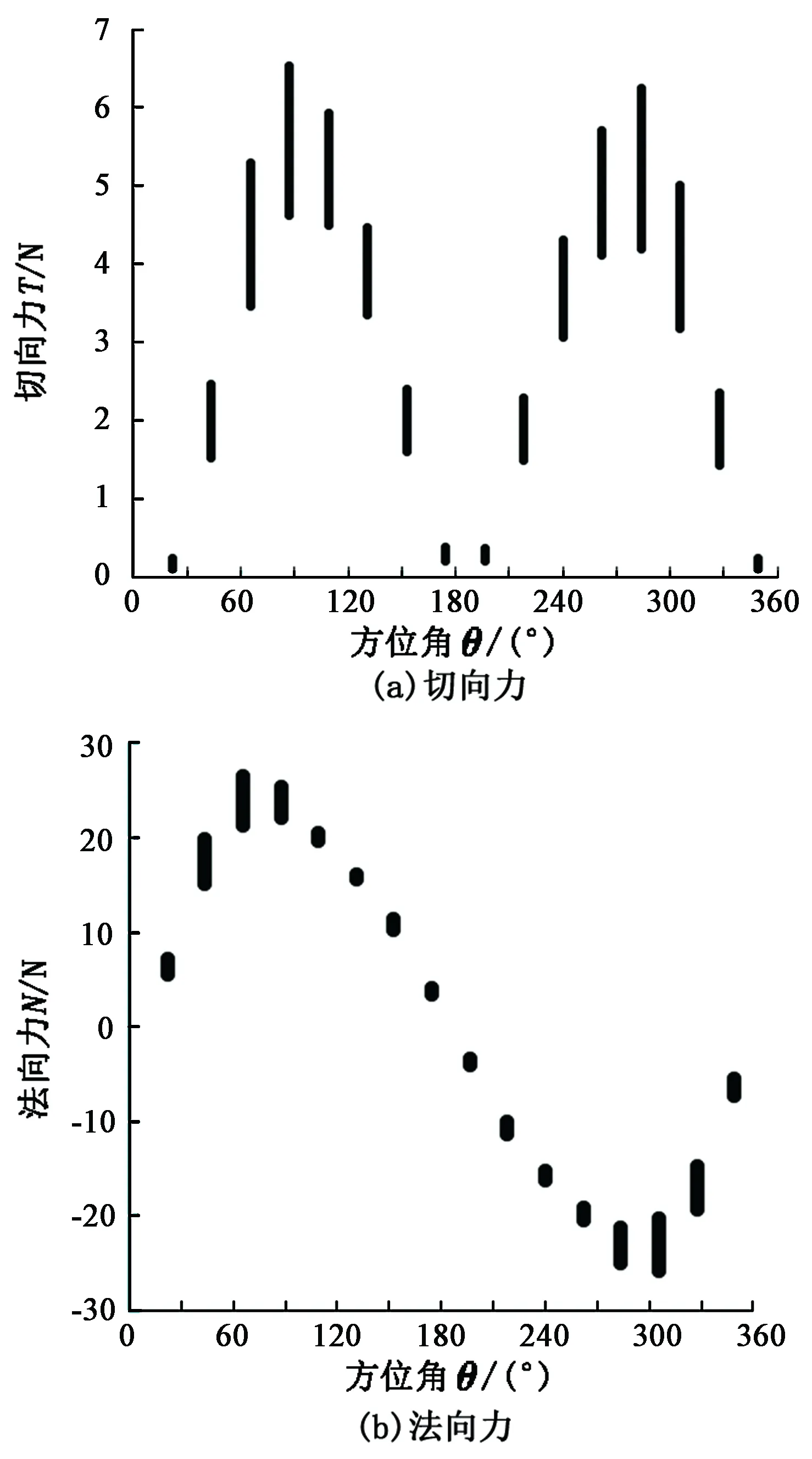
图4 不同高度叶片所受切向力和法向力Fig.4 Blade tangential force and normal force at different heights

从图4可知,每单位长度的叶片在高度为45和15 m处所受切向力相差较小,最大差值仅为20 N;而每单位长度叶片受到的法向力相差值较大,最大差值高达60 N。由图4还发现,考虑风剪效应下,叶片载荷不均匀现象主要体现在所受法向力载荷。

2 方 案

为改善叶片受力不均匀情况,提出了3种垂直轴风轮类型(图5),叶片绕运动切向方向旋转,定义叶片与竖直方向的夹角为倾角β,以逆时针为正,分别对这3种风轮所受的法向力进行对比。以一周范围内叶片上下两端受到的法向力的差值之和为比较依据,研究叶片受力情况随倾角的变化。

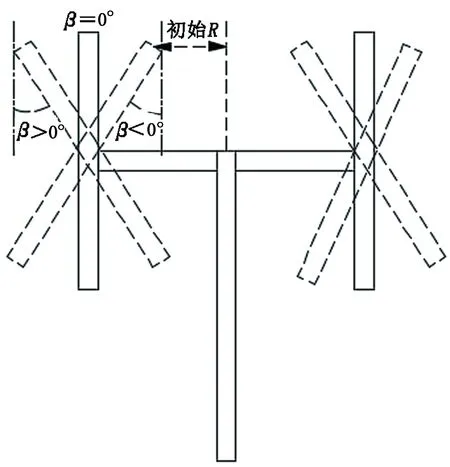
图5 不同风轮类型Fig.5 Different types of wind wheels

对1.5 MW的风力机进行分析,不同倾角下叶片的受力情况如图6所示。可以发现,相对于H型风力机β=0°,倾角β>0°时,倾角越大,叶片上下、两端受力差值之和越大,即叶片受力越不均匀;倾角β<0°时,倾角越小,叶片上下、两端受力差值之和先减小,后增大,即叶片受力不均匀情况先得到改善,后又加剧。

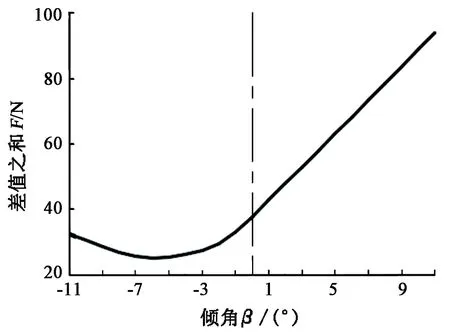
图6 随倾角变化叶片载荷不均匀情况Fig.6 Non-uniform load of with dip angle change

由图6可以判定,针对这一1.5 MW垂直轴风力机,对应的最佳叶片倾角β应小于零,即对应的风轮形状如图5(β<0°)所示。由文献[18]可知,叶片倾角小于零的对应形状的风轮还可有效地改善启动特性。对该风力机整个叶片进行倾角优化,寻找最优叶片倾角,以进一步改善其叶片受力不均匀情况。

3 倾角优化

3.1 优化思路

计算叶片倾角的主要思路如图7所示。以高度h=45 m开始,假定半径R,叶片长度Δh=0.1 m,求得叶片截段受到的载荷;然后在高度为(h-Δh)位置,半径r在(R-Range,R+Range)变化,计算过程中Range=1,在不同半径、高度组合下求出一系列叶片截段的受力N,与上一高度叶片截段所受载荷N0求差值之和的平方,在这一系列中最小差值之和所对应的半径r,即为高度上的最佳半径。再以此为基准,进行下一高度的最佳半径计算,直至高度达到叶片最低端(h=15 m)。对这一系列最佳半径与高度的组合进行数据拟合,求出斜率,即叶片倾角。

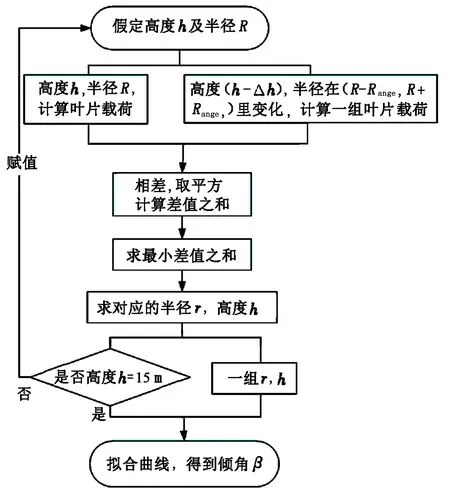
图7 叶片倾角优化流程Fig.7 Flow chart of blade angle optimization

保证倾斜后的风力机与H型风力机的风功率相等,通过不断改变初始半径R(高度h=45 m),计算变倾角后风力机的功率P,与H型风力机功率P0进行比较,直至相等为止,得到叶片的最优倾角。具体计算过程如下。

目标函数:

ΔP=|P(β,r)=-P0(β0,r0)|=0.

(7)

约束条件:15≤h≤45，min(N-N0)2.

目标函数中,β0=0°,r0=34 m。给定一个初始半径r的变化范围,如(R-Range,R+Range),变化梯度为Δr,计算每变化一个初始半径,对应倾斜后的风力机与H型风力机的风功率之差,寻找min(P-P0)对应初始半径r1。启动程序,输入初始半径r,r在(r1-Δr,r1+Δr)内变化,变化梯度为Δr1(Δr1<Δr,缩小半径变化值,提高精度),再计算每变化一个初始半径,对应倾斜后的风力机与H型风力机的风功率之差,寻找min(P-P0)对应初始半径r2,提高精度,直至ΔP=0,得到最优叶片倾角β以及最佳初始半径R。

3.2 计算结果

对该1.5 MW垂直轴风力机进行倾角优化,不断调整输入的初始半径,经过多次迭代,得到计算结果如表1所示。计算结果中,当初始半径精度达到0.000 1时,实际风功率相差值ΔP为0.485 8 W,已近似为零,不必再提高精度。为安装方便,将表1中的最优叶片倾角计算结果圆整为整数,编写MATLAB程序,使风力机倾斜前后的风功率差值等于零,代入最佳倾角,计算出初始半径,从而确定倾角优化后的叶片安装位置。表1中的计算结果是在离地10 m处风速为8 m/s条件下获得,其他风速环境下的优化计算方法与此类似。

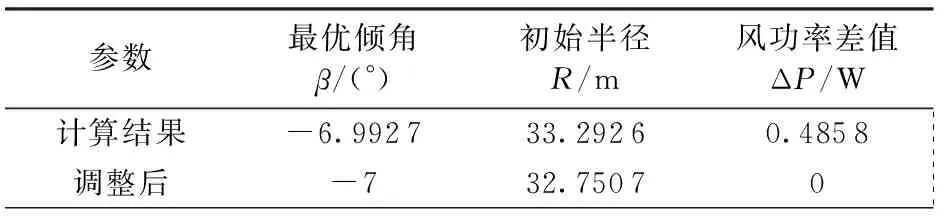
表1 计算结果Table 1 Calculation results

为更清楚地说明叶片的受力情况,引入了方差σ,表示为

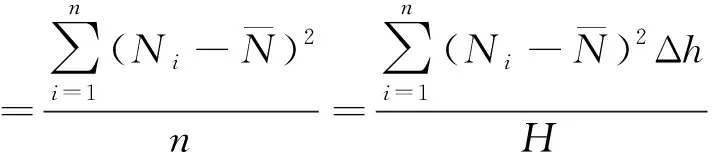
(8)

其中

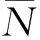
不同方位的不同高度上Δh叶片截段受到载荷的方差可以表征数据的离散程度。不同方位对应的方差越小,说明所受载荷越集中,即载荷相差不大,叶片受力更加均匀;对应的方差越大,说明所受载荷越离散,即叶片在高度方向上受力更加不均匀。验证表1中的计算结果:当倾角为-7°时,叶片在不同方位上受力的对应方差数值在改善前后的对比如图8所示。

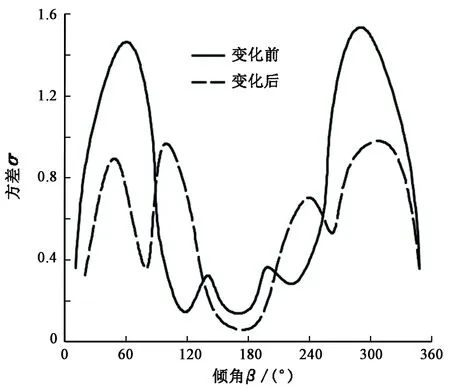
图8 不同方位载荷的方差对比Fig.8 Variance values for different bearing loads

由图8可知,风力机经倾角优化后,其大部分方位的方差均有所下降,且全部方差均小于1;且经过计算,一周范围内经过倾角优化后,方差平均值由0.66降到0.52。这说明经倾角优化后,叶片受力不均匀的情况得到了明显改善。倾角优化后,风力机的形状如图5所示(β=-7°)。由于倾角变化值为-7°,且保证了风功率一致,所需零部件尺寸变化较小,对风力机的经济性影响不大。

4 结 论

(1)风剪效应对叶片载荷影响较大,且影响主要集中在法向力载荷上,所研究的1.5 MW H型垂直轴风力机的单个叶片的法向力最大差值可达60 N。

(2)相对于H型垂直轴风力机,当叶片倾角大于零时,倾角越大,叶片受力越不均匀;当倾角小于零时,倾角越小,叶片受力不均匀情况先得到改善,后又加剧。

(3) 1.5 MW垂直轴风力机在考虑风剪效应下所受载荷均匀时,对应的最优叶片倾角为-7°,初始半径为R=32.750 7 m。

(4)风力机经过倾角优化后,叶片在一周范围内其方差最大为0.96,而原始风力机最大值为1.53,且方差平均值由0.66降到0.52,叶片的受力情况明显改善。