风电出力时序特性及其对省级电网的影响

王羽

（水电水利规划设计总院，北京市 西城区 100120）

0 引言

随着我国风电的快速发展，一方面，由于风电具有随机性、波动性，给电网安全稳定运行、电力消纳等带来一系列问题，增加了电网规划和调度的难度[1-3]；另一方面，由于风电出力在不同的时空尺度上存在着一定的统计规律，通过分析不同时空尺度下的风电时序特性，可以更好把握风电出力对电网调度运行的影响。文献[4-6]分别对东北、甘肃和江苏沿海风电特性进行分析，探讨了风电特性对电网稳定、调频和调峰的影响。文献[7]基于华北地区的风电实测数据，采用统计分析与拟合的数学方法，从相关性和平滑性两个方面研究不同时空尺度下风电波动性的统计学规律。文献[8]基于内蒙电网2年来的历史数据，采用概率统计和序列分析的方法对风电波动特性及出力特性进行分析，对不同容量风电入网对电网有功功率平衡的影响进行了仿真。

上述文献从不同方面对风电出力特性进行了分析，但分析缺乏系统性，没有全面认识到风电时序特性对电网影响，且对风电场群及不同场群之间出力特性的联系缺乏分析，同时也没有基于特性指标分析风电场群与电网运行之间的潜在关系。基于此，本文对风电时序特性进行全面分析，首先建立一套从多角度反映风电时序特性对电网调度运行影响的特征指标，然后根据各风电场的真实出力数据分别从时间和空间角度上分析风电时间序列的规律，最后根据分析的结果评估风电时序特性对电网的影响。本文的研究成果可为系统调度计划的制定提供可靠依据，为风电的长期规划、风电与电网协调发展提供参考和借鉴。

1 风电时序特性指标研究

风力发电受风速、气压梯度力等的影响，其出力具有较强的随机性与间歇性，对电网的调频、调峰、调压等都有较大影响，增加了电网调度的难度，也成为制约风电进一步发展的瓶颈。掌握风电波动性在不同时间、空间尺度上的内在规律，全面细致地把握风电输出功率的变化特性，依据变化特性指导风电运行，在考虑经济和实用性的基础上提升电力系统对风电的接纳能力，是解决大规模风电并网运行难题的关键。

风电出力的随机性是其区别于传统电源的最显著特征。通过分析风电出力随机性的分布特性而掌握其变化规律是研究风电出力特性的基础。

风电场一天中经常出现风速在接近零和额定风速范围内的波动，因此风电出力经常在接近零出力和额定出力之间变化，风电功率波动性强。电力系统每天的负荷曲线都有一个最高的波峰与一个最小的波谷，其差值即为该天负荷的最大峰谷差，简称峰谷差。风电接入系统以后，如果使常规能源机组承担的剩余负荷峰谷差减小，则说明该风电的接入改善了系统运行环境，否则，将加剧系统运行环境的恶化。随着大规模风电接入电力系统，风电的波动特性成为电力系统能否稳定运行的关键因素。

风电场出力的相关性对于风电出力特性有较大影响。相关性越弱，总出力的平滑效应越强，进而可降低系统的备用需求、爬坡速率需求以及输电通道容量需求，对于系统运行的安全性与经济性有重要影响。风电出力之前相关性也是风电出力在空间尺度的重要特性指标，风电出力与负荷之间的相关性又是并网是否友好的关键指标。

因此，本文从风电出力分布特性、波动性、相关性研究风电时序特性，构建一套从多角度反映风电时序特性对调度运行影响的特征指标。

风电具有随机性和间歇性。通过研究风电出力分布特性，可掌握风电出力范围和频率分布，对电力系统调峰和中长期调度计划有重大影响。可用于优化规划设计，量化研究风电送出线路的投资效益，也可用于指导电力系统的调度运行，优化年、季、月长时间调度。

风电波动按时间尺度划分有s级、min级和h级波动；按空间尺度划分则有单机、风场(集群)和区域波动等。风电波动性与具体分析的时空尺度相关，相应的影响范围也有所差异：s级到min级的时间尺度，风电波动主要影响一、二次调频机组的动作，其波动特点为调频机组的选择提供参考信息；h级的风电出力波动，则主要对实时调度或者调度计划的制定产生影响。

风电场出力之间的相关性反映系统对风电的接纳能力。风电与负荷之间的相关性反映风电对系统峰谷差的影响程度，是风电对常规机组调峰容量需求的反映，也从不同空间尺度和不同规模尺度体现了不同的风电聚合效应，可为配置系统备用提供参考。

1.1 出力分布特性

风电出力分布特性用来衡量风电的供电能力。本文针对风电出力分布特性，主要研究的指标如下。

1）风电出力占比(可用率)%η，即实测风电有功功率占额定容量的百分比，表达式为

式中：r()P t为第r个风电场在t时刻风电的实测出力；NP为风电额定容量。

2）风电出力分布特性，即风电出力出现在风电不同出力水平上的概率。令 Pi为风电出力时间序列的出力水平，通常用出力区间表示。 FPi为第i个出力水平的概率，表达式为

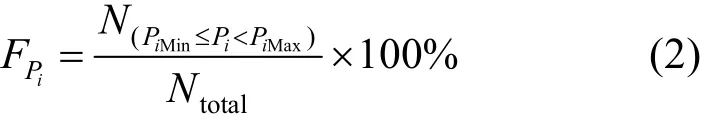
3）风电保证容量[9-10]，是指一定置信度下，风电机组可以替代的常规机组容量的大小。风电保证容量可为电力规划中的电量平衡计算、备用选取、可靠性分析提供参考。设系统包含的常规机组容量为fP，风电容量为WP，等效机组容量为vP，该系统可靠性与常规机组相同。xR表示装机容量为x的系统的某种可靠性指标，表达式为

定义装机容量为wP的风电保证容量为vP。

1.2 波动性

波动性是风电出力最典型的自然特性，研究不同情况下风电波动特性可为电力系统调峰调频、运行控制方式等提供经验和依据。本文针对风电波动特性，主要研究的指标如下。

1）风电波动率。风电波动率是指时间 T内最大值与最小值的差值，若最大值出现在最小值之后则差值为正，为正向波动；若最大值出现在最小值之前则为负向波动。风电波动率表达式为

采用滑窗法计算总长度为n的风电出力波动率的概率分布，以T为时间窗口，以t为滑动步长，得到整个风电出力在单位时间T内所有的波然后对其进行概率统计，其统计方法与1.1节中风电出力概率分布统计方法相同(如式(2)所示)。

2）负荷爬坡/降谷时段的风电波动性。负荷在爬坡/降谷时段，系统中机组的输出功率要紧跟负荷的变化，风电出力的负/正向波动均会对系统调频造成影响，严重时可能会引发频率越限、系统瘫痪等重大事故的发生。因此，研究机组爬坡/降谷时段的风电出力的波动性，可为系统调频计划的制定和调频任务的分配提供可靠的依据。

3）不同风电出力过程的风电波动性。考虑风电出力具有近似的年度的重复性，把风电出力时间序列划分为不同的风电出力过程，本文考虑到所搜集数据的时间尺度并非足够长，将风电过程简化为风电低出力过程、风电小波动出力过程、风电大波动出力过程[11-12]三类。通过研究不同风电出力过程的风电波动率的频率分布，可对风电波动特性进行定性分析。

1.3 相关性

风电场出力之间的相关性除了可以用不同风电场风电出力之间的相关系数表示还可以用同时率来表示，反映系统对风电接纳的程度；风电与负荷的相关性主要用风电调峰作用为指标，反映风电接入前后对系统负荷峰谷差的影响程度。

1）相关性系数是反映某一区域内两个风电场(群)间电力时间序列相关性的指标。如风电场 A与风电场B之间的出力相关性系数表达式为

对于月、年等统计时段，可统计某个风电场相关系数统计区间的概率分布。

2）同时率数值上等于出力之和与装机容量之和的比例，即时刻t的同时率R(t)为

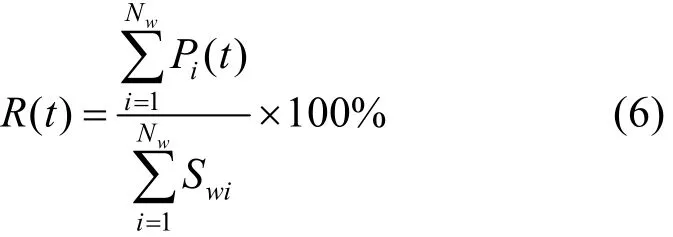
3）风电的调峰特性指标，主要是指将风电作为“负”的负荷计算得到等效负荷，等效负荷峰谷差与原始负荷峰谷差的变化情况。设系统一天之内负荷为 Pli，风电出力为， i= 1,2,3,…,24×60/Δt，等效负荷与原始负荷之间的变化量Pˆ为

ˆP为正时，表明风电接入后增大了等效负荷峰谷差大于原始负荷；ˆP为负时，表明风电接入后等效负荷峰谷差小于原始负荷。通过分析风电接入前后等效负荷与原始负荷之间变化的概率分布可以评价风电接入对系统调峰的总体影响，从而可以判断系统接纳风电的难度。

2 风电出力时序特性分析

本文以东北地区 20个风电场真实出力数据为基础数据进行分析，风电时间序列的采样间隔为15 min。风电场按地理位置可分为A、B、C3个风电场群，在本文所统计的风电场中，A地区风电装机占风电总装机的56.8%，B地区占31%，C地区占11.8%。

2.1 风电出力分布特性

图1为全年风电场群日平均和月平均出力分布图。可以看出，风电场群日平均出力主要集中在装机容量的0～40%范围内，相邻日之间有时会出现较大的跳跃，存在连续数日风电日平均出力较大和连续数日风电平均出力较小的情况。

图1 风电场群日平均和月平均出力分布Fig. 1 Daily average and monthly average output distribution of wind farms

图2为风电场群各月利用小时数及最大出力分布图。可以看出，风电月利用小时数的年内分布有一定的差异，4、5、10、11月的风电利用小时数较大，超过180 h；而7、8月风电利用小时数最低，在 60～90 h范围内；风电场群出力具有典型的季节性，春季(3—5月)、秋季(9—11月)风电资源丰富，风电利用小时数最高，冬季(12、1、2月)次之，夏季(6—8月)最低。

图2 风电场群各月风电发电量及最大出力分布Fig. 2 Monthly wind power generation and maximum output distribution of wind farms

为进一步量化风电场群的风电出力分布，图3给出了负荷高峰时段风电出力累计概率分布图。风电保证容量与风电出力占比相关。由图 3可知，在95%的置信水平下，风电场群保证容量在装机容量的 3%以下，这说明在负荷高峰时段风电能够基本确保提供的容量比例较低。

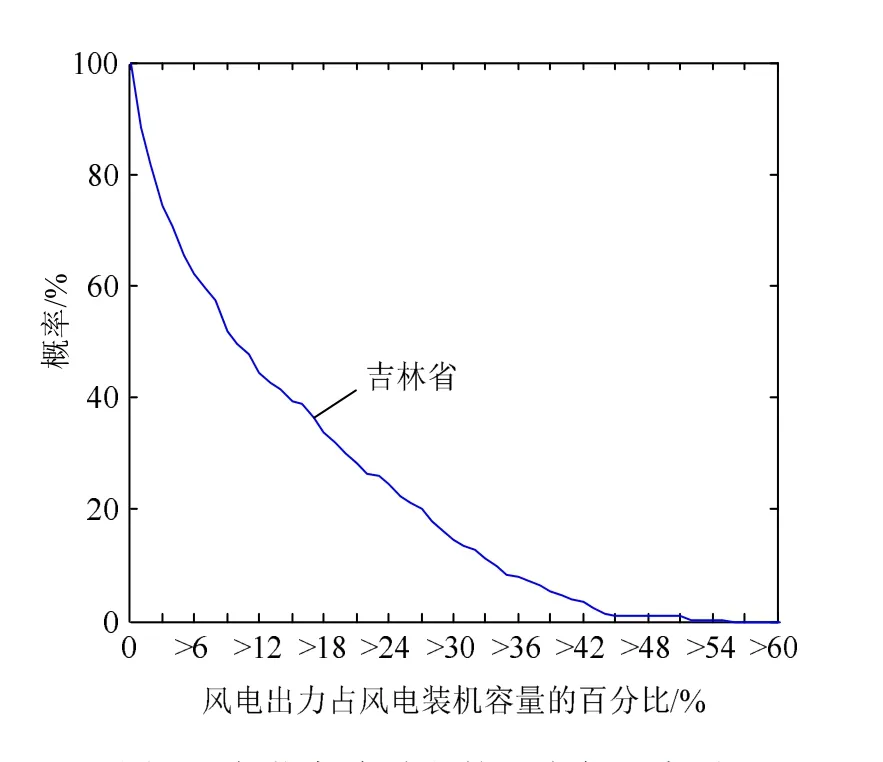
图3 负荷高峰时段的风电保证容量Fig. 3 Wind power guaranteed capacity during peak load hours

2.2 风电出力的波动性

图4 风电波动率的概率分布图Fig. 4 Probability distribution of wind power volatility

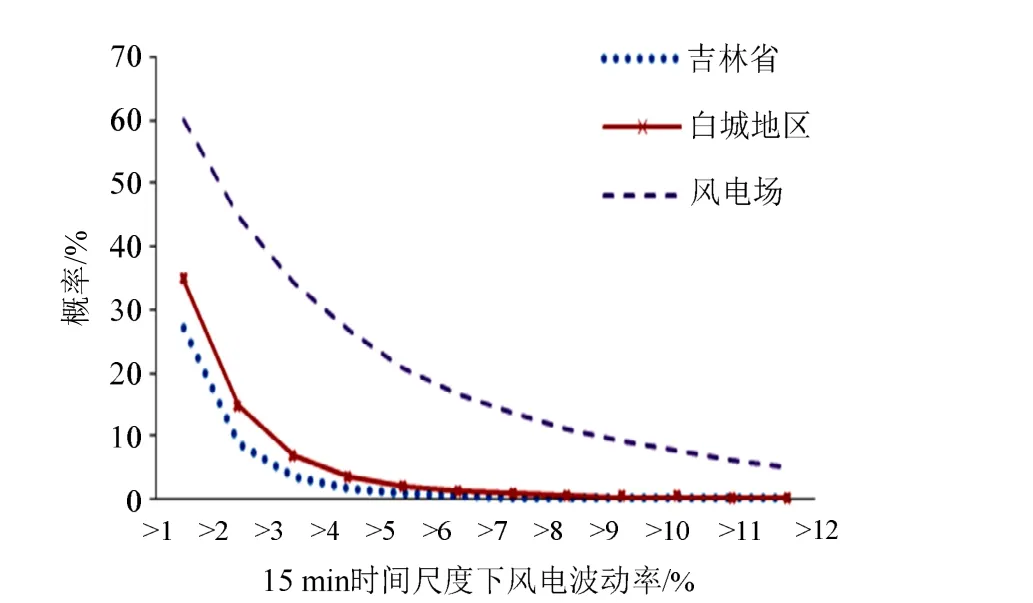
图5 15 min时间尺度下风电波动率累计概率分布图Fig. 5 Accumulated probability distribution of wind power volatility at 15-minite-time scale

经统计，风电场群不同时间尺度风电出力波动近似概率分布和不同区域范围内风电波动累计概率分布情况分别如图4、图5所示。由图4可知，风电出力波动率在-3%～3%范围内的概率如下：15 min时间尺度下为95.76%，1 h时间尺度下为69.76%，4 h时间尺度下为15.95%，24 h时间尺度下为0%。15 min和1 h时间尺度下波动率在-3%～3%之间的概率值最大；4 h时间尺度下波动率在-12%～-9%和0～3%之间的概率值最大，分别为 10.54%和 11.48%；24 h时间尺度下波动率在-30%～-27%和-36%～-33%范围内的概率值最大，分别为8.94%和7.40%；随着时间尺度增加，风电波动率的频率分布从“窄而高”变得“宽而矮”，即波动明显加剧，风电正反向波动出现的概率始终维持基本相同。

从图 5可以看出，某风电场风电出力在15 min时间尺度下的波动率大于 1%的概率为60%，A地区为34%，而3个场群则为27%，随着统计区域的扩大，风电出力的平滑性增加，波动减小。

图6 各风电出力过程持续时间及15 min时间尺度下的波动率累计概率分布图Fig. 6 The cumulative probability distribution of volatility in the duration of each wind power output process under 15 minute-time scale

图6为风电场群各风电出力过程持续时间和15 min时间尺度下波动率的累计概率分布图。由图 6(a)可以看出，风电场群风电大波动出力过程的持续时间集中在24～204 h内，小波动出力过程集中在0～108 h内，低出力过程集中在0～48 h内；其中，大波动出力过程持续时间大于24 h的概率为100%，小波动出力过程为20.73%，低出力过程为16.26%。由图6(b)可以看出，大波动出力过程的在15 min时间尺度下的波动率大于1%的概率值为 37.67%，小波动出力过程为 28.60%，低出力过程为2.54%。

为评估风电波动紧跟负荷的变化程度，图 7给出了风电场群各月份负荷爬坡/降谷时段风电发生正/负向波动的概率图。由图7可知，负荷爬坡/降谷时段，风电发生正/负向波动概率曲线均集中在 50%左右。其中，对于负荷爬坡时段，5月份风电发生负向波动概率明显大于正向波动的；对于负荷降谷时段，3、6、10月份风电发生正向波动的概率明显大于发生负向波动的；降谷时段风电出现正向波动的概率大于爬坡时段出现负向波动的概率。

图7 负荷爬坡/降谷时段风电出现正向/负向波动的概率Fig. 7 Probability of positive/negative fluctuations in wind power during load climbing/falling

2.3 风电出力的相关性

不同风电场出力之间的相关性反映风电场之间出力变化趋势的一致性。以3个临近风电场为例，2月 6日—13日各风电场出力曲线如图8所示，可以看出3个风电场出力变化趋势相近，具有很强的相关性。

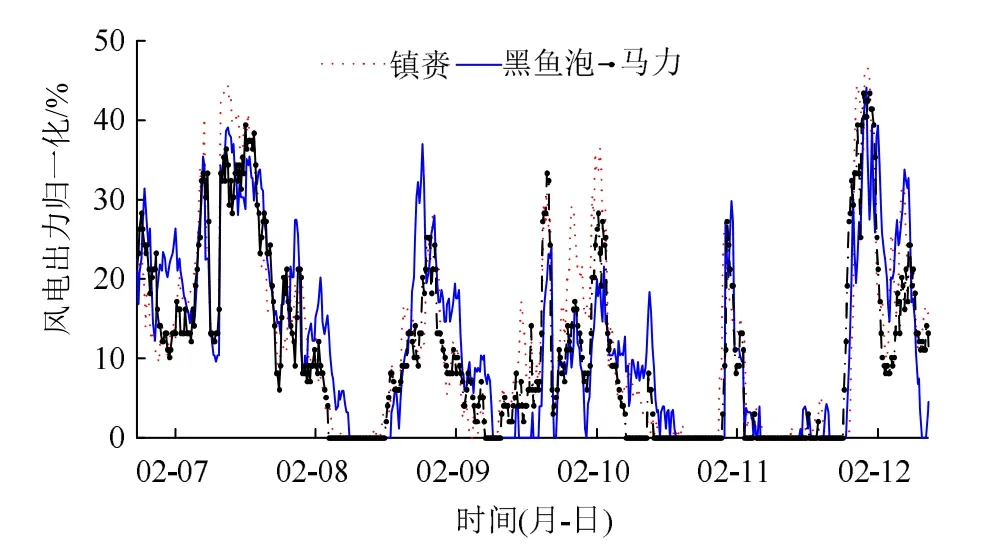
图8 各风电场风电出力曲线Fig. 8 Wind power output curve of each wind farm

表1为各风电场出力之间的相关系数。其中，1号风电场位于C地区，2号风电场位于B地区，3号风电场位于A南部地区，其他风电场位于A北部地区。以6号风电场为例，6号与1号最远，相关系数为0.01，随着风电场之间距离的减小，风电场之间的相关系数在增大，6号与5号最近，相关系数为0.82。

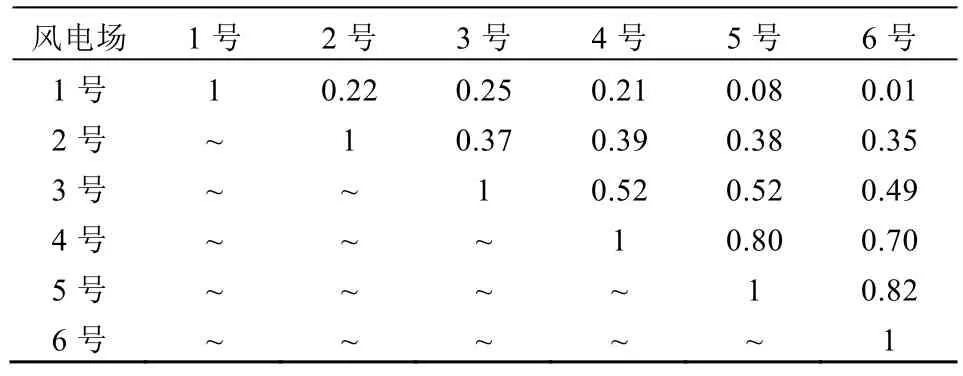
表1 风电场出力相关系数Tab. 1 Wind farm output correlation coefficient

将风电作为“负”的负荷计算得到等效负荷，分析风电场群接入省级电网后前、后，原始负荷与等效负荷峰谷差之间的变化情况，结果如图 9所示。从图中可以看出，风电接入后，等效负荷峰谷差大于原始负荷峰谷差的概率超过60%，峰谷差率增大的概率为70%，其中，峰谷差最大可增加1000 MW。因此，风电场群出力具有明显的反调峰作用，给系统调峰带来了较大压力。

图9 风电接入前/后，原始负荷和等效负荷的峰谷差、峰谷差率之间变化情况的概率分布图Fig. 9 Probability distribution of the change of peak-to-valley and the peak-to-valley difference between the original load and the equivalent load before and after the wind power is connected

3 风电出力对省级电网的影响

3.1 风电对调频的影响

根据 2.2节风电波动性的统计结果可知，在15 min时间尺度下风电场群风电波动率-6%～6%范围内的概率值为99.55%，考虑到风电场群风电装机容量为3298 MW，风电波动引起系统负荷变化率小于 1.02%/min，所以在短时间尺度下风电波动不会给系统的频率调整造成重大影响。分析风电在负荷爬坡和降谷时段的波动特性可知，风电各月份发生正负向波动的概率均集中在50%，只有个别月份的风电会在负荷爬坡/降谷时段出现比较明显的负/正向波动，且风电在短时间尺度下波动幅度小，所以当系统中风电装机容量在一定范围内时，风电波动对机组在负荷爬坡/降谷时段的频率调节影响不大。因此，当省级电网的风电装机容量的比例在一定范围内，在短时间尺度下风电波动的调频需求并不大，可由机组的一次、二次调频完成。

3.2 风电对调峰的影响

根据 2.3节风电接入前、后，原始负荷与等效负荷峰谷差的统计结果可知，风电接入后等效负荷峰谷差大于原始负荷峰谷差的概率为60%，最大可使等效负荷峰谷差增加1000 MW，风电反调峰特性明显。省级电网直调装机以火电为主，水电比例极小，电源结构不合理，缺乏灵活调峰电源，大规模风电接入后增加了电网的调峰难度，冬季供热期负荷低谷时段风电几乎没有发电空间，负荷高峰时段一方面由于火电机组受煤质、设备和供热等因素的影响，调峰幅度不能满足设计调峰要求，影响了电网对风电的接纳；另一方面由于风电自身的随机性和间歇性特征，根据负荷高峰时段时风电累计概率分布(如图 8所示)可知，在 95%的置信度下，风电保证容量在装机容量的 3%以下，此时需要开启足够容量的常规机组来确保系统的安全稳定运行，进一步降低了系统调峰能力和对风电的接纳空间。考虑到风资源条件以及调峰现状，首先需要加快调峰电源建设，配备较大的调峰容量；其次需要将风电纳入日前调度计划和日内的电力电量平衡中，日内进行日前调度计划滚动调整，以满足风电接入对电网调峰要求，解决省级电网调峰与风电消纳之间矛盾。

3.3 A地区风电集中接入对电网的影响

A地区是省级电网风电集中接入地区，为省级电网末端，电网结构薄弱。通过分析A地区集中接入点之一的临近 3个风电场的风电出力(如图8所示)可知，这3个风电场出力表现出很强的相关性，导致风电总出力波动大，对电网冲击大，影响电网稳定性。此外，A地区风电场出力之间相关性强，同时率高，该地区最大负荷仅为900 MW，而风电的装机容量已接近 2000 MW，大量风电必须外送。由于受该地区网架结构限制，风电大发时经常发生输电线路接近满载，在风电外送断面接近稳定极限的情况下，不得不采取弃风的措施，A地区风电消纳问题严重。因此，风电集中接入规模应依据电网实际条件和建设进度进行合理评估，保障风电健康有序发展。

4 结论

本文以分析风电出力时序特性对电网调度运行影响为目的，从出力分布特性、波动性及相关性3个方面分析了风电时序特性，得出以下结论：

1）文中风电场群出力时序特性具有以下特点：风电出力具有明显的季节性，春秋季风电月利用小时数最大，冬季次之，夏季最小；风电出力大波动过程一般持续时间较长，超过24 h，且波动率大，对电网运行影响显著；当风电场之间的距离比较近时，出力相关性高，波动大，随着距离增大，出力平滑性增加，波动减小。

2）在风电装机容量不超过一定比例时，风电波动对系统调频要求低，在短时间尺度下可由机组一、二次调频完成。风电具有明显的反调峰特性，需要加快调峰电源建设，将风电纳入日前、日内调度计划，以满足风电调峰的需求。

3）A地区为省级电网风电集中接入地区，同一接入点的风电场之间出力的相关系数高，风电总出力的波动大，对电网的冲击大，不利用风电的接纳；同时由于大规模风电接入点一般位于电网末端，受网架结构限制，风电输送容量有限，A地区风电消纳问题严重。