改进鲸鱼群算法及其在炼钢连铸调度中的应用
曾 冰, 王梦雨, 高 亮, 董昊臻
(华中科技大学 机械科学与工程学院,湖北 武汉 430074)
0 引言
当前,群体智能优化算法在工程优化问题中的应用日益广泛,特别是针对NP-hard问题,比如车间调度问题[1-2]、WSNs分簇问题[3-4]以及多处理器调度问题[5]等.这些工程优化问题通常是多峰优化问题,即它们的目标函数通常会有多个全局最优解.如果运用逐点式的传统数值优化方法来求解这些问题,需要重复计算多次,再从这些解中选出最优的解,但并不能保证该解是全局最优解[6].群体智能优化算法通过个体之间的合作与竞争来引导种群的迭代,从而向更优的解收敛;并且它们的迭代规则不依赖于函数的导数或梯度等信息,易于使用.因此,越来越多的群体智能优化算法被人们用来解决实际工程优化问题.
受鲸鱼群利用超声波通信进行捕食等行为的启发,华中科技大学的曾冰和高亮于2017年提出了一种新型群体智能优化算法——鲸鱼群算法[7](whale swarm algorithm,WSA),在函数优化问题的求解中取得了显著效果.
1 鲸鱼群算法的原理
鲸鱼群算法是一种基于群体智能的元启发式算法.类似于粒子群算法,鲸鱼群算法首先从定义域内随机生成一组初始解,即随机初始化种群各个体的位置,然后根据种群中各个体的位置和适应度值,以某种机制产生新一代种群.但不同于粒子群算法通过跟踪个体历史最优解和全局最优解生成新种群的机制,鲸鱼群算法模拟鲸鱼群以超声波为信息媒介进行捕食等群体行为,将每个解类比为一条鲸鱼,每条鲸鱼的移动由比它好(由适应度值判断)的鲸鱼中离它最近的鲸鱼引导,笔者将这种引导鲸鱼定义为“较优且最近”的鲸鱼.
2 鲸鱼群算法的基本步骤
在鲸鱼群算法中,每条鲸鱼表示解空间中的一个候选解,解的优劣根据由优化目标定义的适应度函数判断.WSA先对鲸鱼群各个体的位置进行随机初始化,并在之后的迭代过程中,对种群中的每条鲸鱼X,判断其“较优且最近”的鲸鱼Y是否存在,若存在,则鲸鱼X在鲸鱼Y的引导下进行随机移动,如式(1)所示;否则,鲸鱼X的位置保持不变.WSA的基本流程如图1所示.
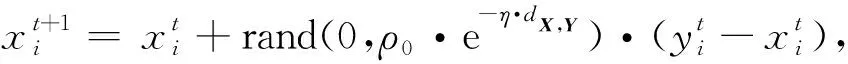
(1)

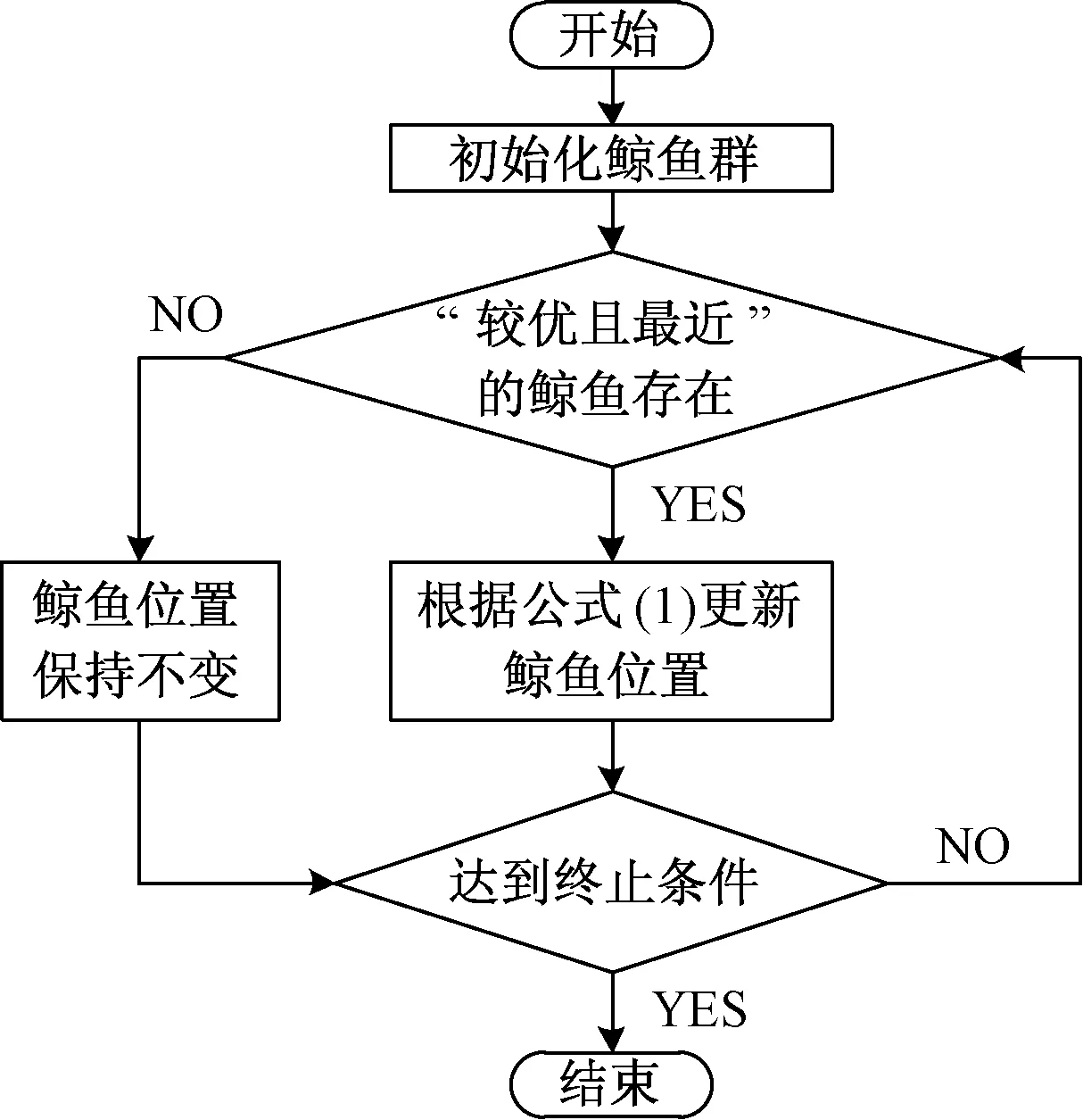
图1 鲸鱼群算法的流程图Fig.1 Flow chart of whale swarm algorithm
根据式(1)可知,如果一条鲸鱼与它的“较优且最近”的鲸鱼之间的距离很小,该条鲸鱼将会积极地朝其“较优且最近”的鲸鱼随机移动;否则,它将消极地朝其“较优且最近”的鲸鱼随机移动,如图2所示.图2中的目标函数维数为2,六角星表示全局最优解,圆圈表示鲸鱼,用虚线标记的矩形区域是当前迭代中鲸鱼的可达区域.
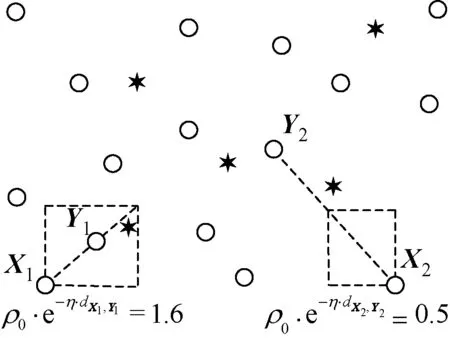
图2 由“较优且最近”的鲸鱼引导的随机移动Fig.2 Random movement under the guidance of the“better and nearest” whale
3 鲸鱼群算法与典型群体智能优化算法的比较
群体智能优化算法主要通过模拟生物的群集行为,利用种群的群体智慧进行协同搜索.这类算法对目标函数的性态(单调性、可导性、模态性等)几乎没有限制,使用简单高效,可广泛地应用于各类优化问题.典型的群体智能优化算法有粒子群优化(particle swarm optimization,PSO)算法、蚁群优化(ant colony optimization,ACO)算法等.
受鸟群觅食行为的启发,PSO采用速度-位置模型,通过动态跟踪个体历史最优解和全局最优解在解空间内进行搜索.PSO主要应用于连续优化问题,所需设置的参数较少,收敛速度较快,但无法直接用于求解离散优化问题.ACO模拟蚂蚁的觅食行为,通过动态更新各路径上的信息素,使蚂蚁在信息素的引导下找到最短路径.相较于PSO,ACO适用于求解离散优化问题(如最短路径问题),但需要调整较多的参数.而WSA主要针对连续优化问题设计,由于其框架易于扩充的特点,可通过简单的改进应用于离散优化问题.将候选解视为鲸鱼,采用向“较优且最近”的鲸鱼随机移动的位置更新模型,在保持种群多样性的同时进行有效的局部搜索,有利于求解多个全局最优解.此外WSA控制参数较少,易于使用.
WSA与近几年提出的头脑风暴优化(brain storm optimization,BSO)算法[8-9]存在诸多相似之处:两者均充分利用种群个体的位置分布信息引导最优解的搜索.其主要区别在于引导方式,WSA主要通过个体向“较优且最近”的鲸鱼移动促使算法收敛至最优解;BSO则基于问题特征和解数据的分析,采用数据挖掘技术引导算法搜索最优解.
4 鲸鱼群算法的改进
4.1 WSA迭代规则的改进
为解决WSA中参数η设置的难题,假设超声波的强度在水中不会衰减,即η=0,则ρ0·e-η·dX,Y=2.当鲸鱼X在“较优且最近”的鲸鱼Y的引导下随机移动时,若X和Y分别位于不同的全局最优解附近,如图3所示,X很可能离开附近最优解所在区域,降低了算法的局部搜索能力.因此,对WSA中鲸鱼的位置更新规则进行如下改进:为当前迭代的鲸鱼(即正本)生成一个副本,若副本在其“较优且最近”的鲸鱼引导下随机移动到优于正本的位置,则正本移至副本所在位置;否则正本保持原地不动.这样图3中的鲸鱼X会以很大的概率保持原地不动,从而引导其他个体向其追随的最优解收敛.可见,改进后的位置更新规则仍然适用于η=0的情况,可以在不引入任何小生境参数的前提下,有效保证多个子种群的形成,提高算法的局部搜索能力,这非常有利于求解多个全局最优解.
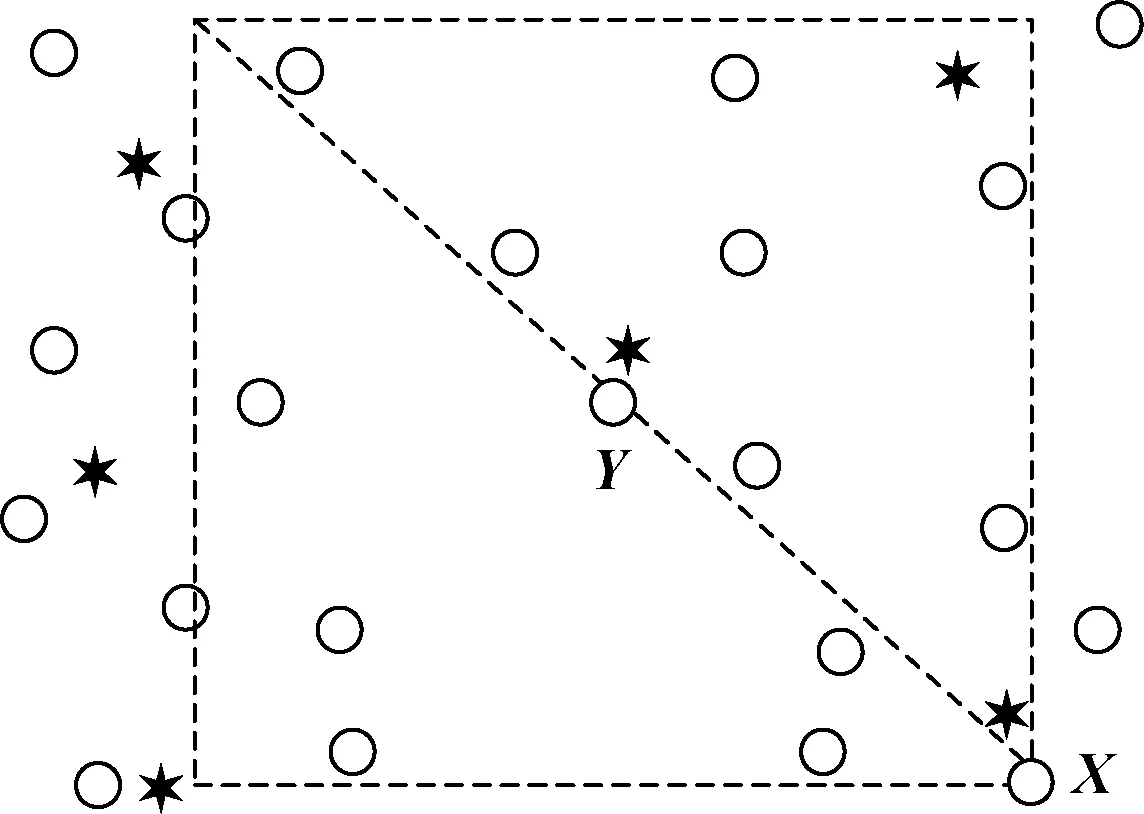
图3 当η=0时,由“较优且最近”的鲸鱼引导的随机移动Fig.3 Random movement under the guidance of the“better and nearest” whale when η=0
4.2 在迭代过程中识别并跳出已找到的极值点
为使WSA在迭代过程中有效识别并跳出已找到的极值点,提高算法的全局搜索能力,引入稳定性阈值Ts和适应度阈值Tf两个参数.稳定性阈值Ts是一个预先定义的迭代次数,用来判断一条鲸鱼是否已经找到所跟随的极值点,达到稳定状态.为实现上述判断,每条鲸鱼设置一个迭代计数器c,以记录该鲸鱼未更新位置的迭代次数.适应度阈值Tf用于识别当前全局最优解.在每次迭代过程中,对于种群中未更新的鲸鱼X,需检查其迭代计数器:若X未达到稳定状态(即X.c≠Ts),则其迭代计数器自增1;反之,根据Tf和|fgbest-f(X)|的大小(fgbest为当前全局最优适应度;f(X)为X的适应度),判断是否更新当前全局最优解集合,接着初始化该鲸鱼,从而跳出已经找到的极值点.基于上述对WSA的改进方案,改进的WSA被称为带迭代计数器的WSA(WSA with iterative counter,WSA-IC).
4.3 WSA-IC算法的流程
初始化鲸鱼包括初始化鲸鱼的位置以及将鲸鱼的迭代计数器置0.
WSA-IC算法伪代码如下.
输入: 目标函数,鲸鱼群Ω.
输出: 当前全局最优解集GloOpt.
1:开始
2:初始化参数;
3:初始化鲸鱼;
4:计算鲸鱼的适应度值;
5:while 终止条件不满足 do
6:fori=1 to |Ω| do
7:寻找Ωi的“较优且最近”的鲸鱼Y;
8:ifY存在 then
9:生成Ωi的副本X′;
10:X′在Y的引导下根据公式(1)移动;
11:计算X′的适应度值f(X′);
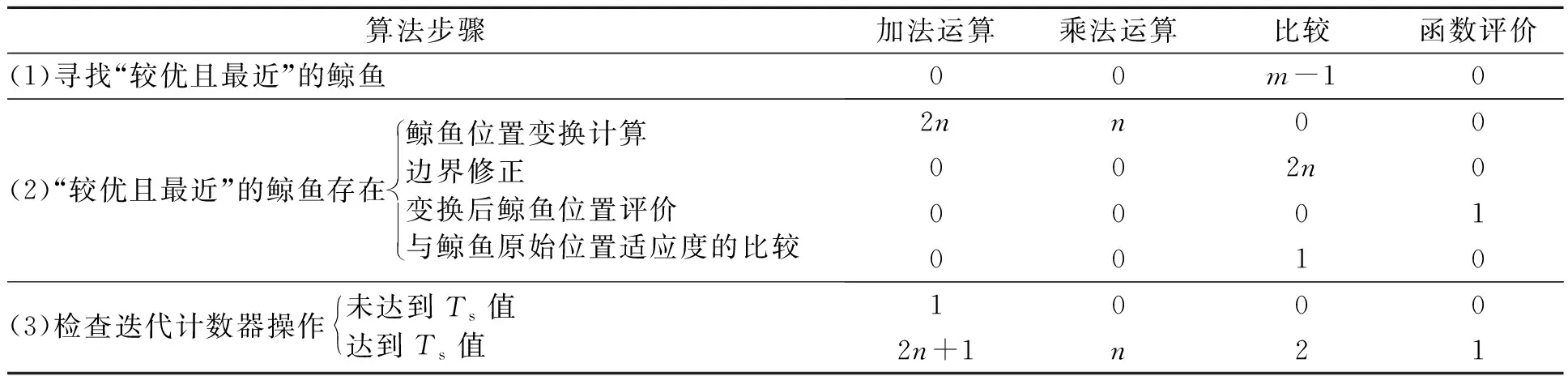
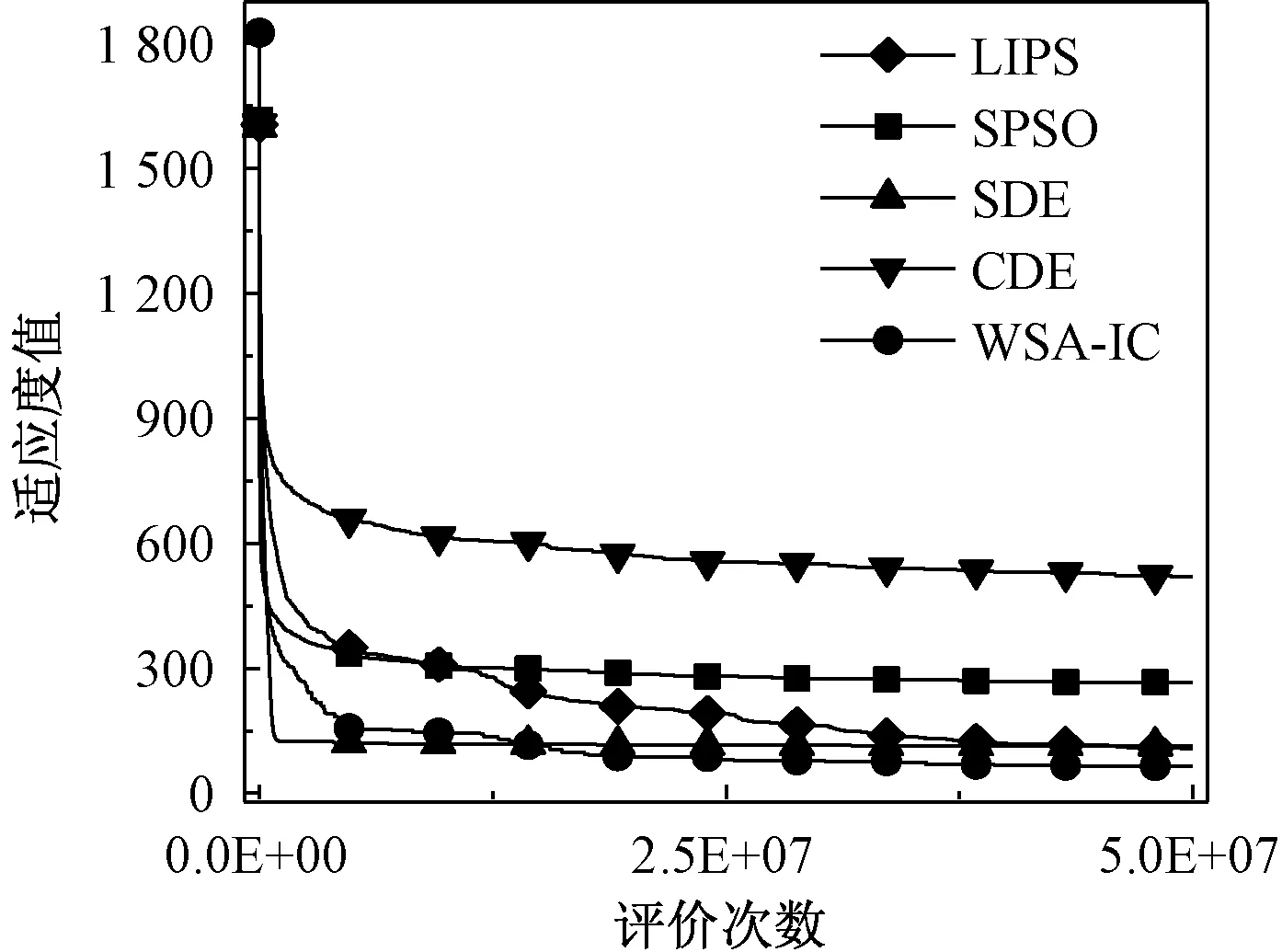
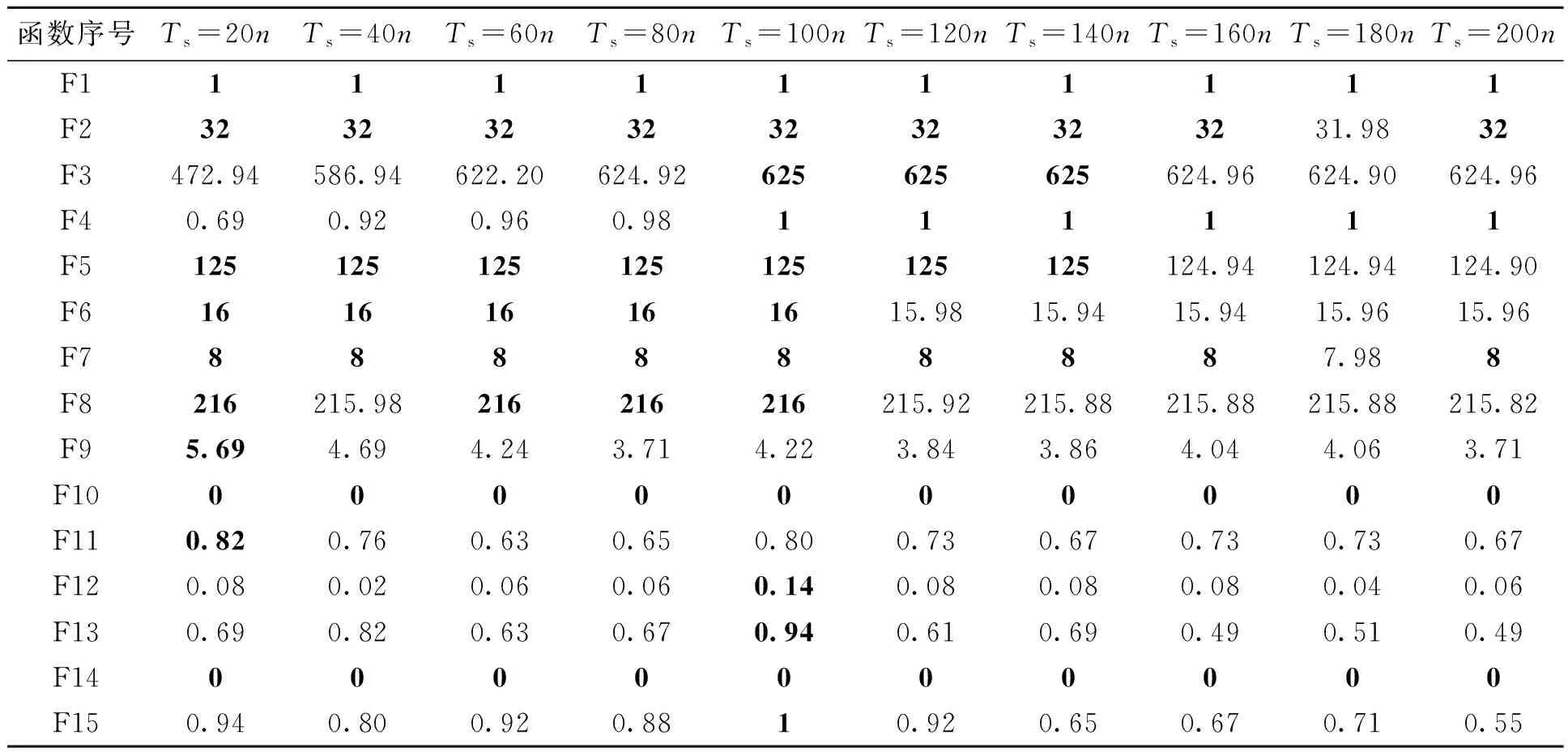
12:iff(X′) 13:Ωi=X′; 14:Ωi.c=0; 15: else 16:检查Ωi的迭代计数器; 17:end if 18:else 19:检查Ωi的迭代计数器; 20:end if 21:end for 22:end while 23:判断Ω中的每条鲸鱼是否是当前全局最优解; 24:返回GloOpt; 25:结束 4.4.1 复杂度分析 WSA-IC算法的时间复杂度分析见表1,种群规模和目标函数维度分别为m、n.在复杂度最高情况下,即当鲸鱼在位置变换时没有发现适应度更优的个体且迭代计数器达到阈值Ts,更新鲸鱼个体需执行4n+1次加法、2n次乘法和2n+m+2次比较.因此,WSA-IC算法的时间复杂度为O(n2). 4.4.2 收敛性分析 由式(1)及WSA-IC算法伪代码可知,WSA-IC算法可写成如下形式: (2) 式中:A=1-rand(0, 2),B=rand(0, 2). 因此可通过计算求得E(A)=0,E(B)=1,D(A)=D(B)=-E(AB)=1/3. 表1 WSA-IC算法复杂度分析Tab.1 Analysis of the algorithm complexity for WSA-IC (3) (4) (5) (6) (7) 由式(5)、(7)推出 (8) (9) WSA-IC算法包含4个参数,即超声波源强度ρ0、衰减系数η、稳定性阈值Ts以及适应度阈值Tf.其中,ρ0和η分别被设置为2和0;Tf通常认为与给定的适应度误差(即精度)相等,当精度未给定时,可设置为1.0×10-8;基于大量实验结果,Ts的值一般设置为函数维度的100倍. 采用如下6个多峰优化算法作为对比算法:locally informed PSO(LIPS)[6]、fitness-euclidean distance ratio PSO(FERPSO)[10]、speciation-based DE(SDE)[11]、crowding DE(CDE)[12]、speciation-based PSO(SPSO)[13]以及WSA.所有算法都是在Microsoft Visual Studio 2015中用C++编程语言实现,在相同的环境下运行,停止条件均为CPU计算时间. 4.6.1 测试函数 测试函数采用15个CEC2015多峰基准测试函数,其基本信息如表2所示.表中n、o1、o2分别表示函数维度、全局最优解个数、局部最优解个数.所有的测试函数都是最小化问题,其搜索空间均为[-100, 100]n. 表2 CEC2015多峰测试函数Tab.2 CEC2015 multimodal functions for the experiment 4.6.2 参数设置 算法的主要参数设置如表3、表4所示.在表3中,m1/m2表示WSA-IC算法的种群大小/其他算法的种群大小,CPU计算时间以s为单位.由于WSA-IC算法在迭代过程中可以有效识别并跳出已经找到的极值点,因此可以设置相对较小的种群规模,以降低算法的计算复杂度. 表3 CEC2015多峰测试函数相关参数的设置Tab.3 Setting of parameters associated with CEC2015 multimodal functions for the experiment 表4 7种算法主要参数的设置Tab.4 Setting of main parameters of seven algorithms 注:ω为惯性权重;nsize为邻居个数;χ为收缩因子;φmax为系数;CR为交叉概率;F为缩减因子;n为种群大小;CF为拥挤因子;φ1、φ2为系数. 4.6.3 评价指标 为保证比较的公正性,每个算法在每个测试函数上独立运行51次,并从最优解数量、最优解质量、收敛速度三方面来度量算法的性能. 4.6.4 实验结果与分析 (1)最优解的数量.算法在最优解数量方面的表现通过平均最优解个数(average number of optima found,ANOF)衡量.算法的ANOF值及显著性水平为0.05时的Z检验结果见表5.表中,avg±sd表示算法取得的ANOF均值±标准差;δ表示Z检验结果,且符号“+”(“-”)表示WSA-IC算法的结果优于(劣于)对比算法且差异显著,符号“=”表示WSA-IC算法和对比算法结果的差异不显著.总体看来,符号“-”的数量只有1个,针对每种对比算法,符号“+”的数量占多数,意味着WSA-IC算法在最优解数量上的表现远好于其他算法. 表5 7种算法在测试函数上获得的ANOF值与Z检验结果Tab.5 ANOF of seven algorithms on test functions and results of Z-test (2)最优解的质量.将算法取得的最优解适应度值减去100与相应函数序号的乘积,由此得到的最优解均值(标准差)及Z检验结果如表6所示,分别用avg(sd)和δ表示.显然,符号“-”的数量远少于符号“+”和“=”的数量,说明WSA-IC算法取得了较高的最优解精度. (3)收敛速度.在比较算法的求解效率时,以算法在测试函数F14上的收敛曲线为例进行分析,如图4所示.横坐标为评价次数,纵坐标为算法多次实验找到的当前全局最优解适应度均值.由于FERPSO和WSA的种群可能会过早收敛而停止迭代,对比算法不包括这两个算法.从图4可以看出,相比于其他算法,WSA-IC算法在F14上以更快的速度收敛到更优的解. 综上所述,WSA-IC算法能高效地搜索到更多更优的解,这主要得益于对WSA两方面的改进:其一,改进迭代规则,使WSA-IC算法在保证多个子种群形成的同时保持局部搜索能力;其二,在迭代过程中识别并跳出已经找到的极值点,加速WSA-IC算法向全局最优解收敛,尽可能地提高算法的全局搜索能力. 表6 7种算法在测试函数上获得的最优解质量与Z检验结果Tab.6 Quality of optima found by seven algorithms on test functions and results of Z-test 图4 算法在函数F14上的收敛情况Fig.4 Convergence rate of algorithms on F14 (4)参数的影响.稳定性阈值Ts是WSA-IC算法最为关键的参数,其值需根据优化问题的特点设定.对取不同Ts值的WSA-IC算法进行了实验,结果如表7所示.由表7可知,当Ts=100n时,WSA-IC算法在大部分测试函数上都能取得最优的ANOF值.因此,对于几乎所有的连续优化问题,Ts均可以设置为100n. 目前鲸鱼群算法已在某些工程优化领域(如无线传感器网络能效优化)获得了成功的应用.下面以炼钢连铸调度问题为例介绍鲸鱼群算法的具体应用. 以某钢厂的工艺流程为例介绍炼钢连铸调度问题.如图5所示,有N个待加工浇次,各浇次包括一定数目的炉次,需按同一工艺路线(EAF-AOD-LF1-LF2-CC)进行加工,要求在保证连铸阶段相邻浇次预留准备时间,同一浇次内炉次连续加工的前提下,确定浇次顺序、连铸机分配和各工序的开始时间及结束时间,以最小化最大完工时间.此外,特定工序间设置一定数量的无限缓冲区、有限缓冲区和可加工缓冲区[14].其中,无限缓冲区不限制炉次的缓存时间;有限缓冲区中炉次的缓存时间受限;可加工缓冲区既可加工炉次又可缓存炉次且缓存时间不受限.这类问题早已获得某些学者的关注[14-15],但不同于已有的研究,笔者考虑连铸阶段存在2台并行机的情况,将缓冲区视为加工时间为0的生产阶段,则笔者所研究的炼钢连铸调度问题实质上是9阶段零等待混合流水车间调度问题. 表7 WSA-IC算法在不同的Ts取值下获得的ANOF值Tab.7 ANOF of WSA-IC with different values of Ts 图5 钢铁生产工艺流程图Fig.5 Flow chart of the steel production process 由于调度问题的离散特性,WSA-IC算法不能直接用于求解炼钢连铸调度问题,因此从如下4个方面对WSA-IC算法进行了改进:①设计了一种离散的鲸鱼个体编码与解码方案;②采用汉明距离计算个体间的距离;③改进了鲸鱼个体的移动规则;④设计了一种有效的自适应邻域搜索策略.由于该算法不需要保存在迭代过程中求得的多个当前全局最优解,所以该算法不需要Tf参数. 基于WSA-IC的炼钢连铸调度算法伪代码如下. 输入:目标函数,鲸鱼群Ω,当前全局最优解GBest,当前全局最优解的适应度值fgbest. 输出:最优解. 1:开始 2:初始化参数; 3:初始化鲸鱼; 4:计算鲸鱼的适应度值; 5:while 终止条件不满足 do 6:fori=1 to |Ω| do 7:寻找Ωi的“较优且最近”的鲸鱼Y; 8:ifY存在 then 9:生成Ωi的副本X′; 10:X′根据个体移动规则向Y移动; 11:计算X′的适应度值f(X′); 12:iff(X′) 13:Ωi=X′; 14:Ωi.c=0; 15:else 16:ifΩi.c≠Tsthen 17:Ωi.c=Ωi.c+1; 18:else 19:重新初始化Ωi; 20:计算Ωi的适应度值; 21:end if 22:end if 23:else 24:生成的Ωi副本X′; 25:对X′执行自适应邻域搜索; 26:iff(X′) 27:Ωi=X′; 28:Ωi.c=0; 29:else 30:ifΩi.c≠Tsthen 31:Ωi.c=Ωi.c+1; 32:else 33:iff(Ωi) 34:fgbest=f(Ωi); 35:GBest=Ωi; 36:end if 37:重新初始化Ωi; 38:计算Ωi的适应度值; 39:end if 40: end if 41:end if 42:end for 43:end while 44:判断最后一代种群中是否有比GBest好的鲸鱼,有则替换GBest; 45:返回最优解GBest; 46:结束 5.2.1 个体编码与解码 算法基于工件进行编码,即将浇次编号的排序作为编码.解码采用文献[14]所提方法,根据编码所示浇次序列,以浇次为单位安排作业计划,其中连铸机的分配依据最早空闲机器优先规则. 5.2.2 个体间的距离计算 在上述离散个体编码方案中,个体维度都相同,个体之间的距离计算与等长字符串之间的距离计算非常相似,故采用汉明距离[16]计算不同鲸鱼个体间的距离.假设两条鲸鱼个体X1、X2如图6所示,X1和X2有4个元素不相同,所以,X1和X2之间的汉明距离为4. 图6 两条鲸鱼个体示意图 5.2.3 个体移动规则 由于个体采用离散编码方案,WSA算法的个体位置迭代式(1)不再适用,因此需针对炼钢连铸调度问题,改进个体移动规则.为了保证当前个体向它的“较优且最近”的个体随机移动,引入一个新的参数——选择概率λ.鲸鱼Ωu的副本X′在它的“较优且最近”的鲸鱼Y的引导下,进行如下移动:首先比较个体X′和Y中对应位置的元素,如果不同,则将该元素的值和位置分别存入集合A和B中;遍历这些不同元素所在的位置,生成一个0到1之间的随机数P,若P小于λ且Y中该位置的元素属于集合A(存储未被选择的元素),则将Y中该元素赋值给X′中对应位置的元素,否则从集合A中随机选择一个值赋给X′中对应位置的元素.注意到已经赋值给X′的元素应从集合A中移除. 5.2.4 自适应邻域搜索策略 为增强算法的局部搜索能力,当种群中不存在当前鲸鱼个体的“较优且最近”的鲸鱼时,对当前个体进行结合移位算子和交换算子的自适应邻域搜索.自适应邻域搜索方法将种群不同个体与生成该个体的邻域搜索算子关联起来.首先比较区间[0,1]内的随机数a和自适应邻域搜索概率ϑ的大小,若a<ϑ,选择关联的邻域算子进行局部搜索;反之,则从交换算子和移位算子中任选一种邻域算子实现局部搜索. 为验证本文算法的有效性,随机生成5个不同规模的案例,选择遗传算法(genetic algorithm,GA)、人工蜂群算法(artificial bee colony,ABC)、传统WSA算法作为比较算法.WSA-IC算法的参数设置如下:种群规模PS为50,选择概率λ为0.5,自适应邻域搜索概率ϑ为0.75,稳定性阈值Ts为200+|Z|/2(|Z|为浇次数).所有算法以相同的迭代次数为终止条件,每组实验运行10次,结果见表8.由表8知,对于测试的5个案例,WSA-IC算法均能找到优于ABC、GA和WSA算法求得的解,并取得较小的标准差,且这种差异随着案例规模的增大而增大.由此说明,笔者提出的算法具有良好的寻优能力和稳定性.图7为所示算法的收敛曲线(横坐标为迭代次数,纵坐标为每次迭代求得的最优解适应度值).从图7可知,相较于GA、ABC和WSA算法,WSA-IC算法能更快地收敛到更优的解. 图7 算法调度90个浇次时的收敛情况Fig.7 Convergence rate of algorithms for the case of scheduling 90 casts 表8 WSA-IC算法与其他算法的实验结果Tab.8 Experimental results of WSA-IC and other algorithms 研究了一种新兴的群体智能算法——鲸鱼群算法(WSA).针对多峰函数优化问题的特点,提出了改进的鲸鱼群算法(WSA-IC).WSA-IC改进了WSA的迭代规则,并引入了“稳定性阈值”和“适应度阈值”两个参数,使算法能在迭代过程中有效地识别并跳出已找到的极值点.结果表明,WSA-IC在求解多峰函数优化问题上有着优异的性能,且WSA-IC的参数极易设置.此外,以炼钢连铸调度问题为例,阐述了WSA在工程优化领域的具体应用,表明WSA具有较大的应用价值. 当前关于WSA的研究仍处于起步阶段,未来可以将WSA与其他元启发式算法相结合以提高算法的优化性能;本文实验已证明WSA对多峰连续优化问题以及炼钢连铸调度问题的适用性,未来可以研究WSA在其他实际工程优化问题(特别是NP-hard问题)中的应用.4.4 WSA-IC算法复杂度及收敛性分析
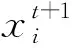
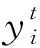
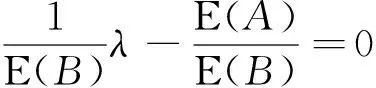

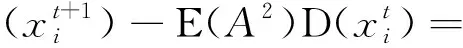

4.5 WSA-IC算法的参数设置
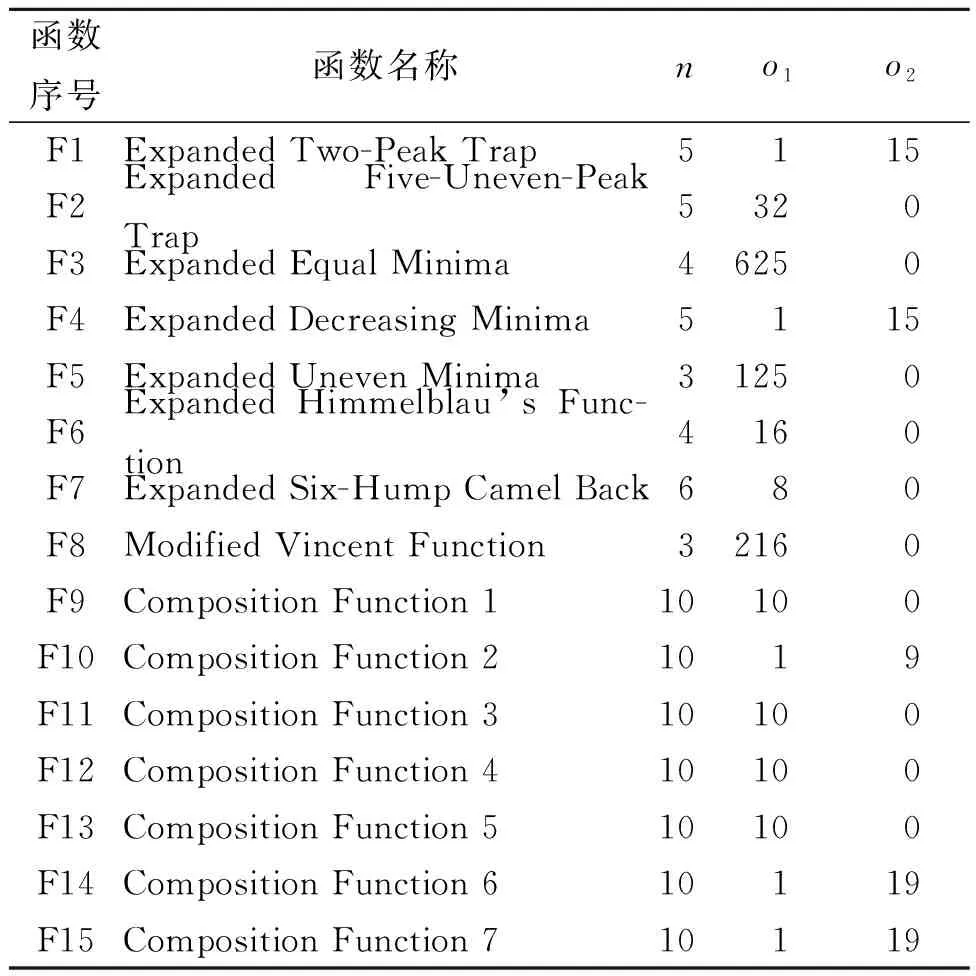
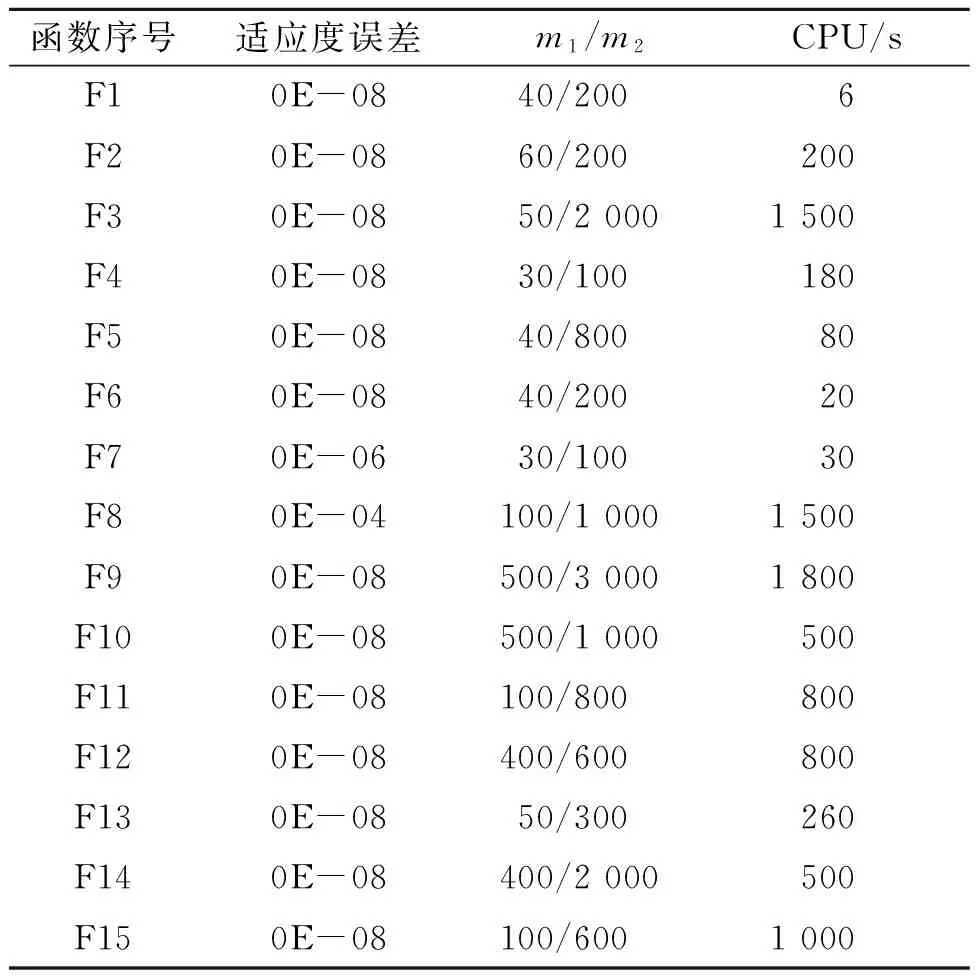
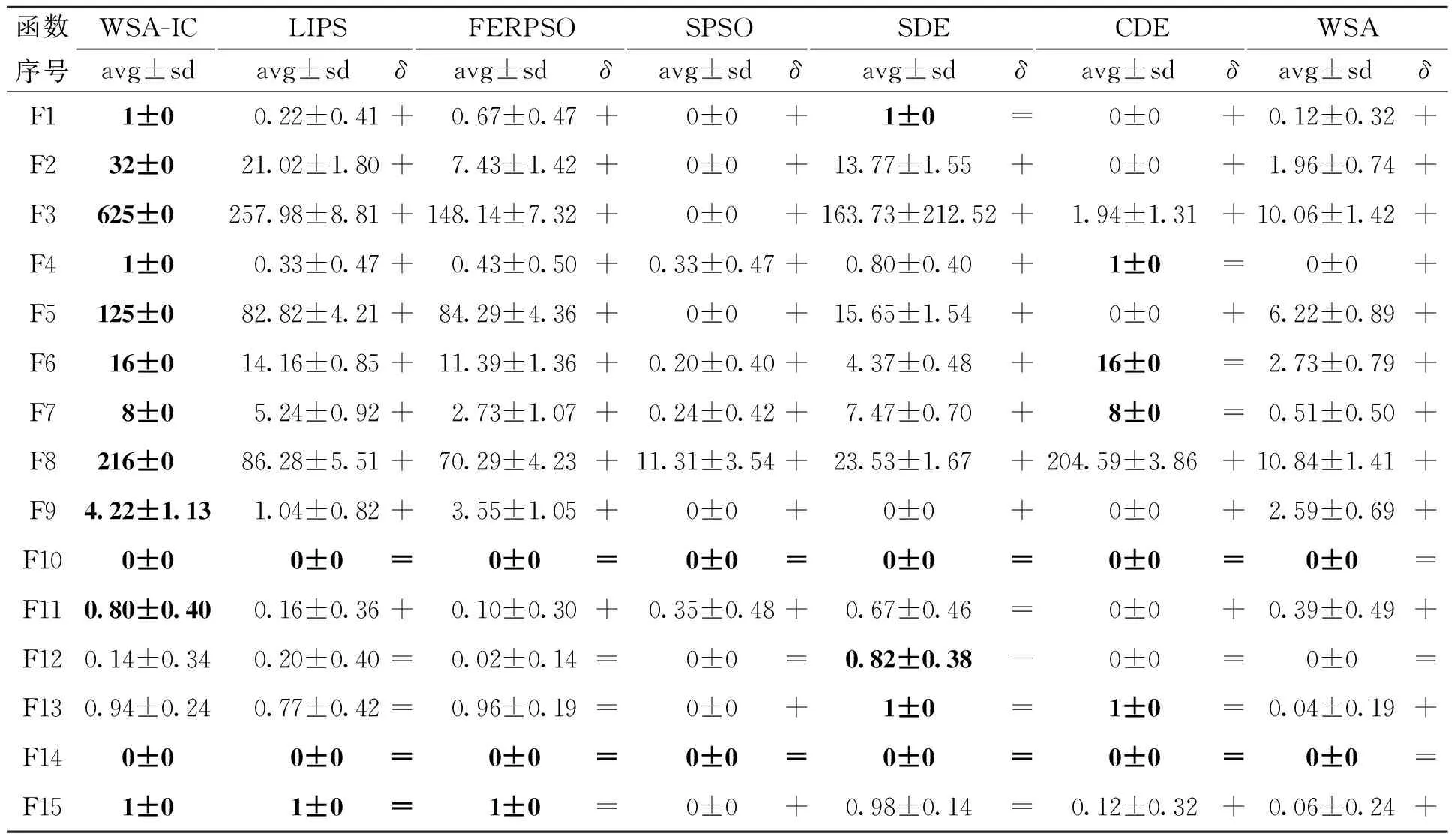
4.6 数值实验


5 鲸鱼群算法的应用
5.1 炼钢连铸调度问题
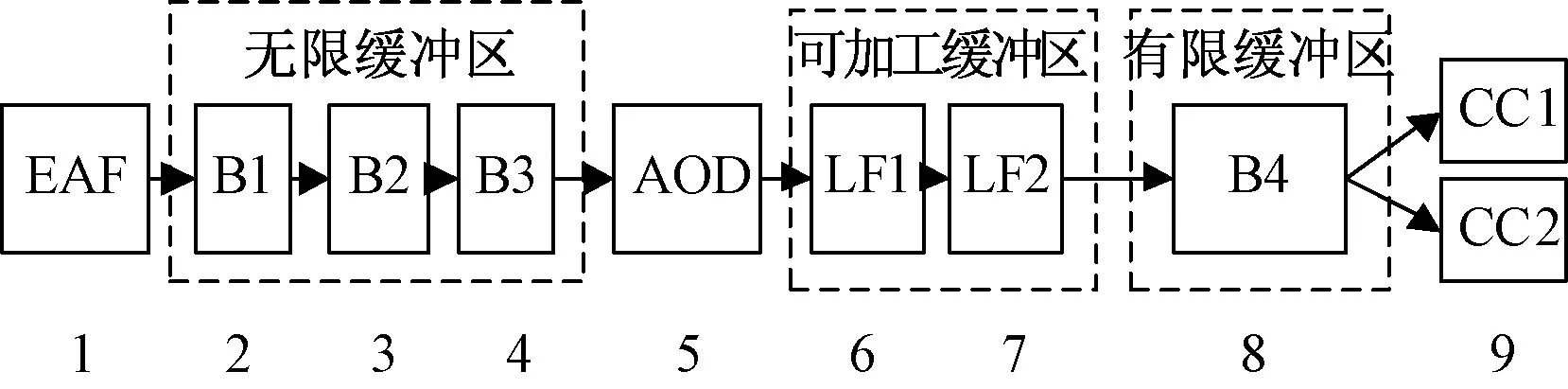
5.2 基于WSA-IC的炼钢连铸调度算法
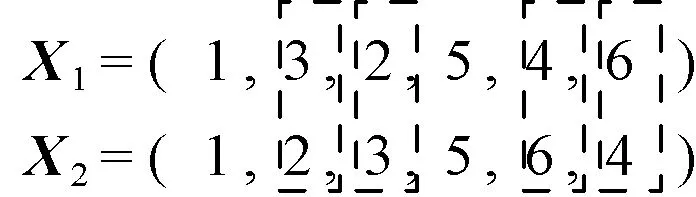
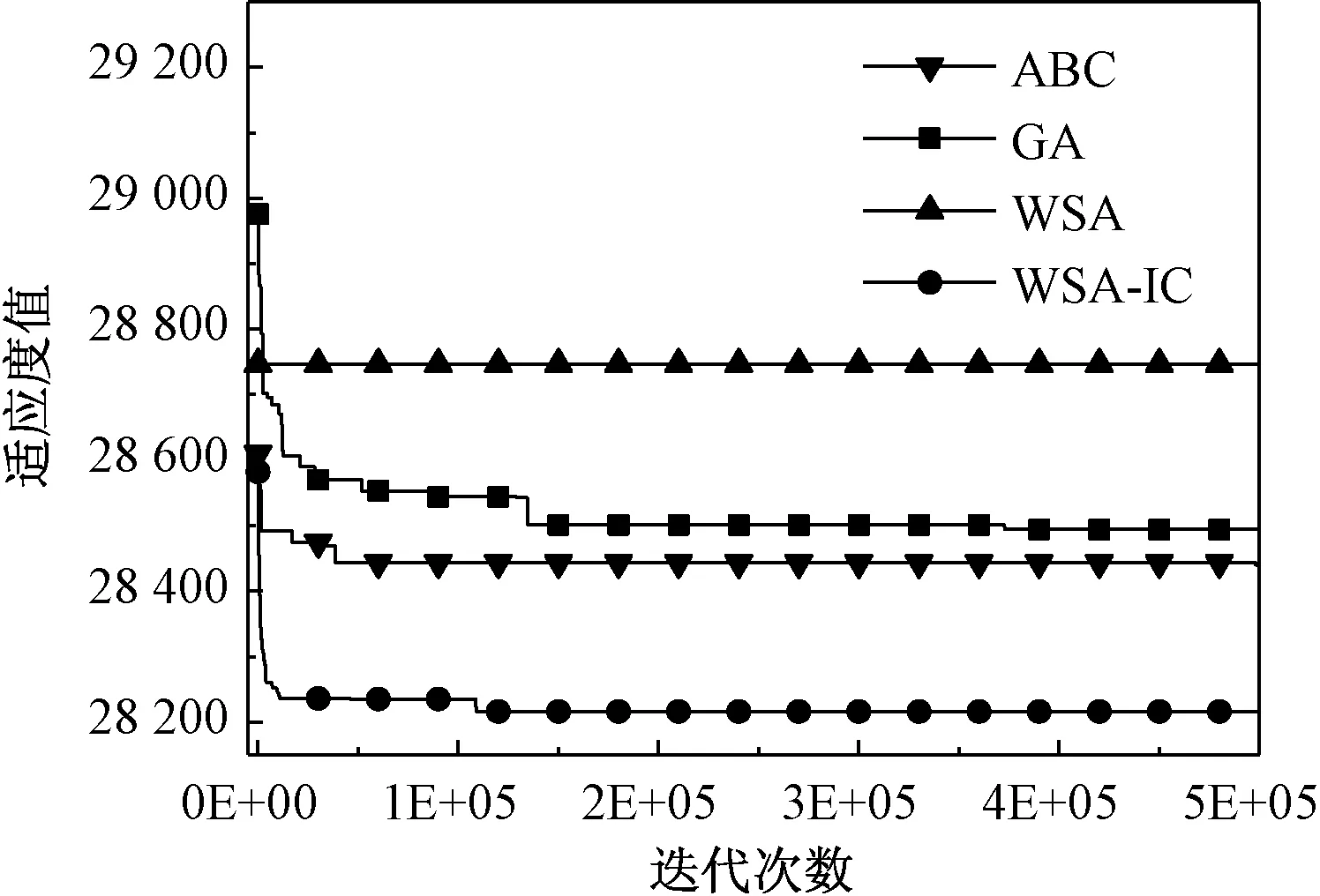
Fig.6 Sketch map of two whales5.3 实例仿真与分析

6 结束语

