基于鸽群优化算法的含分布式电源配电网状态估计

白 晨,姚李孝,曹 雯

(1.西安理工大学水利水电学院,陕西西安 710048;2.西安工程大学电子信息学院,陕西西安 710048)

全球经济发展,导致对能源的需求量不断加大,传统能源短缺以及环境污染问题日趋突出,加快了风能和太阳能等清洁能源的发展。这些清洁能源以分布式发电(Distributed Generation,DG)的形式并入配电网,就地消纳,随着DG的渗透率不断提高,配电网运行方式越来越复杂,对配电网的运行管理模式提出了更高的要求。

为保证DG大规模安全并网运行,采取了很多措施[1-4],如制定DG并网标准[1],选取DG接入位置、确定DG注入容量[2-3],评估DG并入电网的可靠性[4-5],DG并入电网的优化控制[6-7]等。然而,在采取这些措施之前,利用量测装置获得的量测数据会有一定误差,DG并入电网增加了其结构的复杂性,这些因素对电网的控制与运行都会造成不利影响。状态估计[8]是提高量测精度的有效方法,其目的是根据获取的配电网的各种量测信息,估计配电网系统当前的运行状态,国内外学者在研究含DG配电网状态估计方面取得了一些进展,可以归纳为三个方面:第一个方面是从对含DG配电网建模的角度出发,通过简化风力发电机等效模型[9],将滑差值引入状态估计过程,建立了计算精度较高的数学模型;卫志农等[10]提出了DG并网三相模型,它是将外网边界状态量估计值作为本区域伪量测值的分布式状态估计方法。第二个方面是考虑到量测值中存在不良数据,基于PMU的不良数据检测与辨识[11],提出了一种分析电力系统可观测性的混合拓扑/数值方法;针对电网中注入不良数据和恶意攻击数据[12],提出基于信息技术的电网的自愈能力模式的状态估计方法。第三个方面是基于智能优化算法的含DG配电网状态估计计算方法,如采用自适应免疫粒子群算法进行配电网状态估计[13],该算法可提高全局搜索能力,而且收敛速度和精度较为理想;针对建立的含DG配电网的状态估计模型,提出一种求解状态估计模型的变异粒子群优化-禁忌搜索混合算法[14],能够取得精度较高的状态估计结果。

鸽群优化算法[15](Pigeon-Inspired Optimization Algorithm,PIOA)是近年来提出的一种新兴群体智能优化算法,这一算法是受到自主归巢行为的仿生学原理启发而提出的,模拟鸽群依据磁场、太阳和地标完成归巢的导航过程,通过鸽群反复迭代搜索计算,在解空间获取优化问题的最优解。这一算法原理简单,易于操作,便于编程,自2014年提出以来[16],越来越受到关注,同时也日趋完善[17-19],并在诸多领域的工程优化问题中得到了应用[20-22]。

本文采用鸽群优化算法求解含分布式电源配电网状态估计优化模型,并结合算例验证这一方法的可行性,为这类配电网状态估计提供了一种新的解决途径。

1 状态估计数学模型

1.1 目标函数

以量测值与估计值差值平方和最小为目标,状态变量为负荷节点和与DG节点的有功功率,则含DG配电网的状态估计目标函数为:

(1)

X=[PG,PL](1×n)

(2)

PG=[PG1,PG2,…,PGs](1×s)

(3)

PL=[PL1,PL2,…,PLl](1×l)

(4)

n=s+l

(5)

式中,X为状态变量,由DG的有功功率PG和负荷的有功功率PL组成;r为量测节点序号;R为量测节点总数;zr表示第r个节点的量测值;wr表示第r个节点的权重因子;hr(X)表示第r个节点的量测方程;s表示DG节点的数量;l表示负荷节点的数量;n为配电网节点总数,为s和l之和。

1.2 约束条件

1.2.1 等式约束

含DG的配电网状态估计目标函数的等式约束条件为配电网的潮流约束方程,以节点功率方程的形式表示为:

(i=1,2,…,n，j=1,2,…,n)

(6)

(7)

式中,i为节点序号(包括电源节点和负荷节点);Pi为节点i的有功功率;Qi为节点i无功功率;Ui为节点i电压幅值;Uj为节点j电压幅值;δij为节点i相角δi与节点j相角δj的差值;Gij为导纳矩阵中元素Yij的实部;Bij为导纳矩阵中元素Yij的虚部。

以上等式约束条件式(6)和式(7)可表示为:

gk(X)=0 (k=1,2,…,K)

(8)

式中,k为等式约束条件序号;K为等式约束条件总数,K=2n。

1.2.2 不等式约束

配电网状态估计的不等式约束为状态变量上下限约束:

PGimin≤PGi≤PGimax

(9)

PLimin≤PLi≤PLimax

(10)

式中,PGi为分布式电源节点i的有功功率,PGimax和PGimin分别表示该DG节点i的有功功率上、下限;PLi为负荷节点i的有功功率,PLimax和PLimin分别表示该负荷节点i的有功功率上、下限。

以上不等式约束条件式(9)和式(10)可表示为:

fm(X)≤0 (m=1,2,…,M)

(11)

式中,m为不等式约束条件序号;M为不等式约束条件总数,M=2n。

1.3 量测系统

由于在配电网中量测装置有限,除了量测点得到的实时量测数据以外,为提高状态估计精度,在其他节点和支路设置伪量测值,其主要来源是历史数据。图1为含DG配电网的量测系统。在该系统中,|U|为电压幅值,|I|为电流幅值。量测值包括节点电压幅值量测、支路电流量测、支路功率量测等。

图1 含DG配电网量测系统Fig.1 Measurement system of distribution network with DG

2 求解优化模型的鸽群优化算法

鸽群优化算法就是模拟鸽群依据磁场、太阳和地标完成归巢的导航过程,在求解优化模型过程中通过满足约束条件,在解空间中寻求最优解。这一寻优过程可分为两个阶段,即磁场算子阶段和地标算子阶段,在磁场算子阶段,鸽群远离目的地,主要是依据磁场和太阳的高度导航;当鸽群离目的地较近,可以观测到地物时,进入地标算子阶段。

采用鸽群优化算法,即以鸽子个体(一组状态变量)为一个满足约束条件的可行解,求解上述配电网状态估计优化模型,其流程为:

步骤1 采用罚函数法[23],即在目标函数中引入惩罚项,将有约束条件的配电网状态估计优化问题,变为一个无约束条件优化问题,然后可采用填充函数法求解[24]。由约束条件式(8)和式(11),结合目标函数式(1),定义目标函数为:

minψ(X,z)=J(X)+

(12)

式中,z为罚因子,取很大的正数。

函数G[gk(X)]满足以下条件:

G[gk(X)]=0 当gk(X)=0

(13)

G[gk(X)]>0 当gk(X)≠0

(14)

函数F[fm(X)]满足以下条件:

F[(fm(X)]=0 当fm(X)≤0

(15)

F[(fm(X)]>0 当fm(X)>0

(16)

步骤2 确定种群规模和迭代步数,迭代步数包括磁场算子阶段迭代步数和地标算子阶段迭代步数。

步骤3 初始化,随机生成每个鸽子个体初始位置。

步骤4 磁场算子阶段,在该算法的初始化阶段,根据磁场和太阳的位置,确定飞行的位置和方向,在这个模型中,每个鸽子根据当前迭代中最近的全局最优解来更新它的位置。假设鸽群中第h只鸽子的位置和速度分别为Xh(t)和Vh(t),则有:

Vh(t)=Vh(t-1)e-Wt+rand·(Xp-Xh(t-1))

(17)

Xh(t)=Xh(t-1)+Vh(t)

(18)

式中,W为磁场算子；rand为0～1随机数；Xp为全局最优位置;t为迭代次数。

通过反复迭代,鸽群离目的地越来越近,达到磁场算子阶段迭代步数,转到步骤5。

步骤5 经过磁场算子阶段,鸽群中一些鸽子可能已经找到了目的地或者熟悉的地标,因此,这些鸽子可以快速移动到目的地,其他的鸽子则跟随他们移动,进入地标算子阶段。假设Xc(t)是鸽群的中心位置,它的适应度为Np/2,在每次的迭代循环中,地标算子会将当前个体的适应度进行排序,将适应度低的个体舍弃,把余下鸽子的中心位置当成地标作为飞行的参考方向。其表达式为:

(19)

(20)

Xh(t)=Xh(t-1)+rand·(Xc(t)-Xh(t-1))

(21)

式中,Np为每次迭代过程中一半鸽子的数量,即每次迭代过程将鸽群数量减半;fitness(Xh(t))为第h只鸽子的适应度函数。

据此,反复迭代计算,到达地标算子阶段迭代步数时,转入步骤6。

步骤6 输出最终解。

依据以上步骤,编制MATLAB程序进行计算,获取优化问题的最优解。

3 算 例

为了验证算法,本文以IEEE33配电系统为算例进行状态估计计算。改进后的IEEE33配电系统接线如图2所示,计算时基准功率为100 MVA,基准电压为12.66 kV,在节点3、8、14、20、23、28接入DG。DG平均有功功率和负荷有功功率实测值分别如表1和表2所示。

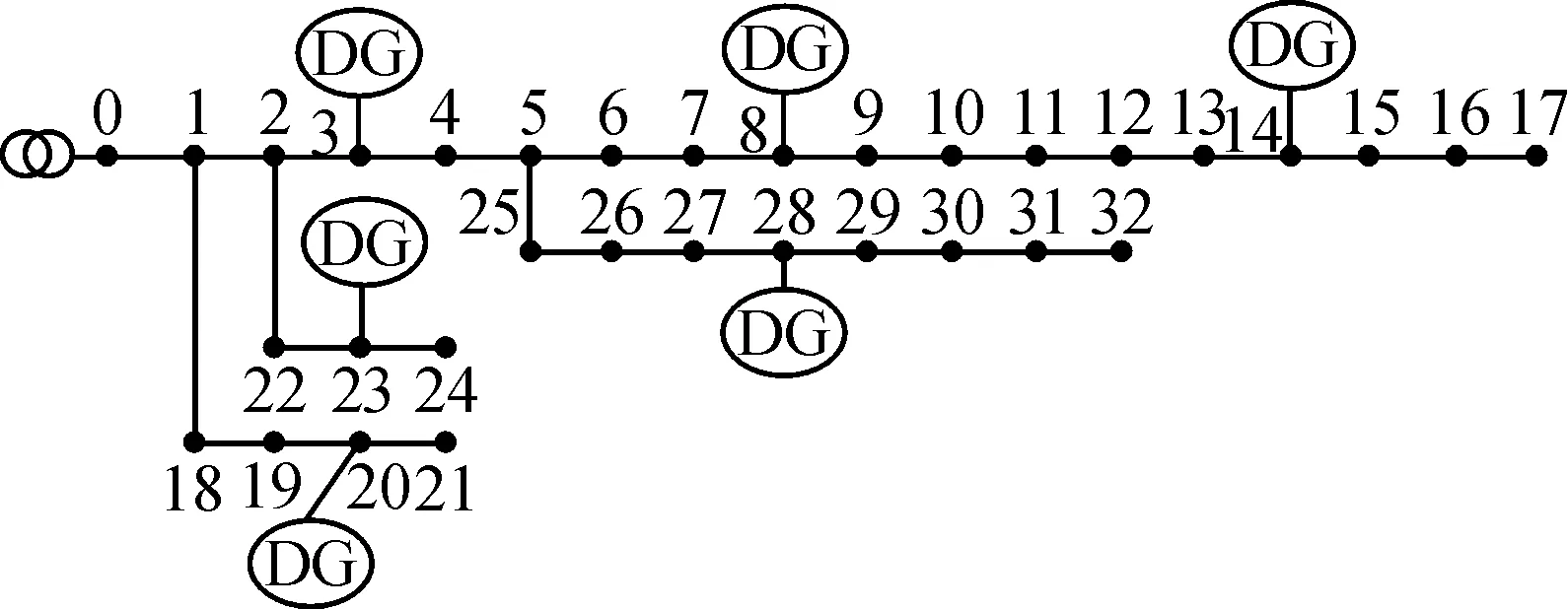
图2 IEEE33配电网示意图Fig.2 Distribution network of IEEE33

设定鸽群规模数为128,总迭代步数为200代,其中磁场算子阶段迭代步数为192代,地标算子阶段迭代步数为8代。将这些参数代入配电网状态估计优化模型,依据本文提出的求解步骤,分别计算与节点相连的DG有功功率估计值和负荷有功功率估计值,见表1和表2中的PIOA估计值。为了验证本文算法的有效性,同时采用遗传算法(GA)分别计算与节点相连的DG有功功率估计值和负荷有功功率估计值,见表1和表2的中GA估计值。

表1 DG有功功率Tab.1 DG active power

表2 负荷有功功率Tab.2 Load active power

为了更加直观地分析鸽群优化算法的误差处理能力,引入均方根误差RMSE(Root Mean Square Error)和平均绝对误差MAE(Mean Absolute Error):

(22)

(23)

式中,v为估计值或者量测值的数量;XE为估计值;XA为量测值;p为组数。

表3为DG有功功率和负荷有功功率的RMSE和MAE在鸽群算法(PIOA)和遗传算法(GA)中的对比。

表3 DG有功功率和负荷有功功率的RMSE和MAE在GA和PIOA中的对比Tab.3 Comparison RMSE and MAE of DG active power and load active power in GA and PIOA

从表3可以看出,在DG的有功功率估计值计算中,PIOA算法中的RMSE和MAE均小于GA算法中的RMSE和MAE;同样,从表3可以看出,负荷的有功功率在PIOA算法中的RMSE和MAE均小于遗传算法中的RMSE和MAE。因此,从DG和负荷有功功率的RMSE和MAE来分析,得到PIOA算法计算状态估计值误差小于GA算法,算法性能更好。

4 结 论

1) 针对含分布式电源配电网状态估计优化模型的特点,提出了求解该模型的鸽群优化算法,确定种群规模和迭代步数后,通过磁场算子阶段和地标算子阶段,在反复迭代搜索后,于解空间获取优化问题的最优解。

2) 算例表明,鸽群优化算法具有易于理解、易于编程实现、收敛速度快等优点。

3) 由均方根误差和平均绝对误差计算结果可以看出,相较于遗传算法,鸽群优化算法计算精度更高,表明采用这一优化算法进行含分布式电源配电网状态估计是可行的。为配电网研究人员提供了一种新的状态估计方法。