Dual-porosity model of rate transient analysis for horizontal well in tight gas reservoirs with consideration of threshold pressure gradient ＊

Li-na Cao (曹丽娜), Xiao-ping Li (李晓平), Ji-qiang Zhang (张芨强), Cheng Luo (罗诚),Xiao-hua Tan (谭晓华)

1.China ZhenHua Oil Co.Ltd., Beijing 100031, China

2. State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation, Southwest Petroleum University,Chengdu 610500, China

3.CNOOC Zhanjiang Co.Ltd., Zhanjiang 524057, China

4. Geological Exploration and Development Research Institute of CNPC Chuanqing Drilling Engineering Ltd.,Chengdu 610056, China

Abstract: Most researches of the threshold pressure gradient in tight gas reservoirs are experimental and mainly focus on the transient pressure response, without paying much attention to the transient rate decline.This paper establishes a dual-porosity rate transient decline model for the horizontal well with consideration of the threshold pressure gradient, which represents the non-Darcy flow in a fracture system.The solution is obtained by employing the Laplace transform and the orthogonal transform.The bi-logarithmic type curves of the dimensionless production rate and derivative are plotted by the Stehfest numerical inversion method.Seven different flow regimes are identified and the effects of the influence factors such as the threshold pressure gradient, the elastic storativity ratio, and the cross flow coefficient are discussed.The presented research could interpret the production behavior more accurately and effectively for tight gas reservoirs.

Key words: Rate transient analysis, horizontal well, dual-porosity, threshold pressure gradient, tight gas reservoirs

Introduction

With the natural gas exploration and development, more and more low permeability tight gas reservoirs were found all over the world with characteristics such as large reserves, difficult development,and low productivity.In the tight gas reservoir (TGR)development, the rate transient analysis (RTA) is used as an effective method for obtaining the seepage parameters of the wells and the formation and the monitoring reservoir dynamics.The production decline was firstly proposed by Arps, and gradually modified and studied by Fetkovich, Palacio and Blasingame, and Agarwal et al.

Studies of the rate transient analysis for unconventional resources were extensive.Zeng and Zhao[1]proposed an approximate equation to analyze the transient pressure behavior of a well in a reservoir with multiple permeability anomalies.Ozkan et al.[2]obtained a new Laplace-domain solution for the slightly-compressible fluid flow in the 3-D dualpermeability media, in which the horizontal well operates in a constant rate of production.Clarkson and Pedersen[3]focused on the single-phase flow associated with undersaturated black oil reservoirs and analyzed the simulated cases of multi-fractured horizontal wells completed in single porosity reservoirs,as well as naturally-completed horizontal wells in transient dual porosity reservoirs.Yao et al.[4]established a semi-analytical model to study the transient pressure behavior of multi-stage fractured horizontal wells in a rectangular reservoir.Xu et al.[5]modeled the un-stimulated regions as a dual porosity system, and obtained curves of a more general type to identify the linear flow and the transition flow alternately.Tan and Li[6]proposed a transient flow model of tree-shaped fractal reservoirs by embedding a fracture network simulated by a tree-shaped fractal network into a matrix system.Xu et al.[7]proposed a composite elliptical mathematical model to analyze the pressure transient and rate transient behaviors in tight oil/gas reservoirs with a simulated reservoir volume (SRV).Tan et al.[8]established a simulation method for the permeability based on the multiple fractal model to establish a relationship between the pore distribution and the permeability of porous media.Xu et al.[9]developed a modified off-center well model which was coupled in the discrete fracture model (DFM) to predict the production performance of dendritic-like stimulated horizontal wells.Wei et al.[10]proposed a numerical model and the solution was obtained using control volume finite element method and the fully implicit method.Blasingame production decline-type curves of the infinitely conductive MFHW were plotted through computer programming.

For most TGRs, the permeability is extremely low.As a most effective and popular choice, a horizontal well is widely used to economically develop the tight formation.So many studies were related to the horizontal well seepage theory.As a number of tight oil/gas reservoirs are naturally fractured with dual-porosity characteristics, the seepage problems about dual media were extensively studied.Lian et al.[11]proposed a model coupling a reservoir and a fractured horizontal well to analyze factors that affect the productivity of the fractured horizontal well.Nie et al.[12]proposed a good semianalytical model for the horizontal well testing and the rate decline interpretation.They took the dual-porosity and the dual-permeability into account and analyzed the significant differences between the dual permeability and single permeability models.Zeng et al.[13]proposed a novel fractured horizontal well model for spindle shaped ultralow permeability reservoirs.Yao et al.[14]presented a semi-analytical model based on the Green's functions and the source/sink method to facilitate the transient pressure analysis for a multistage fractured horizontal well in a closed box-shaped reservoir.

Moreover, due to the low or even ultra-low permeability and porosity of the tight formation, the influence of the threshold pressure gradient (TPG)cannot be ignored.Guo et al.[15]established a transient pressure analysis mathematical model of horizontal gas wells, taking the TPG into account for tight gas reservoirs.They studied the transient pressure behavior but did not pay much attention to the production rate decline.By deriving the steady productivity equations for fractured wells in tight gas reservoirs for low-velocity non-Darcy flows, Song et al.[16]came to a conclusion that the influence of the TPG on the volumetric flow rate of a gas well cannot be neglected.Ding et al.[17]suggested that the TPG is increasing along with the decrease of the pore pressure and defined new concepts of the “TPG Rising Cone” and the “TPG Sensitivity Coefficient” to characterize the dynamic TPG of tight gas reservoirs.Xu et al.[18]carried out TPG and stress sensitive experiments and investigated the existing condition of the TPG and the permeability modulus.Taking not only the TPG but also the quadratic pressure gradient term into consideration, Liu and Yao[19]proposed a moving boundary model in low-permeability reservoirs to be solved by numerical methods due to its strong nonlinearity.Wu et al.[20]began with analysis of capillary microscopic model, core stress sensitivity experiments, and non-Darcy percolation experiments so that a novel productivity model and productivity evaluation model which couples stress sensitivity and threshold pressure gradient were proposed.

From the above literature review, it is seen that most studies of the threshold pressure gradient for dual-porosity tight gas reservoirs were experimental or put much emphasis on the transient pressure behavior, without taking the TPG into account for the rate transient decline of tight reservoirs.On the basis of the Warren-Root model, this paper derives a transient production rate decline analysis model for horizontal wells in dual-porosity TGRs with the consideration of the TPG.The mathematical model solution is obtained by employing the Laplace transform and the orthogonal transform.The bi-logarithmic type curves of the dimensionless production rate and derivative are plotted by the Stehfest numerical inversion method.The characteristics of the transient rate decline behavior are analyzed and different flow regimes are identified by the type curves.Effects of related parameters are discussed as well, which has an important significance in understanding the transient flow behavior and exploiting the TGR efficiently.

1.Physical model description

A TGR is composed of a matrix system and a fracture system with relatively independent physical properties.For a single horizontal well in a production TGR (Fig.1), the gas flows from the matrix system to the fracture system, and then flows to the horizontal wellbore due to the pressure drop between the wellbore and the fracture (Fig.2).To make the mathematical model more tractable and easy to understand,the following assumptions are made:

(1) The reservoir top and bottom boundaries are impermeable and the lateral boundary is infinite.The initial formation pressure ispi, with the same value everywhere.

(2) The dual-porosity system is based on the Warren-Root model.The matrix and fracture porosities, respectively, aremφandfφ, and the permeabilities areKmandKf.

Fig.1 Sketch map of horizontal gas well in dual-porosity formation

(3) The pore media are homogeneous and isotropic, and consist of equal parallel arrayed rectangular matrixes.

(4) The fractures are anisotropic and consist of a set of continuous, evenly and orthogonal systems.The horizontal and vertical permeabilities, respectively,areKfh,Kfv.

(5) The horizontal section of the well is parallel to the closed top and bottom boundaries, and its location is unlimited and represented byzw.

(6) The single-phase gas flows to the well through fractures only and obeys the non-Darcy law with consideration of the TPG.And the gas flow in the matrix is neglected due to the fact thatKf≫Km.A pseudo-steady cross flow occurs between the matrix and the fractures.This model is commonly called the dual-porosity and single-permeability model.

(7) The slightly compressible gas has a constant viscosity and compressibility coefficient, and the gas flow is under an isothermal condition.

(8) The influence of gravity and capillary force are ignored, both the wellbore storage effect and the skin effect are taken into consideration.

2.Mathematical model establishment

2.1 Governing flow equations in dual-porosity system

In the cylindrical coordinate system, the generalized forms of the mass conservation equation for the single phase fluid flow in the dual-medium are as follows:

For fracture system

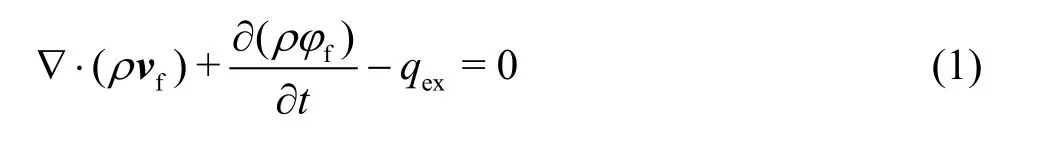
For matrix system

Cross flow equation

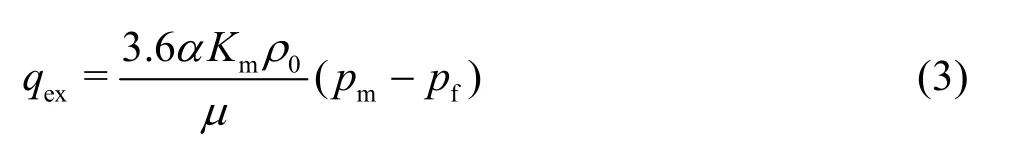
The permeability of the matrix system segregated and surrounded by fractures is usually several orders of magnitudes smaller than that of the fracture system, therefore the flow in the matrix system can be neglected and the matrix can be considered as an evenly distributed source that releases the gas into the fractures.So Eq.(2) can be simplified as:

In view of the fact that the flow of the gas in the fractures obeys the non-Darcy law which takes the TPG into account, the motion equation can be expressed by[21]:

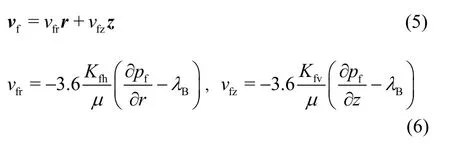
whereBλis the threshold pressure gradient.

The gas state equation which is the relationship between the density and the pressure is

where the density of the natural gas can be expressed according to the equation of state for the real gas

The porous rock is elastic and compressible and its state equations are as follows:

Combining Eq.(1) and Eqs.(3)-(10), and simplifying the new equation, we can obtain the real gas governing partial differential equations taking the TPG into account:

where the total compressibility coefficient

The pseudo pressure is introduced as in the following formula:

wherep0is the reference pressure and can be freely selected.Therefore:

In addition, the cross flow item can be transformed from the pressure form into the pesduo-pressure form as

Inserting Eqs.(15)-(19) into Eqs.(11)-(12), and multiplying both sides by 2 |Kfh, we obtain:

Commonly, the value ofBλis in an order of magnitude of 10‒3, which means thatBλis small.As a quadratic gradient term, the product term ofBλand(∂/∂r)(p|μZ) or (∂/∂z)(p|μZ) can be ignored for the sake of simplifying the calculation.Therefore Eq.(20) can be turned into

The pseudo threshold pressure gradient is introduced as follows:

Equation (22) can be rewritten as

2.2 Dimensionless partial differential model of seepage

According to the dimensionless definitions, the dimensionless seepage differential equations converted from Eqs.(21), (24) are as follows:

Initial condition

Inner boundary condition

Infinite lateral boundary condition

Closed top and bottom boundaries

To sum up, the seepage partial differential mathematical model for the horizontal well in the dualporosity TGR is expressed by Eqs.(25)-(31).

3.Mathematical model solution

It is worth noting that Eq.(25) is strongly nonlinear and the exact solution is hard to obtain by a conventional method.For the initial boundary value problem, the first step is make the Laplace transform with respect to the time variable, and the second step is to make the orthogonal transform with respect to the spatial variable, thus to reduce the nonlinear degree of the problem for the final solution.

3.1 Laplace transform

Introduce the Laplace transform formiD(rD,zD,tD) fromtDtos(i=f,m), defineas the Laplace transformation function ofmiD, that is

The dimensionless seepage mathematical model in Laplace domain can be written as follows:

3.2 Orthogonal transform

Define the integral transform about the space variablezDas follows

By solving a Sturm-Liouville eigenvalue problem relating toZ(zD,μ) which is composed by corresponding Sturm-Liouville equation and boundary conditions, the integral transform kernel can be determined as follow:

Introduce the orthogonal transform about variablezDwith eigenfunctions c osnπzDas the kernel,letdenote the orthogonal transform function of, that is

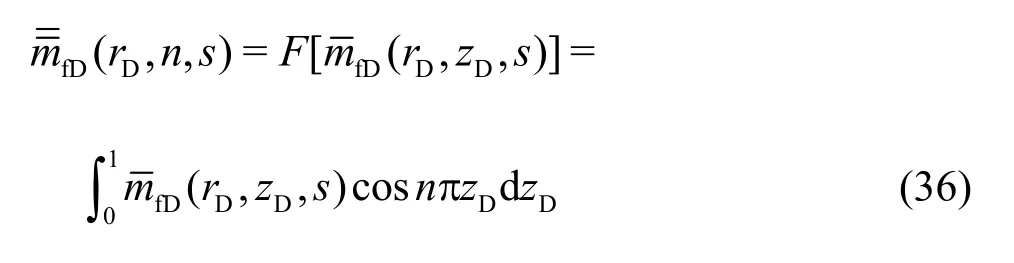
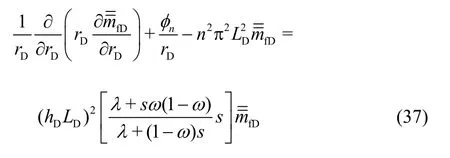
The inner boundary condition is orthogonally converted as

Take the orthogonal transform on the outer boundary condition of model (33)

Simultaneous Eqs.(37), (38) and (39) for a mathematical model aboutas follows:

3.3 Model solutions

To solve the model (40), we consider two cases with regard to the value ofn.To simplify the solving process, let:

(1) Ifn≠0,φn=0, the basic differential equation of model (40) can be converted into a zero order modified Bessel equation.The derivation process is shown as the following steps.

whereυ=0,υmeans the order number of modified Bessel equation.The general solution of the equation is written as

whereI0is the first kind of zero order modified Bessel function,K0is the second kind of zero order modified Bessel function,A,Bare constants.

(2) Ifn=0,the basic differential equation of model (40) is inhomogeneous due to its free term is not equal to zero.The particular solution can be expressed by Green functions.So the general solution is shown as

Combining Eq.(39) infinite outer boundary condition andI0(∞)=∞, we can obtainA=0.So Eq.(45) is rewritten as

Combining Eq.(38) inner boundary condition and properties of Bessel functions, ifz→0, thenI1(z)≌0, soB= cosnπzwD/2s.TakeBinto Eq.(47) and yield

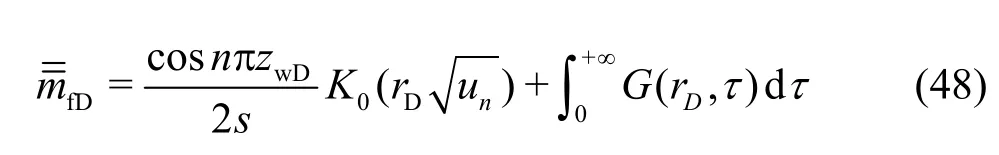
According to the complete orthogonal property of eigenfunctions system (c osnπzD,n= 0,1,… + ∞),the inverse orthogonal transformation can be expressed by

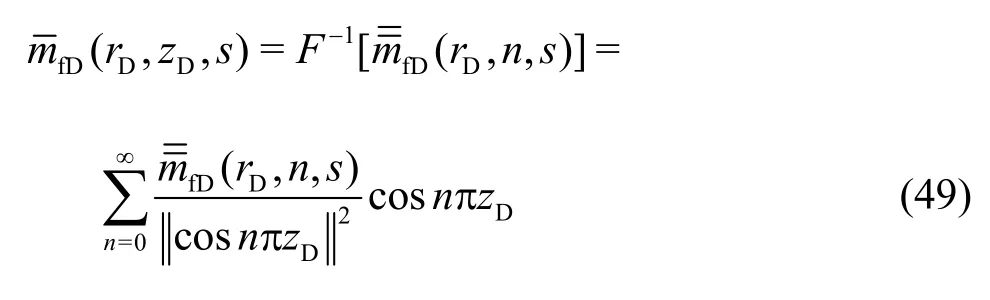
Therefore, the pseudo-pressure solution in Laplace domain from Eq.(48) is like this

According to the source function idea method, letyD=0, using Eq.(50) to mark the point-source solution, compute the integral for horizontal section of wellbore, we can obtain the bottom hole pseudo pressure solution expression as follows with considering the effect of TPG.

Employing Duhamelʼs theorem and the superposition principle to incorporate wellbore storage coefficient and skin factor into well response, the pseudo pressure expression can be rewritten as

So the dimensionless wellbore flow rate equation for the constant-pressure production case in tight gas reservoirs can be obtained according to the relationship between dimensionless pressure and rate in Laplace space (van Everdingen and Hurst (1949))

From Eqs.(51)-(53), we can obtain the horizontal well dimensionless rate solution under the influence of the TPG for dual-porosity tight gas reservoirs.

4.Analysis of type curves

The solutions of the dimensionless pseudopressure and the production rate in real space can be obtained by employing the Stehfest numerical inversion algorithm (Stehfest (1970)).Intuitively, the type curves characterize the process and flow behaviors in reservoirs.

4.1 Type curves of pseudopressure response and rate transient decline

Figure 3 clearly shows the transient pseudopressure response of the horizontal well in a dual-porosity TGR, which includes seven flow regimes.Regime 1 is the pure wellbore storage effect flow regime, the curves of the pseudopressure and the derivative have the same trend in an upward sloping line as a conventional reservoir.Regime 2 is the skin effect transition flow regime; the transient pressure derivative curve is like a “hump”.Regime 3 is the early radial flow regime in the vertical plane; the pressure curve goes on to increase, and the derivative curve is shown as a level straight line, with a value related toLD.Regime 4 is the early linear flow regime; the pressure derivative curve is a straight line with a slope of 0.5.Regime 5 is the mid-term radial flow regime of the fracture system, the pseudopressure derivative be-haves as a horizontal line but the value is not 0.5 due to the effect of the TPG.Regime 6 is the cross flow regime of the dual-medium, the derivative curve is characterized by a concave shape, which is the typical response of the gas transfer from the matrix system to the fracture system.Regime 7 is the late whole radial flow regime of the matrix system and the fracture system, the derivative curve is like an up-wrap instead of a “0.5 level line” also because of the TPG.

Fig.3 Type curv es of pseu dopressure response in dual-porosity tight gas reservoir(λm BD =0.5, CD=10-6, S=0.1,LD =5,hD=10, λ = 0.001, ω=0.1)

The whole production rate transient decline behavior of the horizontal well in a dual-porosity TGR is plotted in Fig.4.Correspondingly, seven flow stages can be identified as follows:

Stage 1: Pure wellbore storage effect flow regime.This stage occurs in the early time, the curves of the production rate and derivative have the same trend of a downward sloping line as the conventional reservoir.This period is controlled by the gas stored in the wellbore.

Stage 2: Skin effect transition flow regime.The drop degree of the production rate curve changes slowly and the rate derivative curve continues to decline into a concave shape, which corresponds to the hump of the transient pressure derivative curve.This stage reflects the combined action of the skin and wellbore storages.

Stage 3: Early radial flow regime in the vertical plane.The production rate curve goes on to decrease,and the derivative curve is shown as a level straight line, whose value is related toLD.This period reflects the radial flow feature perpendicular to the horizontal axis before the pressure wave propagates to the top and bottom outer boundaries.

Stage 4: Early linear flow regime.The curve of the production rate derivative shows a slight upward trend.This period reflects the linear flow feature around fractures.The decline of the rate curve is not significant due to the sufficient gas source in the fracture system.The influence of the TPG can also be seen from this period.

Stage 5: Mid-term radial flow regime of fracture system.The curves of the production rate and derivative manifest as two parallel lines with the same slope.In this stage, the free gas stored in the fracture system flows towards the horizontal well radially and the production is mainly dominated by the depletion of the natural fracture system.

Stage 6: Cross flow regime of dual-medium.The significant feature of this period is the concave shape of the rate derivative curve.With the gas being produced continuously, the gas stored in the matrix starts to flow towards the fractures because the pressure drop between the fracture system and the matrix system is large enough to cause the gas transfer.

Stage 7: Late radial flow regime of whole system.It is characterized by a drop line on both the production rate and its derivative curves.The production rises to a unified state of a dynamic balance and the energies of both systems are consumed simultaneously.

Fig.4 Type cur ves of ra te transient decline in dual-porosity tight gas reservoir(λm BD =0.5, CD=10-6, S=0.1,LD =5, hD=10,λ= 0.001, ω=0.1)

4.2 Sensitivity analysis of rate transient decline performance

Figure 5 shows the effect of the threshold pressure gradient on the rate transient decline type curves.It indicates that the TPG mainly plays its role in the period from the early linear flow regime to the late radial flow regime of the whole system.The greater the TPG is, the worse the reservoir property is, the more difficult the fluid flows, and the lower the production rate is.In addition, the rate derivative curves goes downward with the increase of the TPG.

Figure 6 reflects the effect of the elastic storativity ratio on the rate transient decline type curves.Theωrepresents the relative capacity of the reserves of the gas storage in the fracture system.From this figure we can intuitively see that the elastic strorativity ratio has a major influence on the part from regime 3 to regime 6.Especially in the cross flow period of the rate derivative curve, a smaller elastic strorativity ratio leads to an earlier starting time of this stage, a deeper concave V-shape and a longer time when the inter-porosity flow lasts.

Fig.5 Effect of threshold pressure gradients on rate transient declinecurves(CD =10-6,S=0.1,LD=5,hD=10,λ= 0.001,ω=0.1)

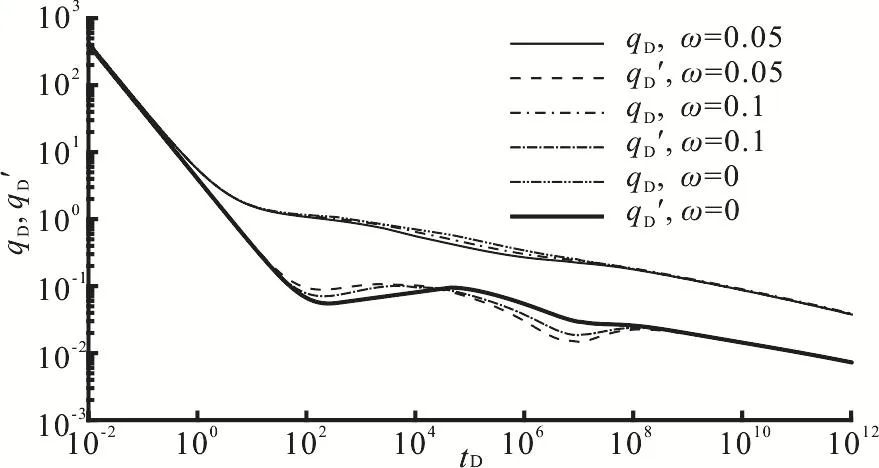
Fig.6 Effect of elastic storativity ratios on rate transient decline curves(λm BD =0.5,CD=10-6,S=0.1,LD=5,hD=10,λ= 0.001)

Fig.7 Effect of cross flow coefficients on rate transie nt decline curves(λm BD =0.5,CD=10-6,S=0.1,LD=5,hD=10,ω=0.1)

Figure 7 shows the effect of the cross flow coefficient on the rate transient decline type curves.For the rate derivative curve, the larger the cross flow coefficient is, the earlier the cross flow regime starts.Even sometimes when the radial flow stage in the mid-term fractures has not finished yet, the interporosity flow is already started.On the production rate curve, according to the definition ofλ, the smaller theλis, the greater the permeability property difference between the matrix and the fractures is, the more difficult the cross flow happens, so the lower the production rate is.

Figure 8 shows the effect of the horizontal section length on the rate transient decline type curves.With the increase of the horizontal section length,both the production rate curve and the rate derivative curve go up.It is because the horizontal well represents the control volume of the well.The longer the horizontal section is, the larger the gas drainage area will be.The resistance of the gas flow becomes relatively smaller and the corresponding production rate will be greater.

Fig.8 Effect of horizontal section lengths on rate transient decline curves (λm BD =0.5, CD=10-6, S=0.1, hD=10, λ = 0.001,ω=0.1)

Fig.9 Effect of reservoir thicknesses on rate transie nt decline curves(λm BD =0.5,CD=10-6,S=0.1,LD=5,λ= 0.001, ω=0.1)

Figure 9 indicates the effect of the reservoir thickness on the rate transient decline type curves.As we can see, the change of the reservoir thickness has a significant influence on the type curves of the regime 3.When the reservoir thickness becomes greater, the pressure wave takes more time to propagate to the top and bottom boundaries.Consequently the early vertical radial flow regime (stage 3) will last longer.Moreover the appearance of the next flow periods(including the fracture system flow, the inter-porosity flow between the matrix and the fractures, and the whole system radial flow) will be postponed.

5.Conclusions

In this paper, a dual-porosity model for a horizontal well in a tight gas reservoir with considerations of the threshold pressure gradient is established, and the rate transient decline behaviors under the effects of the relative influence factors are analyzed.The following conclusions can be drawn:

(1) The TPG mainly affects the part from the early linear flow regime to the late radial flow regime of the whole system in the type curves of the rate transient decline.A larger TPG can obviously cause a downwarping of both the production rate and its derivative curves.

(2) A smaller elastic strorativity ratio leads to a deeper concave V-shape of the rate derivative curve and a longer time that the inter-porosity flow lasts.Besides, the rate derivative curve has features that the larger the cross flow coefficient is, the earlier the cross flow regime starts.

(3) With the increase of the gas drainage area caused by a larger horizontal section length, both the production rate curve and the rate derivative curve go up.In addition, the greater the reservoir thickness is,the longer the early vertical radial flow regime lasts.

Acknowledgment

This work was supported by the supports of PetroChina Innovation Foundation (Grant No.2016D-5007-0209).