基于改进花授粉算法和极限学习机的 锅炉NOx排放优化
牛培峰, 李进柏, 刘 楠, 李国强, 王荣彦
(1.燕山大学 工业计算机控制工程河北省重点实验室,河北秦皇岛 066004; 2.燕山大学 材料科学与工程学院,河北秦皇岛 066004)
电厂锅炉是大气污染物NOx的主要排放源之一[1]。NOx易形成雾霾和酸雨,不仅污染环境而且会造成一定的经济损失。因此,如何降低NOx排放是电厂面临的重要课题。目前,电厂控制NOx排放的方法主要有尾部烟气脱硝和燃烧优化技术[2]。烟气脱硝技术虽然在一定程度上能降低NOx排放质量浓度,但是需要安装额外设备和后期维护,操作成本较高。燃烧优化技术运行成本低,通过优化锅炉燃烧过程,使NOx排放质量浓度达到期望目标。
锅炉燃烧优化技术的基础是建立一个精确的燃烧特性模型,并以此模型为前提,利用智能算法优化锅炉运行时的可调参数,给出操作量最佳值,实现锅炉清洁高效运行。很多学者致力于研究电站锅炉燃烧优化技术,并取得了不错的成果。李庆伟等[3]利用集成支持向量机建立600 MW四角切圆煤粉炉NOx排放特性模型,并采用改进的粒子群算法优化配风方式以降低NOx排放质量浓度。张文广等[4]采用自适应模糊推理辨识方法建立循环流化床锅炉NOx排放特性模型,然后利用果蝇优化算法对锅炉运行工况进行优化,降低了NOx排放质量浓度。余廷芳等[5]利用BP神经网络模型建立燃煤锅炉NOx排放和热效率特性模型,然后利用遗传算法优化燃烧工况,降低了NOx排放质量浓度并提高了热效率。
极限学习机(ELM)[6]是一种新型单层前馈神经网络,只要确定输入权值和隐层阈值,就可以通过最小二乘法确定网络参数,避免了因反复迭代陷入局部最小的问题,具有很强的拟合能力和泛化能力,能用于燃煤锅炉NOx排放质量浓度预测建模。但是ELM随机生成的输入权值和隐层阈值会影响模型性能,可以将权值和阈值的选取作为一个优化问题,借助智能优化算法进行寻优。花授粉算法(FPA)[7]是一种新型启发式算法,因结构简单、可调参数少、鲁棒性好被应用于无线电定位[8]、特征选择[9]和光伏模块参数估计[10]等工程领域。但算法中固定转换概率和局部随机搜索也会导致算法全局搜索与局部搜索能力失衡,搜索精度低。
笔者首先针对FPA收敛精度、搜索过程中全局搜索与局部搜索能力失衡等不足,在局部搜索中引入一种基于适应度值的步长,在全局搜索和局部搜索转化过程中构造动态自适应转换概率,提出改进的花授粉算法(AFPA)。然后以某电厂330 MW燃煤锅炉运行数据为基础,采用ELM建立 NOx排放特性模型,由于随机权值和阈值的影响,利用AFPA对ELM的权值和阈值进行优化,建立更加精确的NOx排放特性模型。在该模型的基础上,利用AFPA对锅炉运行时可调参数进行调整,以降低燃煤锅炉NOx排放质量浓度。
1 极限学习机
ELM的核心就是将单隐层神经网络的训练学习过程转化为求解线性最小二乘问题,然后通过MP广义逆计算出输出权值。简单表述如下:

每一个观测样本的输出为:
(1)
上述方程可简写为:
Hβ=T
(2)
其中,
(3)

(4)

(5)
式中:H为隐层输出矩阵;w1,…,wm为随机输入权值;b1,…,bm为隐层阈值。
输出权值β可以通过下式计算得到:
(6)
式中:H+为H的MP广义逆。
ELM的学习过程如下:(1)确定隐层节点数,并选择隐层激励函数;(2)随机初始化输入权值W和隐层阈值B;(3)按照式(3)计算出隐层输出矩阵H;(4)按照式(6)计算出输出权值β。
2 改进的花授粉算法
2.1 花授粉算法
FPA受启发于自然界中植物花朵传粉过程,其搜索过程分为全局搜索和局部搜索,二者转换概率由常数P控制。
全局搜索的位置更新变化公式为:
(7)

由于昆虫能以各种步长移动一大段距离,Levy飞行可以有效模拟这种特性。L(λ)>0,并且
(8)
式中:Γ(λ)为标准伽马函数;s和s0均为步长。
局部搜索的位置更新变化公式为:
(9)

2.2 改进的花授粉算法
FPA虽然具有良好的寻优能力,但也存在寻优精度不足和易陷入局部最优等缺点。针对FPA的不足,进行了如下2处改进。
(1)FPA中P为固定常数,易导致在迭代过程中算法的开采能力与探索能力失衡。为了平衡FPA全局搜索与局部搜索的能力,提出自适应转换概率:
(10)
式中:N为最大迭代次数,FPA中固定概率取0.8时,算法表现良好,故常数仍取0.8。P值随着算法迭代次数的增加而增大,使得算法前期倾向于全局搜索,而后期倾向于局部搜索,有效地平衡了算法的开采能力与探索能力。
(2)FPA中局部搜索的实质是在解空间的随机游走,易陷入局部最优。为改善局部搜索能力,提出一种基于适应度值的步长对局部搜索方案进行改进的方法。该步长表达式如下:
(11)
式中:ft和ft-1分别为当前适应度值和前一次迭代的适应度值,且当ft-1为0时,W=1。
于是,局部搜索的位置更新变化公式可改写为:
(12)
W反映了前一次迭代对下一次迭代的修正。当前一次迭代适应度值改变较大时,提高前一次解在当前迭代中所占比重;当前一次适应度值改变较小时,降低前一次解修正比重。W随着适应度值的变化不断调整,避免算法在局部迭代中陷入局部最小。
3 燃煤锅炉优化模型的建立
锅炉燃烧系统存在多个变量,各个变量之间相互耦合,存在复杂的非线性关系,很难用传统的方法建立精确的锅炉燃烧特性模型。ELM是一种新型的建模方法,无需了解锅炉燃烧系统的运行状况,只要根据锅炉运行的历史数据就可建立锅炉燃烧特性的黑箱模型。ELM随机给定的输入权值和隐层阈值会影响模型的预测精度,权值和阈值的选择可以看成是一个简单的优化问题,利用AFPA对输入权值和隐层阈值进行寻优,以确保模型的性能。
3.1 数据样本
在燃煤锅炉燃烧过程中,影响NOx排放的因素很多,需要根据NOx排放质量浓度与各个变量的关联度来确定模型输入参数。以某电厂330 MW八角双切圆燃煤锅炉为研究对象,该锅炉配备4台磨煤机、4台排粉机和32台给粉机,燃烧器采用三级点火方式。以集散系统(DCS)采集的20组数据为基础,选用锅炉负荷(1个)、给煤机转速(4个)、二次风速(5个)、燃尽风挡板开度(3个)、炉膛温度(1个)、空气预热器出口烟气平均含氧体积分数(以下简称含氧量,1个)、煤质特性(7个)和一次风速(4个)共26个对NOx排放影响关联度较大的变量作为输入,以NOx排放质量浓度作为输出。20组数据分为训练集和测试集2个部分,训练集有17个样本(即样本1~样本17)和测试集有3个样本(即样本18~样本20)。
3.2 参数优化和模型建立
在利用AFPA对ELM参数进行寻优过程中,AFPA参数设置如下:种群数设置为20,迭代次数为200,由于输入权值和隐层阈值的最小值和最大值均为-1和1,所以解的上下限设置为[-1,1]。ELM模型神经元个数为30,隐层激励函数为“sigmoid”,详细表达式为:
(13)
由于数据样本较小,为了最大程度地利用样本信息和防止发生过拟合现象,优化ELM参数时,对训练集的17个样本进行“留一法”处理,即每次选择16个样本作为训练数据,剩下一个样本作为预测数据,循环17次遍历所有训练集样本。以训练数据和预测数据的均方根误差之和作为优化目标函数,在200次迭代中得到最小优化目标函数的解,作为最优权值和阈值参数带入ELM。优化目标函数定义如下:
f=f1+f2
(14)
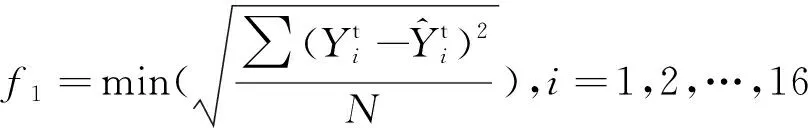
(15)
(16)

在确定最优参数后,先将训练集17个样本代入ELM,建立锅炉NOx排放特性模型;然后将测试集3个样本输入所建模型,得到NOx排放质量浓度的预测值,并与实际NOx排放质量浓度进行对比,测试模型的预测精度。
3.3 模型仿真结果分析
图1给出了训练集17个样本NOx排放质量浓度实际值与预测值的对比。由图1可知,预测值能够很好地跟踪实际值,模型拟合效果较好。图2给出了测试集3个样本NOx排放质量浓度实际值与预测值的对比。由图2可知,对于未知样本,所建模型能够对NOx排放质量浓度进行预测,并且预测值与实际值相差不大,模型具有很好的预测能力和泛化能力。
为了进一步验证模型性能,采用BP神经网络和基本ELM根据相同的数据建立锅炉NOx排放特性模型,并进行对比。ELM模型参数与第3.2节相同,输入权值和隐层阈值是随机给定的。BP神经网络模型采用26-26-35-1的结构,各层传递函数均采用tansig函数,表1给出了3个模型对测试集样本NOx排放质量浓度的预测结果。
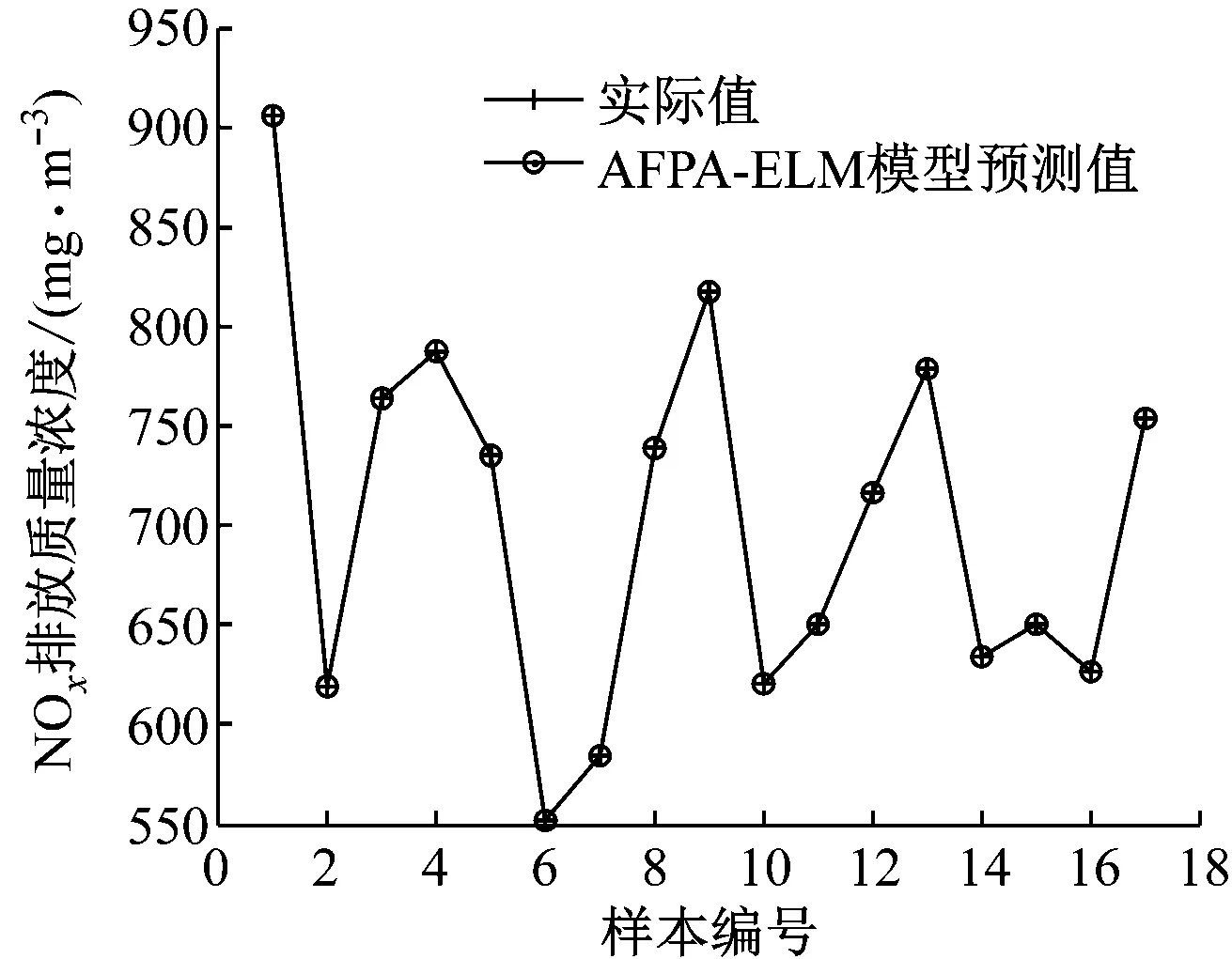
图1 训练集预测值与实际值的对比
Fig.1 Comparison of training set between predicted results and actual measurements
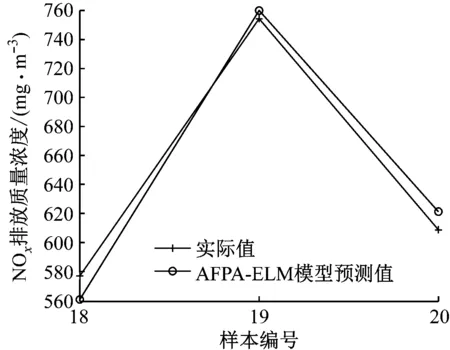
图2 测试集预测值与实际值的对比
Fig.2 Comparison of test set between predicted results and actual measurements

表1 测试集样本预测结果对比Tab.1 Comparison of test set predicted results
由表1可以看出,AFPA-ELM模型、ELM模型和BP神经网络模型都能对燃煤锅炉NOx排放质量浓度进行预测,就预测结果的精度而言,AFPA-ELM模型和ELM模型的预测精度优于BP神经网络模型,AFPA-ELM模型的预测值相比于ELM模型更逼近实际值。AFPA-ELM模型对样本18~样本20的预测相对误差分别为-2.80%、0.64%和2.02%,相对误差比另外2种模型小。结合图1、图2和表1可以看出,AFPA-ELM模型对训练集样本和测试集样本的预测效果均良好,为实现锅炉燃烧优化提供了基础。
4 NOx排放质量浓度优化
以所建NOx排放特性模型为基础,选用DCS中可以直接调节的变量:给煤机转速(4个)、二次风速(5个)、燃尽风挡板开度(3个)、含氧量(1个)和一次风速(4个)共17个参数作为可调参数,利用AFPA对这17个参数进行寻优,剩下的9个变量作为不可调节参数保持不变。将这17个参数定义为一个待优化变量x=[x1,x2,…,x17],其中x1~x4为4个给煤机转速,x5~x9为5个二次风速,x10~x12为3个燃尽风挡板开度,x13为含氧量,x14~x17为4个一次风速。优化目标为降低NOx排放质量浓度,优化目标函数描述为:
minfNOx(x)=f(x)
(17)
为了保证优化结果的可靠性和可行性,根据现场采集数据的最大值和最小值及文献[11]确定17个优化参数的约束范围,各参数约束范围见表2。

表2 参数约束范围Tab.2 Parameter constrains
随机抽出样本3和样本13,采用AFPA对其可调参数进行优化,以降低NOx排放质量浓度。为了验证AFPA的有效性,利用FPA对相同样本进行优化,2种算法的参数设置完全相同,经过多次实验,最大迭代次数设置为100,以100次寻到的最小值作为NOx排放质量浓度的最优值,根据对应的解确定17个可调参数的值。2种算法对样本3的迭代曲线见图3和图4,其优化结果见表3。

图3 AFPA对样本3的优化过程
Fig.3 Optimization process for sample 3 by AFPA

图4 FPA对样本3的优化过程Fig.4 Optimization process for sample 3 by FPA

表3 2种算法的优化结果Tab.3 Optimization results of two algorithms
由图3和图4可以看出,随着迭代次数的增加,NOx排放质量浓度逐渐下降,最后达到稳定。但AFPA所需迭代次数比FPA少,说明AFPA比FPA寻优速度快。由表3可知,相比于原始数据,采用FPA和AFPA优化后的NOx排放质量浓度都有一定幅度降低,其中采用AFPA优化后NOx排放质量浓度的降幅更加明显,这就说明相比于FPA,AFPA具有更好的寻优性能。对比优化结果可以发现,降低给煤机转速可以降低NOx排放质量浓度,但是若给煤量波动较大会影响锅炉负荷,在实际操作过程中,可以对给煤量进行微调。降低一次风速和二次风速使得NOx排放质量浓度降低,一次风量和二次风量减少使得煤粉充分燃烧的可能性降低,可以降低NOx排放质量浓度。燃尽风挡板开度增大,增加燃尽区风率使得燃烧器内过量空气系数降低,炉内平均火焰温度下降,减少了热力型NOx的生成,这与文献[12]现场实验结果一致。降低含氧量可以在很大程度上抑制煤中挥发分N向NO的转换过程,减少燃料型NOx的生成,这符合燃料型NOx产生机理。
5 结 论
为降低燃煤锅炉NOx排放质量浓度,首先针对花授粉算法的不足,提出改进的花授粉算法,并利用该算法优化ELM参数,建立330 MW燃煤锅炉NOx排放特性模型,相比于ELM模型和BP神经网络模型,所建模型具有更高的预测精度,可以对锅炉NOx排放质量浓度进行预测,为预测电站锅炉NOx排放质量浓度提供了一种新的方法。在该模型的基础上,分别利用花授粉算法和改进的花授粉算法对锅炉可调参数进行优化,2种算法优化之后NOx排放质量浓度都有所降低,但是改进花授粉算法优化后的效果更加明显,证明该算法是一种高效的算法。

