基于微透镜阵列匀束的激光二极管面阵抽运耦合系统分析∗
严雄伟 王振国 蒋新颖 郑建刚2) 李敏 荆玉峰
1)(中国工程物理研究院激光聚变研究中心,绵阳 621900)
2)(IFSA协同创新中心,绵阳 621900)
1 引 言
激光二极管(laser diode,LD)面阵具有高功率、高效率、长寿命的优点,广泛应用于高能固体激光器抽运源.由于单bar条功率和封装结构的限制,LD面阵的发光功率水平较低,目前只能达到kW/cm2量级,与高能固体激光器抽运强度的需求(约10 kW/cm2)相差较远[1,2];同时由于bar条的发光特性使得抽运光斑均匀性较差,直接影响了激光器的性能[3−5].这使LD面阵的抽运耦合缩束整形技术变得十分重要.
初期的高功率二极管抽运激光器多采用导光管(duct)作为抽运耦合器件[6−12],通过导光管内表面对抽运光的反射实现抽运光的汇聚,导光管耦合效率较高(可达90%),结构简单易于制作,主要缺点是经过耦合系统后光束的发散角增大,导光管出口的抽运光均匀性和可传输性较差[13,14].
微透镜阵列光束整形系统结构简单、使用灵活,成为LD面阵抽运耦合的新选择.文献[15—18]对基于微透镜阵列整形系统进行了原理上的分析,并使用发光二极管照明微透镜阵列获得了均匀光斑;黄峰等[19,20]通过光线追迹方法对空心导管、波导管、二元光学元件与微透镜阵列进行比较,其结论为微透镜阵列具有更好的匀化光束的能力;殷智勇等[21,22]研究了成像型和非成像型光束积分系统的光束匀化机理,发现成像型光束积分系统具有更好的匀化效果;刘志辉等[23,24]提出了一种用衍射微透镜阵列对LD面阵光束进行匀化的方法,解决了折射型微透镜阵列难于实现高填充因子、高精度面型的难题;余金清等[25]将微透镜阵列与长焦深菲涅耳透镜结合,对半导体激光器阵列光进行整形,获得长工作深度范围的均匀抽运场;雷呈强等[26,27]讨论了微透镜阵列误差对半导体激光匀化性能的影响.
上述研究开展了微透镜阵列光束整形的理论和实验研究,但对微透镜阵列匀束系统在LD面阵抽运耦合实际应用中的参数设计问题未开展细致研究.为了进一步发展高均匀性高功率LD面阵抽运耦合技术,本文基于几何光学和数理统计分析的方法,建立了微透镜阵列匀束系统的数学与物理模型,对微透镜阵列参数与最终耦合输出抽运场参数之间的关系进行分析,并开展实验对理论分析进行验证,从而为基于微透镜阵列匀束的LD面阵抽运系统的研究和设计提供指导.
2 微透镜阵列匀束原理与参数设计分析
基于微透镜阵列的匀束系统包括非成像型与成像型两种,因为成像型匀束系统具有更好的匀化效果,本文的研究集中于成像型微透镜阵列匀束系统.
成像型微透镜阵列匀束系统由两片串联的微透镜阵列(多个相同的微透镜单元呈阵列排布)和一个傅里叶透镜组成,如图1所示,两片微透镜阵列LA1和LA2形成多组平行的Kohler照明系统,第一片微透镜阵列将入射光束分割成大量的子光束,第二片微透镜阵列则与傅里叶透镜一起,将这些子光束的像重叠在傅里叶透镜焦平面处实现平顶型光强分布.匀束系统中微透镜阵列的各项参数(微透镜单元的形状、尺寸、焦距、阵列通光单元数等)对输出光场参数有不同的影响,下文将进行具体分析.

图1 成像型微透镜阵列匀束系统原理图Fig.1.Schematic of imaging microlens array system.
2.1 微透镜单元形状
为实现较高的系统传输效率,要求微透镜单元在阵列排布时具有高填充比.这是因为入射光束照射在微透镜单元上的光线才能被成像传输到焦平面指定位置,如果照射到微透镜之间的空隙,则该部分光线无法成像,造成效率损耗.在二维平面上能够实现100%填充比的规则图形主要有正方形、矩形、正六边形等,使用这些形状的微透镜单元组合为阵列,可以实现高传输效率.
由成像光路可知,在焦平面成像的光场形状与微透镜单元形状相似.激光器所需的LD面阵抽运场多为正方形或矩形,所以应用于LD面阵抽运系统的微透镜阵列单元多使用正方形或矩形单元.
2.2 微透镜单元F数
图1显示,两片阵列中微透镜单元大小相同,尺寸为PLA,微透镜单元焦距分别为f1,f2,两片阵列间距为a12,第二列微透镜阵列与傅里叶透镜间距为s,傅里叶透镜焦距为fFL,使用准直光入射时,根据理论推导,焦平面处光场尺寸使用一套成像型微透镜阵列匀束系统,通过调整微透镜阵列间距a12可以实现焦平面光场尺寸大小的调节.微透镜阵列匀束系统用于LD面阵抽运耦合时,可以通过调整微透镜阵列间距a12实现LD面阵抽运强度的调节,a12越大,抽运光场尺寸越小,抽运强度越大.
由于LD阵列自身的特性,其发射光线并非准直光,且快慢轴方向光线具有不同的发散角,使用微透镜阵列匀束系统进行抽运耦合时需要根据实际情况进行参数设计,文献[22]讨论了微透镜阵列间距a12=f1时非准直光的接收角问题.在实际应用时,为调节抽运场强度,a12与f1并不总是相等.对于微透镜阵列间距a12=f1的情况,选取单组微透镜单元的子孔径光线进行分析,如图2.
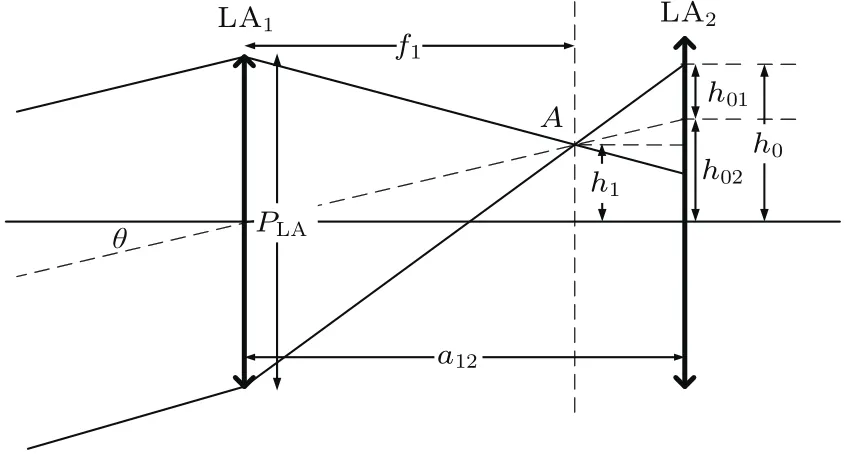
图2 单组微透镜单元子孔径光线分析Fig.2.Beam analysis of single microlens aperture.
设入射光束的最大角度为θ,微透镜单元尺寸为PLA,其经过LA1聚焦后像点A位于微透镜阵列LA1焦面上,像点A离轴量h1=f1tanθ,LA2被光线覆盖的最大范围为h0.根据图2中几何关系,由h0=h01+h02,h02/h1=a12/f1,

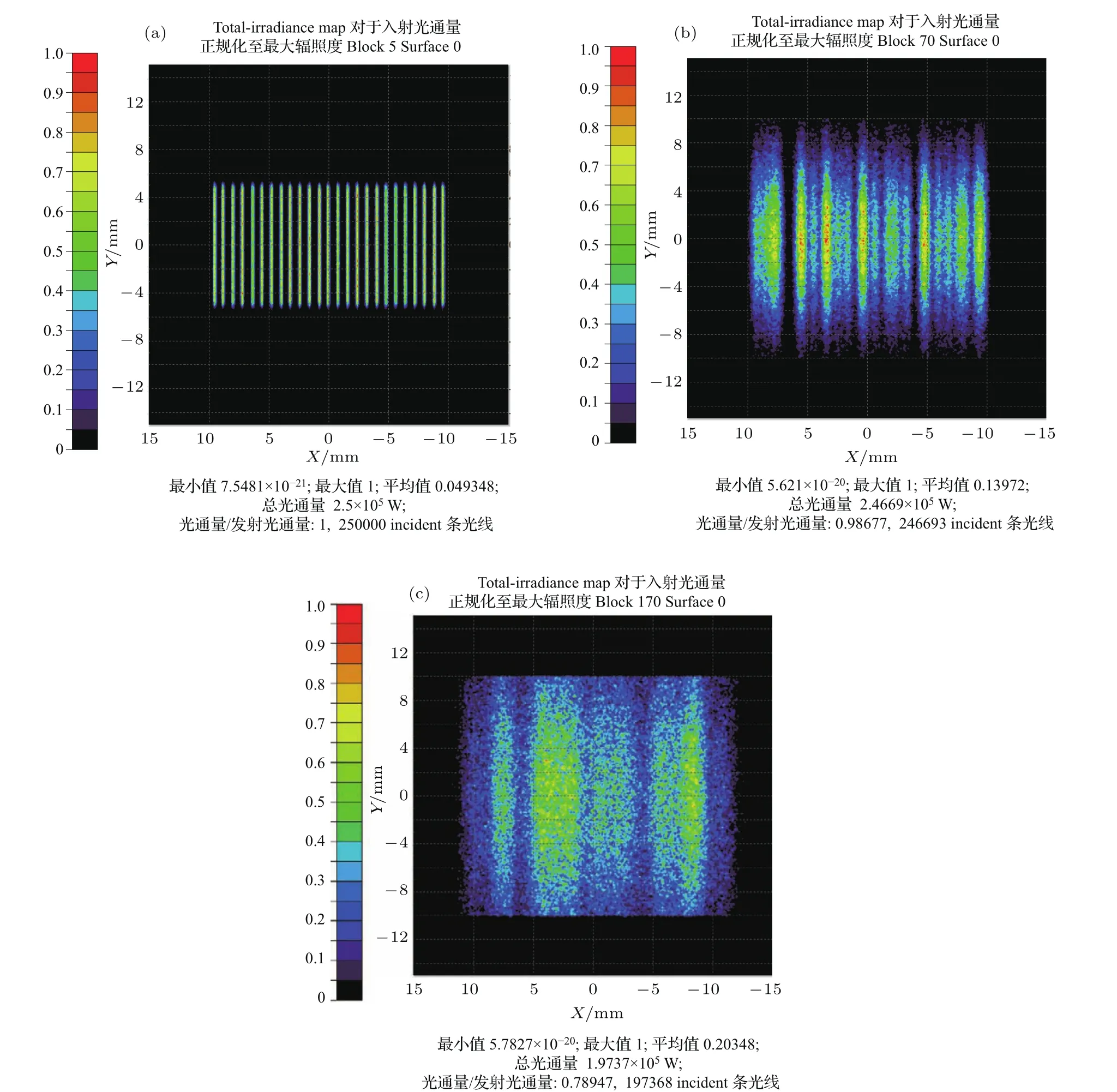
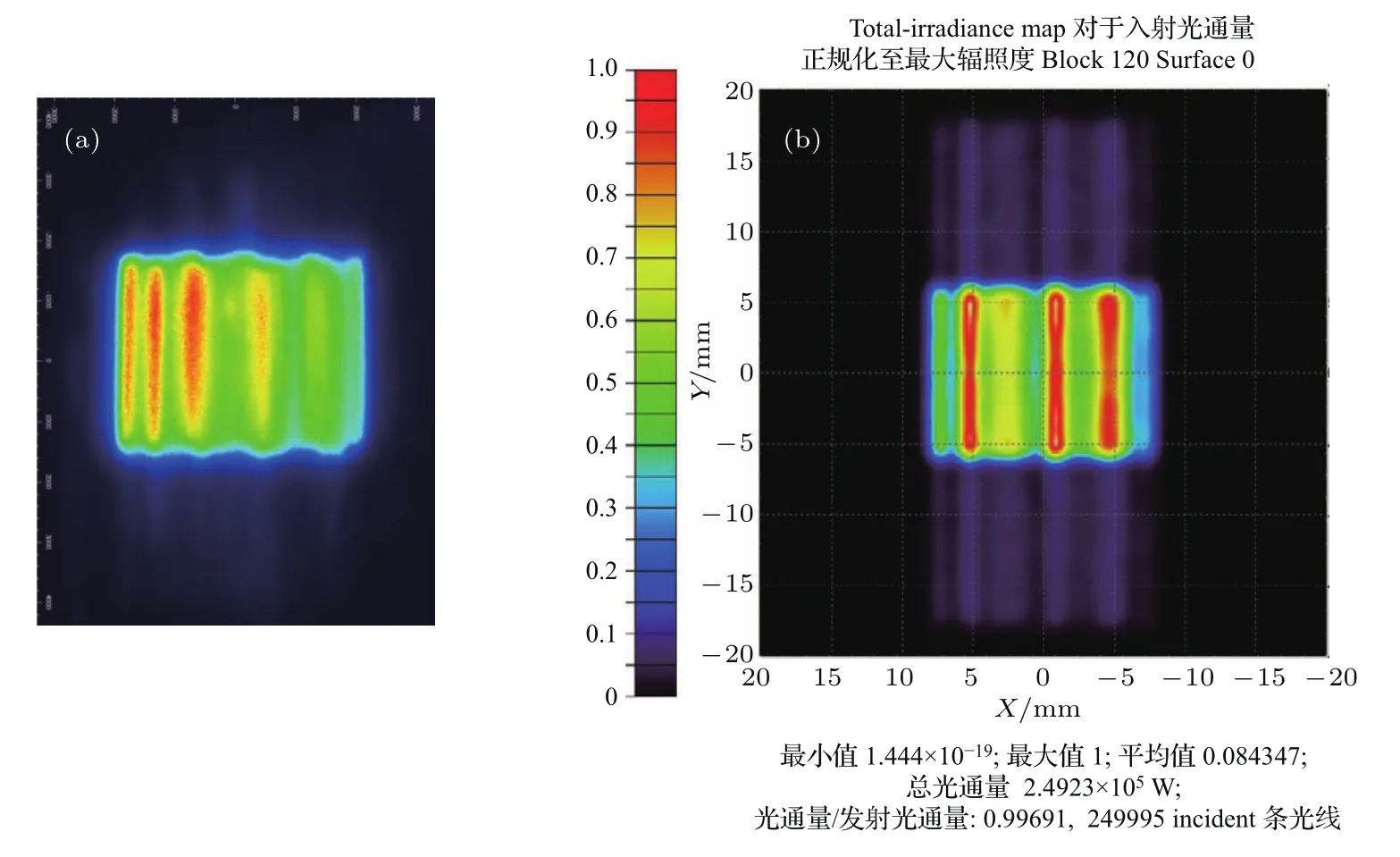
当h0 图3 非准直光入射成像型微透镜阵列匀束系统光线图[22]Fig.3.Scheme of imaging microlens array system with non-collimated beam[22]. 当h0>PLA/2,子光束入射到对应的第二子透镜孔径范围外,进入其他的子透镜孔径(如图3中θ2光线所示).对应子透镜孔径范围外的光线,其傅里叶透镜焦平面处的扩展光斑相对于入射角为θ1时位置发生了平移,并且与入射到对应子透镜孔径范围内的子光束的扩展光斑不相重合. 可见,当入射光束的发散角太大时,较大角度的光线不能与目标区域重合,在目标区域外形成旁瓣,造成抽运能量利用率的下降. 根据前面的分析,定义h0=PLA/2时,θ为微透镜阵列接收角,可得 当a12>f1且a12增加时,接收角θ会减小,对LD发散角容忍度降低;当a12减小时,接收角最大可达但抽运强度则会变小.所以在实际应用中,为兼顾抽运强度和接收角,通常选择a12=f1.此时,对于最大发散角已知为θ的确定光源,为保证不出现旁瓣,微透镜单元参数的设计应满足h0 光场的均匀性是评价匀束系统最为重要的指标,通常用不均匀度(U)进行度量,其定义为 其中Imax与Imin分别为光场的最大值与最小值. 对微透镜阵列匀束系统光源匀化机制的分析表明,像面光场匀化的思想基于初始光场的分割和多个子孔径光场在像面上的叠加.可以证明由多个子光场投影叠加形成的像面光场不均匀度必然小于等于单个子光场不均匀度的最大值. 将LA1各微透镜单元编号1到n,单元i划分的子光场强度分布记为Ii(xi,yi),xi与yi分别为以各微透镜子单元光轴位置为原点的二维坐标,则像面上的光场分布分别为以傅里叶透镜光轴位置为原点的二维坐标,为微透镜子单元口径到像面的扩束倍数的倒数. 如果每个微透镜单元孔径内的光场不均匀度都小于a,即Ii-min分别表示单元i划分的子光场的最大值与最小值.计算可得 将多个微透镜单元对应的不等式相加,可得 LD阵列抽运场不均匀度小于10%在实际应用中是一个可以接受的指标.根据上面的分析,如果我们设计时保证各个微透镜单元孔径内的光场不均匀度都小于10%,则必然可以保证微透镜阵列匀束系统像面上的光场不均匀度小于10%,从而满足抽运场不均匀度需求. 在微透镜阵列匀束系统的实际使用中,由于匀束系统光束接收角的要求,LD阵列需要对发散角较大的快轴(约40◦)进行准直.准直后的LD抽运光场不均匀度较大,存在小尺度尖峰(图4(a)).如果以此进行光束分割,为保证单个微透镜单元孔径内的光场不均匀度小于10%,则需要选择单元尺寸很小的微透镜阵列进行光场分割(约10µm级),以现有的微透镜阵列加工工艺很难实现. 图4 LD阵列抽运典型光场 (a)近距离传输;(b)远距离传输Fig.4.Typical pump field of LD array:(a)Short distance transmission;(b)long distance transmission. 通常采用的解决方法就是让微透镜阵列离开LD阵列足够的距离,使LD阵列的快轴光束充分发散并匀化(图4(b)),从而保证采用较大尺寸的微透镜单元时,孔径内的光场不均匀度小于10%,从而获得不均匀度小于10%的像面光场.但LD阵列的光束充分发散必然造成光场口径扩大,所以需要更大口径的微透镜阵列,同时微透镜阵列离开LD阵列距离较大,会造成抽运匀束系统结构复杂化. 另一种设计思想是,使各个微透镜单元口径内的子光场服从随机分布,则可以通过增加通光的微透镜单元数获得低不均匀度的叠加光场. 假设初始光场为Iin,其最大值和最小值分别为平均值(数学期望)为µ,方差为σ2,易知. 可以知道光场被LA1分割后微透镜单元i对应子光场强度且随机变量Ii(xi,yi)和Iin具有同样的数学期望E(Ii)=µ和方差D(Ii)=σ2.随机变量Ii的数量为LA1的通光单元数n. 而像面光场分布为各子光场的叠加: 根据随机变量序列的中心极限定理:随机变量的和的分布随变量数的增加趋于正态分布.像面光场分布I(x,y)为正态分布,且具有数学期望 由正态分布的3σ性质可知,在数学期望附近 3σ区间内的概率为>99.7%,也就是I几乎必然位于区间内. 可以认为像面上的光场分布不均匀度 而σ6(Iin-max−Iin-min)/2,可以得到微透镜阵列通光单元数计算公式: 测量输入抽运场的最大值Iin-max、最小值Iin-min和平均值µ,根据上述计算公式与输出光场不均匀度期望值U,可以获得匀束系统所需的微透镜阵列通光单元个数n. 上述分析成立的前提是各个微透镜单元孔径内的子光场服从随机分布.我们知道LD阵列的光束分布呈周期性排列,而微透镜阵列的单元也呈周期性排列,当微透镜阵列单元周期为LD阵列周期的整数倍时,各个微透镜单元口径内的子光场分布相似,叠加后像面光场分布与单个微透镜单元光分布仍然是相似的,并不能实现均匀化的目的.需要通过设计微透镜阵列的单元周期来规避这一问题. 我们开展了基于微透镜阵列匀束的LD面阵抽运设计与实验验证.设计与实验采用的LD面阵主要技术参数如表1所列,实测LD面阵自由传输发光场如图5所示. 图5 实测LD面阵自由传输发光场 (a)传输5 mm;(b)传输70 mm;(c)传输170 mmFig.5.Measured pump field of LD array:(a)The pump field transmits 5 mm;(b)the pump field transmits 70 mm;(c)the pump field transmits 170 mm. 表1 LD面阵主要技术参数Table 1.Parameters of LD array. 根据LD面阵发光场参数开展微透镜阵列参数设计:LD光线最大发散角为10◦,即光线最大偏移角为5◦,可得微透镜F数 为保证余量,取F数为4.根据图5(a)伪彩色图像灰度,对抽运场强度归一化,取Iin-max=1,Iin-min=0,µ=0.6,目标抽运场不均匀度U优于0.1,代入计算公式可得n>625,由抽运场尺寸即微透镜阵列通光面尺寸约20 mm×10 mm,可得微透镜单元面积小于0.32 mm2,根据抽运场需求设计微透镜单元形状为正方形,可得正方形边长小于0.56 mm,为便于加工同时避开bar条周期,设计边长为0.5 mm. 我们采用二维发散角分别为1◦与10◦,发光面尺寸为0.1 mm×10 mm的光源模拟准直后的LD面阵bar条,指向一致性采用均方根值1/3,平均值的随机数对快轴偏离角进行模拟(此处同样考虑正态分布的3σ原则,bar条装配时偏离角可认为呈正态分布,快轴偏离角度装配目标值为0,即数学期望为0,最大值为1,即3σ约为1,可假定均方根值为1/3),计算得到自由传输发光场如图6所示,与实测光场基本类似. 我们搭建了两套抽运耦合匀束系统开展对比实验,系统1使用的微透镜阵列参数不满足前文分析的设计条件,系统2中微透镜阵列采用了3.1节的设计参数;匀束系统具体参数见表2. 抽运耦合匀束系统耦合输出抽运场分别如图7和图8所示. 图6 仿真LD面阵自由传输发光场 (a)传输5 mm;(b)传输70 mm;(c)传输170 mmFig.6.Simulated pump field of LD array:(a)The pump field transmits 5 mm;(b)the pump field transmits 70 mm;(c)the pump field transmits 170 mm. 表2 微透镜阵列匀束对比实验系统参数Table 2.Parameters of microlens array in contrast experiment. 图7 抽运耦合匀束系统1耦合抽运场 (a)实测结果;(b)仿真结果Fig.7.Output pump field of pump coupling system 1:(a)Measured results;(b)simulated results. 图8 抽运耦合匀束系统2耦合抽运场 (a)实测结果;(b)仿真结果Fig.8.Output pump field of pump coupling system 2:(a)Measured results;(b)simulated results. 系统1的输出抽运场在慢轴方向均匀性较好,而快轴方向调制度较大,在慢轴方向上还存在明显旁瓣.分析原因,抽运光在微透镜阵列上约通过4×3个单元,通过微透镜单元数较少,无法达到匀束的效果;微透镜单元在快轴方向上F数为6,慢轴方向上F数为7.8,而所用的LD阵列,快轴光线最大偏离角度为1.5◦,慢轴光线最大偏离角度为5◦.计算可知,为保证耦合抽运场无旁瓣,快轴方向上F数应小于19.1,慢轴方向上F数应小于5.7.微透镜单元在快轴方向上F数满足要求,而慢轴方向F数较大,导致了慢轴方向的明显旁瓣. 系统2的输出抽运场快轴、慢轴均匀性均较好,实测不均匀度为7.9%,且无任何旁瓣.根据计算,抽运光在微透镜阵列上约通过40×20个单元,单元数足够多(∼800),且快慢轴F数为4,小于耦合无旁瓣条件,最终实现了较好的匀束效果.实验中LD面阵驱动电流200 A/1 ms,实测输出能量为4.50 J,透镜焦平面光斑尺寸约10 mm×10 mm,能量为4.08 J,系统耦合效率约90.7%,略小于模拟计算结果,主要由于短焦透镜曲率半径较小,大角度入射光线反射率高于预期所致. 对于我们关注的输出抽运场不均匀度这一重要指标,系统2比系统1表现出明显的优势,其原因在于两个方面.首先,系统2的微透镜单元面积(0.25 mm2)远小于系统1微透镜单元面积(37.8 mm2),在各个微透镜单元内的光场调制度也相应较小,最终形成的叠加光场调制度也会降低;其次,系统2单元数(∼800)远大于系统1单元数(12),根据前文理论分析,不均匀度与为通光单元数)呈正比,所以理论上系统2不均匀度约为系统1的1/8,实验结果也与理论计算较好地符合. 根据实验结果可见,只需要根据LD面阵光线发散角设计微透镜单元参数,根据匀束指标设计微透镜阵列通光单元数量,同时保证微透镜阵列与LD面阵的空间周期去相关,就可以实现较好的耦合匀束效果,同时微透镜匀束系统通过优化元件可以实现很高的耦合效率. 本文分析了基于成像型微透镜阵列匀束的LD面阵抽运耦合系统,采用几何光学和数理统计分析的方法开展理论研究,明确了微透镜阵列的各项参数(微透镜单元的形状、尺寸、焦距、阵列通光单元数等)设计的边界条件,并通过实验进行验证,为微透镜阵列在LD面阵抽运耦合系统的实际应用提供了依据.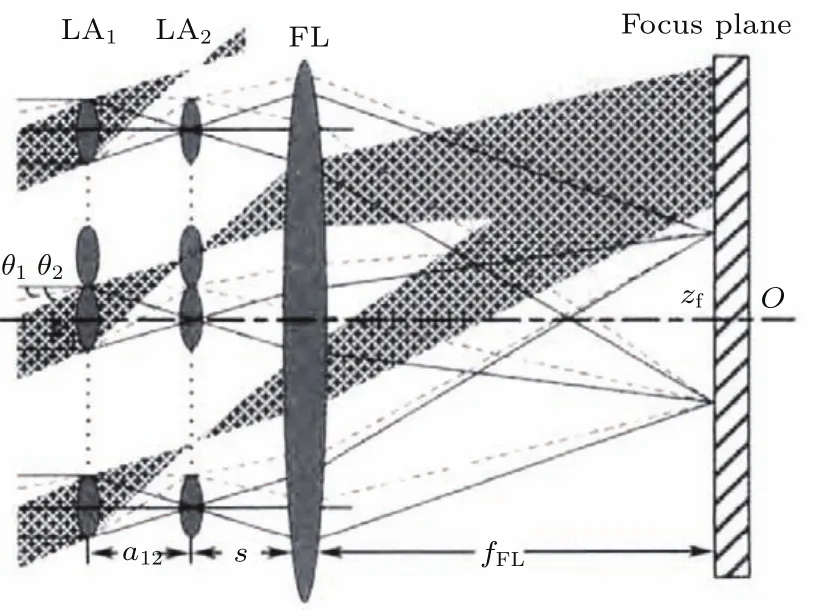

2.3 阵列通光单元数
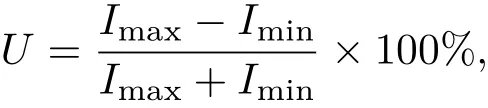



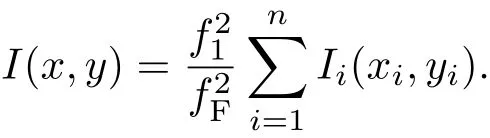
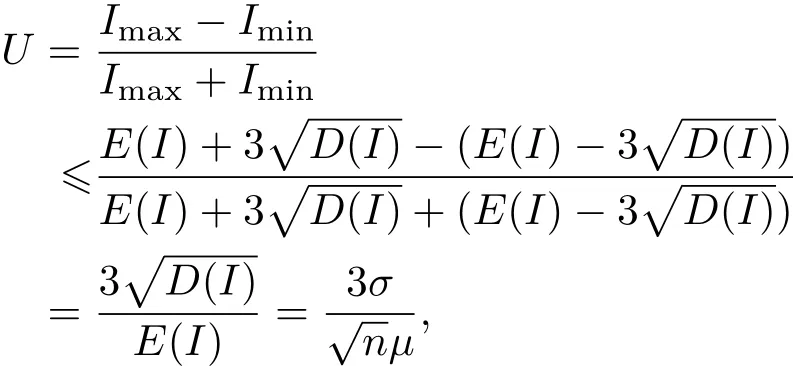
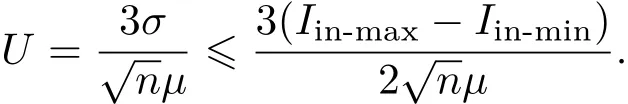
3 抽运耦合匀束系统设计与实验验证
3.1 匀束系统参数设计


3.2 匀束系统仿真与对比实验测试


4 结 论

