基于小波变换的提高激光引信测距精度研究

路 明,孔德浩,苏益德

(1.海军航空大学,山东 烟台 264001；2.中国人民解放军92916部队,海南 三亚 572000)

1 引 言

激光引信是一种利用激光原理在预定距离探测目标,并在最佳炸点位置处引爆战斗部的近炸引信。激光引信的探测脉冲窄、调制方便,能够精确探测目标距离和位置,具有引战配合效率高和抗电磁干扰能力突出等优点,特别适应现代战争精确打击和光电对抗技术的发展[1]。随着军事领域技术的不断发展,激光引信的测距精度要求也不断提高,本文主要探讨脉冲体制激光引信的测距精度问题。

脉冲激光引信按测距信息获取方式分为模拟激光引信和数字激光引信,目前比较常用的模拟激光引信信号处理算法是前沿鉴别法(也称固定阈值法),数字激光引信信号处理算法是恒定比值鉴别法,此外还有峰值检测法、数字互相关法等[2]。本文在建立脉冲激光引信发射信号与回波信号模型的基础上,对比分析了前沿鉴别法、恒定比值法和峰值检测法测距精度的优缺点,进而提出了一种基于小波变换的模极大值法来提高脉冲激光引信的测距精度。

2 脉冲激光引信测距原理

脉冲激光引信的测距原理与激光测距原理相同,当一个激光脉冲从激光引信的发射器出射时,记录此时刻为t1。随后,该脉冲经目标表面反射后形成回波,回波进入接收器时,再次记录此时时刻为t2,即可测得激光引信与目标间距为:

(1)

式中,c为真空中光速；(t2-t1)称为飞行间隔时间。

从式(1)中能够得知,确定距离L精确度的关键在于两点:①发射与接收时刻的确定；②飞行间隔时间的确定。在因素①中,发射/接收时刻的确定是指,在选取发射/接收时刻t1、t2时需确定发射脉冲信号与经目标反射的回波信号上与之对应的时刻点。下文中分析的激光引信算法皆是针对因素①所讨论的,针对因素②,早已有一系列提高精度的测量方法,如数字法[3]、模拟法[4]和延迟线插入法[5],统称为时间间隔测量方法,故在本文中不做讨论。图1示意了脉冲激光引信测距原理。

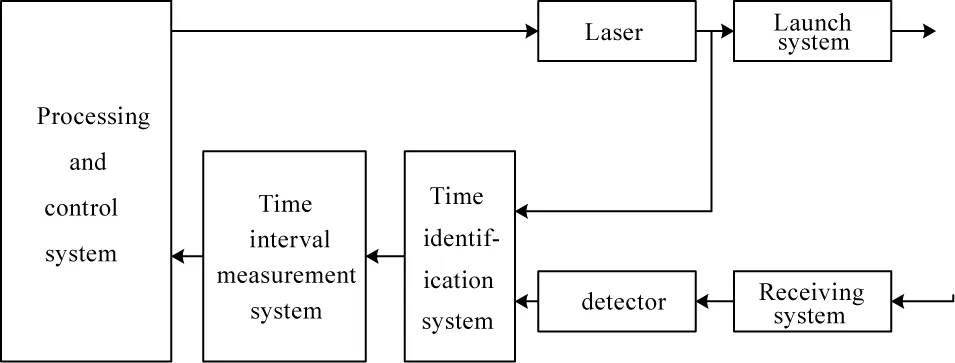
图1 脉冲激光引信测距原理图Fig.1 Pulse laser fuze ranging principle diagram

3 脉冲激光引信信号处理算法

3.1 前沿鉴别法

前沿鉴别法(又称固定阈值法)是指在确定起止时刻时采用将信号阈值进行固定的方式(如图2所示),即以脉冲信号上升沿中幅度达到固定阈值点所对应的时刻作为起止时刻。设发射脉冲信号幅度为V1,回波脉冲信号幅度为V2,固定阈值幅度为Vτ,记V1上升沿达到Vτ时所对应的时刻为t1,V2上升沿达到Vτ时所对应的时刻为t2,则起止时刻对应的时间间隔T=t2-t1即为目标回波信号与发射脉冲的延迟时间,从而可计算出引信与目标间的距离。

然而,不难看出前沿鉴别法具有以下两个明显的缺点:一是阈值的选择,难以选择能够令漏警和虚警概率都低到满足要求的合适阈值；二是对于不同目标,即使在相同间距时其回波信号强度也相差很大,这就使得产生漂移误差Δt(见图2),这一误差由信号幅度与形状的变化导致,其大小同样与所选取的阈值有关。因此,前沿鉴别法是存在较大测量误差的,而且前沿鉴别法非常依赖于接收系统的信噪比,仅适用于信噪比较高(S/N>5)的情况。

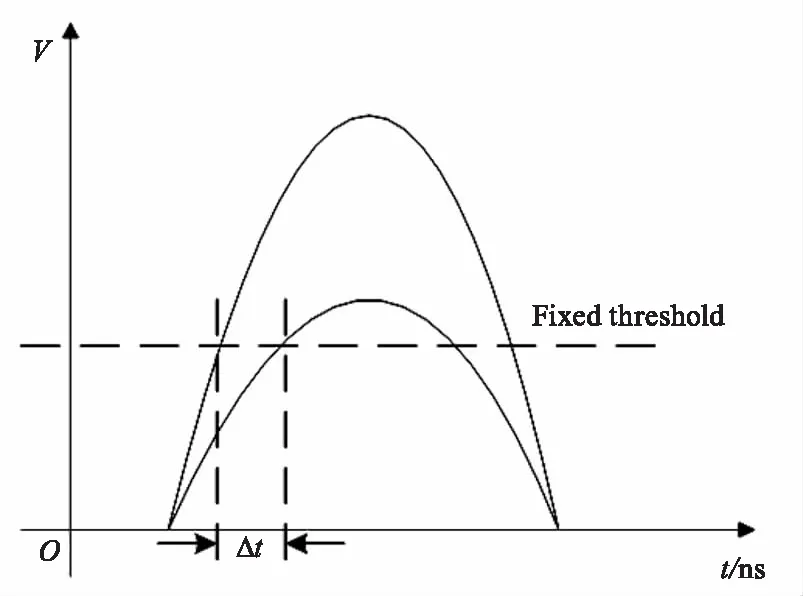
图2 前沿鉴别法示意图Fig.2 Frontier identification method diagram

3.2 恒定比值鉴别法

为了提高激光引信的测距精度,恒定比值鉴别法在发射脉冲与回波信号中选取定时比例点来进行计算。这是由于信号在波形形状不变的情况下,其脉冲前沿幅度上升相同比例所对应的时间不变。同时在选取定时比例点时要考虑波形的形状,通常选取脉冲前沿上斜率最大即变化率最高的点作为定时比例点,从而得到较高的测距精度。

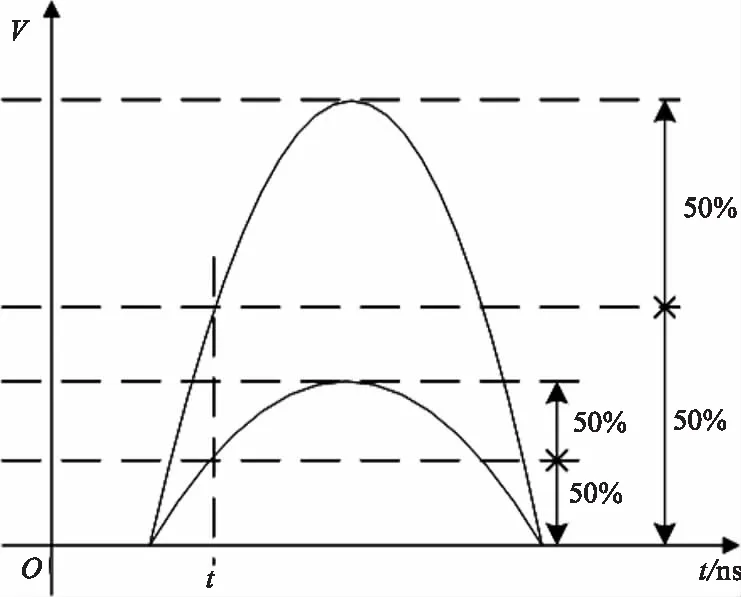
图3 恒定比值鉴别法示意图Fig.3 Constant ratio identification method diagram

图3示意了恒定比值鉴别法的图解原理,这里将比例取为50%,即选取脉冲前沿极值点的一半所对应的时刻作为起止时刻。设发射脉冲信号幅度最大值为V1,回波脉冲信号幅度最大值为V2,记发射脉冲上升沿达到V1/2时所对应的时刻为t1,回波脉冲上升沿达到V2/2时所对应的时刻为t2,则起止时刻对应的时间间隔T=t2-t1。在忽略波形不规则变化等一些因素影响的情况下,单纯由波形幅值变化而引起起止时刻的误差将会变小。根据原理可知,恒定比值鉴别法要优于前沿鉴别法。

3.3 峰值检测法

峰值检测法则是取脉冲的峰值点所对应的时刻为起止时刻,从而计算出目标距离。此方法的关键点在于峰值的检测,以典型的高斯脉冲信号为例,其重要参数有峰高H,峰宽W,半峰宽FWHM,标准差σ等,在标准高斯型中有关系如下:

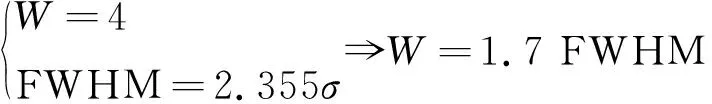
(2)

又根据Nyquist采样定理可知采样频率Fs应不小于信号中出现的最高频率Fmax的两倍,因此可得出一个脉冲宽度的总采样点个数为:

(3)

则在检测脉冲峰值时,首先记录初始值点,之后进入脉冲周期内,当采样值处于上升阶段,不断更新最大值的数据,直到采样值达到最大值并保持；当采样值进入下降段后,不再更新最大值,从而完成一个峰值检测周期。

图4展示了峰值检测法的原理,其中t1和t2分别是发射脉冲与回波脉冲峰值点所对应的起止时刻。

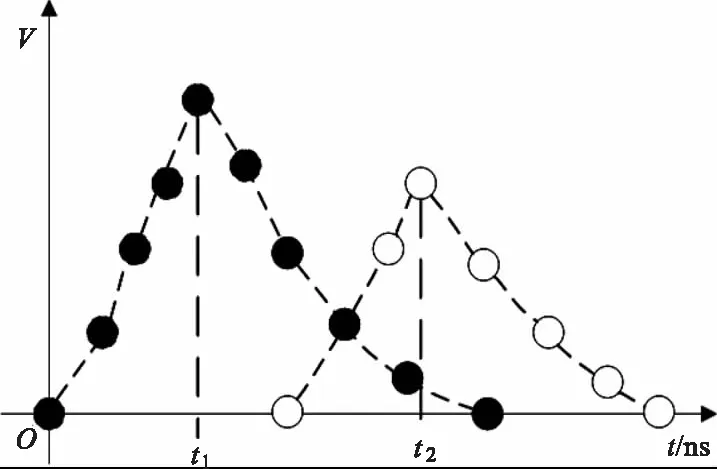
图4 峰值检测法示意图Fig.4 Peak detection method diagram

3.4 小波变换模极大值法

首先需要指出的是,回波波形上的孤立奇异点是天然存在的[6]。在忽略噪声信号与激光收发过程中由空气中杂质引起后向散射的条件下,引信的回波信号由幅值近似常数的环境噪声与环境噪声再叠加在发射激光脉冲经目标反射后的回波之上而组成的。于是,根据奇异点的特性可推断在引信回波信号中,从信号幅值为常数的环境噪声至出现回波脉冲信号的交界点处即为一个奇异点,在下文的仿真结果中也证明出该点的确为一个奇异点。

本文所研究的小波变换模极大值法,则是基于对回波信号进行小波变换后,信号中的孤立奇异点能被检测出来的基础上而提出来的。理论与下文的仿真结果都表明,在一定的小尺度下,小波变换后的模极大值点所在位置与回波信号中的孤立奇异点所处位置是相对应的[7]。基于上述原理,本文采用求出回波信号经小波变换后的模极大值点所在位置,从而获得相对应的回波信号上孤立奇异点所处的位置。于是,我们可以确定起止时刻(即式(1)中t1和t2)即为发射脉冲的发射时刻与回波波形上的孤立奇异点所对应的时刻,通过对引信回波信号作二进离散小波变换,得到变换后信号的模极大值点的位置来得到对应的t2时刻值,从而完成测距。

4 目标回波特性模型建立

4.1 发射激光脉冲模型

发射激光脉冲模型通常可被看作是时间与空间两部分间的乘积,其中时间的部分即为脉冲调制函数,其在文中取为[8]:

(4)

式中,PM0为发射脉冲的功率；τ为脉冲的半峰值脉宽的计量单位,这里取6 ns。参数n决定脉冲波形的形状,一般取n=2时所对应的窄脉宽且对称的理想脉冲信号,脉冲宽度为Tp=1.22×τ。

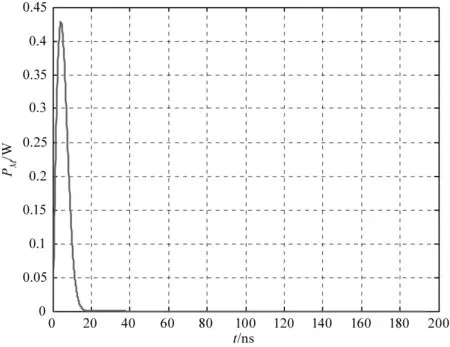
图5 激光发射脉冲波形图Fig.5 Laser emission pulse waveform

图5为n=2时的Matlab仿真出的发射脉冲信号图。

在本文中,我们认为发射激光束是一束基模厄米—高斯光束,则其光强在空间的分布符合高斯型公式[9]:

(5)

式中,λ为发射激光波长;w0为发射激光的腰斑半径。光强I(x,y,z)十分值得关注的一点是其物理意义为光在单位面积上的功率。下文用pt来表示发射激光脉冲处于t′时刻时光在单位面积上的功率,进而由式(4)和式(5),可以推出pt表达式为:

(6)

4.2 回波脉冲功率模型

目标的材质不同,其对激光的反射程度也不同,本文选择推导朗伯体[10]这种理想目标情况下的回波功率表达式。建立如图6所示方便描述的坐标系,以引信所在位置为原点,Γ面为发射激光脉冲的边界面,OA与OB为Γ面与ZOY面的交线,OA与OZ夹角为脉冲激光束的半发散角α,则Γ面的方程可表示为:

(7)

图6 方便描述的坐标系Fig.6 Convenient description of the coordinate system

在目标表面上取一点(x,y,z)为原点建立与上述相同的坐标系,则其Z轴正向与点(x,y,z)的外法线方向一致。对于朗伯体而言于是有:

I=kcosθ

(8)

式中,I为辐射强度;θ为激光经反射回引信方向与Z轴的夹角;k为比例常数。现将体统中的能量损耗忽略,假设发射脉冲激光至目标表面位于点(x,y,z)附近,那么该发射脉冲激光在单位面积上的功率则为pt。又因前文设定将目标视为理想朗伯体表面,照射在点(x,y,z)附近处面积为ΔS范围内的激光功率将被完全反射进大小为2π立体角内,进而可知:

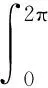
(9)

式中,等式左侧为发射激光脉冲照射到点(x,y,z)附近处面积为ΔS范围内的入射总功率,右侧为经目标表面反射后的出射总功率。将式(8)代入式(9)中,可得:

(10)

将式(10)代入式(8)得:

(11)

设激光接收器位置与点(x,y,z)所连直线同此点的外法线相夹A角,Ar为接收器上有效接收面积,接收器与点(x,y,z)相距r,从而可获得引信接收器接收到的功率表达式为:

(12)

进而考虑各种损耗后,接收器在t时刻接收到的回波功率表达式为:

(13)

式中,Σ为目标表面被激光照射到的区域；pt(t′,x,y,z)从式(6)表示；τr,τt,τa皆表示系统的光学透过率,其分别为接收透过率、发射透过率与大气透过率；ρ表示目标表面反射率。

同时,式(13)中t′与时刻t满足如下关系式:

(14)

式中,r表示引信与点(x,y,z)的间距;c为光在真空中的传播速度。记Σ在XOY面上的区域投影为Dxy,可将式(13)写作:

(15)

式中,加上绝对值是因为被积函数代表单位面积上的功率,不能出现负值的情况。现再设目标表面方程为F(x,y,z)=0,则有:

(16)

(17)

将式(16)和式(17)代入式(15)可得:

(18)

目标表面方程又可表达为z=f(x,y),故有:

(19)

将式(19)代入式(18),可得到引信在t时刻所接收到的回波功率表达式为:

|xfx+yfy-z|·dxdy

(20)

4.3 目标回波波形仿真

为了较好地比较各个算法之间的效果,保证回波信号的稳定,本文选取平面目标进行回波波形仿真。这里假设平面目标平行于X轴且与Z轴相交于点(0,0,z0)(z0>0),其方程可表示为:

ycosβ+(z-z0)sinβ=0

(21)

即:

z=z0-ycotβ

(22)

图7示意了平面目标与激光引信间的相互位置关系。图中Σ面表示目标平面,其垂直于ZOY面,且交ZOY面于线EF,交Z轴于点D(0,0,z0)；Σ面法线OC与OY夹角为式(21)中的β；圆锥面Γ与图6中一样,其方程仍旧由式(7)确定,Σ面方程由式(20)表达。那么在实际仿真时,只需用式(22)表示目标表面方程就可以了。

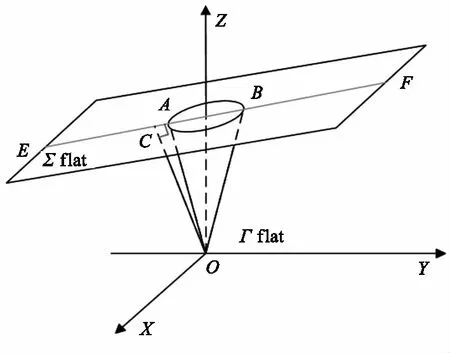
图7 平面目标在坐标系中的位置图Fig.7 Plane target position map in the coordinate system

从式(22)中可以看出,决定目标状态的两个参数就是zo和β。图8、9、10分别展示了仿真得到的回波波形。

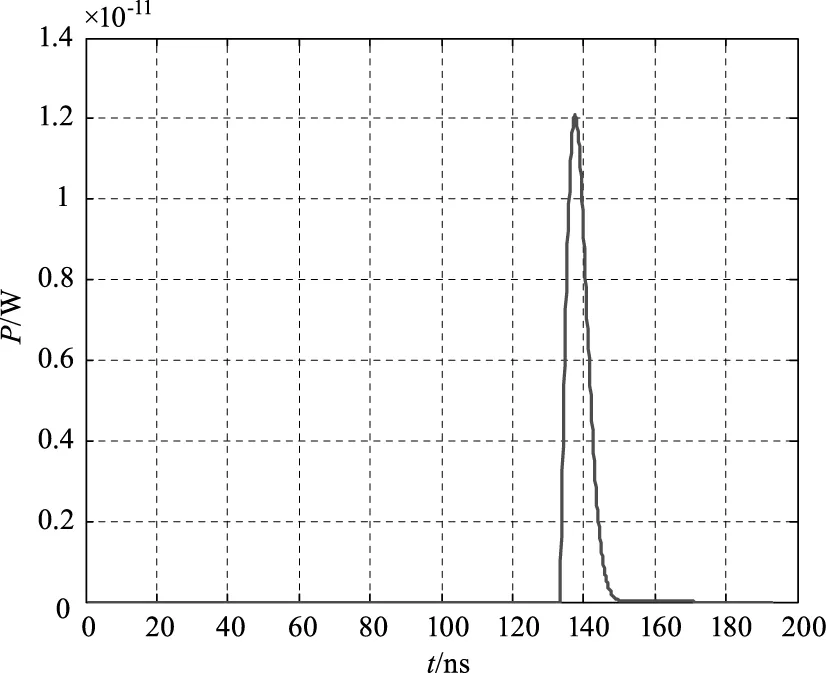
图8 取zo=20 m,β=π/2时,无噪声干扰下的回波波形Fig.8 When zo=20 m,β=π/2,echo-free waveform without noise

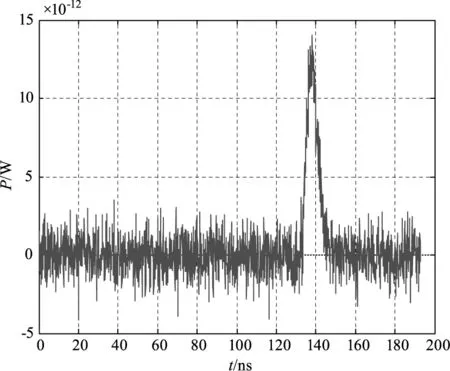
图9 相同条件下,在信噪比为5的高斯白噪声干扰下的回波波形Fig.9 Under the same conditions,the echo waveform under the interference of Gaussian white noise with signal to noise ratio of 5

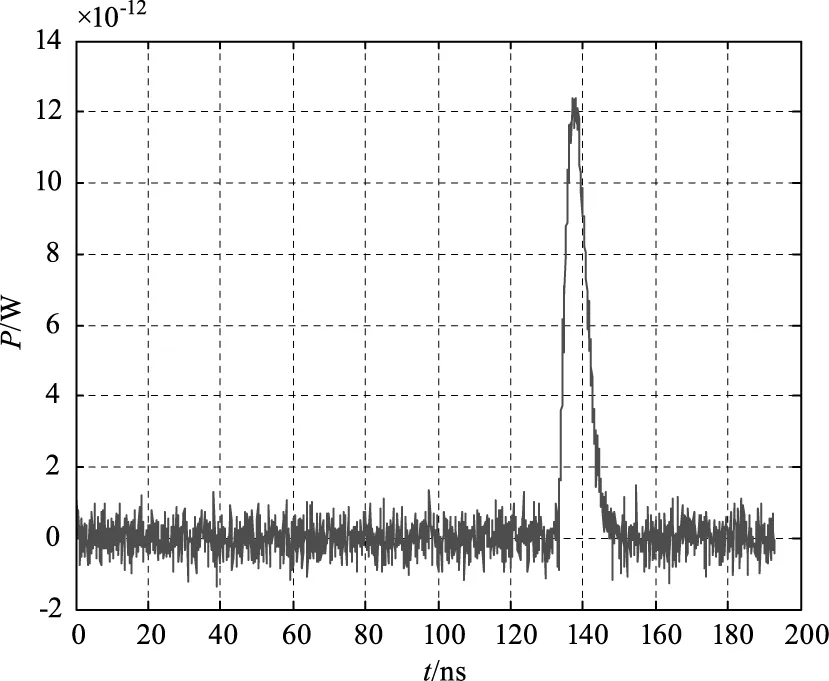
图10 相同条件下,在信噪比为13的高斯白噪声干扰下的回波波形Fig.10 Under the same conditions,the echo waveform under the interference of Gaussian white noise with signal to noise ratio of 13

5 算法仿真与分析

5.1 传统算法的仿真

为比较前文所述的前沿鉴别法、恒定比值鉴别法和峰值检测法测距效果之间的异同,对图9和图10所示加噪后的回波进行测距。对每种方法都分别进行了100次测距并与真实距离20 m进行比较从而计算测距误差。

5.1.1 前沿鉴别法

图11和图12分别展示了信噪比SNR=5和SNR=13时测距次数在测距误差区间上的分布情况。

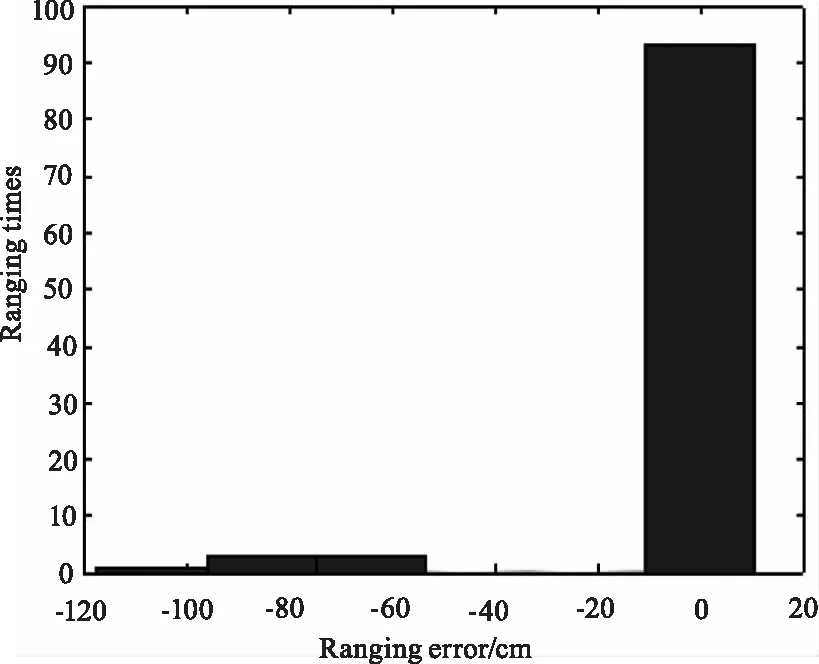
图11 SNR=5时,前沿鉴别法的误差直方图Fig.11 When SNR=5, the error histogram of the forefront of identification

5.1.2 恒定比值鉴别法

图13和图14分别展示了信噪比SNR=5和SNR=13时测距次数在测距误差区间上的分布情况。

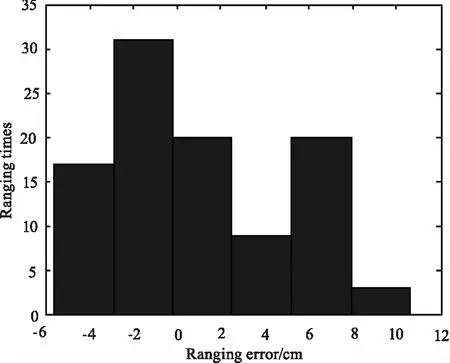
图12 SNR=13时,前沿鉴别法的误差直方图Fig.12 When SNR=13,the error histogram of the forefront of identification

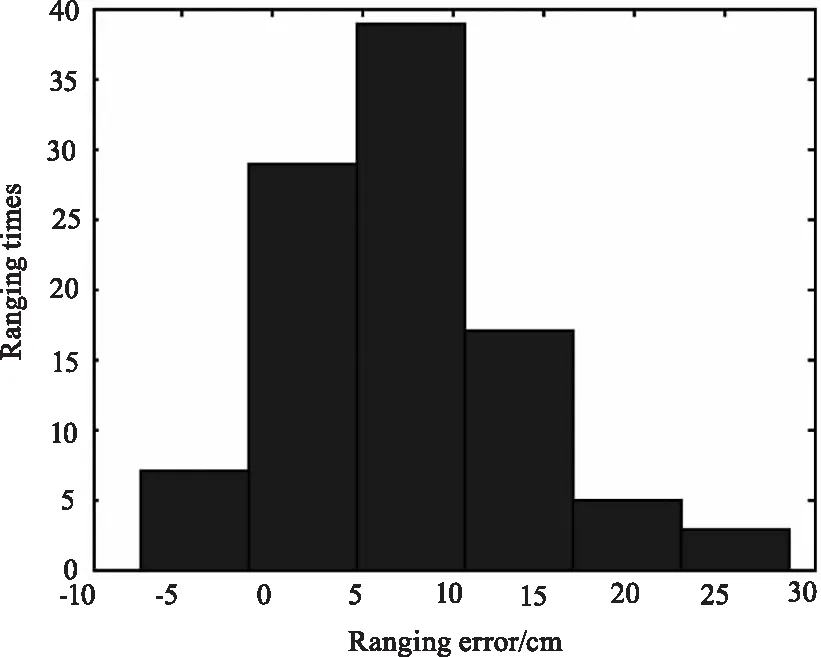
图13 SNR=5时,恒定比值鉴别法的误差直方图Fig.13 When SNR=5,the error histogram of the constant ratio identification method

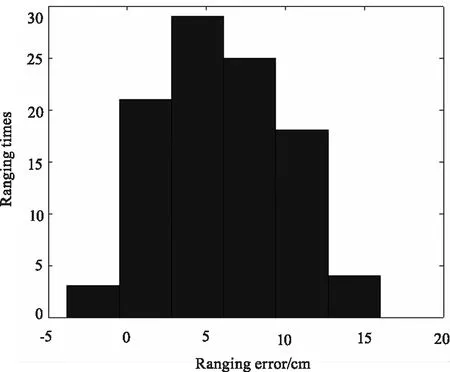
图14 SNR=13时,恒定比值鉴别法的误差直方图Fig.14 When SNR=13,the error histogram of the constant ratio identification method

5.1.3 峰值检测法

图15和图16分别展示了信噪比SNR=5和SNR=13时测距次数在测距误差区间上的分布情况。

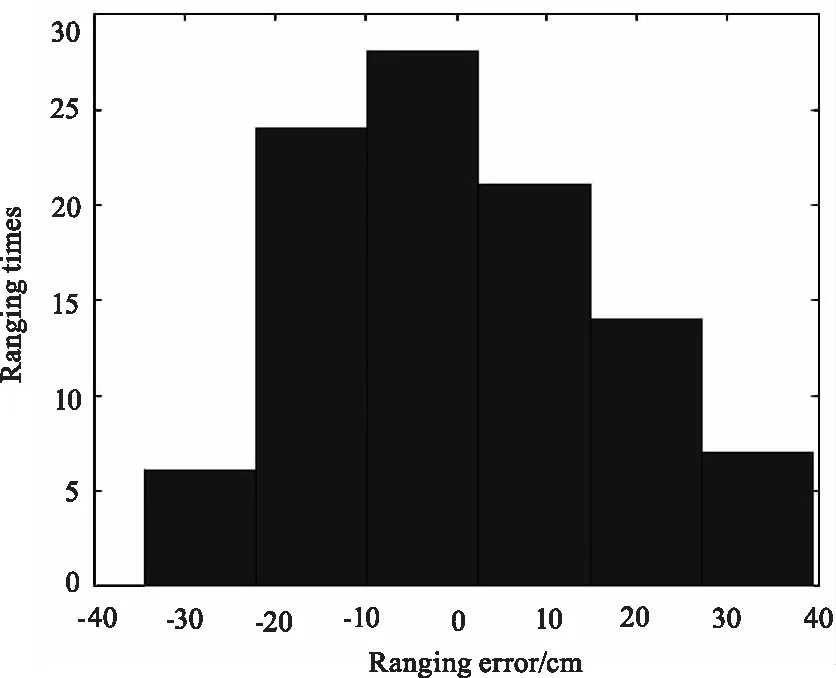
图15 SNR=5时,峰值检测法的误差直方图Fig.15 When SNR=5,the error histogram of peak detection method

5.2 小波变换法的仿真

图17展示了信噪比SNR=13回波信号的小波变换五层细节的模值图,由图中可以看出来从第三层开始就能够看出模极大值及其所对应的时刻点。

经过计算发现,选取第四层细节进行计算结果最为精确。同样地,图18和图19分别展示了信噪比SNR=5和SNR=13时,采用小波变换法测距次数在测距误差区间上的分布情况。

5.3 四种算法测距误差分析

比较上述四种算法仿真出误差直方图可以明显看出,前沿鉴别法在信噪比SNR=5时误差最大即最易受到噪声影响,从而验证了其仅适用于信噪比较高的特点；而峰值检测法受信噪比的影响并不大但是此方法整体的测距误差较大,精度不高,在高信噪比情况下不如前沿鉴别法；相比之下恒定比值鉴别法要优于前两种方法,其测距精度受信噪比的影响不大且在前三种传统方法中误差最小,这也是目前大多数激光引信所采用的算法；小波变换的模极大值算法,在本文所仿真的条件下测距效果明显优于其他三种传统算法,其受信噪比影响较小,误差范围分布也较小,在高信噪比条件下可将测距误差控制在厘米量级,可作为一种较为理想的算法。

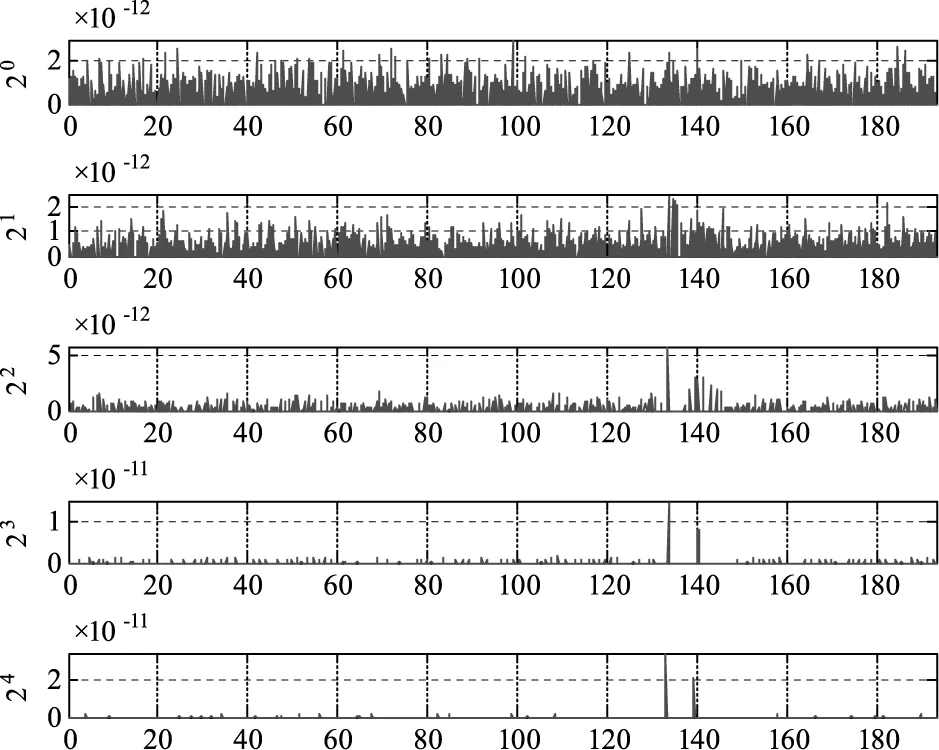
图17 信噪比SNR=13回波信号的小波变换五层细节模值图Fig.17 Signal to noise ratio of 13 echo signal wavelet transform five layers of detail modulus diagram

图18 SNR=5时,小波变换法的误差直方图Fig.18 When SNR=5,the error histogram of wavelet transform method

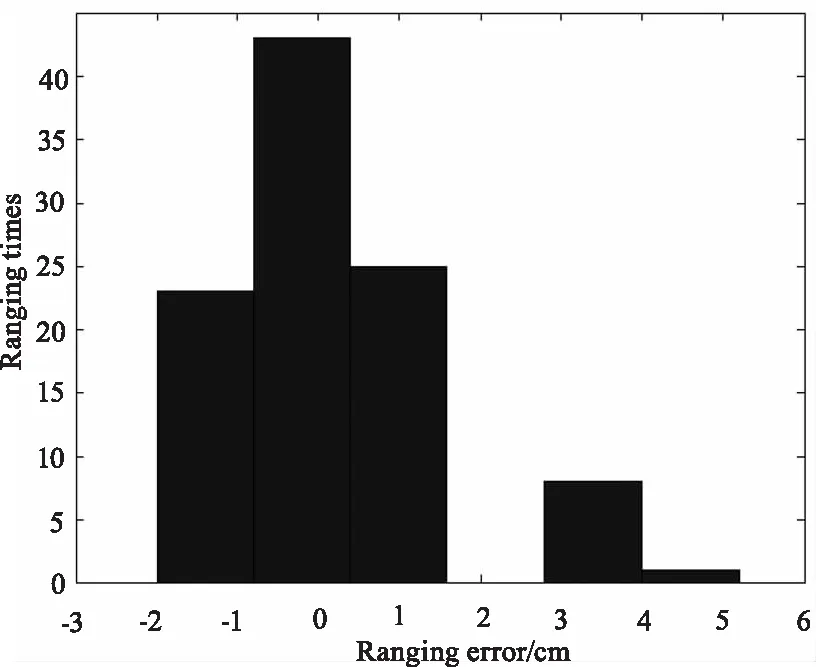
图19 SNR=13时,小波变换法的误差直方图Fig.19 When SNR=13,the error histogram of wavelet transform method

6 结 论

测距精度是衡量激光引信性能的关键指标。本文在研究激光引信传统测距算法的基础上提出了一种对回波信号进行小波变换后求其模极大值所对应的时刻点从而完成测距的方法。

通过对目标回波信号进行建模并使用Matlab软件将三种方法与小波变换法进行测距误差仿真,结果表明:三种传统算法中,前沿鉴别法的测距精度受信噪比影响大,峰值检测法测距误差范围较大,恒定比值鉴别法相对效果较好且为目前最常用的方法。本文所提出的小波变换法测距精度优于传统方法,受信噪比影响小,误差范围小,在高信噪比条件下可将误差控制在厘米量级,该方法为后续激光引信的研究工作提供了一定的理论和技术支持。