非相干多普勒测风激光雷达鉴频算法
刘延文,孙学金,张传亮,李绍辉
(国防科技大学气象海洋学院,江苏 南京 211101)
1 引 言
风对于大气能量循环、污染物扩散、水汽和气溶胶粒子的输送都有重要的影响,更是大气环流的根本动力,是数值天气预报和气候研究中最迫切需要的数据,并且局地风场在飞机起飞与着陆、火箭发射及军事等方面具具有重要的意义[1-4],但在当前全球观测系统中,对风的观测并不充分,和气压、温度、湿度等大气基本变量相比,风的观测较为薄弱[5]。当今世界气象组织主要通过无线电探空网、机载仪器和气象雷达来对风场进行探测,但无线电探空网分布不均匀,在南半球和洋面上观测数据有限[6],边界层以上的风速可以根据地转理论和气压测量值计算得到[8],但该方法只适用于中高纬地区,所以需要直接探测资料来对大气流动有更准确的认识。激光雷达作为近几十年来快速发展的探测仪器,被用于温度[8-9]、气溶胶浓度和光学厚度[10]的测量,对风场的测量也有时空分辨率和探测精度高、探测范围大、响应速度快的优点,星载激光雷达更是可以获得高精度的全球风场。多普勒测风激光雷达通过测量随风场运动的分子和气溶胶粒子对激光造成的多普勒频移来实现风场的测量,分子和气溶胶的后向散射光被激光雷达接收,通过干涉仪后光子被电荷耦合器(CCD)接收,利用CCD上光子的累积和分布计算得到多普勒频移,利用多普勒频移就可以得到风速,所以多普勒频移的计算精度决定了风速测量精度。对于边缘技术和条纹成像技术,都有多种多普勒频移的检测算法,尤其对于条纹成像技术而言,不同算法的计算精度、计算速度和计算稳定性都不同,所以需要根据不同的要求选择不同的算法计算多普勒频移。本文总结了非相干测风激光雷达的不同算法,介绍个各种算法的适用性,比较了不同算法的精度和误差。
2 多普勒测风激光雷达的探测原理
多普勒测风激光雷达发射激光脉冲并接收大气后向散射信号,大气分子和气溶胶粒子随风场运动会与激光产生多普勒效应,从而改变散射回波的频率,通过测量和计算得到多普勒频移,就可以计算出径向风速,其表达式为:
vd=2vLOS/λ
(1)
式中,vd为多普勒频移;vLOS为径向风速;λ为波长。从式(1)可以看出,多普勒频移与目标物的运动速度及激光雷达的工作波长有关,当激光雷达的载荷确定后,多普勒频移只与目标(分子或气溶胶)的运动速度有关。根据径向风速和激光的天顶角(地基)或天底角(空基和天基)便可计算出水平径向风速,其表达式为:
vHLOS=vLOS/sinθ
(2)
其中,vHLOS为水平径向速度;θ为天顶角或天底角。
3 激光雷达的鉴频方法
按照鉴频方式不同,测风激光雷达可以分为非相干激光雷达[11-13]和相干激光雷达[14-15]。相干技术首先利用光电二极管将光信号转化为电信号[16],然后出射信号与回波信号混频,拍频信号的频率就是回波信号的多普勒频移,主要用于大气中低层Mie散射回波信号的频移测量[17];非相干技术利用光学鉴频器将频移转化为功率、强度或功率空间分布变化,通过测量功率、强度或功率空间分布的变化来反演风速[18],探测范围可到大气中高层。
相干雷达的探测灵敏度、探测精度及信噪比高[19],噪声功率小,对太阳背景光不敏感[20],但对光学准直性要求高,接收视场角的失配会严重影响激光雷达的性能,对于短波长的多普勒激光雷达校准要求更为严格,且无法准确探测Rayleigh散射信号。非相干探测对光学系统和激光性能的要求相对较低,系统结构简单,技术成熟且容易实现,采用多脉冲累积可以提高信噪比和探测精度,减小激光散斑的影响,对Rayleigh散射和Mie散射信号都可以进行探测,利用短波长的激光可以提高Rayleigh散射强度,在气溶胶浓度为零的情况下也可以工作[21]。
非相干探测包括边缘技术和条纹成像技术。边缘技术是利用滤波器将后向散射回波信号的频移转化为能量变化,通过测量能量变化计算多普勒频移;条纹技术则是利用不同波长的光透过干涉仪后干涉条纹位置不同的原理来实现多普勒频移的测量,可采用的干涉仪有F-P标准具和Fizeau干涉仪等。F-P标准具的干涉条纹呈环状,且条纹的粗细和间隔不一致,风速与条纹半径变化为非线性关系[22],需要阵列式探测器动态追踪条纹变化,和线形像素探测器CCD不匹配,不利于测量[23-24],利用环状阴极倍增管可以解决此问题,但其量子效率较低[25],另一种解决方法是将环形条纹转变为线条纹,再用CCD探测[26]。Fizeau干涉仪的干涉条纹呈线形,可以直接通过CCD检测条纹重心的变化来实现多普勒频移的测量[23],这种鉴频系统光路简单,系统效率高,干涉仪口径要求低[27]。条纹技术一般用于测量Mie散射信号,而边缘技术对Rayleigh散射信号和Mie散射信号都可以测量,在敏感性上两种方法并没有显著的不同[21],风速测量精度十分接近[28]。
3.1 边缘技术
边缘技术可利用F-P标准具、M-Z干涉仪[29-31]、Michelson干涉仪、光栅、各种原子和分子滤波器[32],如钠、钾、碘[33]、银蒸汽滤波器等,探测灵敏度依赖于分子与气溶胶的后向散射率及风速大小,F-P标准具是非相干探测的主要鉴频器[34-37],其透过率曲线具有陡峭的边缘,入射光频率变化会使透射光的的强度发生明显变化。
3.1.1 单边缘技术
由于标准具透过率曲线半宽点对应频率处的斜率最大,所以出射激光的频率υE锁定在此处,微小的频移将使标准具的透过率发生明显变化。由于布朗运动,Rayleigh散射和Mie散射光谱的谱宽有很大差别,但都可用高斯函数来表示:
(3)
式中,σx为散射信号光谱的标准差,下标“x”表示不同散射类型,“R”表示Rayleigh散射,“M”表示Mie散射。分子散射光谱的标准差σR=(8kT/mλ2)1/2;Mie散射谱线宽度表示为σM=συ0/(8ln2)1/2,συ0为发射激光的谱宽。通过标准具的光是入射光光谱和标准具透过率曲线h(v)的卷积,表示为:
T(υ)=fx(υ)*h(υ)
(4)
其中,“*”表示卷积,所以透过干涉仪的能量为:
I(υ)=I0·T(υ)
(5)
其中,I0为入射光的光强。
标准具的频率灵敏度的定义为:单位频率变化造成透过率的相对变化,表达式为:
(6)
根据多普勒频移和速度之间的关系:υd=2v/λ,标准具的速度灵敏度(单位速度变化引起标准具透过率的相对变化)表达式为:
(7)
则径向速度为:
(8)
式中,II′为回波信号的强度;II为回波信号通过标准具后的强度;IE′为发射激光的光强;IE为出射激光透过标准具的强度。
3.1.2 双边缘技术
双边缘技术是单边缘技术的改进,其测量灵敏度和精度比单边缘技术都要高[37]。标准具中心以一定间隔分开,得到两个分辨率、精度、频谱分布相同,但峰值透过率对应频率不相同的两个通道,出射激光频率锁定在两个透射率曲线的交叉位置,回波信号通过标准具两个通道的能量随频率变化,利用两个通道上接收到的能量,便可以计算出回波信号的频移,其测量原理如图1所示。
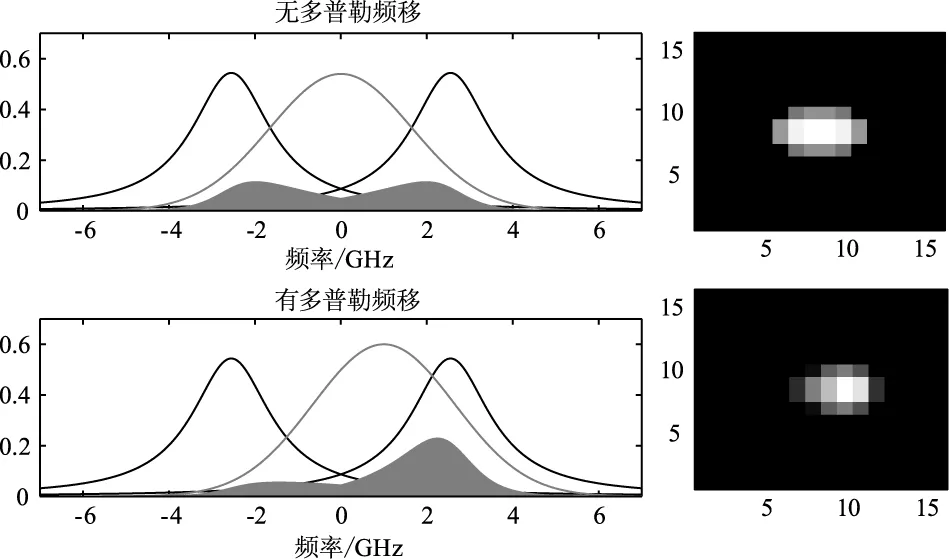
图1 基于F-P标准具的Rayleigh散射多普勒测量原理及CCD成像Fig.1 Rayleigh scattering doppler measurement principle based on F-P interferometer and CCD imaging
双边缘技术包括连续双通道技术和离散双通道技术,两种技术原理相同,只是回波信号在探测器内的路径不同,离散双通道技术是利用分光片将回波信号平均分为两束[38],然后分别通过标准具的两个通道,当风速为零时,两个通道上接收到的能量相等,当径向风速不为零时,回波信号频率改变,透过两个通道的的能量不相等,利用两个标准具透过的能量便可计算出频移,其离散双边缘透过率如图2所示。
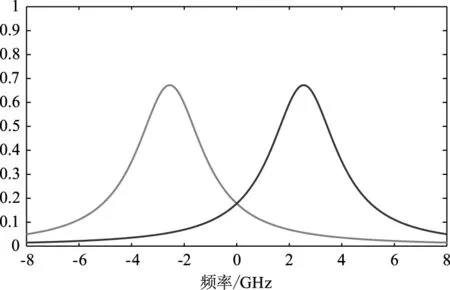
图2 离散双边缘透过率Fig.2 Discrete double-edge transmittance
连续双通道技术不再将大回波信号分离,而是直接进入一个通道,该通道的反射信号进入另一个通道,如图3所示,假设通道A和通道B的透过率都为10%,回波信号首先进入通道A,10%的光子透过通道A,90%的光子被反射进入通道B,则通过通道B的光子数仅占总光字数的9%(90%×10%),虽然两通道的透过率的相同,但由于进入通道B的信号是通道A上的反射信号,所以风速为零时,透过两通道的能量也不相等,但较传统离散双F-P标准具的效率更高[39-40]。
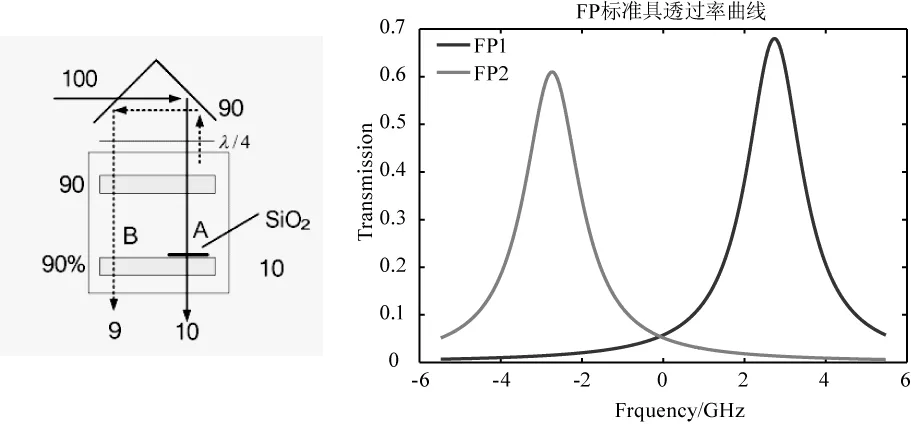
图3 连续双边缘F-P标准具示意图及双边缘透过率Fig.3 Schematic of continuous double-edge F-P interferometer and double-edge transmittance
Chanin依托于双边缘的高敏感性提出了多普勒频率响应函数R[34,41],响应函数R是多普勒频移的单值函数,从而可以利用响应函数求得多普勒频移,在风速为-100~100 m/s范围内,响应函数为一条直线,表达式为:
(9)
其中,NA和NB分别表示回波信号通过标准具两个通道的光子数,可表示为:
(10)
通过F-P标准具后光子探测器接收到的光子数由F-P标准具的透过率决定的,所以响应函数可以表示为:
(11)
其中,TA和TB分别表示F-P标准具两个通道的透过率。
响应函数廓线反映了各高度回波信号频率的变化,利用系统标定函数与大气温度廓线,可以计算出不同高度的多普勒频移[42]。Korb自1992年以来一直致力于边缘技术研究,并和Flesia提出了另一种响应函数的表达式[43-46]:
(12)
根据相同的原理,响应函数还可以表示为:
R3=T1-T2
(13)
(14)
除了Korb提出的多普勒频率响应函数之外,其他响应函数在正常风速所产生的多普勒频率范围内,敏感性都较高,但响应函数R1和R4在风速较大时略高,但是并不明显,所以在应用中需要根据实际需求选择不同的响应函数。不同响应函数曲线如图4所示。
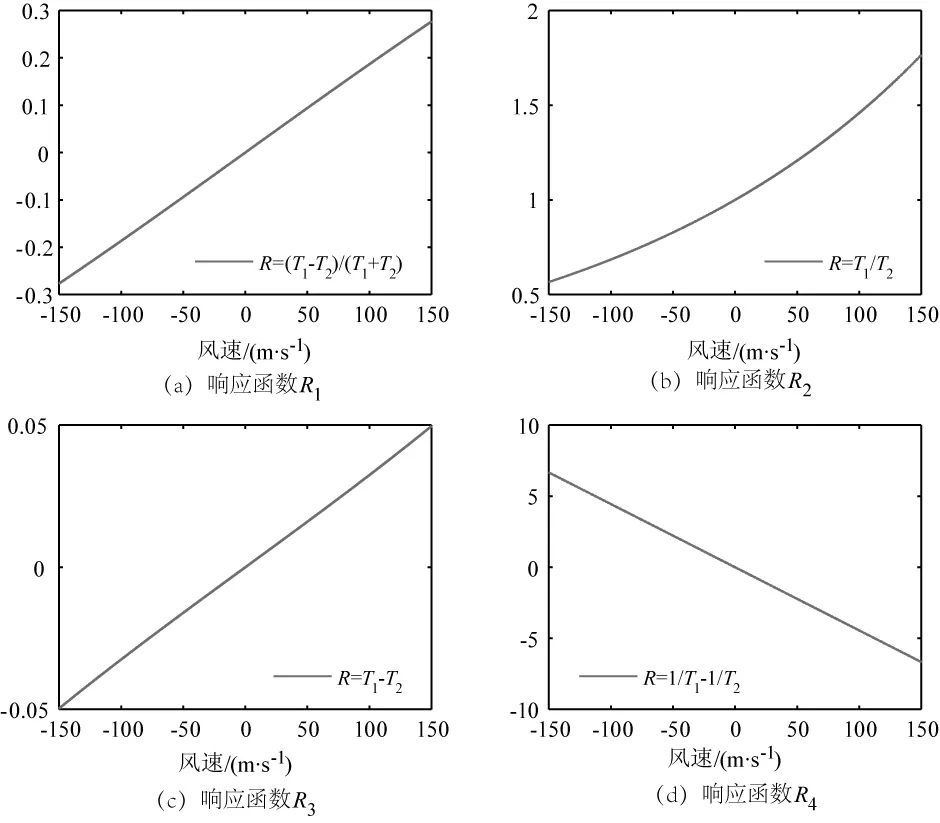
图4 不同响应函数曲线Fig.4 Different response function curves
根据响应函数的反函数便可以确定多普勒频移的大小,表达式为:
(15)
其中,R(vd)和R(0)分别为回波信号和出射激光在标准具两个通道信号的比值。
3.2 条纹技术
条纹技术是基于光透过干涉仪后干涉条纹的位置受波长影响而提出的,通过测量干涉条纹的位置变化可以获得多普勒频移[32,47],使用多通道探测器进行测量,条纹分布在各个通道上的能量随多普勒频移变化,即条纹重心发生移动,通过测量条纹重心的相对移动就可以计算风速[48]。常用的干涉仪有F-P标准具、M-Z干涉仪[29]、Michelson干涉仪和Fizeau干涉仪,但由于Fizeau干涉仪和M-Z干涉仪的干涉条纹呈线形,确定条纹重心更加简单。
Fizeau干涉仪由两块光学平板组成,两块平板之间以一定的楔角分开,回波信号通过平板间的楔形空间后,沿楔角方向形成干涉条纹,其强度分布可以用Airy函数来描述:
(16)
式中,τ和R分别为干涉仪的透过率和反射率;φ为相位因子;φ=4πdv/c;d为平板间距,可以表示为d=d0-αy,其中d0为平板中心间距;α为楔角,如果频率为v0的激光透过干涉仪后的条纹位于干涉仪的中心d0处,则频率为v0+vd的回波信号的干涉条纹位于d0v0=d(v0+vd)处,于是条纹在探测器上的位置为:
(17)
式中,vd为多普勒频率;vr为径向速度;c表示光速。由于vd≪v0,所以得到公式(17)的近似结果,最大测量速度范围由楔角α决定。Fizeau干涉仪工作原理如图5所示。
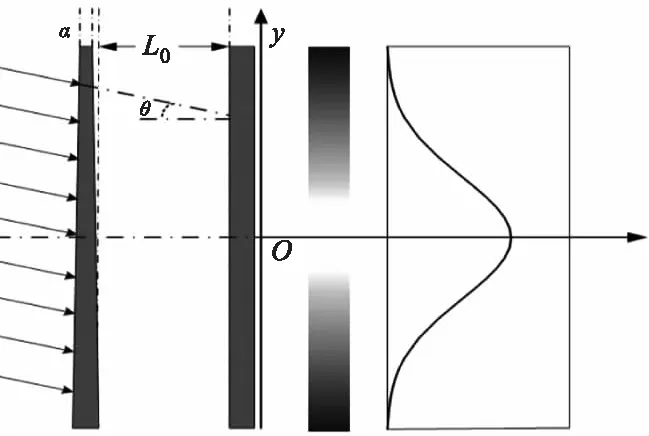
图5 Fizeau干涉仪原理Fig.5 Principle of Fizeau interferometer
回波信号通过干涉仪后被CCD探测器接收,由于条纹位置随多普勒频移发生变化,所以光透过干涉以后,CCD每一个像素单元上接收的光子数会变化,通过计算出条纹的重心,重心对应的频率便为多普勒频移,计算条纹重心的方法有重心法、高斯相关法、极大似然函数法、下降单形算法等。
3.2.1 重心法
重心法是确定条纹重心最常用的方法,由Gagne等人于1974年提出,表达式为:
(18)
其中,C为利用条纹计算得到的中心波长;k为CCD上强度最大的像元对应的序号,m=2或3;Ii为第i个条纹的强度;υi为第i个条纹的中心波长。大气的径向风速为:
vLOS=(C-8.5)×vUSR/16
(19)
式中,vUSR为有用光谱范围对应的速度。重心法的误差随风速的增大而增大,当风速超过100 m/s时,误差会有一个较大的跃变,这是由风速大小造成的,称之为边缘偏差,并且计算结果具有周期性振荡。重心法计算的重心位置和误差如图6所示。
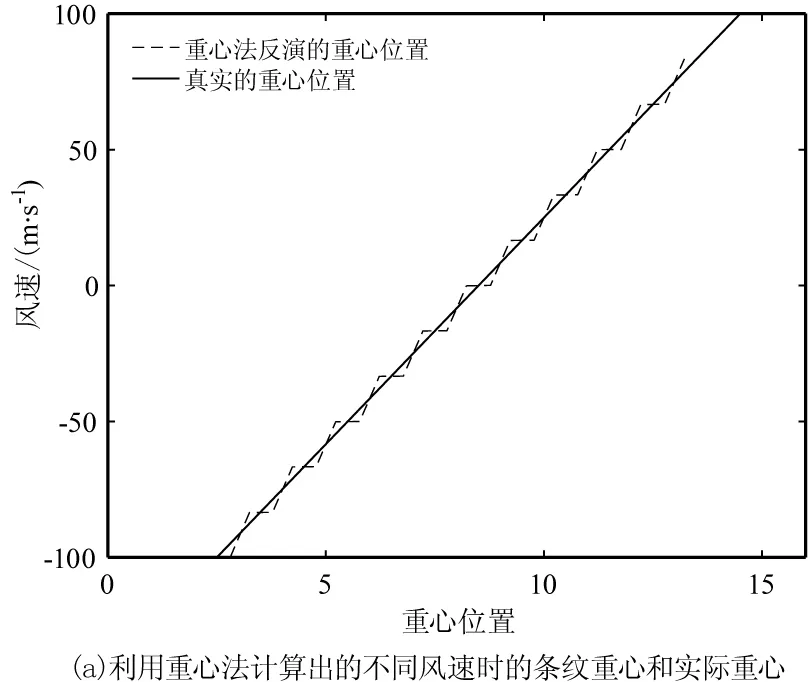
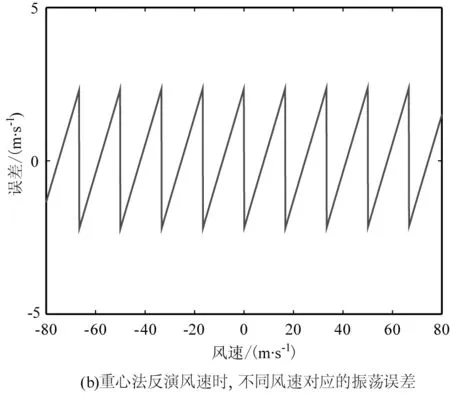
图6 重心法计算的重心和误差Fig.6 Orthocenter and error caculated by using centroid method
3.2.2 高斯函数拟合法
假设探测器上的信号服从高斯线形,当它的一级导数为零时,函数达到最大值,该值对应频率便为多普勒频移。高斯函数与波长和半峰全宽有关,其表达式为:
(20)
其中,Ii为信号强度;λi为波长,则第i个条纹间隔内高斯函数的表达式为:
(21)
式中,imax为用于计算的条纹序号的最大值;λ0为中心波长,为了确定高斯曲线的最大值,假设函数的一级导数为0,则:
(22)
通过计算导数得到λ0便可计算风速。这便要求预先设定一个λ0的值进行迭代,通过计算λn和增加步长来计算得到λn+1,其反演算法写为:
(23)
该方法需要提前假设一个未知参数,即高斯函数的半峰全宽ΔλFWHM,其数值大小和信号在探测器上的半峰全宽FWHM非常接近,输入不同的FWHM,将会导致不同的系统误差,当风速较大时(超过50 m/s),也会出现和重心法相同的误差跃变。当输入的ΔλFWHM较大时,这种误差跃变会更明显,灵敏度会减小。不同风速时的条纹分布及高斯函数拟合曲线如图7所示。

图7 不同风速时的条纹分布及高斯函数拟合曲线Fig.7 The fringe distribution and the curve of gaussian function fitting of different wind velocity
3.2.3 极大似然函数法
对于多通道探测器而言,每个通道上的光子数是光谱宽度、多普勒频移、自由光谱区间及系统接收总能量的函数,且每一通道探测到光子数的概率服从泊松分布,通过定义似然函数,当似然函数取得最大值时对应的频率就是回波信号的频率。
假设NFiz(i)为CCD上第i个通道上探测到的光子数,Ni(λ)为对应通道上强度随波长的分布,用Λ表示Ni(λ)的概率密度函数,表示为检测到NFiz(i)的可能性,最大似然方法就是找到Λ的最大值来作为Ni(λ)的一个函数,该算法由Helstrom和Van Tree于1968年提出,被Frehlich、Yadlowsky和Smalikho应用于非相干激光雷达系统中[49-51]。
假设强度分布服从洛伦兹线型,密度分布函数服从洛伦兹线形并代表概率密度函数(似然函数),则洛伦兹函数可以表示为:
(24)
其中,ΔλFWHM为信号半宽,探测器上的光子数为:
Ne(λ)=ns*L(ΔλD)
(25)
式中,ns为CCD上所有的光子数,则光子的分布表示为:
(26)
其中,ΔλD为波长变化。通道i(i=1,2,3,…,16)上的平均光子数为:
(27)
Δλpix=ΔλUSR/16为每个通道的宽度,a=i·Δλpix-ΔλD-ΔλUSR/2,b=(i+1)·Δλpix-ΔλD-ΔλUSR/2。求解积分公式得到每一个通道的光子数:
(28)
将方程进行整理得到:
(29)
其中,ns和ΔλD为方程中的未知参数。最大似然函数Λ将用概率密度函数p来表示,p是关于强度分布Ni(λ)的函数:
Λ(ΔλD,ns)=∏ip(Ni)
(30)
在通道i上探测到NFiz(i)的概率p服从泊松分布,它是Ni(λ)的理论平均数和CCD上探测得到的光子数NFiz(λ)的函数(为了简便,将Ni(λ)写为Ni,将NFiz(λ)写为NFiz):
(31)
为简化后面的运算,对式(31)采用对数运算:
Λln(ΔλD,ns)=ln(∏ip(Ni))
(32)
当函数取最大值时,便可以得到ΔλD的值,根据式(31)和式(32)可得到:
(33)
(34)
式(34)等号右边第二项为探测器上探测得到的强度,是一个常数值,用C来表示,第三项为信号强度ns:
(35)
将式(28)代入式(35)中得到:
(36)
该方程无法得到解析解,所以需要进行迭代来得到近似解,未知参数ΔλD用Δλpix(ξ-0.5ΔλUSR)来替换,ξ为算法的步长宽度(通常为0.0024 pm)。
利用最大似然函数法计算风速时,误差随着风速的增大而增大,风速大于50 m/s时同样会产生跃变。
3.2.4 下降单纯形法
下降单纯形法由Nelder和Mead于1965年提出,单纯形法的基本思路是在N维空间中,构造一个非退化的初始单纯形,然后做一系列的几何操作,如反射、扩展、收缩等,逐步往极值点移动该单纯形。在一个几何体(单形)内确定一个多于一个变量的函数的极值,单形的尺度是多维的并且试图将极值限制在单形体内,在n维空间中具有(n+1)个角的最简单的几何体是三角形,计算的每一步,对单形每一个角进行分析并将效果最差的角用另一个来替换,区别于其他算法,该算法不需要求导数,并且是绝对收敛的,1988年下降单纯形法得到了具体的应用。
假设气溶胶的后向散射信号满足洛伦兹线型,在计算过程中变化的参数有FWHM(a1)和最大值的位置(a2),这两个参数可以描述多普勒频移。该算法在计算时,需要给定a1和a2,通过每一步迭代,原来的初始值会有一个改变量Δa,并与初始值结合,结合的方式有三种(a1,a2;a1+Δa,a2;a1,a2+Δa),从而每一组值产生三个洛伦兹函数,洛伦兹曲线由式(24)表示,该算法的表达式为:
(37)
式中,A为振幅,由CCD上的最大强度来决定,每一个像素点由10个点来表示,如果CCD有16个像素就会产生160个波长间隔,一系列的测试表明该种波长间隔是最优的,将产生的曲线与CCD上的信号的偏差的平方相加,三个结果代表了单形的每一个角(n=2),将每一个角的误差进行比较并将误差最大的角进行替换,如果误差达到一定的阈值,则达到了洛伦兹曲线的最优参数。该算法被用于决定信号最大值的位置和信号的FWHM。
下降单纯形法对于初始给定的FWHM的值非常敏感,相比于重心法和高斯拟合法算,下降单纯形法的误差不会随风速的增大而增大,即误差不会出现跃变。
重心法是计算多普勒频移最简单的算法,但其计算误差随风速的增大而增大,计算结果具有周期性振荡,因此在风速较大的情况下,适用性较差,并且算法会引入振荡误差;当风速较小时,最大似然法与高斯拟合法反演的风速误差相当,但高斯拟合法目标函数明确,计算速度快,易于实时处理,而极大似然法计算速度较慢,计算时间不稳定,不利于风速的实时反演,但当风速较大时,极大似然法的计算结果仍然保持较高的精度,不会出现误差的跃变,这是高斯拟合方法无法达到的。因此,实际风速反演时,可以同时利用高斯拟合和最大似然法,利用高斯拟合方法计算大风速,利用最大似然法反演小风速,风速大小则是根据CCD上条纹能量最大值所在的通道位置和光谱宽度来判定,当最大能量通道的位置接近边缘时认为风速较大。并且最大似然法反演风速受信噪比影响较大,而高斯拟合法受信噪比影响较小。
4 总 结
随着激光技术的发展和日益成熟,利用激光雷达测量大气参数已经成为一种发展趋势,而且激光雷达已经已经可以实现气溶胶后向散射系数、消光系数、偏振态、水汽混合比和大气密度等气象要素的探测,多普勒测风激光雷达可以提供高精度、高时空分辨率的探测数据,并且星载多普勒测风激光雷达可以提供全球风场信息。欧洲已经于上世纪末提出了基于激光技术的大气风场测量计划(ADM-Aeolus),这一计划的核心是研制星载多普勒测风激光雷达ALADIN(Atmospheric Laser Doppler Instrument),以获取对流层以及平流层底层的风廓线。而测风时准确的计算多普勒频移是高精度探测风场的必要条件。文章总结了非相干多普勒测风激光雷达的鉴频方式,及不同鉴频方式下多普勒频移的算法及其优缺点,并分析了不同算法的适用范围,从而可以根据不同条件选取不同的鉴频方式和鉴频算法。
目前我国多家科研单位的激光雷达研制能力达到了世界先进水平,并且已经开展星载激光雷达的研究,实现全球云、气溶胶和风场垂直结构的自主观测,以提高我国地球探测能力及气象预报和气候预测水平,促进我国科研事业的发展。相信在各单位的共同努力下,我国不同技术体制的星载激光雷达一定能够快速发展。

