含光伏发电的配电网风险评估
徐孟霞 钟成元 张二龙 陈祥平 甘新华 王富根 朱代发
(1.国网安徽省电力有限公司岳西供电公司 2.国网安徽省电力有限公司安庆供电公司)
0 引言
大量分散的分布式光伏发电在配网中应用导致潜在的未知风险难以预估[1-3]。局部风险得不到有效控制的情况下,可能会导致输电网发生大面积停电事故。针对含有大规模光伏分散接入的复杂配电网,亟待建立一套科学有效的风险评估方法及体系以准确地评估电网实时运行状态。
1 光伏发电概率模型
描述光伏发电出力特性主要有参数估计法和非参数估计法两类。前者受多种因素的影响,往往存在较大误差。而后者对总体的假定较少,避免了总体分布预判偏差或分布变化造成的错误。因此,选用核密度估计法对光伏发电随机模型进行描述。
设光伏发电输出功率P1的概率密度函数为fpv(P1),则 fpv(P1)的核估计为:

式中:K为核函数,h为光滑参数,n为样本容量。
由核密度估计理论可知,当n→∞,h→0且nh→∞时,式 (1)将收敛于可见,核密度估计的精度取决于带宽和核函数。带宽一定时,不同核函数对fpv(P1)的影响是等价的。h取值过大,会导致fpv(P1)过于平滑,出现较大的估计偏差;h取值过小,导致fpv(P1)欠平滑,密度曲线有较大的波动。
由式 (1)得到基于两个不同核函数K1(.)和的两个核估计则最优带宽选取可转化为下式的优化问题:

式中,EISE表示两个核估计函数的积分均方误差。
2 计及相关性的概率潮流计算
2.1 概率潮流基本理论
概率潮流算法根据给定的节点注入功率、电压等具有概率统计特性的原始数据,求解各节点电压和支路功率的期望值、方差和概率密度函数等概率统计特性[4]。
设X为连续型随机变量,则X不大于实数x的概率是关于x的一个函数,称此函数为随机变量X的累积分布函数,表示为:

式中,f(x)是概率密度函数。
离散型随机变量的概率密度函数为:

其累积概率分布函数为:
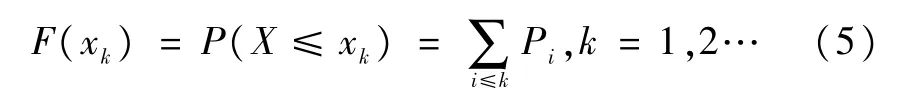
实际应用中,常采用数字特征的参数表述随机变量的基本性质。
①中心距和原点矩。设连续随机变量x的密度函数为f(x),则其k阶原点矩αk和各阶中心矩βk为:

设离散的随机变量x取值xi的概率为pi,则其k阶原点矩αk和各阶中心矩βk为:
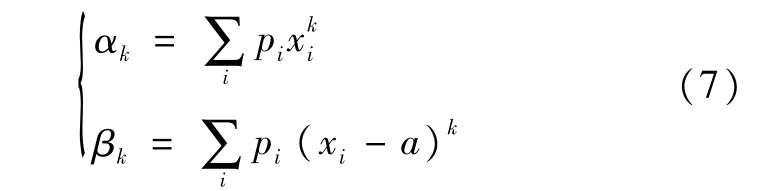

若其k阶矩存在,将特征函数φ(t)按Taylor级数展开得:

式中:γk为随机变量的k阶半不变量。
由此可知半不变量的两个重要性质:
1.相互独立的随机变量,和的各阶半不变量等于各阶半不变量之和。
2.随机变量n倍的k(k≥1)阶半不变量等于它自身的k阶半不变量的nk倍。
2.2 计及相关性的概率潮流计算
2.2.1 copula函数原理
copula函数是将多维随机变量的联合分布用其一维边际分布连接起来的函数,描述了变量间的相关性。由sklar定理可知边缘分布的联合概率分布可以实现各边缘分布之间联络关系的强提取,即copula函数是一种与所联结的边缘分布之间弱联系,具有相对独立性的,能够对边缘分布之间连接关系具有精炼表达的函数类型。copula函数构建过程主要分为两个步骤:一是各变量边缘分布的构建,二是寻找适合的copula函数并求解其参数,从而用来描述各变量相关关系。
2.2.2 线性化潮流计算模型
设W、X、Z分别为节点注入功率、节点状态变量和支路潮流变量,f为功率方程;g为支路潮流方程,则潮流方程可写成:

将上式进行泰勒级数展开,并忽略2次以上的高次项得:

式中,J0、G0为雅可比矩阵,S0、T0均为灵敏矩阵。设节点间相互独立,根据半不变量的性质可知i点注入功率的半不变量ΔWi为:

式中,ΔWGi和ΔWLi分别为节点i的发电机注入功率和负荷注入功率。
由半不变量的性质一可求得节点i注入功率的k阶半不变量为:

上式将复杂的卷积运算通过半不变量转换为加法运算,可显著降低计算量。
由半不变量性质二可求得节点状态变量和支路潮流变量的k阶半不变量为:

2.2.3 随机变量概率分布的求解
由半不变量法的计算流程可知对节点注入功率计算其各阶矩及半不变量,得出节点状态变量和支路潮流变量的各阶半不变量后利用Gram-Charlier级数反推得到状态变量的概率密度函数和累积分布函数[5]。
求得各边缘分布后,利用copula函数将其合并成一个计及相关性的综合注入变量,求取综合变量各阶矩及半不变量,再按照上述计算流程进行计算,即为copula函数所建立的综合概率模型应用于解决考虑相关性时的概率潮流计算问题。
3 大规模分散光伏接入的风险指标体系
不考虑系统故障时,建立节点电压越限和支路潮流越限以评估系统的安全风险水平。运用随机潮流计算所得的节点电压和支路潮流的概率分布及累积分布函数,可求得各节点电压和支路潮流越限的概率,再通过严重度指标即可求出配电网的风险大小[6]。
①节点电压越限风险指标
节点电压越限的概率如下:

采用电压偏移量作为风险定义中严重性后果函数,节点电压越限严重度指标如下:
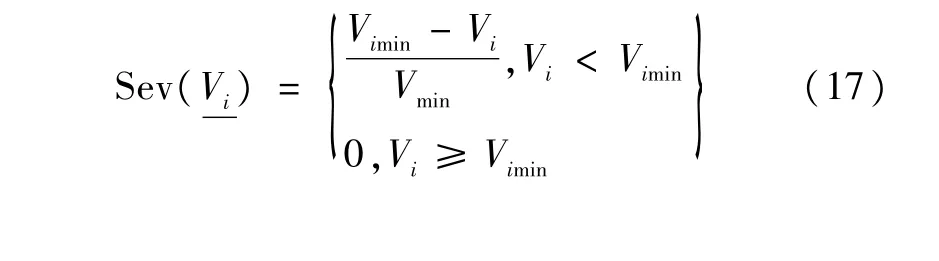


②支路潮流越限风险指标
支路潮流越上限的概率计算公式如下:

支路过载的严重度函数如下式所示:
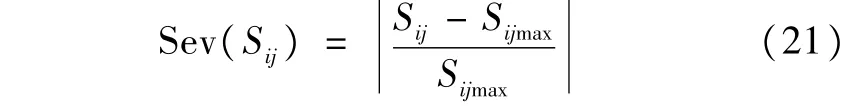
Sij为支路ij的有功潮流,Sijmax为支路ij所允许的有功潮流的上限,设其上限为未接入分布式电源情况下支路的功率期望值的1.3倍。F(Sij)表示支路潮流的累积分布函数。
支路潮流越限风险指标为:
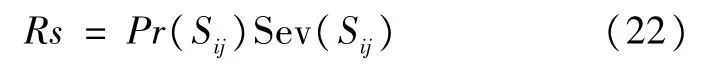
③综合指标
设有m个节点,有n个风险评估指标,形成原始数量矩阵,即

式中:i=m,j=n=2。rij为第 i个节点的第 j个指标评估值。
针对实验班和控制班的前后测成绩进行配对样本t检验,数据表明:1)两次测试的听力成绩都有显著性差异(p=0.015<0.05 & p=0.029<0.05),实验组两次测试的均值差MD=5.690,控制组两次测试的均值差MD=4.410;2)前后两次测验的口语成绩只有实验组的有显著差异(p=0.008<0.05),实验组前后测的口语成绩均值差MD=8.829,控制组前后测的口语成绩均值差MD=2.526(如表2、表3所示)。
指标权重计算步骤如下:
(1)计算i节点中第j个指标值的比重pij

(2)计算所有节点第j个指标的熵值ej
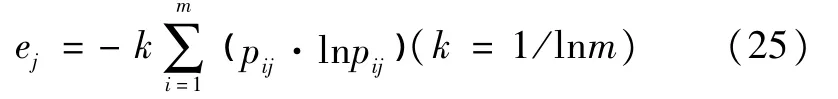
(3)计算第j个指标的熵权Wj

综合风险评估指标为:
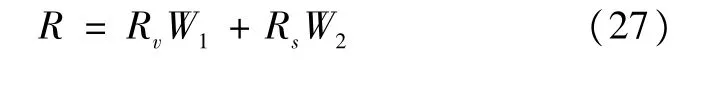
4 仿真分析
本文在如图1所示的IEEE34节点系统基础上加入分布式光伏,开展配电网风险评估的仿真分析。基准电压Vb=10.5kV,系统基准容量Sb=1MVA。
4.1 光伏数量对系统风险的影响

图1 IEEE34节点配电网示意图
建立非参数核密度估计的光伏出力模型,设节点负荷期望值为系统原始负荷值,标准差取期望值的10%。本节针对以下三种情况讨论分布式光伏接入系统的数量对配网风险水平的影响:(1)无分布式光伏接入;(2)有5个节点含有分布式光伏;(3)有10个节点含有分布式光伏。
(1)无分布式光伏接入
选取节点10、21、33的电压和支路9-10、26-28、32-34的有功,如图2、3所示。
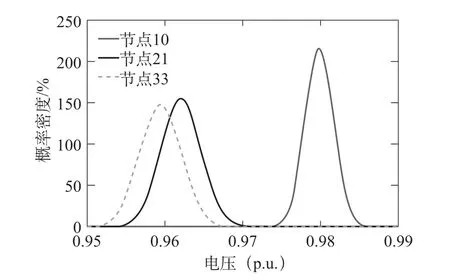
图2 节点电压概率密度分布函数曲线

图3 支路潮流概率密度分布函数曲线
(2)5个节点含有分布式光伏
光伏接入系统的2、15、20、31、34节点,结果如图4、5所示。
求出各个节点的电压越限的风险值大小如图6所示。(3)10个节点含有分布式光伏
光伏接入系统的 2、4、15、20、22、23、31、32、33、34节点,结果如图7、8所示。

图4 节点电压概率密度分布函数曲线
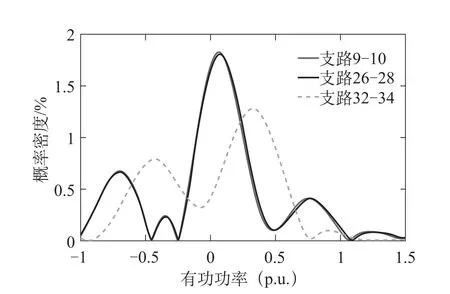
图5 支路潮流概率密度分布函数曲线
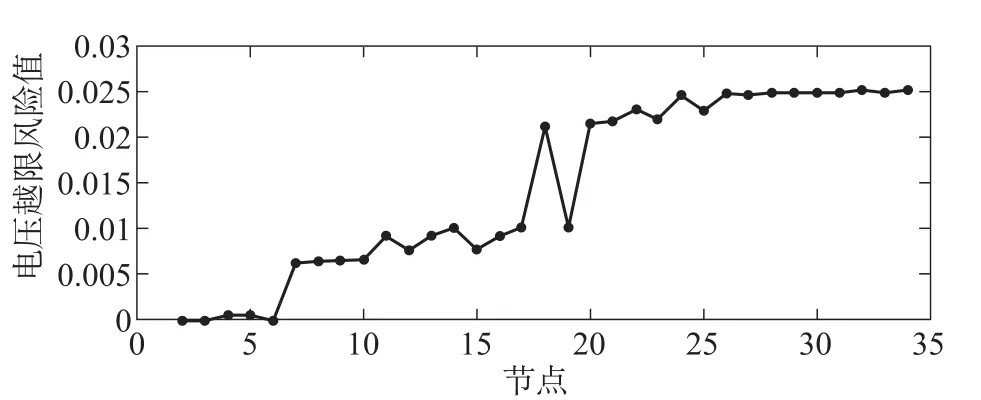
图6 各节点电压越限风险指标

图7 节点电压概率密度分布函数曲线
求出各节点电压及支路潮流越限的风险值大小如图9、10所示。
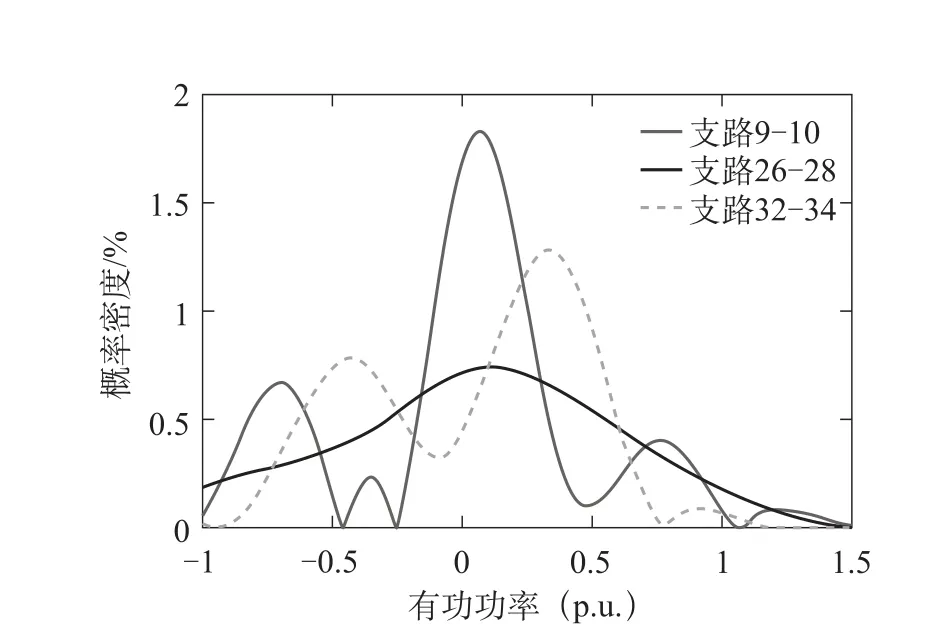
图8 支路潮流概率密度分布函数曲线

图9 各节点电压越限风险指标
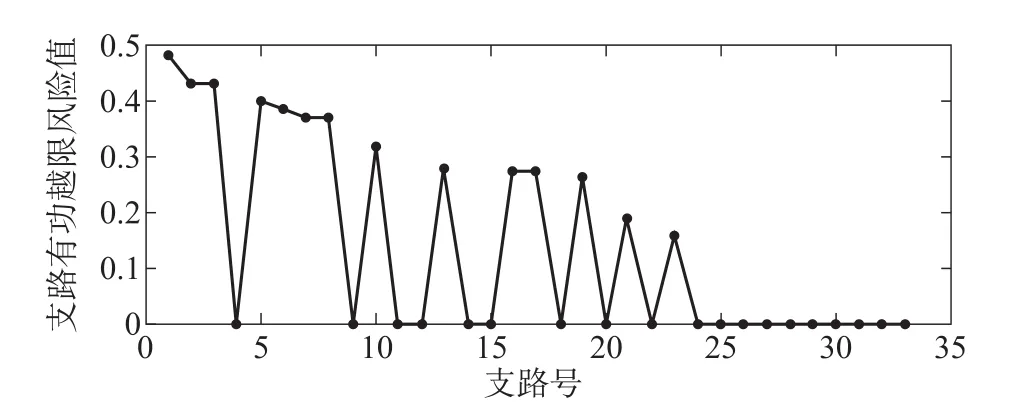
图10 各支路有功功率越限风险指标
4.2 光伏位置对系统风险的影响
将节点22的光伏接调至节点11,求该情况下风险指标大小。通过具体的数据对比分析接入位置对系统风险的影响。
(1)电压越限风险指标
光伏接入系统2、4、15、20、22、23、31、32、33、34节点时的各节点电压越限风险指标如图11所示。

图11 光伏接入后越限风险指标 (方式一)
将接入节点22的光伏调整到节点11时,各节点电压越限风险指标如图12所示。

图12 光伏接入后越限风险指标 (方式二)
从光伏接入系统不同位置的对比可知,光伏接入配电网后对电网电压的影响主要取决于节点距离光伏的电气距离。距离越近,其节点电压越限风险值会比较大。
(2)潮流越限风险指标
接入2、4、15、20、22、23、31、32、33、34节点时节点电压越限指标如图13示。
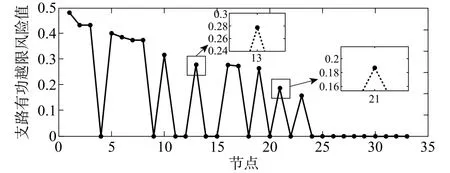
图13 光伏接入后越限风险指标 (方式一)
将接入节点22的光伏调至节点11时,各支路有功越限风险指标如图14所示。
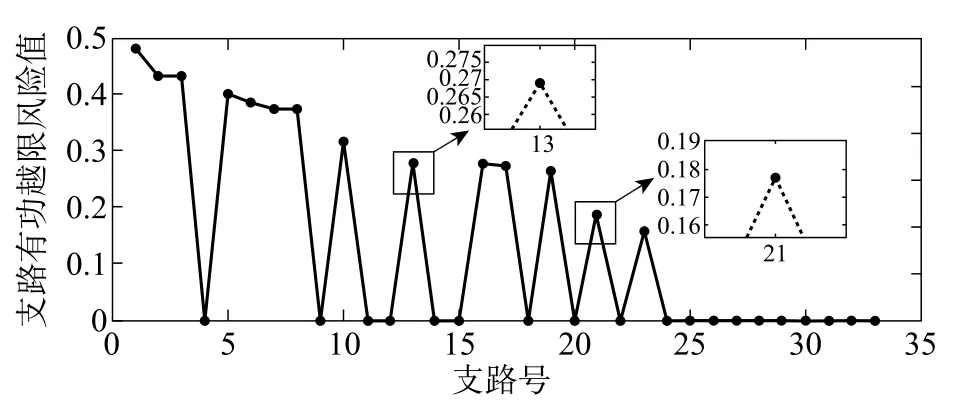
图14 光伏接入后越限风险指标 (方式二)
对比以上两种情况可知,接入位置发生变化前后,支路11-14有功越限风险值从0.28降至0.27,支路20-22有功越限风险值从0.19降至0.18以下。表明光伏接入的位置对支路潮流的风险指标具有一定的影响。
光伏接入系统的位置不同,对系统的节点电压和支路潮流越限风险影响是不同的。在实际中,应通过大量仿真模拟大规模分散光伏在不同位置接入时的风险大小,从而选择风险最小的方案接入大规模分散光伏。
4.3 综合风险指标
本文选用光伏接入系统的2、4、15、20、22、23、31、32、33、34节点时的各节点电压和潮流越限指标,采用熵权法计算综合风险指标。以节点10、13、21为例,得到综合风险指标值如表1所示。

表1 综合风险指标
5 结束语
本文利用计及相关性的概率潮流算法,对含大规模分散光伏的配电网系统进行了风险评估。
(1)建立了系统元件的随机模型,包括基于非参数核密度估计的光伏出力概率模型以及采用正态分布的负荷概率模型。
(2)建立了含大规模分散光伏的配电网风险指标。从节点电压越限和支路潮流越限两个方面分别计算越限概率和严重度指标,得出节点电压越限风险指标和支路潮流越限风险指标,再计算各指标权重得到综合指标,利用综合指标评估大规模分散光伏出力随机性给配电网运行带来的风险。
(3)开展了基于计及相关性的概率潮流算法对含大规模分散光伏的配电网进行风险评估。通过风险值的计算将系统运行中存在的风险进行量化,为大规模分散光伏的运行、规划提供了理论。

