钙钛矿超晶格的演生磁电物性

翁亚奎 ，董帅

1.南京邮电大学理学院，南京，210023 2.东南大学物理学院，南京，211189

目 录

I.研究背景181

II.晶格结构 182

III.磁性 183

A.电荷转移 184

B.应力调控 184

C.交换耦合 185

D.量子限制效应 186

IV.铁电性 187

A.杂化非本征铁电性 187

B.电子铁电性 190

V.磁电耦合 192

VI.总结和展望 195

致 谢 195

参考文献 195

I.研究背景

在新材料的设计和探索中，钙钛矿过渡金属氧化物因其丰富的物理特性备受研究者的青睐[1−4]。早在二十世纪八九十年代，钙钛矿氧化物及其衍生体系就已备受瞩目：1987年，朱经武、吴茂昆研究组以及赵忠贤团队发现YBaCuO化合物在90 K以上仍可实现超导性质[5,6]，突破了麦克米兰极限40 K的封锁，掀起了高温超导研究热潮；1994年，贝尔实验室的Jin等人在LaCaMnO薄膜中观察到低温下巨大的负磁阻效应[7]，掀起了庞磁阻研究热潮。此后，随着材料制备工艺的日臻成熟，越来越多的钙钛矿氧化物材料开始进入人们的视野，各种神奇的物性也如雨后春笋般出现。

时至今日，钙钛矿材料已经是物理性质最为丰富的一类功能材料，例如铁电材料、铁磁材料、多铁材料、高温超导材料、庞磁电阻材料、拓扑绝缘体甚至钙钛矿太阳能电池材料等[1,4,8−13]。这些丰富的材料和物理内涵已经在信息存储、医疗设施、通讯技术以及军事领域等方面大显身手。

随着多功能材料的发展，器件需要容纳和感知多种物理功能(如电、磁、光等)，而这种容纳和感知需要物性之间的相互耦合来实现。然而，在天然化合物中很难找到这类集多种功能于一体的材料。即使有，也很难应用到实际中去。

有需求便会有发展。二十一世纪初，钙钛矿氧化物又迎来了一个里程碑：Hwang等人成功制备出了原子尺度可控的氧化物薄膜异质结，并且在这两个母体绝缘的钙钛矿氧化物界面处发现了高迁移率二维电子气[14,15]，掀起了氧化物薄膜异质结的研究热潮。

相比于半导体异质结，钙钛矿氧化物异质结的物理性质则更为复杂有趣。这是由于过渡金属氧化物具有强关联特性，在异质结界面处会发生晶格重组和电子重组，从而可以改变材料的物理性质（磁性、铁电性等），甚至创造出母体材料所不具备的物性[16−19]。这些特性将为多功能器件的开发提供更多的可能性。同时，氧化物薄膜制备技术的飞速发展使得研究者可以制备出原子尺度光滑的界面、可以生长出不同晶格取向的薄膜、可以精确控制薄膜层数等，这些技术将为多功能器件的研究提供强有力的保障。

本综述将主要从钙钛矿异质结晶格结构、磁性、铁电性以及磁电耦合等方面进行讨论。

II.晶格结构

钙钛矿过渡金属氧化物丰富的物理特性与其晶格结构以及原子组成密切相关。一般来说，钙钛矿氧化物化学分子通式为 ABO3，其中 A位离子通常为三价离子（稀土离子或 Bi）或二价离子（碱土离子或 Pb），B位离子主要为3d、4d或 5d过渡金属元素，其晶格结构如图1所示。B位离子与周围最近邻的六个O形成氧八面体结构，且相邻的氧八面体共顶点连接，A位离子填充在这些氧八面体的空隙中。理想的钙钛矿是立方结构，但对于绝大多数的钙钛矿氧化物而言，它们并不是理想的立方结构，通常会发生晶格畸变。畸变类型主要有两种：(1)氧八面体的旋转和扭动；(2)Jahn-Teller畸变。

图1.钙钛矿氧化物结构示意图。(a)B位离子位于氧八面体中心；(b)氧八面体存在畸变

对于氧八面体的旋转和扭动，其主要原因是A位离子半径太小使得氧八面体发生旋转和扭动来获得更紧密的填充。为描述相对离子大小对钙钛矿结构的影响，Goldschmidt定义了容忍因子t[20]，即：

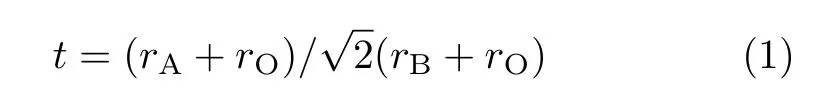
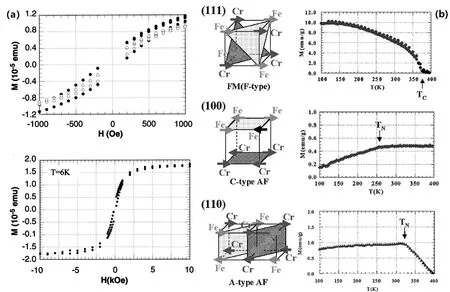
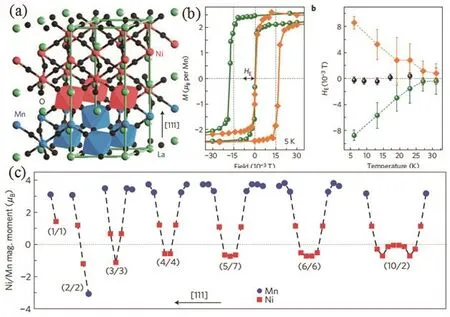
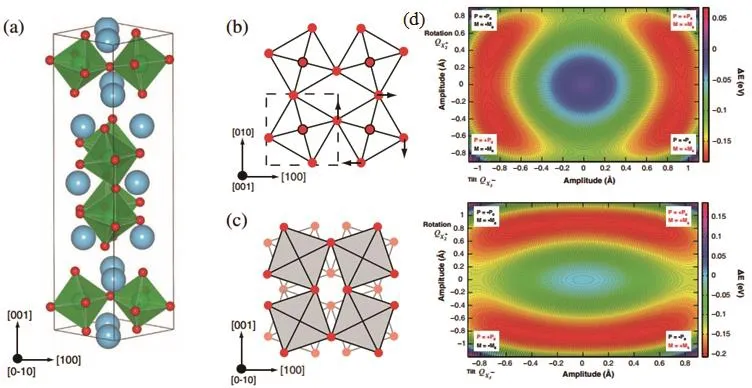
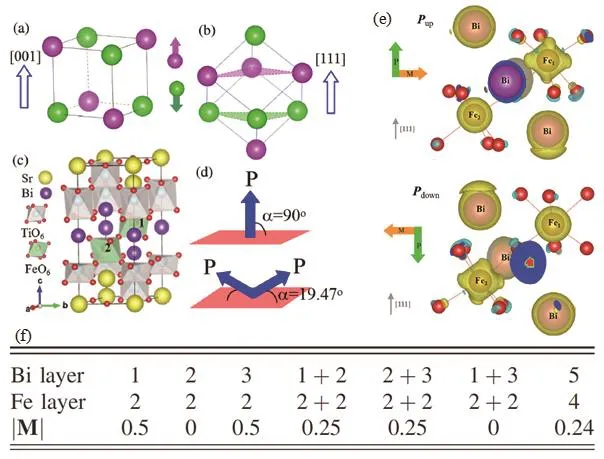
式中rA，rB和rO分别为A、B位离子和O离子的半径。当t=1时，晶格为理想的立方结构；当0.9

图2.Pbnm 正交结构：(a)扭动模式为a−a−c+，不同的颜色表示沿不同的轴扭动；(b)沿c轴方向视角，“+”表示同向扭转，δb和δa分别表示氧八面体扭动引起的A位离子反铁电位移；(c)侧方位视角，“−”表示反向扭转；(d)Jahn-Teller畸变的两种模式：Q2和Q3，箭头表示偏移量 δ，黑色箭头表示B-O键长被拉伸，蓝色箭头表示B-O键长被压缩

对于 Jahn-Teller畸变，其主要是由电声子耦合引起，其作用效果是进一步劈裂 3d能级，使eg能级去简并[27,28]。对于氧八面体而言，如果只考虑平行于B-O-B键的O离子移动，Jahn-Teller畸变包含两种简谐声子模式：Q2和Q3，如图2(d)所示。Q2和Q3在数学上定义为[29,30]：

式中δ表示沿着某个方向的偏移量。

正是由于钙钛矿氧化物蕴含了丰富的原子组分和灵活的晶格构型，其物理内涵才会令人如此着迷。然而随着科学技术的发展，自旋电子学、量子信息计算以及低能耗器件等领域对新型多功能材料的需求日益增加，研究者需要继续寻找和设计出新的多功能材料。对于新型功能材料的探索而言，其主要有两种途径，一是根据总结出来的物理规律去预测和筛选新材料。例如 2009年，Dong等人通过双交换模型计算，在 1/4掺杂锰氧化物相图中预言了一种新型的多铁相，即正交条纹相[31]。随后实验证实了符合该要求的 CaMn7O12材料确实具有磁致多铁性，多铁性温度为 90 K，并且测得其单晶铁电极化强度高达 0.285µC/cm2，是当时在块材体系中所观察到的最大磁致多铁极化[32−34]。 基于此，Long等人在该家族中又发现了两种新型多铁材料 LaMn3Cr4O12和 BiMn3Cr4O12[35,36]，这些材料为开发多功能自旋电子学器件提供了先进的材料基础。二是改造和组装“旧”材料，利用界面工程将现有的一些功能材料耦合在一起制备成超晶格，利用界面处的电子重组和晶格重组使得体系呈现出比块材更加丰富的物理和更多可调控的性能，例如电荷转移[37]，拓扑相[38]，杂化铁电[39]以及磁电耦合[4,40−42]等，如图3(a)所示。

实际上，超晶格界面处这些新奇的物理现象涉及到朗道(Landau)相变理论中两个非常重要的概念，即对称性破缺和序参量[43]。根据朗道的对称性理论，凝聚态物质中的各种有序态的出现一般都伴随着某种对称性的破缺，同时伴随着局域序参量及其长程关联的出现。如图3(b)所示，自发磁化的出现需要时间反演对称性的破缺，自发电极化的出现需要空间反演对称性的破缺，超导现象的出现需要规范对称性的破缺[44]。在钙钛矿超晶格中，界面可以破坏空间反演对称性，也可以调节体系内电子各种自由度之间的竞争，因此会诱导出许多块材所不具备的新奇物理现象。

III.磁性

对于钙钛矿过渡金属氧化物来说，磁性是最基本的一个物性。最常见的磁性包括铁磁(FM)、A型反铁磁 (A-AFM)、C型反铁磁 (C-AFM)、G型反铁磁 (G-AFM)、E型反铁磁 (E-AFM)以及 CE型反铁磁(CE-AFM)，如图4所示。其中CE型反铁磁在掺杂的锰氧化物中比较常见[45,46]。一般来说，磁结构和体系的性质有一定的关联，比如铁磁相通常情况下会呈现出金属行为，而反铁磁相通常对应电荷有序绝缘相。

图3.(a)钙钛矿氧化物超晶格中的丰富物性，取自[42]；(b)氧化物界面处关联电子对称性破缺及其物理效应

图4.常见的几种磁结构。E型和CE型反铁磁形成zigzag铁磁链，链和链之间是反铁磁耦合。取自[28]

在钙钛矿超晶格中，界面的存在使得磁性拥有了 “七十二变”：可以从有变成无，也可以从无变成有，还可以从一种磁性变成另一种磁性。这些磁性变化的内在物理机制也不尽相同，下面主要讨论以下几种物理机制。

A.电荷转移

类似于传统的半导体p−n结，在钙钛矿超晶格中，由于界面两侧的化学势不一样，电子也会从一侧转移到另一侧，以此来调节两侧的电子浓度。

例如，研究者在顺磁金属 CaRuO3和反铁磁绝缘体 CaMnO3组成的超晶格界面处发现了二维铁磁性界面[47−50]。其原因是由于电子从 CaRuO3转移到了 CaMnO3上，使得界面处的 Mn离子之间发生了双交换作用，从而呈现出了二维铁磁性界面。有趣的是，界面处 Mn的磁矩大小与 CaMnO3的层数紧密相关[50]。 对于生长在 SrTiO3衬底上的[001]取向[(CaRuO3)3/(CaMnO3)N]10超晶格，当层数N>3时，若N为偶数，界面处 Mn的磁矩为1.0µB/Mn，若N为奇数，则界面处Mn的磁矩减小为0.5µB/Mn。同时观测到的交换偏置效应也证明了界面处铁磁特性的存在，如图5所示。

图5.(a-b)CaRuO3/CaMnO3超晶格中HEB、Hc以及Ms随CaMnO3层厚度的变化；(b)10 K温度下不同CaMnO3层对应的交换偏置效应。取自[50]

类似地，在 Bhattacharya及其合作者所研究的 LaMnO3/SrMnO3超晶格工作中，尽管块材 LaMnO3和 SrMnO3分别是 A型反铁磁绝缘体和G型反铁磁绝缘体[45,51,52]，但是当两者发生原子尺度接触时，LaMnO3层的电子将流向SrMnO3层，使得(LaMnO3)2/(SrMnO3)1超晶格呈现出铁磁金属性[53−57]。

2014年，Kleibeuker等人在超晶格 LaFeO3/LaTiO3界面处发现了非常规电荷转移，该电荷转移使得整个体系的磁性消失不见[58]。对于其母体材料，块材 LaFeO3和 LaTiO3的磁基态都是 G型反铁磁[59−62]，其中 Fe3+的价电子排布为3d5(t32ge2g)，Ti3+的价电子排布为3d1(t12ge0g)。按照能带对齐(band alignment)理论，由于Ti3+离子上的电子占据态能级比Fe3+离子低，电荷是不会从Ti3+离子转移到 Fe3+离子上的，但是电荷转移确实发生了，形成了 Ti4+/Fe2+的价态。Fe离子从高自旋态变成了低自旋态，即价电子排布从3d5(t32ge2g)变成了3d6(t62ge0g)，Ti离子的价电子排布也从3d1(t12ge0g)变为了3d0(t02ge0g)，因而整个体系不呈现磁性，如图6(a)所示。随后，Zhang等人在反铁磁材料 YFeO3[63,64]以及铁磁材料 YTiO3[65,66]组成的 YFeO3/YTiO3超晶格中也发现了非常规电荷转移[67]，研究认为该类非常规电荷转移是因为材料中的能带并不是 “刚性”的能带，而是“软”的哈伯德能带。然而由于LaFeO3与 YFeO3的晶格畸变不一样[68]，因此尽管超晶格中YTiO3层的磁性消失了（Ti离子从+3价变为+4价），但YFeO3层仍保持G型反铁磁特性，并没有从高自旋态变为低自旋态，如图6(b)所示。

除了上述RFeO3/RTiO3超晶格，这种非常规电荷转移以及由其诱导的磁相转变也相继在其他超晶格中被发现，例如RNiO3/GdTiO3超晶格[69]和LaVO3/LaTiO3超晶格[70]。其非常规电荷转移内在的物理机制也相继被提出，如共价键作用、晶格畸变以及维度效应等。

B.应力调控

在材料物性的调控手段上，应力调控无疑是最直接也是最有效的。因为应力直接作用于晶格，可对晶格畸变进行直接调控，甚至改变晶格对称性，从而影响体系的电子结构和磁性。例如在RTiO3材料中，其磁性与R离子半径紧密相关，研究者便可通过拉应力或压应力来调控其磁性，进而丰富RTiO3家族的磁相图[66,71−78]。

相比于钛氧化物，锰氧化物中每个 Mn离子具有3-4个3d电子，因此研究者对其磁相的调节也更加感兴趣。Bhattacharya等人在实验中发现长在SrTiO3衬底上的 (LaMnO3)n/(SrMnO3)2n超晶格，其反铁磁奈耳 (N´eel)温度比相同组分的 La1/3Sr2/3MnO3块材 (A型反铁磁绝缘体[79−81])得到提高，A型反铁磁序得到增强[82,83]，如图7(a)所示。随后Dong等人利用双交换模型和第一性原理计算研究了 (LaMnO3)n/(SrMnO3)2n超晶格中的磁性[84,85]。计算结果表明衬底应力在增强磁性以及提高磁有序温度方面起到了关键作用。同时该磁性调制还伴随着轨道有序的调制，如图7(b)所示。此外，Dong等人还预言了在LaAlO3衬底作用下，(LaMnO3)n/(SrMnO3)2n超晶格将呈现出C型反铁磁序，为实验提供了理论指导[84]。

基于该应力调制的思路，Zhai等人制备了LaMnO3/SrTiO3超晶格，并对其晶格结构和磁性进行了研究，直接证实了面内应力对氧八面体扭动模式的调控和控制，且所调控的氧八面体扭动与磁性紧密联系[86]。

图6.(a)LaTiO3块材、LaFeO3块材以及 LaTiO3/LaFeO3超晶格的态密度，取自 [58]。(b)GGA+U以及 HSE计算的YFeO3/YTiO3超晶格态密度，取自[67]

图7.(a)左：(LaMnO3)1/(SrMnO3)2超晶格结构以及A型反铁磁序；右：La1/3Sr2/3MnO3块材以及超晶格的反铁磁序转变温度。取自 [83]。(b)左：(LaMnO3)n/(SrMnO3)2n超晶格相图结构；右：电子浓度和轨道示意图。取自[84]

与传统的双轴应力调节不同，2015年Guo等人通过稀有气体原子注入的方法，即不改变面内晶格常数，只对面外晶格常数进行调节，实现了对锰氧化物磁性和输运的调控[87]。

C.交换耦合

块材LaFeO3和LaCrO3的磁基态都是G型反铁磁，奈耳温度 (TN)分别为 750 K和 280 K[64,88,89]。1998年，Ueda等人在实验上观测到沿[111]方向生长的(LaFeO3)1/(LaCrO3)1超晶格呈现出铁磁特性[90]，如图8(a)所示，其铁磁居里温度约为375 K。随后又在 [100]和 [110]方向的 (LaFeO3)1/(LaCrO3)1超晶格中分别观测到了不同的磁序：[100]方向超晶格呈现出C型反铁磁序，[110]方向超晶格呈现出A型反铁磁序[91]，如图8(b)所示。不同晶格取向呈现出不同磁序的主要原因是由于Fe-O-Fe，Cr-O-Cr以及Fe-O-Cr的磁交换耦合作用不一样：Fe-O-Fe和Cr-O-Cr是反铁磁交换耦合，而Fe-O-Cr是铁磁交换耦合。因此，调节超晶格界面处不同的Fe/Cr分布便可以实现不同的磁序。

上述结果都是在 1:1的超晶格中观测到的。随后，Zhu等人通过理论计算不仅重现了该实验现象，还预言了LaFeO3/LaCrO3超晶格在薄膜层数更厚情况下的复杂磁序[92]。

类似地，Ichikawa等人也在 [111]取向 1/1层状堆叠的 BiFeO3/BiCrO3超晶格中发现了室温铁磁序[93]。由于界面处的 Fe-Cr之间的磁耦合作用，Nechache等人发现了外延生长的BiFeO3/BiCrO3超晶格呈现出磁性增强现象[94]。

图8.(a)[111]方向LaFeO3/LaCrO3超晶格在6 K（黑色圆点）和350 K（白色圆点）时的磁滞回线，取自[90]；(b)不同方向超晶格(1/1)的磁结构示意图及其相应的磁化强度随温度的变化关系，取自[91]

D.量子限制效应

2012年，Gibert等人在沿 [111]方向生长的LaNiO3/LaMnO3超晶格中发现了交换偏置现象，如图9(a-c)所示，而沿着 [001]方向生长的超晶格（与 [111]方向超晶格具有相同的晶格成分）却没有交换偏置效应，这些物理现象引起了研究者的极大兴趣[95]。首先，块材 LaMnO3是 A型反铁磁莫特绝缘体[45]，其薄膜形态较容易呈现出铁磁性[55−57,86,96−100]，而块材 LaNiO3则是顺磁金属[101]。 我们知道，交换偏置现象通常出现在同时包含铁磁和反铁磁的体系中，那么该超晶格 LaNiO3层中的反铁磁序是怎么来的？为什么具有同样成分的[001]方向超晶格没有交换偏置效应？

随后，Dong等人通过理论模型计算，发现量子限制效应在超晶格中起到了至关重要的作用[102]，即量子限制效应导致了原本顺磁的LaNiO3在超晶格中出现了磁性。量子限制效应与超晶格生长方向密切相关，如图10(a)和 (b)所示。在 [111]方向生长的超晶格中，量子限制效应最强，因此LaNiO3层具有较强的磁性，这可能是实验观察到交换偏置的起因。而[001]方向的量子限制效应很不明显，因此几乎无法诱导出 LaNiO3层中的磁性，对应实验上没有观察到交换偏置现象。尽管在LaNiO3/LaMnO3超晶格中也发现了Ni3+离子与Mn3+离子之间的电荷转移现象[98,103,104]，但电荷转移的作用却不如量子限制效应，因为[001]取向的超晶格中也存在电荷转移，但并没有诱发 Ni磁性。此外，Dong等人还理论预言了 [110]方向超晶格中的磁性诱导效应介于 [001]与[111]方向之间，有待实验的进一步验证[102]。

图9.(a)[111]方向 LaNiO3/LaMnO3超晶格示意图；(b)[111]方向超晶格的交换偏置现象以及交换偏置场随温度的变化;(c)第一性原理计算得到的不同Ni/Mn层的离子磁矩大小。取自[95]

实际上，钙钛矿超晶格对磁性的调制除了上述几个方式以外，还包括界面极化调控[105]，氧空位调控[106]等。研究者利用这些调控手段不仅预言了许多新奇的物理现象（如磁拓扑相[38,107−112]），还为实际应用奠定了坚实的基础，例如铁磁/反铁磁超晶格的交换偏置效应已经在磁存储领域大显身手。

图10.(a)[001]、[110]、[111]方向超晶格示意图；(b)量子限制效应导致磁性示意图。取自[102]

IV.铁电性

钙钛矿氧化物超晶格的“无中生有”本事不仅体现在磁性上，还体现在铁电性上。本节将重点讨论杂化非本征铁电性以及电子铁电性。

A.杂化非本征铁电性

对于 BiFeO3和 PbTiO3等本征的铁电材料，它们的铁电性来源于铁电活性离子（Bi3+或 Pb2+）与阴离子之间的共价配位及杂化，使得体系空间反演对称性破缺，从而产生铁电畸变[113−116]。然而，还有另外一些铁电材料，如六角晶格RMnO3(R=Ho,Y,Lu)和RFeO3(R=Lu,Yb)，它们的离子成分无论是R3+还是Mn3+或Fe3+均不是铁电活性离子，其铁电性仅来源于晶格畸变（反铁电畸变），与电子成键没有关系，被称为“几何”铁电体，即非本征铁电。这类铁电材料的铁电极化大小在 4∼10µC/cm2左右，虽然比传统的铁电材料小一个数量级，但要远高于磁致铁电材料的数值，而且铁电转变温度基本都在室温以上[9,117−125]。

2008年，Bousquet等人发表了关于非本征铁电性的开创性工作，在短周期的钙钛矿超晶格PbTiO3/SrTiO3中发现了非本征铁电性[126]。如图11所示，在 1/1超晶格体系的基态中，铁电FEz与反铁电畸变AFDzi和AFDzo共存且相互竞争，分别对应相互独立的序参量Pz，ϕzi和ϕzo。 由于这里的铁电畸变不稳定性FEz是可被抑制的，Pz就不再作为主要序参量出现。其非本征铁电性就是由界面处氧八面体的面内旋转和面外倾斜所导致。由于铁电极化是由反铁畸变位移引起的,与氧八面体中的离子无关,因此如果氧八面体中心是磁性离子，就很有可能实现一种新的磁电耦合机制。这项工作为人们探索磁电耦合效应拓宽了新的途径，并由此引发了在超晶格中利用氧八面体倾转畸变来实现高温磁电耦合的一系列奇思妙想。

图11.空间群为P4/mmm的PbTiO3/SrTiO3超晶格所包含的三种不同畸变模式：(a)FEz;(b)AFDzo;(c)AFDzi。取自[126]

沿着这条脉络，2011年Benedek和Fennie理论研究了 Ruddlesden-Popper型氧化物材料 Ca3Mn2O7，并提出了杂化非本征铁电(hybrid improper ferroelectric)的概念[39]。如图12所示，Ruddlesden-Popper型结构是以阳离子为间隔的层状钙钛矿，包含两种反铁电畸变模式旋转模式和倾斜模式，这两种模式的结合使得体系空间群为A21am，其点群为极化点群。在朗道能量项中，这个作用效果可以表示为三阶线性耦合其中a是耦合系数，P是沿[010]轴的极化，是畸变的程度。理论预测Ca3Mn2O7的极化大小约为5µC/cm2(Ca3Ti2O7为 20µC/cm)，转变温度在 500∼600 K，远高于室温[127]。2015年 Oh等人成功生长出了 (Ca,Sr)3Ti2O7单晶,并在室温下利用 PUND(positive-up-negative-down)方法测得了电滞回线[128]。

在深入探索这一新型材料的过程中，研究者总结了利用氧八面体反铁电畸变设计杂化非本征铁电的规律，以求更有目的更有效率地去寻找新材料。2012年，Rondinelli和Fennie系统研究了层状钙钛矿异质结 (ABO3)1/(A′B′O3)1中的杂化铁电性[129]。研究发现钙钛矿超晶格仅通过两者之间特殊的氧八面体扭动便可产生铁电极化，其母体材料不需要呈现出铁电极化特性。要实现杂化非本征铁电的关键点在于体系需要满足两个准则，即化学准则和能量准则。根据化学准则，只有超晶格 (ABO3)1/(A′BO3)1可以打破反演对称性，而 (ABO3)1/(AB′O3)1却不能。这是由于A位和B位有不同的反演对称性，如图13(a-c)所示。与此同时，能量准则要求 ABO3和 A′BO3需同时包含Q1(=a0a0c+)和Q2(=a−a−c0)的扭动模式（注：这里的Q指的是氧八面体扭动模式，与前文的Jahn-Teller畸变模式Q无关），如图13(e)和(f)所示。

图12.(a)Ca3Mn2O7的铁电基态A21am结构；(b)X+2旋转模式；(c)X+3旋转模式；(d)4个结构畴和可能的电控磁路径。取自[39]

基于上述两个准则，Rondinelli和Fennie列举了几个例子，如图13(d)所示。对于 YaAlO3/YGaO3和 LaAlO3/BiAlO3异质结来说，由于完全不具备或只具备其中一个准则，所以没有极化产生；而对于LaGaO3/YGaO3和LaAlO3/YAlO3异质结来说，由于同时满足了化学准则和能量准则，所以产生了杂化铁电，但由于a−a−c+扭动模式强弱不同，所以杂化非本征铁电性也呈现出不同的大小。

上述关于在超晶格中利用氧八面体畸变实现杂化非本征铁电的设计原则是基于对称性的朗道理论，纯粹从化学和结构的角度进行了讨论。2014年，zhao等人以钙钛矿超晶格 (ABO3)1/(A′BO3)1为研究对象，利用解析推导和绘图分析方法，通过原子间相互作用关系（A位离子反铁电位移和BO6八面体扭转倾斜）推导出了杂化非本征铁电性的原子理论[130]。利用这一微观理论方法可以直接看出 A位离子反铁电位移和BO6八面体倾斜对杂化非本征铁电性的贡献，这使得我们对杂化非本征铁电性的起源有了更深刻更直观的理解。在该工作中，zhao等人首先验证了前人文献提出的A位离子位移与BO6八面体之间的原子间相互耦合能量项∆E1和∆E2，成功的在原子尺度上重现并解释了 [001]和 [111]取向的 (ABO3)1/(A′BO3)1超晶格体系所存在的杂化非本征铁电性以及为何沿着[110]晶向生长的超晶格不具有铁电极化的问题，这与之前的文献报道一致[21,131−134]。此外，zhao等人还研究了具有a−a−c+扭转类型的 (ABO3)m/(A′BO3)n超晶格中杂化非本征铁电性的层数 (m和n)效应，并以 [001]晶格取向的 (LaFeO3)m/(YFeO3)n为例展开讨论，如图14所示。当m和n均为偶数或为一奇一偶时，其空间群分别为P21/c和Pbnm，体系不具有杂化非本征铁电性。只有当m和n均为奇数时，体系才具有杂化非本征铁电性(空间群为Pmc21)，极化方向沿着赝立方[110]取向，极化强度P大体与层数 (m+n)成反比[130]。

图13.(a)理想ABO3型钙钛矿在A位和B位都有反演中心；对称操作为三重旋转对称性；(b)在A/A′层状结构中，反演中心在B位(四重反演对称性)；(c)在B/B′层状结构中，反演中心在A位(四重反演对称性)；(d)钙钛矿异质结中杂化非本征铁电性需同时满足化学准则和能量准则；(e)氧八面体Q1(a0a0c+)；(f)氧八面体Q2(a−a−c0)转动模式。取自[129]

图14.[001]取向的 (LaFeO3)m/(YFeO3)m超晶格在不同的n与m组合条件下,其非常规铁电极化强度与稀土阳离子La百分比的关系。取自[130]

从上述利用超晶格实现杂化非本征铁电性的讨论中，我们似乎可以预见只有超晶格 ABO3/A′BO3才是其 “正统继承人”，而 ABO3/AB′O3是不具备竞争力的。直到2015年Zhang等人在研究(YFeO3)n/(YTiO3)n超晶格时发现，尽管(ABO3)1/(AB′O3)1不呈现出杂化非本征铁电性，但是 (ABO3)2/(AB′O3)2却呈现出铁电极化，极化方向沿着b轴，极化大小约为1.01µC/cm2，该工作对原有杂化铁电理论框架作了补充，使其更加完整[67]。 对于 (YFeO3)2/(YTiO3)2超晶格体系，铁电极化来源如图15(a-c)所示。晶格畸变导致Y3+离子和O2−离子偏离了它们原来的高对称位置，且 B位离子沿c轴方向的排列形成了...Ti-Ti-Fe-Fe...的模式，该模式类似于第二类多铁中的 ...↑-↑-↓-↓... 自旋模式 (如 Ca3CoMnO6[135],o-HoMnO3[136,137],BaFe2Se3[138])，从而打破了体系空间反演对称性，最终导致极性结构的出现。从晶格对称性上也可以分析出该超晶格空间群为Pmc21，点群为mm2(极化点群)，和上述超晶格 (LaFeO3)1/(YFeO3)1空间群一样。此外，该工作还用点电荷模型估算了Ti-O八面体，Fe-O八面体以及Y-O二十面体对总极化的贡献，如图15(d)和(e)所示。从三者的贡献中(Ti-O八面体贡献−144%，Fe-O八面体贡献+82%，Y-O二十面体贡献+162%)可以清楚地看到Y-O二十面体对总极化的贡献是最大的。Ti-O八面体对极化的贡献为负的原因可以认为是由Y-O二十面体的铁电性所形成的内部电场导致。在该体系中，由于Ti3+和Fe3+之间存在电荷转移，电子从Ti3+转移到Fe3+上导致Ti3+变成了铁电活性离子Ti4+，从这个角度来说，该体系既存在杂化非本征铁电性又存在本征铁电性。根据Zhang的计算，改变计算参数U值可以使得(YFeO3)2/(YTiO3)2超晶格体系变为金属，从而实现极化和金属性共存，其中金属性的存在可以抑制本征铁电而对杂化非本征铁电并无影响。

2017年，Weng等人利用第一性原理计算同样在(LaTiO3)2/(LaVO3)2超晶格中预言了极化与金属性可以共存[70]，究其原因，依旧是通过Ti3+与V3+之间的电荷转移以及 (ABO3)2/(AB′O3)2中晶格畸变使得两者共存。与YFeO3)2/(YTiO3)2超晶格不同的是，(LaTiO3)2/(LaVO3)2超晶格中金属性的出现对于计算参数U不敏感，且所计算的可能磁性都是金属性，也就是说金属性比较稳固。更多关于金属铁电的文章可参考文献[139−144]。

图15.(a)n=1超晶格畸变示意图；(b)和(c)n=2超晶格畸变示意图；箭头表示Y3+离子的位移；(d)Y-O二十面体、Fe-O八面体以及Ti-O八面体示意图；(e)不同U值下，用点电荷位移估算的各部分极化对总极化的贡献。取自[67]

诚然，从实际应用而言，研究者最终想实现的目标就是需找室温或高温下实现多铁序参量的共存和耦合。基于上述杂化非本征铁电性理论，Zhao等人利用第一性原理研究了沿[001]方向生长的R2NiMnO6/La2NiMnO6双钙钛矿超晶格[145]，如图16(a)所示。稀土基双钙钛矿R2NiMnO6（R为稀土元素）是典型的铁磁半导体，其铁磁居里温度大体随稀土离子半径的减小（即化学压的增加）而线性下降[146]，其中 La2NiMnO6的铁磁居里温度可达到 287K左右[146,147]。尽管R2NiMnO6体系并不是铁电体，但却具有a−a−c+氧八面体旋转伴随出现的反铁电位移，因此可通过变化R离子半径调控超晶格的电极化和铁磁居里温度。研究发现，随着R2NiMnO6/La2NiMnO6双钙钛矿超晶格中R离子的半径变化，超晶格极化强度以及铁磁居里温度也发生相应的变化，如图16(b-d)所示，其中Ce2NiMnO6/La2NiMnO6超晶格极有希望成为室温多铁材料。

图16.(a)R2NiMnO6/La2NiMnO6超晶格P21基态结构，绿色、橙色、蓝绿色、紫色及红色表示 La3+,R3+,Ni2+,Mn4+和O2−离子；(b)极化强度随R离子半径的变化；(c)铁磁转变温度随R离子半径的变化；(d)磁化强度随R离子半径的变化。取自[145]

B.电子铁电性

在一些强关联电子体系中,电荷载流子在一定条件下会发生局域化,以一种有序的形式局域在不同的离子格点上，形成周期排列的结构,也就是电荷有序态。如果电荷有序排列方式破坏了空间反演对称性，体系就会呈现出电偶极矩和宏观铁电极化，这一铁电性被称为电子铁电性[148−149]。由于电子铁电性起源于电子关联，电子的电荷、轨道和自旋自由度之间耦合会非常强烈,因此电子铁电性可能为关联电子体系中实现铁电性、磁性和其他性质的相互调控提供另外一种途径。

对于单相电荷有序型多铁材料，最典型的两种氧化物是 Fe3O4[150]和 Pr0.5Ca0.5MnO3[151−152]。 对于Fe3O4，当温度在124 K左右时，体系会发生金属绝缘体转变（Verwey转变），在转变温度之下，Fe2+和 Fe3+离子有序排列。对于 Pr0.5Ca0.5MnO3，在一定的温度之下,Mn3+和Mn4+离子在晶格上有序排列。它们所形成的Fe2+/Fe3+或Mn3+/Mn4+电荷有序态都会导致反演对称性破缺，从而产生铁电性。然而上述这两类材料带隙很窄且电导率很高，实验上很难给出直接的证明来证实其电极化的存在。此外，还有争议较大的 LuFe2O6材料，前人研究报道其Fe2+和 Fe3+特殊的双层堆栈方式破坏了空间反演对称性，可能诱导出电偶极矩并产生宏观电极化[153]，然而随后的研究对其铁电性及其来源提出质疑，争议较大[154,155]。2017年，Lin等人发现过渡金属氟化物LiFe2F6材料是一种电荷有序型多铁材料，其铁电性是由Fe2+/Fe3+电荷有序态导致，且计算得到的铁电极化很大[156]。 在应力调控下，体系可呈现出净磁矩亚铁磁铁电态，并可实现完全的电控磁效应。该研究为电荷有序型多铁材料的探索及调控提供了借鉴。

图17. (a-d)一维链中电荷有序诱导铁电性示意图：(a)格点中心电荷有序；(b)键中心电荷有序；(c)格点中心以及键中心电荷有序；(d)A1A2BA1A2B的超晶格，其中 A1和 A2为钙钛矿过渡金属氧化物材料 A的不同价态。(e)(LaFeO3)2/(LaTiO3)1超晶格示意图。(f)LaTiO3层与LaFeO3层之间的电荷转移及其诱导的铁电性示意图。取自[157]

虽然这种电子铁电性在磁电调控上有很大的潜力，但是目前研究相对较少，主要集中在掺杂的锰氧化物及部分铁基材料中。为打开这一局面，研究者开始将目光转移到钙钛矿过渡金属氧化物超晶格上面。由于过渡金属的多价态特性，将其做成超晶格后可利用界面特性打破空间反演对称性，使其产生电荷有序态，从而获得电荷有序型铁电性。而且由于钙钛矿过渡金属氧化物多是磁性材料，所以可以实现基于电荷有序的多铁材料。2016年，He等人提出了一种在钙钛矿过渡金属氧化物超晶格中设计电荷有序型铁电性的方法[157]，如图17所示。一般而言，电荷在实空间有序分布有两种方式，即格点中心电荷有序相(sitecentered charge ordering)和键中心电荷有序相(bondcentered charge ordering)，如图17(a)和(b)所示。格点中心电荷有序相是指某一离子的两个不同价态在晶格上有序交替排列，相邻格点位置电荷不等价。键中心电荷有序相是指载流子不是局域在某一格点上，而是局域在键中心，相邻两个键不等价。这两种电荷有序相由于都没有打破空间反演对称性，所以并不能独立地产生铁电性。如果将两种电荷有序相合二为一，则可以产生铁电性，如图17(c)所示。He等人的设计方法便是在具有不同价态A1和A2的钙钛矿过渡金属氧化物材料A中插入B材料，形成A1A2BA1A2B的超晶格，如图17(d)所示。若将A2-B-A1看成一种键，它将和A1-A2键形成有序，这样键中心电荷有序相和格点中心电荷有序相都存在于超晶格中，因此会诱导出铁电性。

为验证这一理论方法的正确性，He等人设计了沿 [111]方向的 (LaFeO3)2/(LaTiO3)1超晶格[157]，如图17(e)所示。Ti3+和Fe3+之间存在电荷转移，电荷转移有两种可能的情况（如图17(f)所示）：(1)Ti3+上电子向左右两个 Fe3+转移的概率相等，形成Fe+2.5/Fe+2.5金属相；(2)Ti3+上电子只沿一个方向转移，形成Fe2+/Fe3+的电荷有序绝缘相，从而产生铁电性。计算表明形成Fe2+/Fe3+的电荷有序绝缘相能量更低，更稳定，因此实现了电荷有序型铁电性。

随后，2017年 Park等人在 [001]取向的(ABO3)n/(A′BO3)m超晶格中也发现了电荷有序型铁电性[158]。根据前文讨论我们知道，在该类钙钛矿超晶格中存在杂化非本征铁电性。那么在一定条件下(合适的材料、适当的层数)，该类超晶格同样也会呈现出电荷有序型铁电性。Park等人以1:1的LaVO3/SrVO3钙钛矿超晶格为例进行了研究。计算结果发现超晶格中V离子的价态并不是混合的+3.5价，而是形成了三种可能的电荷有序反铁磁莫特绝缘态：棋盘型电荷有序相(checkerboard-type charge order)、条纹型电荷有序相 (stripe charge order)、层状电荷有序相 (layered charge order)，如图18所示。对于棋盘型和条纹型电荷有序相，沿z轴的极化为0，而层状电荷有序相沿z轴的极化不为0。根据上节讨论我们知道，由晶格畸变导致的杂化非本征铁电性方向是沿着面内的（计算得到极化大小约为4µC/cm2），面外不会产生杂化非本征铁电性，因此这里沿z轴方向的极化纯粹是由电荷有序引起的，其极化强度在17∼34µC/cm2左右。

图18.(a)[001]取向的(LaVO3)1/(SrVO3)1超晶格中三种可能的电荷有序态：棋盘型电荷有序态、条纹型电荷有序态以及层状电荷有序态。取自[158]

实际上，2015年 Bristowe等人在超晶格(RTiO3)1/(ATiO3)1中也发现了Ti3+/Ti4+的棋盘型电荷有序相，尽管该类电荷有序相不产生铁电性，但对体系的铁磁性及绝缘特性均起到了至关重要的作用[159]。

V.磁电耦合

多铁性将两种或多种铁序纳入一体，丰富了凝聚态物理的内涵，扩大了我们的视野。自 2003年 BiFeO3薄膜[160]和 TbMnO3单晶多铁性的发现[161]，多铁材料的研究便拉开了序幕，进入了蓬勃发展时期。

多铁材料最直接的应用就是磁性与铁电性的相互调控，即磁电耦合效应，如图19所示。兼具磁性与铁电性的磁电耦合材料能够进一步提高信息存储密度、读写速度。因此，深入理解磁电耦合的物理，根据物理寻找性能优越的磁电材料，并将其设计成具有磁电耦合功能的器件原型，一直是研究者所追求的目标[4,10,162−166]。

尽管磁电耦合材料前景广阔，但挑战也是巨大的。从物理的角度来说，磁和电具有独立的对称性，磁性破坏时间反演对称性，铁电性破坏空间反演对称性，两者在量子层面上是互斥的[167]。从材料的角度来说，已知的多铁材料普遍性能不佳，要将其运用到具体的器件当中，仍需解决一些关键问题[4,9,168]。首先，需要提高多铁特性，比如铁电转变温度TC、磁矩M、极化强度P。其次，需要增强磁电耦合强度。

图19.多铁性及磁电耦合示意图

对于单相多铁材料，研究者已经揭示了多种物理机制来实现磁电耦合效应，如Dzyaloshinskii-Moriya(DM)相互作用、交换收缩机制等[136,137,169−172]。 对于钙钛矿超晶格，其材料及磁电调控手段则更加丰富。例如可通过交换偏置效应实现磁电耦合，其物理思想是将反铁磁铁电材料（如 BiFeO3）与铁磁材料组成多铁异质结，通过外加电场改变薄膜材料的自旋排列，从而调控界面的交换偏置效应。Yu等人在钙钛矿氧化物超晶格La0.7Sr0.3MnO3/BiFeO3中观测到了显著的交换偏置效应[173]，如图20(a-c)所示，La0.7Sr0.3MnO3呈现出矫顽场的增强和交换偏置场。由于轨道杂化作用，界面处呈现出轨道重构的现象，通过超交换作用，界面处的锰离子与BiFeO3中的铁离子紧密耦合在一起，使得体系在BiFeO3界面处产生了宏观磁矩，且该界面磁矩与交换偏置作用具有相同的转变温度。因此可以通过BiFeO3的铁电极化来控制界面处的轨道占据，从而调控Mn-Fe之间的磁耦合。随后，Wu等人通过磁输运测量展示了该体系中电场对磁交换偏置的调控[174]，如图20(d)所示。随着外加电压的改变，铁磁层的矫顽场和磁电阻都随之发生变化，并且在连续的正、负脉冲电压下可进行重复性的调控。由于该类材料在磁电耦合效应中所存在的物理内涵和应用潜力，其交换偏置机理成为研究热点。为深入了解其物理内涵，Dong等人提出了两种导致交换偏置的新机制[175,176]，即DM相互作用和铁电极化机制。这两种物理机制都不依赖于表面处的非补偿磁矩，而与界面处氧八面体扭动有关，其中铁电极化驱动的交换偏置只存在于具有多铁材料的异质结中。

图20.(a)LSMO/BFO中交换偏置效应；(b)XMCD以及交换偏置的温度依赖；(c)界面轨道重重构及超交换作用；取自[173]。(d)电控交换偏置效应；取自[174]

此外，通过铁电场效应（如图21(a)和 (b)所示） 来实现磁电耦合也是多铁异质结的关注重点。Vaz和 Leufke等人在研究 Pb(Zr0.2Ti0.8)O3/La1−xSrxMnO3(PZT/LSMO) 时发现[177−179]，磁电耦合系数不仅随着温度变化，而且随着PZT极化方向的翻转发生巨大变化，如图21(c)所示。原因在于PZT的极化方向翻转时，会在其异质结界面处出现正负电荷的积累，从而使LSMO的空穴载流子浓度增大（减小），导致铁磁性增强（减弱），居里温度升高（降低）。这种通过铁电场效应来调节界面处的载流子浓度，进而实现磁电耦合的方法引起了研究者的广泛关注。为了揭示其中更加普适的物理机制以及能够研究室温下更大尺度的器件结构，2011年，Dong等人在铁磁双交换模型的基础上构建了微观量子模型，系统研究了磁性铁电氧化物异质结中的界面磁电耦合与电阻开关效应[30]。研究表明铁电场效应可以导致与之耦合的磁性薄膜中巡游电子浓度的变化，从而改变薄膜的物理属性，导致界面处的磁性相变。由于铁电场效应只能穿透锰氧化物2∼3个晶格长度，如图21(d)所示，因此常规铁电–锰氧化物异质结的总体电控磁效果很微弱。为了进一步提高电控磁的效率，Dong等人又设计了可以实现完全电控磁开关的双层锰氧化物多铁器件模型[180]，如图21(e)所示。该超晶格是由铁电材料BaTiO3层以及磁性材料LSMO双层构成，由于存在极性界面，较多的电子（空穴）占据n(p)型界面侧的Mn层，这种电荷分布的不均匀性可以通过铁电极化来控制。Dong等人通过紧束缚模型和密度泛函理论研究发现，通过改变铁电极化方向，可以调控锰氧化物双层在铁磁相和亚铁磁相之间转换，总磁矩变化的调控幅度达到90%以上，且可以在较高温度下工作。

在物理机制上，基于铁电场效应的磁电耦合形式可以表示为(∇·P)M2。从该磁电耦合形式可以看出，磁电耦合效应只能调节M的大小，不能调节M的方向（M2项的限制）。因此尽管上述锰氧化物双层模型的开关比很高，M的大小可以实现相当大的调制，但是M的方向依旧不能翻转。此外，磁相转变在实验上很难控制，因为它要求体系必须处于可调控的相变边界附近。同时，当锰氧化物层数很薄的时候，磁性层的 “dead layer” 问题也备受争议[99,106,181−185]。因此要实现室温下的磁电耦合效应，尤其是电控磁回线（E−M回线），仍需进一步探索。

2016年，Weng等人基于铁电场效应，提出了一种新型的磁电耦合机制，即 (∇·P)(M·L)[186]。该新型磁电耦合机制不依赖于磁相变，且可以实现电场控制bmM方向的 180度翻转。其关键之处在于用(M·L)项来替换上述的M2项，式中L是反铁磁序。如果反铁磁序L很稳固，就可以通过极化P的翻转来调控M方向的翻转，实现电控磁翻转及电场–磁化回线，这是磁电材料研究的重要功能性目标。

图21.铁电场效应示意图：(a)极化向上在界面处吸引空穴；(b)极化向下在界面处吸引电子；取自 [180]。(c)PZT/LSMO超晶格对外电场的磁响应，取自[178]；(d)eg电子密度分布n(z)和静电势V(z)；取自[30]；(e)双层锰氧化物多铁器件模型，取自[180]

一般而言，场效应(∇·P)是具有层状依赖性的，也就是说层状的反铁磁序 (如A型反铁磁序)会和场效应有很好的耦合效应[180,187]。然而具有层状A型反铁磁的材料很少，尽管一些锰氧化物 (如 LaMnO3和 Nd0.5Sr0.5MnO3)会呈现出 A型反铁磁序[29,45]，但都非常脆弱，在薄膜中很难体现出来[55,57,95]。实际上，赝立方钙钛矿材料中最常见的反铁磁序是G型反铁磁，如图22(a)所示。若沿着赝立方 [111]方向观察，这种G型反铁磁序就是层状排布的，如图22(b)所示。因而[111]取向可以将无法与铁电场效应耦合的 G型反铁磁旋转成可以与铁电场效应耦合的层状反铁磁。基于此，我们设计了沿 [111]方向[38]生长的(BiFeO3)m/(SrTiO3)n异质结来实现上面提出的新型磁电耦合机制，如图22(c)所示。

以双层 BiFeO3（包含三层 Bi离子和两层 Fe离子）为例，由于三层Bi3+离子的结构会使得体系引入一个额外的电子，且被限制在Fe双分子层中，随着铁电极化的翻转，Fe双分子层的电子占据态将会发生变化，产生Fe2+-Fe3+或Fe3+-Fe2+的电荷有序态。如图22(e)所示，当极化P向上时 (Pup)，Fe1的轨道额外占据一个电子，从Fe3+变成Fe2+，呈现出dxy轨道或dyz轨道形状，而 Fe2依旧保持 Fe3+状态，整个电子云分布几乎是个球形。与此相反，当极化P向下时 (Pdown)，Fe2的轨道额外占据一个电子，从Fe3+变成Fe2+，而Fe1依旧保持Fe3+状态。由于Fe离子之间是反铁磁耦合，所以极化方向翻转的时候，BiFeO3双层的净磁矩M将在−1µB和+1µB之间进行切换。研究发现，上述电控磁矩方向翻转只有在Bi层和Fe层处于非化学计量比的情况下（体系才能引入一个额外的电子或者空穴）才能实现，如图22(f)所示。事实上，实验中即使Bi和Fe的层数一样（如2+2情况），但是一旦存在O空位或者Bi空位，就会引起非化学计量比，上述的磁电耦合功能依旧可以实现。

图22.(a)从[001]方向观察的 G型反铁磁铁示意图；(b)从 [111]方向观察的 G型反铁磁示意图；(c)[111]取向的BiFeO3/SrTiO3超晶格，包含三层Bi和两层Fe；(d)体系可能的极化方向，a表示极化方向与(111)面的夹角；(e)超晶格中BiFeO3层电子云的空间分布：Pup和Pdown；(f)超晶格中不同层数BiFeO3对应的磁电耦合效应，其中非零的净磁矩M 可以被电场调控；取自[186]

BiFeO3块材有八个沿[111]取向的极化方向，而在沿[111]方向生长的BiFeO3/SrTiO3超晶格中，这八个极化方向P可以分成两组：(1)极化P的方向和 [111]面垂直（两个状态：α=+90◦/−90◦）；(2)极化P的方向和 [111]面有一定的夹角（六个状态：α=+19.47◦/−19.47◦），如图22(d)所示，这两组极化方向的电控磁调控结果一样。极化P调控M翻转的完整过程如图23所示，其中E−M回线就是我们所迫切追求的磁电功能。此外，BiFeO3优异的铁电性能和鲁棒的磁性保证了电控磁功能可以在室温工作 [160,188]。

图23.(a)能量 vs极化 P示意图；(b)电控磁示意图：随着极化P方向的翻转，M 的方向也相应的发生翻转。矫顽力由 BiFeO3层的矫顽力决定，最大饱和磁矩 |M|可以达到 0.5µB/Fe；取自 [186]

实际上，在钙钛矿超晶格中，还有许多其它物理效应可以实现磁电耦合，比如应变效应、隧穿磁致电阻效应、阻变效应等[189−195]。如此丰富的磁电耦合效应为实现低功耗、高密度、快速读写的多铁器件提供了更多可能性。

VI.总结和展望

本综述简要介绍了钙钛矿超晶格中的磁电物性，对超晶格中的磁性调控、铁电性调控以及磁电耦合三个方面进行了总结和讨论。如上所述，钙钛矿超晶格因其强关联电子特性，蕴含了丰富的物性，既具有很高的基础研究价值，也为多功能器件的开发提供了素材。然而伴随着实验技术和理论机制的逐渐发展和完善，研究过程中必将会不断涌现出新的物理现象和问题，需要我们进一步的研究和探索：

(1)过去对钙钛矿超晶格的研究主要集中在3d过渡金属氧化物，而对于包含4d/5d过渡金属的钙钛矿超晶格研究相对较少。相比3d轨道，4d/5d轨道电子具有较强的自旋轨道耦合作用，因此其物性具备很多新奇的特点，例如稳定磁拓扑相、增强磁晶各项异性等。目前已经有理论和实验工作开始将目光投向了包含 4d/5d过渡金属的超晶格[196−200]。

(2)电子铁电性如今正吸引着越来越多的研究者的关注，然而过去对电荷有序态的研究主要集中在钙钛矿锰氧化物中，而对其他过渡金属化合物的关注相对较少，因此在有限的材料范围内实现基于电荷有序的磁电耦合效应相对困难。将电子铁电性拓展到其他过渡金属氧化物，甚至拓展到过渡金属氟化物，这将为探索更高性能的磁电材料提供帮助。

致 谢

本文综述的研究工作是与Elbio Dagotto教授、姚裕贵教授、黄欣博士、林玲芳博士合作完成，特此感谢。