基于ANSYS的输电导线找形方法研究与分析

陈昌隆 ，陈佳昊 ，张晨晟 ，王佳伟

（合肥工业大学宣城校区建筑工程系，安徽 宣城 242000）

0 前言

随着我国电力事业的快速发展，输电塔和输电线路的数量不断增加，而输电线路在气温、风力的外界因素作用下会发生舞动、脱冰跳跃及短路电流和电晕引起的振动，这严重威胁了输电塔及架空线的安全[1]。输电导线一般采用金具绝缘子串张拉或悬挂于相邻2座输电塔之间，有着极强的几何非线性，是一种典型的柔性悬索结构，没有抗弯抗压能力，抗剪切能力也很弱，导线的形态与预加张拉力有关[2]。输电导线找形分析就是确定输电导线在自重或外荷载作用下的平衡位置形态和应力分布,是输电线路微风振动、覆冰舞动、脱冰跳跃等动力分析的基础和前提,找形结果的精确程度直接影响着后续动力分析的准确性[3]。因此有效的导线找形是输电设计的理论依据，也为输电线路的安全分析提供了基础。

目前基于ANSYS的输电导线找形主要有直接迭代法和找形分析法[4]，这2种方法在ANSYS中通过逐步施加重力荷载获取导线形态，不能反映在施工中导线形态的形成过程，故本文基于输电导线架设中牵引放线的过程对输电导线找形采用一种新的方法即滑移加载法。在两塔间按导线长度建立模型，对导线施加初应变、重力加速度和牵引拉力，通过不断增大牵引拉力使节点滑移，从而模拟导线牵引放线过程，当节点移动到输电塔悬挂导线处，即可得到导线重力作用下的初始形态。ANSYS软件具有较强的非线性处理能力，是目前进行非线性结构有限元分析中使用最为广泛的软件之一[2]。因此，结合现场施工技术研究输电导线找形在ANSYS上的实现更有现实意义。

1 输电导线找形方法

1.1 输电导线找形原理

由于架空输电线路的档距比架空线的截面尺寸大得多，同时架空线的刚性对其悬挂空间曲线形状的影响很小；据此可以假定架空线是没有刚性的柔性索链，只能承受拉力而不能承受弯矩，其次假定作用在架空线上的荷载沿其线长均匀分布。根据这2个假设，悬挂在两基杆塔间的架空线呈悬链线形状，根据悬链线公式可得图1情况下输电导线方程[5]为:

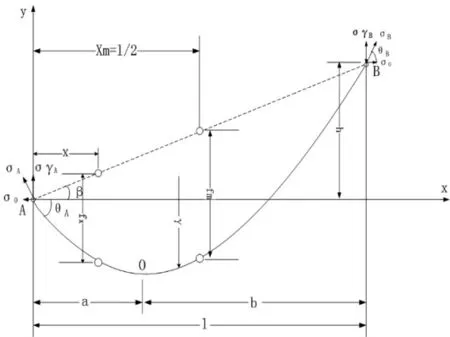
图1 输电导线初始形态

根据弧垂的定义，不等高悬点架空线任一点处的弧垂为：

在己知架空线最低点处轴向应力时，架空线上任一点的轴向应力可以表示为：

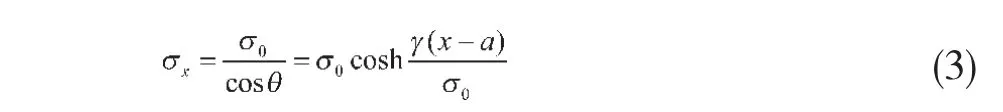
输电导线整档线长为：

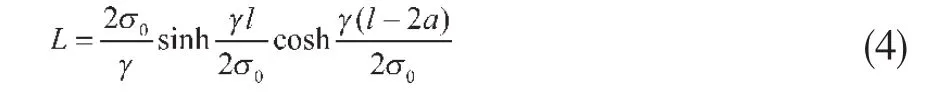
1.2 有限元法找形方法

1.2.1 直接迭代法。

在弦线位置创建模型，设定单元类型及材料性质，并设置很小的初应变；施加约束和自重荷载，并进行网格划分形成有限元模型；求解并逐步更新有限元模型，以导线水平张力或节点位移为收敛条件进行迭代，其最终结果即为导线在自重荷载作用下的初始形态[6]。

1.2.2 找形分析法

在弦线位置创建模型，选择单元类型，设置较小的弹性模量和较大的初应变，生成有限元模型；施加荷载和约束后求解，更新有限元模型后，恢复材料真实弹性模量并设置较小初应变；采用类似直接迭代法的方式进行平衡迭代，更新有限元模型即可得到自重荷载作用下导线形态[6]。

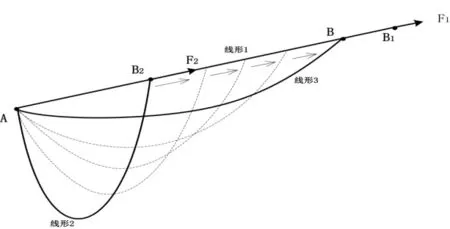
图2 滑移加载法示意图

1.2.3 滑移加载法

在找形过程中，除了预张拉力能稍微改变线长，线长本身是不会改的;在考虑线长时，在预张拉力的作用下初始形态的线长和找形后的导线线长相等。如图2所示初始时将导线一端在悬挂点A处固定，另一端沿输电导线弦线AB方向拉至B1处,AB1的长度等于输电导线的线长，即得初始模型为线形1；导线在重力作用滑动至B2，施加拉力将节点B2拉到B点处被固定，此时档距间的导线呈悬链线形状，即得自重荷载作用下导线形态。

1.3 滑移加载法在ANSYS中的实现

输电线路导线是悬索结构的一种，在初应力和重力的作用下，输电导线的形态理论上是悬链线形；最大弧垂由导线的竖向比载和导线弧垂最低点处的水平应力决定[8]。由于输电导线只能受拉不能受压的特性，所以在ANSYS中采用LINK10单元模拟输电导线[9]。

下面仍以图2来说明滑移加载的操作步骤。

①创建几何模型和有限元模型：在AB处方向上建立模型AB1，AB1长度为档距间导线的线长，选择LINK10单元模拟输电导线,并设置材料性质及很小的初应变，划分网格形成有限模型。

②施加约束及荷载：在A点处施加完全约束，在B1点处通过旋转节点坐标系对B1施加不完全约束，使节点B1可在AB方向上滑动，对模型施加重力加速度和AB方向上较小的拉力F1。

③求解：打开几何非线性（NLGEOM,ON）和应力刚度(SSTIF,ON)选项进行求解，更新有限元模型，模型到达较低位置线形2处，施加较大张力F2，不断增大F2并更新模型，以水平张力或位移为收敛条件进行平衡迭代，最终得到线形3即为输电导线在重力作用下的形态。

2 算例分析

导线参数 表1

本文分别使用解析法和有限元法对算例进行计算分析，并对找形结果数据进行分析比较。以某档不等高悬点架空输电导线为例，档l=120m，高差为h=20m，导线物理参数见表1[10]。

图3中各方法所得最低点处的水平张力与实际值误差均小于0.1%，可认为计算收敛，所得结果即为ANSYS中在重力作用下输电导线的找形形态。

根据悬链线公式计算出理论上输电导线的部分节点弧垂、线长及最大张力，同时提取不同有限元法的找形结果，将两者列于表2、3中进行误差分析和比较。表2中n1为直接迭代法与解析法间的误差，平均值为0.392%；n2为找形分析法与解析法间的误差，平均值为0.436%；n3为滑移加载法与解析法间的误差，平均值为0.202%。表2和表3中n1的平均值为0.341%，n2的平均值为 0.392%，n3的平均值为0.229%，所得误差均小于2.5%，满足工程需要[11]。图4为滑移加载法与解析法找形结果比较，由图可知两者几乎重合，说明了滑移加载法的精确性和有效性，可以替代悬链线法应用于工程实际中。

3 总结

本文介绍了输电导线的解析法找形、直接迭代法和找形分析法找形，提出了滑移加载法，并通过具体算例将不同找形方法所得结果进行比较分析，得出以下结论：

图3 找形结果图

①三种基于ANSYS的有限元找形方法所得结果与理论值的绝对误差很小，满足工程需求，验证了有限元找形的有效性和准确性。

②在相同的网格数量下，由误差平均值可知滑移加载法的误差小于直接迭代法和找形分析法（0.229%＜0.341%＜0.392%），说明相同情况下滑移加载法更能准确地反映输电导线的形态。

③本文所提的滑移加载法是在输电塔线施工基础上模拟牵引导线的过程，较其他方法而言，更贴近现实，为其他悬索、导线的找形提供新的思路和方法。

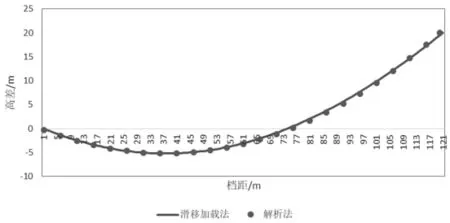
图4 结果对比图

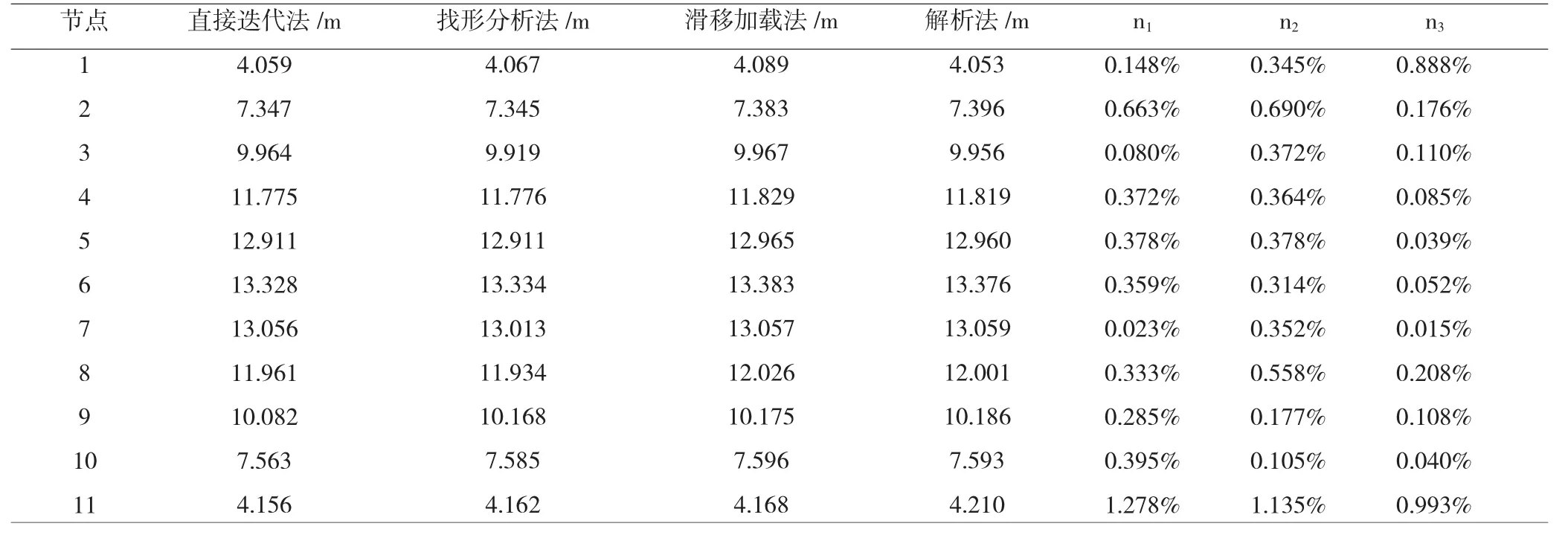
弧垂结果对比 表2

线长及最大张力结果对比 表3