多点锚泊定位系统布锚夹角的影响及优化分析

韩森，贾宝柱，孙文正，顾一鸣

大连海事大学轮机工程学院，辽宁大连116026

0 引 言

为避免海洋钻井平台在受到环境扰动后发生位置漂移，需要配备能保证其在允许范围内变化的定位装置，如动力定位或锚泊定位系统，以确保其满足作业条件要求。其中，锚泊定位系统具有装备成本低、系统结构简单、控制方便等优点，被广泛应用于水深不超过450 m的海洋浮式结构物。

近年来，随着合成材料及定位控制技术的发展，锚泊定位也作为深水平台的辅助定位方式，与动力定位一起构成复合定位系统［1］。对在开敞水域内作业的半潜式钻井平台，对其位置的控制精度要求相对较高，常采用4点、8点甚至是12点的多点布锚方式。多数平台具有轴对称形状，作业过程中艏向和侧向受到的环境扰动力差别较小，因此，在进行辐射状布缆时可不考虑作业区域及环境力的差别因素，通常采用对称形式的锚索布设方法。系统中，若假设锚泊线的预紧力为定值，则在布锚时希望能最大限度地提高用于保持平台水平位置的作用力，这就需要对锚泊系统的悬链线进行合理安排。理论计算及实际工程经验表明，通过改善锚泊线的悬垂形状及优化同一组锚链线之间的夹角，能够提高系统的定位能力。韩森等［2-5］对采取加装浮子或沉子方式改变锚泊定位系统的悬链线悬垂形状以提高平台定位的能力进行了研究。Qiao等［6］对2种静力特性和布锚方式相同而锚泊线组成不同的锚泊系统进行了非线性时域耦合分析，并研究了两者系泊线张力的差异。Guo等［7］分别借助准静态方法和动态方法，研究了水下悬浮隧道（Submerged Floating Tunnel，SFT）的运动幅度和频率随锚泊线参数变化时对平台回复力的影响，结果表明，与准静态方法相比，动态方法得到的回复力约高出30%。对于多点锚泊定位系统，可以通过优化同一组悬链线之间的夹角来增强系统抵抗外界环境扰动的能力。Shafieefar等［8］使用遗传算法对锚泊系统进行了优化设计，并详细给出了解决优化问题的流程，其优化目标包括平台艏向、锚泊系统布设（包括锚的位置及锚泊线夹角）以及锚泊线材质的组成，结果证明，锚的位置及锚泊线夹角会对平台抵抗扰动的能力产生较大影响。金鸿章等［9］使用改进的遗传算法对锚链张力进行了优化，改进的方法包括增加自适应算法以加强其局部搜索能力，以及采用基于收缩系统的种群生成方法来增加初始种群的精英程度。余龙等［10-11］通过准静定法研究了不同锚泊线组成对锚泊系统静回复力的影响，并建立优化模型求解得出了锚泊线的最优组成。严传续等［12-13］分析了铺管船锚泊定位系统的结构和受力，并通过优化算法对锚固点位置及锚泊线受力进行了优化，可使铺管船满足作业要求。目前，针对锚泊定位系统的优化主要集中在锚泊线组成优化以及浮子位置和浮力大小的优化方面，鲜有针对布锚夹角对锚泊系统定位性能影响及优化的研究。

本文拟通过分析布锚夹角对静回复力、锚泊线受力均匀程度以及平台转角的影响，来对传统遗传算法的初始种群生成方法进行改进。遗传算法拥有较好的全局搜索能力，且鲁棒性以及计算时效性好，但传统的遗传算法局部搜索能力差，容易陷入局部最优解。而通过结合自适应算法，则可提高其局部搜索能力，进而提高布锚夹角的优化精度，增强锚泊定位系统对外部扰动的抵抗能力。

1 静回复力计算

1.1 建立模型

以平台中心为坐标原点，水平方向中线为x轴（艏向为x轴正向），纵向中线为y轴（左舷为y轴正向），建立海洋平台船体坐标系。平台采用8点对称式布锚，锚泊线编号为1～8，示意图如图1所示。其中，虚线为平台受到环境扰动后的位置。

图1 锚泊系统示意图Fig.1 The schematic diagram of mooring system

图1 中，编号分别为 W1，W2，W3，W4的 4 台锚绞机布置在平台的4个角上，每台锚绞机控制2条锚泊线，其夹角为θ，相邻锚绞机之间的距离分别为x0和y0。若平台位置变化后其中心由o点移动到o′点，直线位移大小为δm，则北东坐标系（NE）下的移动方位角为β。因采用的是非汇交锚泊系统，在平台位置变化后其艏向会发生改变，设艏向角度变化量为ψ。根据绕轴转动公式，可建立平台锚绞机在北东坐标系下的新坐标方程：

式中：sgn为符号函数；XWi，YWi分别为第i台锚绞机 Wi的横坐标和纵坐标值，i=1，2，3，4。

定义平台位移后锚泊线的水平长度与其初始状态下的水平长度之差为等效位移ΔL，则

式中：Xk，Yk分别为与第k根锚泊线连接的锚在NE坐标系下的横坐标和纵坐标，其中i=1，2，3，4，k=1，2，…，8，锚绞机和锚泊线存在对应关系，例如W1对应L1和L2，以此类推；L为锚泊线在预张状态下的水平长度。

当锚固点不变时，锚绞机的等效位移ΔL即为相应锚泊线长度的变化。假设8根锚泊线的材质及组成完全一致，因为锚泊线顶端水平张力与位移呈现非线性关系，故无法用统一的数学方程描述，不过可以采用级数对其进行逼近。设锚泊线顶端水平张力T与等效位移的关系为：

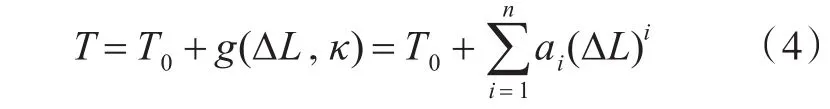
式中：T0为锚泊线在预张力状态下的水平分力；κ为锚泊线顶端张力与海平面的夹角，其值与ΔL满足函数关系；ai为待求参数；n的大小与单根锚泊线的应力模型有关。

已知锚泊线顶端水平张力与等效位移的关系函数，可以求出锚泊线水平张力T，其与NE坐标系中E轴的夹角为λ：

已知锚泊线顶端的水平张力T及夹角λ，通过力的合成，可求出锚泊系统的静回复力F为

式中：Tk和λk分别为第k根锚泊线提供的水平张力及作用方向。

设M为艏摇方向的平台力矩，则

式中：d为锚绞机至平台中心的距离；μi为锚绞机Wi与平台中心的连线和船体坐标系下x轴的夹角。

图2 求解流程图Fig.2 Solution flow chart

1.2 求解方法

在已知平台位移的情况下，求解静回复力F及平台艏向角度变化量ψ。当布锚夹角θ以及锚泊线的材质组成确定后，通过建立的NE坐标系，得到预张力状态下的锚绞机及锚固点坐标。已知平台位移，并假设一个平台艏向变化量为ψ，通过式（1）和式（2），可求出平台位移后的锚绞机坐标，进而通过式（3）得到所有锚泊线的等效位移ΔL。将等效位移ΔL代入锚泊线顶端水平张力—位移的函数式（4）中，就能求出每根锚泊线顶端的张力T，最后，经过力的合成求出平台的静回复力F，具体计算流程如图2所示。

2 水平张力与位移函数的确定

对锚泊线顶端的水平张力进行计算时，首先要确定式（4）中的待求参数。以三段式组合锚泊线为研究对象，上段锚链与锚绞机相连，中段为钢缆，下段锚链与锚相连。在钢缆中串联浮子以改善锚泊系统的静力特性［14］，并考虑其尺度作用。海洋平台的工作水深为300 m，海流的切向和法向阻力系数分别为0.024和1.2［15］，流速分布为均匀流1.2 m/s。将整串浮子的起点位置安置在距锚泊线顶端550 m处，浮子和锚链的直径为等效直径，相关参数如表1所示。

表1 锚泊线的性能参数Table 1 The performance parameters of mooring lines

在锚泊线顶端施加预紧力能使平台在一定的扰动下正常作业而不需要锚绞机运行，选择合适的预紧力能够增强锚泊系统抵抗扰动的能力［16］。

对锚泊系统的所有锚泊线预加某初始张力，使平台处于平衡位置，当外载荷作用于平台时，平台会发生位移。在锚绞机不动作的情况下，锚泊系统迎风面的锚泊线中总有一根的受力最大。以受力最大的锚泊线为研究对象，当平台处于允许的作业半径时，此锚泊线刚好达到安全应力的临界点，这时的初始锚泊线张力即为最佳预紧力。

本文中锚泊线采用的安全系数为2。通常规定平台的工作半径为水深的3%～5%，本文将平台的允许作业半径设为12.123 m。以锚泊线顶端位移为x轴，锚泊线顶端张力为y轴，建立平面直角坐标系。当锚泊线顶端位移为12.123 m，顶端张力刚好处于安全应力的临界点（2 920 875 N）时，其张力—位移曲线与x=0的交点即为锚泊线的最佳预紧力。根据给出的锚泊线参数，使用分段外推法在Matlab软件中搭建锚泊线的应力模型，得出单根锚泊线顶端张力与位移的关系曲线如图3所示。

图3 锚泊线的张力—位移曲线Fig.3 The tension-movement curve of mooring line

由图3可知，锚泊线的最佳初始预紧力为1.5×106N。

继续使用搭建的锚泊线应力模型，得出单根锚泊线水平张力与位移的关系，并对式（4）中的参数进行求解，得到锚泊线顶端水平张力与等效位移的函数关系为

所得函数图形与通过仿真得到的锚泊线顶端水平张力和位移关系点的差异如图4所示。

由图4中可以看出，函数曲线较好地反映了锚泊线水平张力与位移的关系，式（8）可以用于锚泊系统静回复力的计算。

图4 锚泊线的水平张力—位移曲线Fig.4 The horizontal tension-movement curve of mooring line

3 影响分析

3.1 静回复力的影响

锚泊系统的定位能力由所有分布在平台四周的锚泊线共同决定，本节将通过给出的锚泊系统静回复力计算方法，在Matlab软件中搭建锚泊系统静回复力计算模型，研究不同的布锚方式对静回复力大小的影响。当海洋平台在扰动的影响下处于允许作业半径时，锚泊系统所能提供的静回复力越大，说明平台抵抗外载荷的能力越强，锚绞机动作的频率越小，锚泊系统的定位性能越好。本文采用对称式布锚，因为流速对锚泊线的偏移量几乎没有影响，故只研究在位移方向β=0～π/2 rad范围内，布锚夹角在允许作业半径上对静回复力的影响，如图5所示。

图5 布锚夹角对静回复力的影响Fig.5 Influence of mooring angles on static restoring force

由图5可以看出，当布锚夹角θ＜0.8 rad时，静回复力随平台位移方向的增大是先减小后增大，即平台对介于艏向和侧向之间的扰动的抵抗能力较弱；当布锚夹角θ＞0.8 rad时，静回复力随平台位移方向的增大是先增大后减小，即平台对艏向和侧向的扰动抵抗能力较差；当布锚夹角θ在0.8 rad附近时，静回复力随平台位移方向的增大变化很小，此时平台对扰动作用的方向不敏感。当布锚夹角θ=0 rad、平台位移方向为0 rad时，锚泊系统在允许作业半径上提供的静回复力值最大，为4.6×106N；当布锚夹角θ=0 rad、平台位移方向为0.8 rad时，锚泊系统在允许作业半径上提供的静回复力值最小，为4.49×106N，两者相差较大。

3.2 锚泊线受力均匀性的影响

对布锚夹角的确定，不能单单只考虑平台对扰动方向的敏感程度以及锚泊系统在允许作业半径上的静回复力大小，也要考虑单根锚泊线的受力，特别是锚泊线受力的均匀程度。锚泊线在扰动的影响下受力越均匀，则锚泊线发生断裂的可能性就越低。用8根锚泊线受力的标准差表示锚泊线受力的均匀程度，当平台位于允许作业半径时，布锚夹角对锚泊线受力均匀程度的影响如图6所示。

图6 布锚夹角对锚泊线受力均匀程度的影响Fig.6 Influence of mooring angles on tension uniformity of all mooring lines

由图6可以看出，当布锚夹角θ＜0.8 rad时，锚泊线在各个位移方向的受力都很均匀；而当布锚夹角θ＞0.8 rad时，锚泊线受力的均匀程度随平台位移方向的增大是先减小后增大。当布锚夹角θ=π/2 rad、平台位移方向为π/2 rad时，锚泊线在允许作业半径上的受力最不均匀，8根锚泊线的受力标准差为8.63×105N；当布锚夹角θ=0 rad、平台位移方向为0 rad时，锚泊线在允许作业半径上的受力最均匀，受力标准差为8.59×105N，两者差距不大，可见不同的布锚方式对锚泊线受力的均匀程度影响不大。

3.3 平台艏向的影响

锚泊系统的锚泊线并不相交于一点，因此平台在扰动的影响下既发生位移，又发生转动。下面，将研究布锚夹角在各个位移方向对平台艏向变化量ψ的影响，如图7所示。

图7 布锚夹角对平台艏向的影响Fig.7 Influence of mooring angles on heading of platform

由图7可以看出，平台在任意位移方向上其艏向变化都会随布锚夹角的增大而减小，即增大布锚夹角，能抑制平台受扰动后的艏向转动。平台在0～π/2 rad范围内的艏向变化均为正值，即平台转动方向全部为逆时针。当布锚夹角θ=0 rad、平台位移方向为0.8 rad时，平台在允许作业半径上的艏向转动最大，为1.56×10-2rad，可以忽略不计。

4 布锚夹角的优化

由于布锚夹角对平台艏向的影响可忽略不计，因此对布锚夹角进行优化时只需考虑3种因素：静回复力大小F、静回复力对扰动方向的敏感程度S和锚泊线的受力均匀程度E。优化的目的是使平台在允许作业半径上的静回复力大，对方向的敏感程度低，各锚泊线受力均匀。以此建立目标函数：

约束条件为：

式中：P为锚泊系统的性能；F值用各个位移方向上的静回复力平均值表示；S值用各个位移方向上的静回复力标准差表示；E值用各个方向上锚泊线受力标准差的平均值表示；位移方向的离散精度为0.001，所以N值为1 570；下标j表示平台的位移方向是j/N；下标k为锚泊线的编号。因为F，S，E的单位都是牛顿，因此不需要进行无量纲化。

为解决传统遗传算法局部搜索能力差、容易陷入局部最优解的缺点，本文对遗传算法（GA）进行了改进：一是利用之前给出的仿真分析，人为地生成初始种群，确保初始种群的精英程度；二是通过自适应算法，改变交叉和变异概率，进而提高遗传算法的局部搜索能力。

根据之前的仿真结论，当θ在0.8 rad附近时，静回复力对方向的敏感程度最低；θ越接近0 rad，锚泊线的受力越均匀。设种群数目popSize=10，为保证初始种群具备一定的精度且多样性较强，令初始种群为｛0 0.05 0.2 0.5 0.75 0.8 0.85 1 1.3 π/2｝。

在进化中，以适应度的变化来改变交叉和变异的概率。设群体的最佳适应值为gmax，当代的最佳适应值为fmax，当代的平均适应值为favg；设定2个交叉概率和2个变异概率，分别为Pcmax，Pcmin和Pmmax，Pmmin。具体的算法如下。

如果g＞K，

否则，

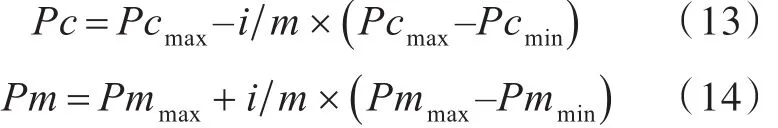
式中：g为fmax与gmax的比值；K为设定的阈值；i为进化代数；m为总的进化代数。

遗传算法的最大进化代数为200，K=0.9，Pcmax=0.8，Pcmin=0.6，Pmmax=0.04，Pmmin=0.02，自变量离散精度eps=0.001。将建立的静回复力模型导入改进的遗传算法中，分别采用传统GA和改进GA对布锚夹角进行优化，结果差异如图8所示。

图8 两种优化方法进程Fig.8 The optimization process of two methods

优化结果表明，改进的遗传算法拥有更快的收敛速度以及更高的优化精度，因此更适合作为布锚夹角的优化算法，通过仿真得到的布锚夹角θ=0.795 rad。

布锚夹角确定后，即可得出各根锚泊线在允许作业半径上的受力。根据受力最大的锚泊线，在保证其他参数不变的情况下降低其破坏强度，进而降低锚泊系统的制造成本。由于本文只研究平台0～π/2 rad方向内的位移，所以只研究3～6号锚泊线在允许作业半径上的受力，如图9所示。

图9 锚泊线受力图Fig.9 The tension of mooring lines

锚泊线在允许作业半径上的最大张力为2 870 401 N，安全系数为2，则锚泊线的破坏强度可降低到5 740 802 N。

5 结 语

本文提出了一种锚泊系统静回复力的计算方法，给出了求解流程，并使用此方法研究了布锚夹角对平台静回复力、锚泊线受力均匀程度以及平台艏向角度的影响。结果表明，当布锚夹角θ在0.8 rad附近时，平台对扰动的方向敏感度最低；当布锚夹角θ较小时，锚泊线的受力更加均匀；增大布锚夹角θ能抑制平台受扰动后的转动，但影响很小。在布锚夹角优化方面，根据影响锚泊定位系统性能的3种因素建立目标函数，并利用改进的遗传算法进行了优化。优化结果表明，改进的遗传算法具有较好的收敛速度及优化精度，最优布锚夹角θ=0.795 rad。最后，将优化后的布锚夹角反馈给锚泊系统受力模型，研究了锚泊线在允许作业半径上的受力，最终将锚泊线对材质破坏强度的要求降低到了5 740 802 N。