融合对分课堂和微课视频的智能控制课程教学案例设计

尹 钟，陈 玮，付东翔，傅迎华

（上海理工大学 光电信息与计算机工程学院，上海 200093）

0 引 言

智能控制课程是智能科学与技术本科专业的核心课程之一，与迅速发展的人工智能技术密切相关[1]。该课程通过引入机器学习、模糊推理系统、数据挖掘等最新方法，为蕴含不确定、非线性、时变等特性的被控对象提供了可行的建模方法。为了帮助学生透彻理解智能控制方法涉及的知识难点，授课教师需要在实际教学环节灵活运用新型教学技术、互联网资源和多媒体教学工具，融合复数教学方法，同时结合自身研究方向最新专业知识，提升备课效率和授课质量[2]。

“对分课堂”是复旦大学张学新于2014年提出的一种结合传统讲授和深入讨论的非传统授课方式[3]，该方式将教学过程依据时间划分为讲授、内化吸收和讨论3个环节。其核心理念是将一半课堂时间分配于教师讲授，另一半分配于学生以讨论形式进行交互式学习。智能控制课程内容频繁涉及线性代数、概率论、最优化方法等抽象数学理论，数学基础的差异性可能导致学生难以在有限反应时间内稳定地跟踪讲授过程的逻辑思路。因此，引入对分课堂方法所提出的学生与学生、教师与学生之间的讨论环节，可帮助学生在教师的引导下更好地巩固所学知识点。

另一方面，针对智能控制课程讲授环节中的一些概念非常抽象，难以通过有限的教学设备具体地向学生展示其原理机制。此时，可以利用“微课”方法制作5分钟左右的教学视频，实现有明确的教学目标，内容短小，集中说明一个问题的子课程[4]。在录制视频过程中，可预先利用相关软件，以动画形式具体展现抽象知识点的机制和功能。微课视频可无缝融入对分课堂的讲授环节中，从而将授课环节转化为口授与微课、内化吸收、深入讨论等3个新的环节。综上，笔者的动机在于通过引入对分课堂的交互式讨论环节和微课视频的抽象知识可视化功能，提高学生的课堂注意力，降低学生的认知负荷，优化教师的授课质量。最终，笔者在以往教学和科研工作的启发下[5]，设计了一组面向多元教学模式的智能控制课程教学案例。

1 融合对分课堂和微课视频的教学模式结构

为了实现对分课堂和微课视频教学技术的融合教学模式，首先需要重新确定讲授与讨论环节的时间比重；其次，需要识别智能控制课程中的哪些知识点需要利用微课视频辅助授课；最后，为了验证新教学模式的有效性，需要在教学案例实施过程中对学生认知负荷进行评估，分析该模式是否有利于学生吸收和掌握知识难点。针对以上3点，在案例中笔者将口授、微课、讨论的时间权重分别设置为60%、10%、30%，平缓地从传统授课模式过渡至对分—微课融合模式。与此同时，结合智能控制课程的教学大纲和相关专业知识，笔者系统分析了每个知识点的理解难易度，并以“支持向量回归建模”知识点为例设计了教学案例。此外，引入NASA-TLX（NASA Task Load Index）指标评估融合对分课堂与微课视频授课模式下学生的学习压力。案例对应的教学模式结构如图1所示。

图1 融合对分课堂和微课视频的教学模式结构图

2 教学案例设计

以智能控制建模中常用的支持向量回归方法为基础，笔者分别设计涵盖了课堂讲授、微课视频、对分课堂讨论环节和上机实验4个方面的教学案例（见表1）。这些案例将帮助学生循序渐进地掌握支持向量机建模方法，并深入理解过拟合现象对模型性能的影响。

2.1 课堂讲授案例

案例1：对简单数据的支持向量回归建模。

该案例通过传统讲授和幻灯片的形式帮助学生了解支持向量机及其回归模型的基本数学原理。案例1包括4个主要模块。

（1）统计学习过程的一致性。最大间隔分类原则是经典支持向量机分类模型的重要机制。为了帮助学生理解该机制的必要性，教师首先使学生领会经验风险（训练误差）并不能总是一致地反映模型的期望风险（测试误差）。

（2）凸最优化问题最优性条件。鉴于支持向量机优化模型为典型的带约束条件的凸最优化问题，此处先引入凸集、凸函数等相关概念，再阐述求解凸函数最小值的最优性条件——梯度向量为零，最后回顾拉格朗日乘子法的基本原理，导出优化模型的求解方法。

（3）基于数据驱动的回归建模。由于支持向量回归模型与分类模型既有相似性又有区别，教师此处需要讲解并举例说明回归问题的一般概念，及其在智能控制领域中的重要作用（例如系统辨识等）。

（4）支持向量回归。基于模块（1）详细讲解支持向量回归方法的基本优化模型，继而基于模块（2）阐明其求解算法，最后利用（3）引入并讲解核函数和超参数概念。上述4个模块对应的知识点结构如图2所示。

2.2 微课视频案例

案例2：分析不同超参数对模型性能的影响。

学生通过对案例1的学习可发现支持向量回归模型的泛化能力与超参数的选择密切相关。为了进一步使学生形象地理解超参数变化与模型拟合能力的关系，笔者录制了一份微课视频——结合动画、字幕、讲解——向学生展示支持向量回归模型的训练结果。

表1 围绕支持向量回归建模知识点的教学案例设计

图2 课堂讲授案例内含的教学模块及其知识结构

首先，π确定核函数类型为高斯径向基核函数，通过视频按照图3中的素材逐步演示随着缩小正则化参数（图中的gamma）和高斯核宽度参数（图中的sigma2）后，模型对训练样例的拟合结果。训练数据集通过函数y（k）=sin［πx（k）］/［πx（k）］+v（k）人工生成，其中，v（k）为对第k个样例施加的服从正态分布的噪声项。学生通过对比图3中的（a）、（b）子图即可发现选择合适的超参数使支持向量回归模型与真实函数更加接近。反之，则可能出现模型过分追求高训练精度而导致过拟合。

图3 微课视频案例的支向量回归建模动画演示素材

2.3 讨论环节和上机实验案例

案例3：不同数据驱动建模方法存在的过拟合问题。

依据对分课堂模式，围绕案例1、2中的支持向量回归建模问题和过拟合现象，在第2周授课引入讨论环节。该环节首先将3～4位学生分为一组，同时布置3个讨论议题：①神经网络回归问题是否会出现类似的过拟合现象？②过拟合现象与训练集和回归模型的哪些性质密切相关？③如何避免过拟合？讨论环节之后，每组学生派选1位代表阐述议题结论，最后再由教师总结。

案例4：支持向量回归方法的具体实现。

学生通过案例1、2、3的学习，可在掌握支持向量回归训练算法的同时，更加深入地理解基于数据驱动建模的注意事项。在此基础上，引入一个实验课案例，要求学生通过查阅资料编写支持向量回归的Matlab程序，该程序需要引入3个子程序：①带约束凸函数最优化问题求解函数，获取解拉格朗日乘子；②模型参数计算函数，通过拉格乘子确定超平面法向量和截距；③模型测试函数，计算测试样例的估计输出。综上，通过上述循序渐进的4个教学案例，可帮助学生更加牢固地掌握如图2所示的知识结构。

3 教学实施

依据上述4个教学案例，笔者设计了相应教学模块，并将其实施于上海理工大学智能科学与技术专业本科三年级学生的智能控制课程中。为了部署对分课堂，按照学号将每3～4名学生分配于一个小组，并调整座位，继而开始授课环节。微课视频可利用doceri、完全演示、汇思等相关平台制作。比较推荐的策略是利用开放的MOOCs教学资源，获取精彩的智能控制知识点讲解案例。

教学实施结束后，委托学生填写了12份基于NASA-TLX指标的主观评价量表，用以评价传统授课模式与新模式的教学效果差异。该指标要求学生对每个模式包含的6个方面（包括脑力需求、身体负担、时间需求、任务绩效、努力程度、挫败感）分别评分（0～100分，分数越高对应程度越高）。表2以均值和标准差的形式对比了两种教学模式下学生的认知负荷。其中，脑力需求表征学生在听课和教学互动环节的认知资源消耗，由表2可知，新教学模式下平均脑力需求指标更高，说明该模式能引导学生注意力进一步集中。另一方面，新教学模式引发的身体负担相对传统教学模式更低，因此学生在授课结束后疲劳水平更低。新教学模式对应更高的时间需求指标，该现象说明对分课堂的讨论环节给学生带来了更大的时间压力和紧迫感。任务绩效和努力程度指标表征学生在授课结束后对听课效果的主观感受，可见，新教学模式下授课效果得到一定程度提高。特别在新教学模式下，学生的平均挫败感更低，说明对分课堂和微课视频环节能较好地帮助学生理解关键知识点。

值得指出，新教学模式下的努力程度指标提升较小，其潜在原因包括：①对分课堂的议题难度过高或过低，可能导致学生参与讨论的意愿存在差异，这一缺陷可通过课后反馈逐步修正议题的范围和复杂度得到改进；②由于微课视频环节占用时间设置不当，可能导致讲授环节对知识点剖析深度不够以及对分课堂环节讨论不充分。该缺陷可通过微调上述3个模块的时间比率得到缓解。以此为基础，未来我们将逐步改进现有的教学实施范式，进一步提高新教学模式的授课效果。

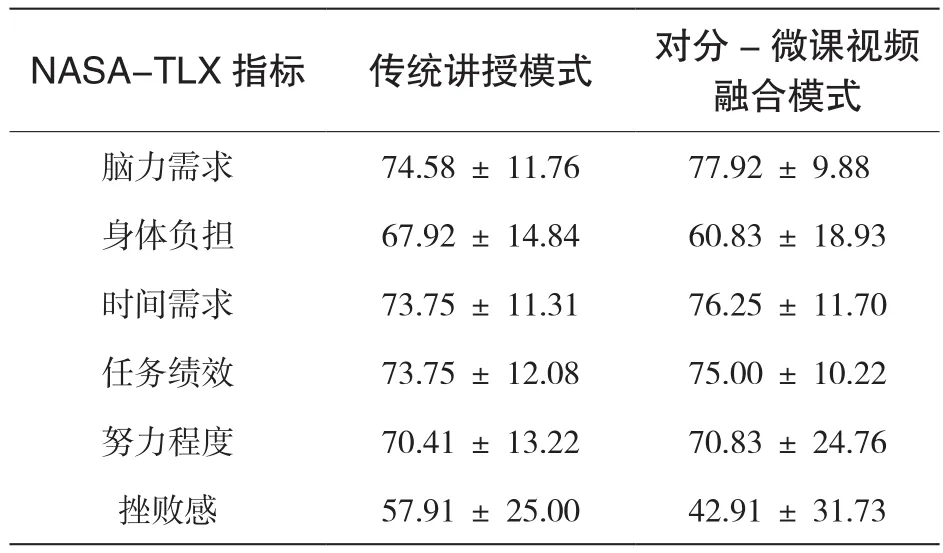
表2 基于NASA-TLX指标的两种教学模式下学生认知负荷对比

4 结 语

针对当前高校学生学习热情不高、课堂注意力难以长时间集中、纯口授方法教学效率有限的主要问题，笔者通过结合对分课堂和微课视频教学技术，设计了循序渐进的4个教学案例，调动学生学习智能控制方向课程的积极性。在降低学习过程脑力负荷的同时，提高学生的学习效率。通过引入认知负荷统计量表，笔者发现学生在新案例授课模式下听课效果更佳。在未来工作中，可引入更丰富的微课视频教学资源，进一步提高对分课堂授课方法的部署效率。同时，更谨慎地验证该混合授课模式能否显著提高学生在智能科学与技术相关课程的学习效果。