“电磁场与电磁波”教学中物理模型的构建方法和作用研究

兰俊卿，杜国宏

（成都信息工程大学，四川 成都 610225）

1 物理模型的概念

物理模型是指人们借助特定物理场景，对复杂实际问题进行抽象化处理，得出的一种能形象反映问题本质特性的现象、过程或结构模型等[1]。人们通过学习和研究物理模型，了解原型客体特性及其运动和变化规律。在教学过程中，合理构建物理模型既可以帮助学生以更加直观、形象的方式来分析和研究问题，又可以加深学生对于知识的理解，让学生了解知识的潜在应用价值，从而从根本上提升学生分析和解决物理问题的能力[2-3]。

“电磁场与电磁波”是工科电类专业必修的一门基础理论课。学生通过本门课程的学习，可以掌握电磁场和电磁波的基本概念和基本理论，同时为后续相关专业课程学习奠定基础。但是通过多年教学发现，在课程教学过程中存在诸多问题。

1.1 课程内容抽象

在课程学习过程中，学生耗费大量时间研究复杂的数学推导和进行枯燥的解析求解。学生无法为电磁场和电磁波构建形象化的物理模型，不能从根本上认识电磁场的存在形式和变化规律。

1.2 课程中包含大量的理论推导

需要用到先前学到的数学知识。但是在数学课程中，重点是放在数学分析上，没有为数学定义构建形象化的物理模型，无法认识到相关数学知识点的物理应用。因此，在“电磁场与电磁波”中使用相关数学知识的时候，学生难以理解数学公式所代表的物理意义。

1.3 课程重点是理论知识

课程无法有效提升学生们分析和解决电磁场问题的能力，同时也无法激发学生的学习兴趣，这样不仅不利于后续相关课程的开展，也无法从根本上提升学生的能力[4]。

为了有效解决以上问题，本文提出，在课程讲授中应该重视物理模型在整个教学中的作用。面对复杂抽象的电磁场问题，首先，要合理选择物理场景，建立让学生容易理解、能够反映物理问题本质属性的物理模型。其次，为课程中常用的、抽象的数学知识构建数学物理模型，重在让学生了解数学知识背后潜在的物理应用。最后，在物理模型的基础上，通过分析物理过程可以帮助学生更加客观地认识和理解物理现象的本质。更重要的是，可以培养学生严谨的逻辑分析能力，从根本上提升学生分析和解决物理问题的能力。本文将通过对以上3点内容进行详细阐述，来探究物理模型的构建方法和作用。

2 合理选择物理场景，反映物理问题本质

首先，在构建物理模型的时候，由于学生的知识背景和理解能力不尽相同，所以新构建的物理模型必须要简单、易懂。其次，新构建的物理模型不应该拘泥于电磁场这门学科，应该将学生引入熟悉的物理场景，或者生活中经常遇到的以及学生们感兴趣的事情上。这样不仅可以帮助学生们以更加简单的方式来理解抽象的电磁现象，还能激发学生的学习兴趣。最后，物理模型一定要具备反映原物理问题本质特性的功能。本文将通过“均匀平面波”概念的讲解来探讨以上内容。

“均匀平面波”是电磁波的一种理想情况，作为最简单的电磁波传播形式，是学习和研究电磁波的基础，在“电磁场与电磁波”课程教学中占有重要的地位。由于电磁波是看不见、摸不着的，在教学过程中，如何让学生理解均匀平面波的传播特性就成为课程讲授的最大难点。本文将通过引入新颖的物理场景，为学生构建能够反映均匀平面波传播特性的物理模型。

首先，在物理场景的选择上，本研究突破了电磁场这门学科的束缚。我们选择通过抽动拔河所用的麻绳所产生的“振动波”来构建均匀平面波物理模型。这样将同学们的思维从复杂的电磁场模式转换到拔河场上。因为绝大多数同学都参与过拔河比赛，可以较容易地联想到，当上下抽动麻绳一端时，麻绳会产生半圆弧状“突起”，突起会沿着麻绳传播。为了简化模型，我们假设绳子无限长，同时假设每次抽动都是相同的，并且突起在传播过程中没有能量损耗。这样就借助麻绳建立起一个典型的“振动波”传播模型。即每抽动一下绳子，就会有一个特定半圆弧形状“突起”产生并沿着绳子一直传播下去。

其次，在构建了物理场景之后，将引入“波阵面”的概念。波阵面是空间相位相同的点构成的曲面。为了让同学们理解什么是相位相同的点，构建如图1所示的振动波模型。

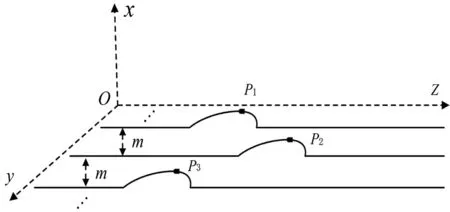
图1 振动波模型

如图1所示，在yoz平面上，每间隔m距离放置一根麻绳，绳子平行于z轴。在不同的时间分别抽动每一根麻绳左端点。经过一段时间t后，呈现如图所示的情况。所谓“相位相同点”就是图1中麻绳“突起”上相对位置相同的点（例如图1中所示p1，p2和p3是3个突起的峰值点，就是一组相位相同的点）。当绳间距m减小的时候，在y方向，相同距离就可以放置更多的麻绳。当m趋于0的时候，在yoz平面上就可以放置无数根麻绳（绳子粗细忽略不计）。我们把每个突起的相位相同点连起来就构成了一条曲线。这个时候我们可以把这条曲线叫作“波阵线”。上面研究的情况是集中在yoz二维平面上，将上述情况沿着z轴扩展到三维，把垂直于z轴的每个平面上的“波阵线”进行连接就构成了一个曲面，这个曲面就是“波阵面”。

知道了波阵面的概念之后，假设抽动绳子的时间是相同的，那么这个时候上述模型中的波阵线就是平行于y轴的一条直线，那么波阵面就是一个平面。所谓“平面波”就是指当波阵面是平面时的情况。这里我们研究的场量是振幅。假设每次抽动绳子的状态都是相同的，在平面波上，任一点上绳子的振幅状态都是相同的，所以任意点上振幅和（x，y）坐标没有关系。这种情况下，我们就可以把这个平面波叫作“均匀平面波”。

通过上述实例，我们选择“拔河”作为物理场景，通过构建由拔河绳产生的“振动波模型”来讲解均匀平面波。虽然振动波和电磁波有本质上的不同，但是对于“均匀平面波”的概念来说，却没有本质的区别。同学们通过学习由振动波构建的平面波模型容易理解相位相同点、波阵面、平面波等均匀平面波概念中的难点。更重要的是，同学们可以为自己构建出一个清晰的“平面波模型”。

3 数学物理模型构建方法

在构建数学物理模型的时候，不仅应该重视数学推导，更应加强对于数学知识潜在物理应用的学习。本文提出通过引入物理模型，让学生理解数学知识背后潜在的物理应用。

在电磁场理论学习中，“梯度”是描述电磁场的重要数学概念。教学实践证明虽然在数学课上，同学们已经学习过梯度，但是很多同学认为梯度概念抽象，不清楚梯度可能的物理应用在哪里。本文将通过构建“梯度”物理模型，研究数学物理模型的构建方法和意义。

首先，本文将以“爬山”作为物理场景，在如图2所示的理想圆柱状山峰中构建标量场的等值面模型。

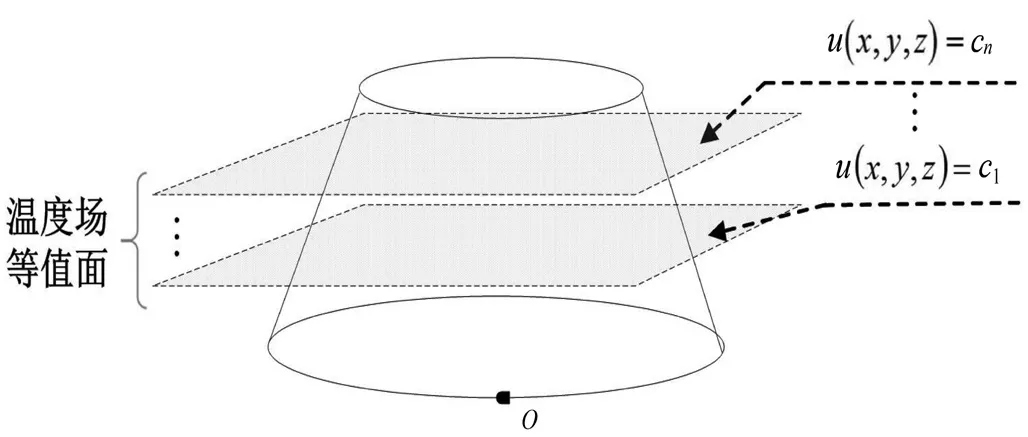
图2 温度场等值面模型

由于温度是标量，所以山峰间温度场可以表示为：

所谓“标量场的等值面”就是指标量函数取得相同数值的点时形成的一个空间曲面。所以图3中，温度场的等值面就是函数u取得相同数值的点时得到的曲面，即：

为了简化模型，本文假设温度只和山峰的高度有关，那么温度就可以表示为：

如图2所示，温度场的等值面就是垂直于z轴的平面。

其次，将在图2温度等值面模型的基础上引入“方向导数”概念。爬山是大多数同学都亲身实践过的一项户外活动。在爬山的时候，尤其是遇到高度落差较大的山峰时候，会感觉到随着高度的变化，温度会出现明显的下降（理论上平均每上升100 m，温度会下降0.6 ℃），如图3所示。

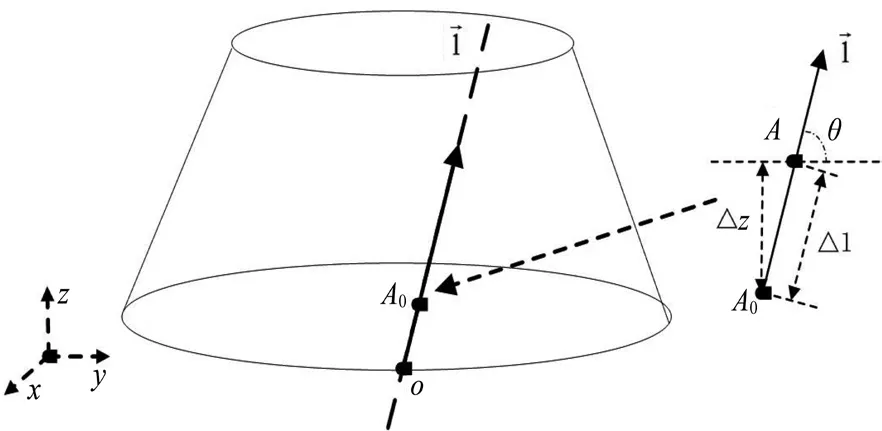
图3 方向导数模型

经过点A0时温度瞬间变化率可以表示为：

式（5）就是标量温度场u在点A处沿着l 方向的方向导

0数。通过上述讲解同学们就可以为方向导数建立起一个非常清晰的对应物理模型。即在行进的过程中某点，沿着行进方向上，温度随路程的变化率。

最后，建立“梯度”的物理模型。为了简化模型，假设温度场u随z轴呈线性变化，即：

这里的“-”号指的是温度降低。 那么如图3所示，A0点的方向导数就可以表示为：

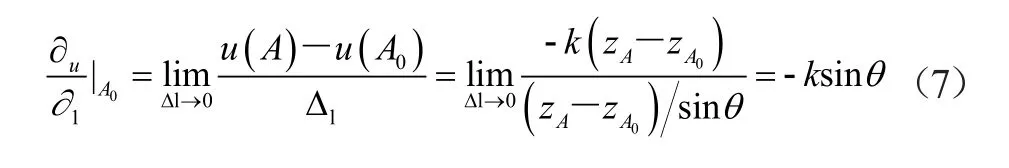
其中θ为前行方向和y轴正方向之间的夹角。由式（7）可知，A0点的方向导数与sinθ成正比。并且当θ等于90°的时候，方向导数的绝对值取得最大值。

在此基础上，引入梯度的概念。标量场u中某点的梯度是一个矢量，它的大小等于该点最大方向导数的值，它的方向指的是最大方向导数所指的方向。以图3所示模型为例，温度场中A0点的梯度的方向就是θ等于90°的时候，大小等于-k。

通过上述讲解，我们将复杂、抽象的数学概念应用到了同学们熟悉的物理场景里。同学们借助数学物理模型的帮助不仅可以学习数学概念的本质，更重要的是同学们知道了数学概念的物理应用，为今后使用该数学知识奠定了重要的基础。

4 基于物理模型的“物理过程”分析方法

在物理知识的讲授过程中，加强对于“物理过程”的分析不仅可以帮助学生更加客观地认识和理解物理现象的本质，更重要的是，可以培养学生严谨的逻辑分析能力，从根本上提升学生分析和解决物理问题的能力。本文提出借助物理模型培养学生“物理过程”的分析能力。下面将以第三部分“方向导数”的物理模型为例，探究基于物理模型的“物理过程”分析方法。

首先，本文提出将“物理过程”的分析凝练在一个学生熟悉的场景或者故事中。在方向导数的讲授过程中，我们以图3中山峰温度场模型为基础，将物理过程的分析转变成研究在爬山过程中温度随路程的变化率。这样可以使学生能够“身临其境”的感受物理现象的变化，在“亲身实践”中培养学生的物理过程分析能力。

其次，借助物理模型，通过“提问”引导学生合理推演和分析物理过程，在分析中学习物理现象的本质和变化规律。在学习方向导数概念的时候，我们首先给大家抛出一个问题：“是否在爬山的时候感受到过温度的变化？”通过问题引导大家进入“爬山状态”，并和老师一同感受爬山过程中温度的变化。这个问题在一定程度上还可以帮助大家较深刻地记住梯度研究的对象是标量场。在此基础上我们构建图3理想温度等值面模型，然后让学生分析，在爬山过程中，如果选择不同的路径或方向爬山，感受到的温度随路程变化率会怎样。同学们借助图3温度等值面模型，可以直观地想象出行进方向会影响到温度随路程的变化率。

上述分析可以让帮助同学直观地理解方向导数的物理意义。同时通过上述方法，同学们在问题的引导下，对物理过程进行合理推演，并通过分析爬山过程中温度的变化，学习和掌握方向导数的概念和物理意义，这样可以有效地培养学生逻辑分析能力，从根本上提升分析和解决物理问题的能力。

5 结语

本文针对“电磁场与电磁波”教学中存在的问题，提出重视物理模型在整个教学中的作用，通过合理选择物理场景，构建反映物理问题本质的物理模型，将抽象、复杂的电磁场直观地展现在同学们面前。同时，为课程中较抽象的数学知识构建数学物理模型，重在让学生了解数学知识背后潜在的物理应用。最后，借助物理模型，突出对“物理过程”的分析，通过分析物理过程帮助学生更加客观地认识和理解物理现象的本质，学习运动和变化规律。更重要的是可以培养学生严谨的逻辑分析能力，从根本上提升学生分析和解决物理问题的能力。希望本文可以为“电磁场与电磁波”课程的教学工作提供新的方法和思路。