基于MDP随机路径模拟的电动汽车充电负荷时空分布预测
张 谦, 王 众, 谭维玉, 刘桦臻, 李 晨
(输配电装备及系统安全与新技术国家重点实验室(重庆大学), 重庆市 400044)
0 引言
随着世界能源结构调整与汽车工业技术发展,电动汽车(electric vehicle,EV)是新能源汽车的主要发展方向。大规模电动汽车接入,将给电力系统规划和运行带来不可忽视的影响,包括负荷增长[1]、影响电能质量[2]、电网运行优化控制难度增加[3]、对新型配电网规划提出新的要求等[4]。解决以上问题的基础是实现对电动汽车充电负荷时空分布的有效预测,故迫切需要建立准确有效的负荷预测模型。
国内外学者对电动汽车充电负荷预测开展了广泛的研究。文献[5]分析了计程车、公交车、私家车等的充电特点,采用蒙特卡洛方法预测了中国未来电动汽车的充电总负荷,建立起了充电需求的统计学概率模型。在此基础上,研究人员进一步考虑了用户日行驶里程[6-7]、充电起始时间[8]、出发回家时间[9-10]等随机变量对充电负荷的影响。文献[11]将每辆参与调度的电动汽车作为移动社交网络(MSN)平台中的单一个体,考虑到其影响力,研究了在分时电价约束下的电动汽车充放电行为预测方法,但未考虑到电动汽车的空间分布问题。文献[12-15]将区域划分为工业区、商业区、住宅区等,按照各个区域不同的充电特性计算充电负荷的时空分布,由于对电动汽车的空间分配是预先确定的,该方法没有模拟出电动汽车因随机移动而产生的负荷时空分布。文献[16]利用电动汽车大数据,分析电动汽车的可能充电时间和位置,并结合电池、交通、出行需求和充电习惯等约束,计算电动汽车负荷的时空分布,但是目前整合多平台的大数据仍有较大的困难。文献[17-18]采用最短路径算法模拟了电动汽车的空间行驶分布,进而建立充电负荷的时空分布,但没有考虑到驾驶者路径选择的随机性。文献[19]利用O-D矩阵反推法和云模型建立起充电负荷时空分布预测方法,但屏蔽了路网的物理结构,无法考虑电动汽车在行驶过程中需要充电的情况,也忽略了环境温度对负荷的影响。文献[20]构造出行链模型,对五大出行区域建立了时空分布模型,使用模糊数学方法计及了温度与交通对电动汽车能耗的影响,但没有具体到每一条道路的交通状况与每个时刻点的温度情况。
综合来看,目前对电动汽车充电负荷时空分布预测存在两个问题:一方面对电动汽车空间行驶路径模拟多采用最短路径算法,该方法对驾驶者驾车随机性考虑不足,文献[21-22]的研究表明不同驾驶者基于道路拥堵状况、出行时长、出行距离、道路等级、道路熟悉程度等的不同,在最短路径的目标下会做出相对不同的路径选择,即具有随机性。并且电动汽车按照固定路线行驶,将导致相同起始点的电动汽车总是在固定的充电站充电,地块划分法与O-D反推法也存在同样的问题;另一方面交通拥堵状况与天气状况对电动汽车的能耗有着显著影响,电动汽车在怠速与频繁启停的状况下耗电量增加超过25%,而空调的开启导致能耗增高20%以上[23]。目前对电动汽车时空分布研究中常忽略该问题,或对其计量不够精确。
针对上述两个问题,本文计及实时交通与温度,提出了一种基于马尔可夫决策过程随机路径模拟的城市电动汽车充电负荷时空分布预测方法,首先根据各类车型充电方式与出行特点对各类电动汽车进行分类;其次基于蒙特卡洛方法,结合出行链建立各类电动汽车的时空转移模型,采用马尔可夫决策理论,以行驶时间最短为目标,考虑路径选择的随机性和实时交通状况,进行实时动态路径模拟;根据电动汽车实测数据建立温度、交通能耗模型,计算实时单位里程耗电量,结合电动汽车充电条件、行驶路径,计算电动汽车充电负荷的时空分布。最后以某典型城区为例,验证了该方法的有效性。本文假设各节点电动汽车充电设施能够充分满足电动汽车充电需求。
1 电动汽车时空转移模型
1.1 电动汽车分类
本文主要考虑日常市区内出行需求,电动汽车电池容量在30 kW·h左右,城市居民市区通勤总里程均值约为30 km[24],折算耗电量约为5 kW·h。为了分析快充和慢充两种不同的充电需求对充电负荷预测结果的影响,从充电方式与出行特点出发,将电动汽车分为以下几种类型。
私家车:工作日往返于工作地与居住地,休息日外出休闲,含A和B两类车。
公务车:工作日往返于各工作地,休息日不出行,含A和B两类车。
计程车:一天中出行多次,行驶目的地随机, 每日运行,仅含B类车。
其中A类车指具有固定慢充设备的电动汽车,以夜间在其停车位慢速充电满足电能需求。B类车指不具有固定慢充设备的电动汽车,当剩余电量较低时在途经地进行快速充电,其能量补充方式与汽油车加油方式类似。
1.2 各类电动汽车出行模型
1.2.1私家车与公务车
私家车与公务车出行地点具有典型的目的性,可以用出行链描述。出行目的可分为家(H)、工作(W)、购物用餐(SE)、社交娱乐(SR)和其他事务(O)共5个类型,这些出行目的地同时也是电动汽车充电场所[25]。本文中涉及的出行链如附录A图A1所示。工作日,私家车活动行程为H-W,H-W-SR/SE/O,H-W+H-SR/SE/O,记为行程1,2,3。非工作日活动行程为H-SR/SE/O,分为上午出发与下午出发两类,记为行程4,5。公务车活动行程为W-W和W-SR/SE/O,记为行程6,7。各活动行程所占比例设定如附录A表A1所示[25-26]。
根据车辆类型与工作与否,对应各活动行程所占比例,每辆车出行链服从式(1)的概率分布。
(1)
式中:C为出行链;Ps和Pg分别为私家车与公务车的出行链概率分布;pi为各行程概率。
每段行程的开始时刻服从正态概率分布,其概率密度函数[5]如式(2)所示。
(2)
式中:ts为行程开始时刻;μ和σ分别为开始时刻均值与方差,不同出行链对应不同数值。
将所有电动私家车或公务车视为总体,每一辆车视为一个二维随机变量,其联合分布函数为:
P(C∩ts)=P(C)P(C|ts)
(3)
对于式(3),通过蒙特卡洛模拟的方式抽取出行链类型与出发时间。
1.2.2计程车
每日00:00时,计程车从所属的计程车公司出发,开始接受订单,行驶到客户所在地,再前往客户出行的目的地,抵达之后再接受新的订单,如此循环。在每日23:00之后停止接受订单,回到所属公司所在地交班[23],如附录A图A2所示。
1.3 基于马尔可夫决策理论的电动汽车随机路径模拟
1.3.1马尔可夫决策值函数向后递归算法
一个马尔可夫决策过程由一个五元组M=(T,S,A(i),p(j|i,α),R(i,α))构成,其中T为决策时刻集,表示选取行动的时间点集;S为状态集,表示在每个决策时刻,系统状态空间集;A(i)为行动集,表示在任一决策时刻,决策者观察到的状态是i∈S,在状态i选取的可用行动集;p(j|i,α)为状态转移概率,表示在状态i下,采取行动α转移到状态j的概率;R(i,α)为回报函数,表示状态i下,采取行动α后,决策者获得的回报。
马尔可夫决策动态过程如下:决策者在T(0)时刻所在状态s(0),从A(0)中选择一个动作α(0)执行,执行后按P(s(1)|s(0),α(0))概率随机转移到了下一个s(1)状态。再执行一个动作α(1),依次向后,直到最后时刻T(N),到达最终状态s(N),如附录A图A3所示。
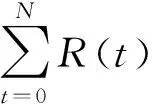
(4)
式中:st为t时刻所处状态,t=0对应初始状态s(0),以递归形式表示为
Vπ=R(s(i),π)+
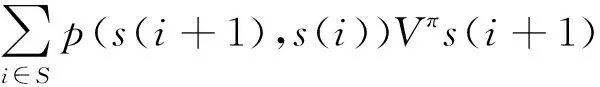
(5)
对每个策略π,其对应的值函数Vπ是一系列线性方程的唯一公共解。式(5)称为Bellman公式,最优策略可以通过基于动态规划的期望报酬值向后递归的方法得到[27]。
1.3.2针对电动汽车路径模拟
若将电动汽车行驶的各路径长度视作回报函数R,则马尔可夫决策描述的路径选择过程是一种实时动态的路径选择过程。向后递归计算最优策略满足Bellman最优化原理,即电动汽车行驶过一个路段进行下一次路径选择都是在该实时状态下以当前所在节点为起点,以最短行驶距离(时间)为目标进行路径选择。并且路径选择行为具有随机性,引入随机概率因子γ来描述这种随机性,具体模拟方法如下。
采用图论方法将电动汽车行驶路网抽象为有向图。将负荷预测区域内所有节点集合视为状态集S,从电动汽车起点到终点行驶经过每个节点的时刻视为决策时刻t,在每个节点决定行驶的下一条路径视为行动a,将要行驶的路径长度视为回报R。
以图1中4节点区域为例:状态集S={1,2,3,4},行动集A={a,b,c,d};R(a)=65 m,R(b)=95 m,R(c)=90 m,R(d)=97 m,π1={a,b},π2={c,d},设1为起点,4为终点,则
(6)
定义行动状态转移矩阵P,表示采取某行动后电动汽车在各状态之间转移的概率。若行动a,b,c,d均为全概率转移,即以概率1转移到下一状态,以行动a为例,则P矩阵表示为:
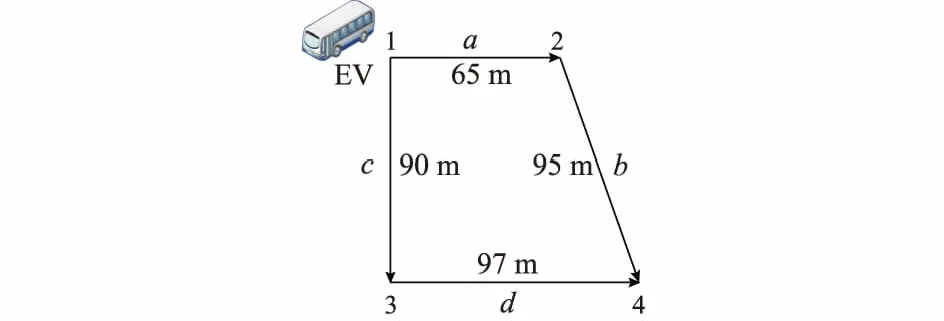
图1 马尔可夫决策4节点示意图Fig.1 Schematic diagram of 4-node Markov decision

(7)
当电动汽车位于节点1时,执行动作a将以概率1转移到节点2,处在其他节点时则以概率1保持位置不变。此时最优策略为最短路径,即π1={a,b}。
实际电动汽车在行驶中以部分概率转移模式行驶,引入(0,0.5)间服从均匀分布的随机概率因子γ描述驾驶者决策的随机性,γ值小于0.5保证每一个节点的路径选择多数情况是实时最短路径,即实时最短路径选择概率较大。当电动汽车驾驶者执行某行动时,有概率γ转移到另一条路径。对上例中行动a而言,其行动概率转移矩阵为:
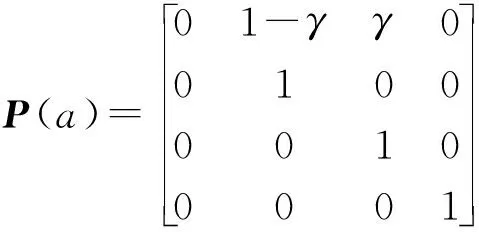
(8)
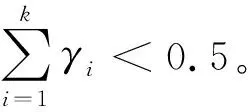
不同的概率因子对应不同的最优策略,γ的引入将路径选择中最优路径与随机性相结合。对于区域内的每一辆电动汽车,已知其起讫点后,设各道路长度为Li,根据2.1.1节中各道路等级与实时交通状况,得到t时刻各道路的行驶速度Vi,t,将各边权值设定为通过各边所需时间Ti,t,则有Ti,t=Li/Vi,t。将带随机概率因子马尔可夫决策过程(MDP)算法中回报函数R数值设置为Ti,t,以向后递归的方法计算路径,不同的交通情况将会产生不同的路径选择。对应汽车所处路段的Vi,t,可以得到私家车各时刻所处位置。
2 电动汽车充电负荷计算
2.1 单位里程耗电量
电动汽车单位里程耗电量影响因素有很多,其中交通与温度状况对其影响最大[28]。不同的交通状况下行驶速度不同,单位能耗不同。温度过高或过低会导致驾驶员开启空调,增加电动汽车能耗,影响电动汽车充电负荷的时空分布。
2.1.1交通能耗模型
《城市道路工程设计规范》将城市道路分为4个等级,每种等级的道路在不同拥堵情况下具有不同的行驶速度,如附录A表A2所示。文献[29]基于电动汽车实测数据建模,得到对应于实时拥堵情况下的单位里程耗电量,如式(9)所示。
(9)
式中:Eksl,Ezgl,Ecgl,Ezl分别为快速路、主干路、次干路、支路的单位里程耗电量;V为电动汽车速度。若t时刻x位置上电动汽车速度为V(t,x),式(9)中单位里程耗电量可表示为El(t,V(t,x)),下标l代表各道路等级。
2.1.2温度能耗模型
文献[30]研究了不同温度区间下的汽车空调开启率,对文献数据处理后拟合出空调开启率计算式(10)。文献[28]定义温度能耗比例系数,即空调开启后不同温度对应的单位里程耗电量与空调关闭条件下耗电量之比,处理实测数据得到拟合公式见式(11)。
Kpect=k1U3+k2U2+k3U+c1
(10)
Ktemp=k4(U+c2)2+c3
(11)
式中:U为气温(摄氏度);Kpect为空调开启率;Ktemp为温度能耗比例系数;k1~k4和c1~c3为拟合参数,函数图像如附录A图A4所示。空调未开启时,温度变化对单位能耗影响较小[26],故忽略不计。
2.1.3统一表示
综合交通、温度的影响,实时单位里程耗电量可用式(12)表示:
(12)
2.2 各类车充电负荷计算方法
1)A类私家车、公务车。A类私家车与A类公务车均为固定地点慢充模式,采用相同的方法进行充电负荷计算。A类车充电方式为每天回到停车位进行慢充,充电时长可表示为式(13),时间变量关系可表示为式(14)。
(13)
Te=Ts+Tc
(14)
式中:Tc为充电时长;Pc为充电功率;L(x)为途经路段长度;Te为充电结束时刻,设置为充满电池时刻;Ts为充电开始时刻,设置为抵达停车位时刻,由时空转移模型可得。
2)B类私家车、公务车。B类私家车与B类公务车均为途经地快充模式,采用相同的方法进行充电负荷计算。电池剩余电量D(t)可由式(15)计算。
D(t)=D1-∑L1(x)E1(t,x)
(15)
式中:D1,L1(x),E1(t,x)分别为上一次充电结束后的剩余电量、已行驶过路段长度和单位里程耗电量。
若电池剩电量不足以到达下一个目的地,即满足式(16)条件,则电动汽车在当前地点立即进行一次快速充电,直到电池充满,充电时长可表示为式(17)。
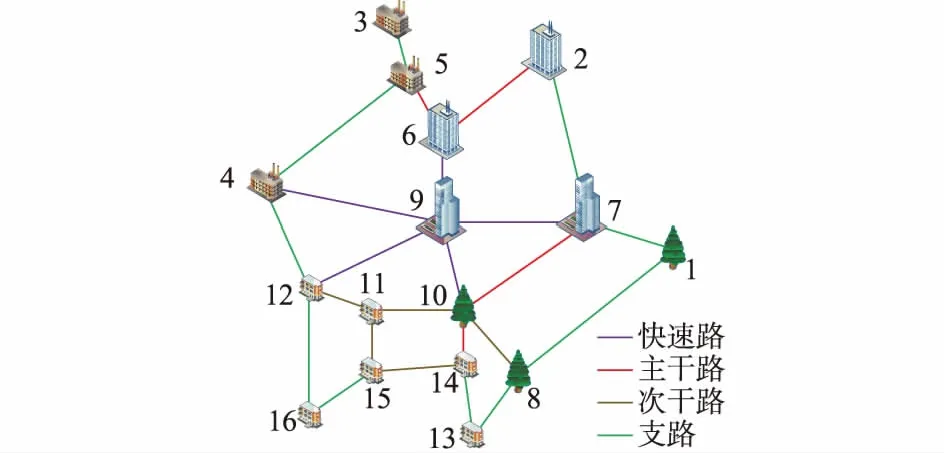
D(t) (16) (17) 式中:L0(x)和E0(t,x)分别为当前要行驶路段的长度与单位里程耗电量;Dfull为电池满电状态电量。 3)计程车。由于其送客需求不能在行程中进行充电,设置充电条件为一段行程结束后剩余电量小于30%,即D(t)<30%,则在该地点立即进行一次快速充电,直到电池充满,充电时长同式(17)。 得到每辆车的充电开始时间与充电时长后,考虑到快充车辆多为“几天一充”方式,因此以一周7天为时间单元。若仿真时间为K周,第k类电动汽车中第i辆于每周t时刻在m节点充电的概率可以表示为: (18) 因此对于节点m而言,一周内t时刻其充电负荷的期望可以表示为: (19) 以某典型城区为例,将路网中并行道路合并,抽象为图2所示的含16个节点、20条边的交通网络图。其中各边所带颜色代表其道路等级;节点11至16为居民区(H);节点2至6为工商业区(W);节点1,7,8,9,10为娱乐购物休闲区(SR/SE/O)。根据国家发展和改革委员会印发的《电动汽车充电基础设施发展指南》对城市充电设施的设置建议,6个H地点和5个W地点同时具有快充桩和慢充桩,5个SR/SE/O地点设置快充桩。 图2 某典型城区交通网络图Fig.2 Traffic network diagram of a typical urban area 仿真区域各道路长度如附录A图A5所示,设置各类电动汽车数量如附录A表A3所示[21],模拟大规模电动汽车入网。各类车型出行链相关数据设定如附录A表A4至表A11所示。私家车、计程车与公务车一般为小型车,以长安逸动电动汽车为标准,电池容量30 kW·h,慢充功率7 kW,快充功率25 kW,即A类车充电功率为7 kW,B类车与计程车充电功率为25 kW。定义典型周为气温25 ℃左右,交通状况良好的一周。定义高温周为气温超过35 ℃,其他条件与典型周相同的一周。拥堵周为上下班高峰期交通严重拥堵,其他条件与典型周相同的一周。典型周与拥堵周相关温度与拥堵状况如附录A表A12和表A13所示。仿真开始时刻假设所有电动汽车电池荷电状态(SOC)为100%。设置仿真步长为1 min,仿真时间为600周。本文建立的计及实时交通与温度的电动汽车充电负荷时空分布预测模型使用MATLAB软件进行仿真,仿真流程如附录A图A6所示。 1)MDP随机路径模拟与最短路模拟 对从节点2到节点16的路径采用MDP随机路径模拟与最短路径模拟(Dijkstra算法)各10次,前4次结果如附录A图A7所示,实线为MDP算法路径,虚线为Dijkstra算法路径,10次路径模拟编号如附录A表A14所示。结果表明,由于最优策略为期望总距离(时长)最小的路径,因此总长越短的路径被选择的概率相对越高。MDP算法能够避免最短路径算法中相同始终点电动汽车在固定地点充电的问题,体现电动汽车用户在行驶中空间移动的随机性,更符合实际充电需求。 2)典型周下电动汽车充电总负荷 典型周下电动汽车充电总负荷如附录A图A8所示,仿真结果表明,对于同时具有快充和慢充能力的节点,如节点11至16,充电负荷以一周为周期来看走势相对平缓、峰谷差率较小。主要承担快充功能的节点,如节点1,7,8,9,10,充电负荷波动次数较多,峰谷差率较高,08:00—22:00平均峰谷差率超过75%,最高超过90%,其中枢纽节点9负荷波动情况最严重。部分节点典型周一天负荷波动情况如图3所示。 图3 部分节点典型周一天负荷波动情况Fig.3 Load fluctuations of some nodes for one day in a typical week 3)高温周下电动汽车充电负荷 将典型周与高温周节点10充电负荷进行横向比较,如图4所示。仿真结果表明,一周内持续高温会导致节点充电负荷峰值持续时间增加,较典型周平均每天增加约2.5 h。 图4 节点10典型周、高温周充电负荷曲线Fig.4 Charging load curves for node 10 in a typical week and a high temperature week 4)拥堵状况严重情况下电动汽车充电负荷 将节点15典型周与拥堵周工作日一天负荷进行横向比较,如图5(a)所示。仿真结果表明,当城市内交通拥堵状况恶化后,一方面会导致节点充电负荷高峰持续时间的增加,较典型周平均每天增加约3 h,另一方面会导致负荷峰值增高,较典型周增高约1 500 kW。 5)与其他方法预测结果的对比 将电动汽车数量设置为23万辆,仿真时间为 600 周,其他仿真参数以文献[20]仿真分析情形5进行设置。将各个节点充电负荷相叠加得到全区域总充电负荷,选取其中一典型日负荷数据,与文献[20]仿真结果进行对比,如图5(b)所示。仿真结果表明,本文一天充电负荷总量与参考文献方法计算结果接近,不同之处在于负荷的时间分布情况。参考文献结果在下午时段有一个充电负荷高峰,本文方法结果存在中午与下午时段两个负荷高峰,并且峰谷差相比较小。原因在于本文方法进行了实时动态的路径模拟,考虑到了路途中充电的情况,充电时间相对分散,而参考文献是将充电时间设置为电动汽车位于各个场所的时候,因而相对集中。此外,本文采用了时空转移模型,不仅可以得到负荷时间分布情况,还可以得到负荷在路途中各个地点的空间分布情况。 电动汽车充电负荷时空分布问题受很多随机因素影响,很难建立明确的数学模型。本文从城市电动汽车充电负荷出发,分析各类电动汽车移动特性与充电特性,结合马尔可夫决策理论与蒙特卡洛模拟方法,建立了各类车的时空转移模型,并计及实时交通状况与气温的影响。该方法能够充分考虑电动汽车行驶路径的随机性,方便、有效地计算出城市区域内充电负荷时空分布情况,并且能够预测交通状况与温度状况变化时充电负荷的变化,其预测结果为充电站规划、负荷调度等研究提供了依据。由仿真结果得出如下结论。 1)基于MDP的随机路径模拟能够避免最短路径算法中相同始终点电动汽车在固定地点充电的问题,体现电动汽车空间移动的随机性,更符合实际情况。 2)电动汽车充电负荷具有明显峰谷差,并且承担快充能力越强的节点峰谷差越明显,交通枢纽节点负荷波动情况最严重。 3)环境温度的升高对电动汽车能耗有着显著影响,导致节点充电负荷持续维持在高位;交通状况的恶化一方面会导致电动汽车充电负荷峰值增高,另一方面会导致峰值持续时间增长。 本文在建模仿真中做了一定的假设,一方面假设电动汽车充电设施能够充分满足电动汽车充电需求,另一方面假设温度与交通对单位里程耗电量之间没有耦合关系。因此考虑电动汽车充电排队、温度与交通的耦合是下一步的工作方向。 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。2.3 各节点充电负荷计算
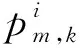
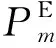
3 算例分析
3.1 交通网络
3.2 参数设置
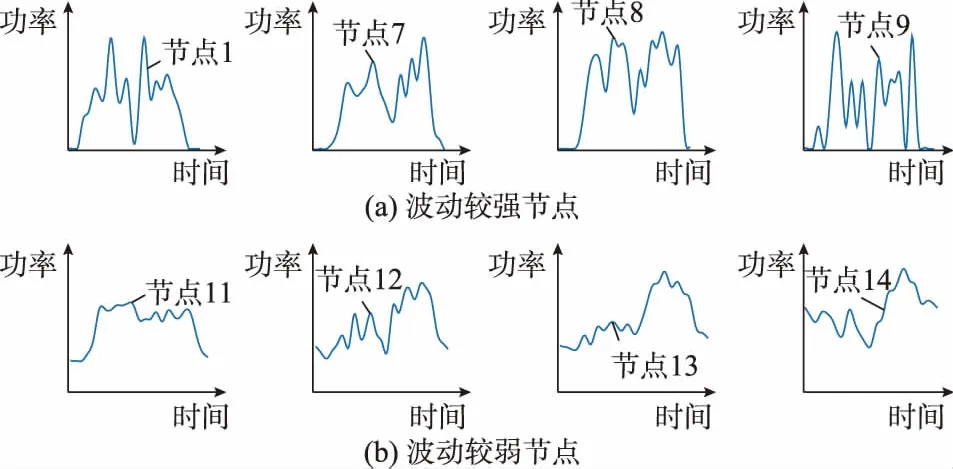
3.3 仿真结果
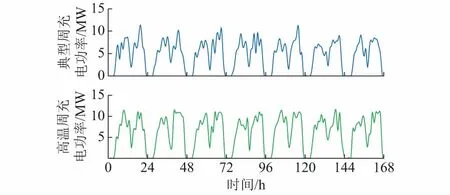
4 结语

