图尔敏论证模型在函数概念教学中的应用①

武小鹏 彭乃霞 张 怡

(黔南民族师范学院数学与统计学院 558000)

2003年4月国家教育部颁布了《普通高中数学课程标准(实验稿)》，全国陆续进入了新一轮普通高中新课程改革.本次课程改革重点强调概念学习过程要“理解基本的数学概念、数学结论的本质”，“了解概念、结论产生的背景、应用，体会其中所蕴涵的数学思想和方法”，其次还指出要提高抽象概括、推理论证等能力.[1]由此可见，数学概念的学习不应该只停留在记忆和理解概念上，掌握数学概念的论证过程，体会概念论证过程中所蕴含的数学思想方法，也是数学概念学习中不可或缺的部分.

目前的课堂教学活动，对概念的论证探究多流于形式，大多数教师都会在概念教学中按照“提出问题—组织讨论—形成概念”的模式进行程式化教学.这样的教学往往过于注重探究的形式而忽视了探究实质，造成物质性目标和功能性目标的双重缺失[2].数学是一门逻辑极其严密的学科，现有的中学数学课堂缺乏实质性的论证，即使课堂教学中形式化的讨论也不能常态化，在这种情况下，将图尔敏论证模型引入中学数学课堂，尤其是以图尔敏论证模型为依据强化数学概念的教学，可以对概念进行结构化的剖析，让学生不但掌握概念论证的过程，而且体会其中所蕴含的数学思想方法.[3]

1 图尔敏论证模型

图尔敏论证模型是英国哲学家斯蒂芬·图尔敏在20世纪50年代提出的，他在专著《论证的运用》中打破传统的数字化的论证模式，在与法学类比的基础上，提出了一个由主张、资料、根据、支援、限定词和反驳等六个功能要素构成的过程性模式，称为图尔敏论证模型(Toulmin’s Argument Pattern, TAP).[4]

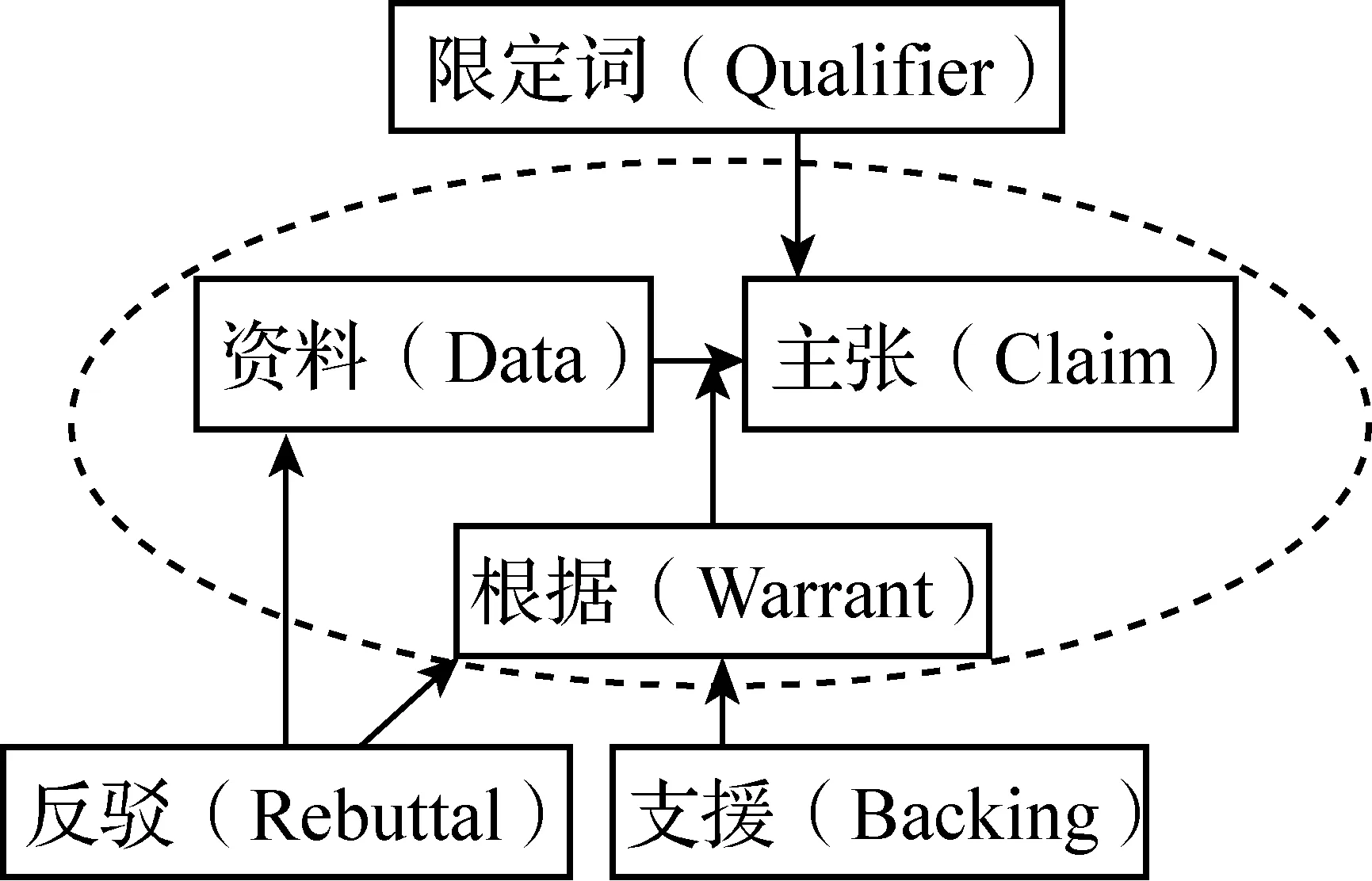
图1 图尔敏论证模型

在图尔敏论证模型中，主张、资料和根据是论证模型的核心成分，即图中虚线部分，也将其称为基本模式.基本模式连同周围的支援、限定词和反驳三个成分构成了图尔敏论证模型完整模式，也叫拓展模式.表1说明了各要素的含义.

图尔敏模型展现了一个由主张、根据、资料、支援、限定词、反驳六要素构成的论证模式，可以借此模型组织课堂教学，对数学概念进行论证，为数学概念的论证提供一个可参考的范式，学生对论证的充分性也有了明确的认识.同时，也可按照图尔敏论证模型将概念的论证通过情境转化，显化为具体实例的论证，将抽象论证问题具体化，为学生深入理解概念提供可能.Lewis和Leach 通过对中学生进行短期的知识教学干预(提供知识储备)后，证实了中学生开展论证学习的可行性；[6]类似的，Aufschnaiter等人的研究结果也认为，具体领域知识及己有知识是开展课堂论证活动的关键因素.[7]

表1 图尔敏论证模型各要素含义[5]

2 课堂论证分析

图尔敏论证模型不同论证水平是在图尔敏论证模型的基础上，结合Erduran等人的评价论证质量的分析框架划分得到的.Erduran等人从图尔敏论证模型各成分的不同组合出发，将论证分为了5个水平，具体划分见表2.

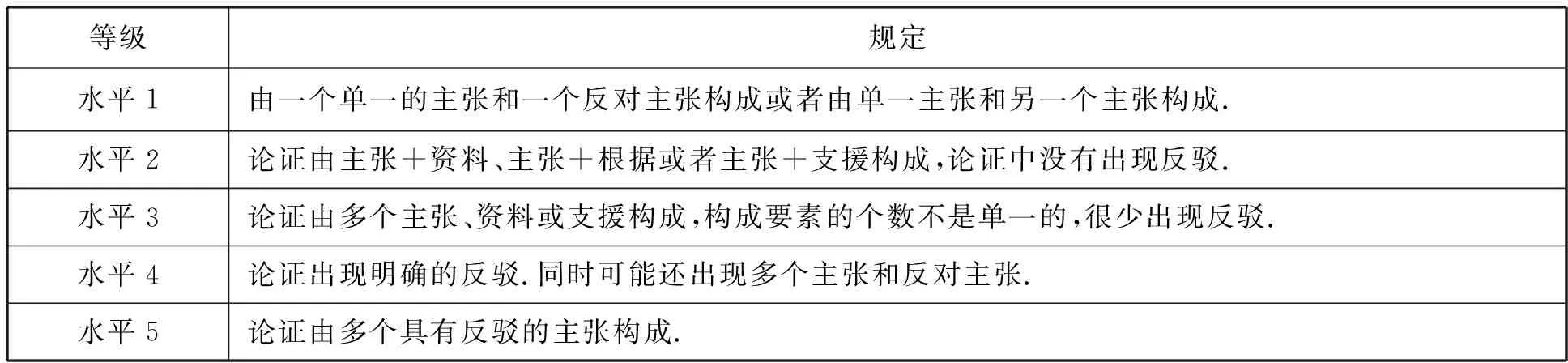
表2 Erduran评价论证质量的分析框架[8]

2.1 研究案例

本研究中，专家型教师的样本课例来自5位甘肃省首届陇原名师展示课，陇原名师是甘肃省评选出来师德高尚、素质优良、教育教学能力与教育科研能力突出的学者型、专家型中小学教学名师，这些教师在一定程度上代表了专家型教师的教学能力.新手型教师选自工作在3年之内的硕士研究生，属于入职不久的新手.为了排除额外因素的干扰，让新手型教师和专家型教师选取同样课题，即“同课异构”的形式.为了研究方便将专家型教师(Expert Teacher)简记为ET,新手型教师(Novice Teacher)简记为NT.[9]

2.2 图尔敏论证模型函数概念教学案例

按照图尔敏论证模型的论证规则，结合函数概念教学，笔者给出了自己的理解.针对函数概念的某些知识点，按论证要素多少的原则，分成不同的论证水平.

案例主题：函数概念的理解[10]

背景：学生在高中阶段刚接触到函数概念的集合定义方式，多数学生在理解上都存在困难，或者理解不够深刻等.

论证水平1：

主张：函数是由集合A到集合B的一种对应关系.

论证水平2:

主张：函数是由集合A到集合B的一种对应关系.

资料：函数f(x)=x2就是集合(-∞,+∞)到集合[0，+∞)的一种对应关系.

论证水平3:

主张：函数是由集合A到集合B的一种对应关系.

资料：函数f(x)=x2就是集合(-∞,+∞)到集合[0，+∞)的一种对应关系.

根据：函数定义表明，设A，B为两个非空数集，如果按照某种确定的对应关系f,使对于集合A中的任意一个元素x在集合B中都有唯一确定的元素f(x)和它对应，那么就称f:A→B为集合A到集合B的一个函数.

论证水平4:

主张：函数是由集合A到集合B的一种对应关系.

资料：函数f(x)=x2就是集合(-∞,+∞)到集合[0，+∞)的一种对应关系.

根据：函数定义表明，设A，B为两个非空数集，如果按照某种确定的对应关系f,使对于集合A中的任意一个元素x在集合B中都有唯一确定的元素f(x)和它对应，那么就称f:A→B为集合A到集合B的一个函数.

支援：函数是由自变量引起因变量变化的一种对应关系.

论证水平5:

主张：函数是由集合A到集合B的一种对应关系.

资料：函数f(x)=x2就是集合(-∞,+∞)到集合[0，+∞)的一种对应关系.

根据：函数定义表明，设A，B为两个非空数集，如果按照某种确定的对应关系f,使对于集合A中的任意一个元素x在集合B中都有唯一确定的元素f(x)和它对应，那么就称f:A→B为集合A到集合B的一个函数.

支援：函数是由自变量引起的因变量变化的一种对应关系.

反驳：所有的对应关系都是函数吗？

限定词：并非所有的由集合A到集合B的对应关系都是函数，比如对应方式是“一对多”时，就不能构成函数.

2.3 论证要素比较分析

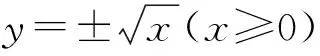
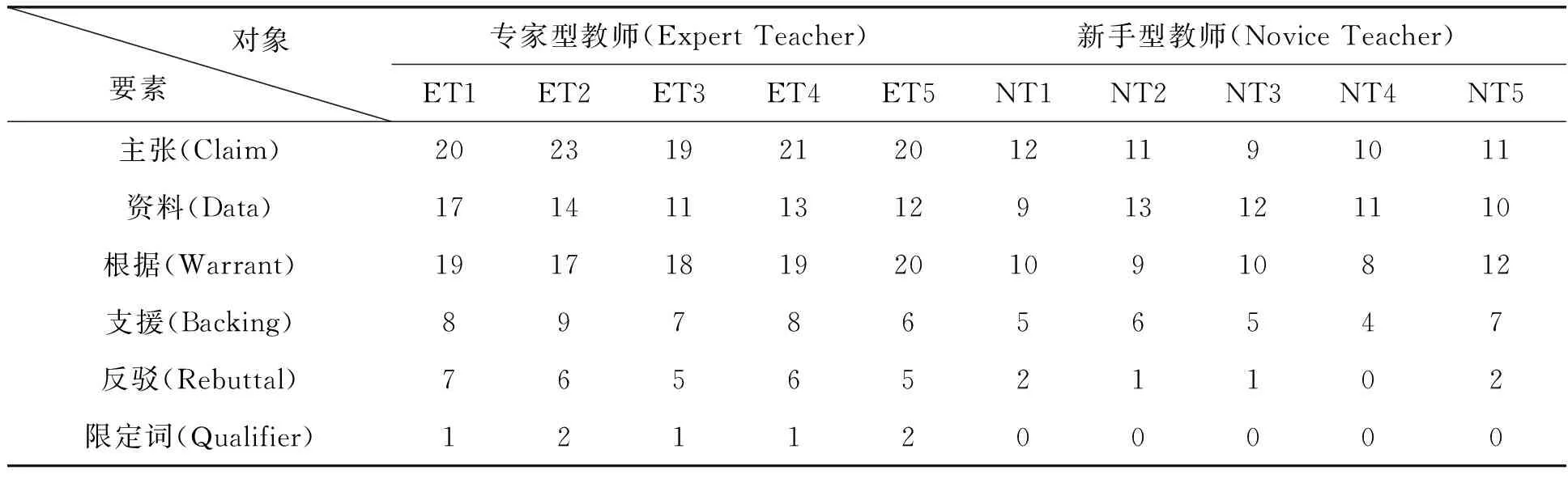
表3 课堂论证要素频数统计

根据表3，从整体上看，两类教师在高中函数概念教学中都有论证，在图尔敏论证模型各要素的统计来看，专家型教师各要素的统计频数要明显高于新手型教师.综合各要素可以说明专家型教师在数学函数概念教学中，能够提供更多的观点和主张供学生参考，提高学生对函数概念教学的认识，在多元化观点的基础上又提供了更多的支持材料，使得含有概念的教学的论证更加有理有据，同时，在反驳和支援这两个体现高水平论证的要素来看，专家型教师在概念教学的论证方面给学生提供了更多反驳的机会，让学生消除函数概念中更多的疑虑.专家型教师应用了结构较复杂的论证，论证水平相对较高.但是在限定词的使用上，两类教师都比较少的使用了限定词，新手型教师甚至没有使用限定词.限定词是用来说明主张能够让人信服的说服力程度的词，这说明两类教师都选择了说服力较好的资料.但是新手型教师直接没有使用限定词，这在一定程度上说明新手型教师的论证过于绝对，很有可能对特殊情况考虑不周.

2.4 论证水平比较分析

按照Erduran评价论证质量的分析框架表2的分析，对函数概念教学的内容进行论证水平统计，为了得到明显有效的对比，笔者给统计水平赋予了分值，赋值方法是：水平等级乘以该水平上的统计总频数，例如专家型教师水平2的统计频数分布为6,5,7，因此其总分就为(6+5+7)×2=36分，得到统计表4.

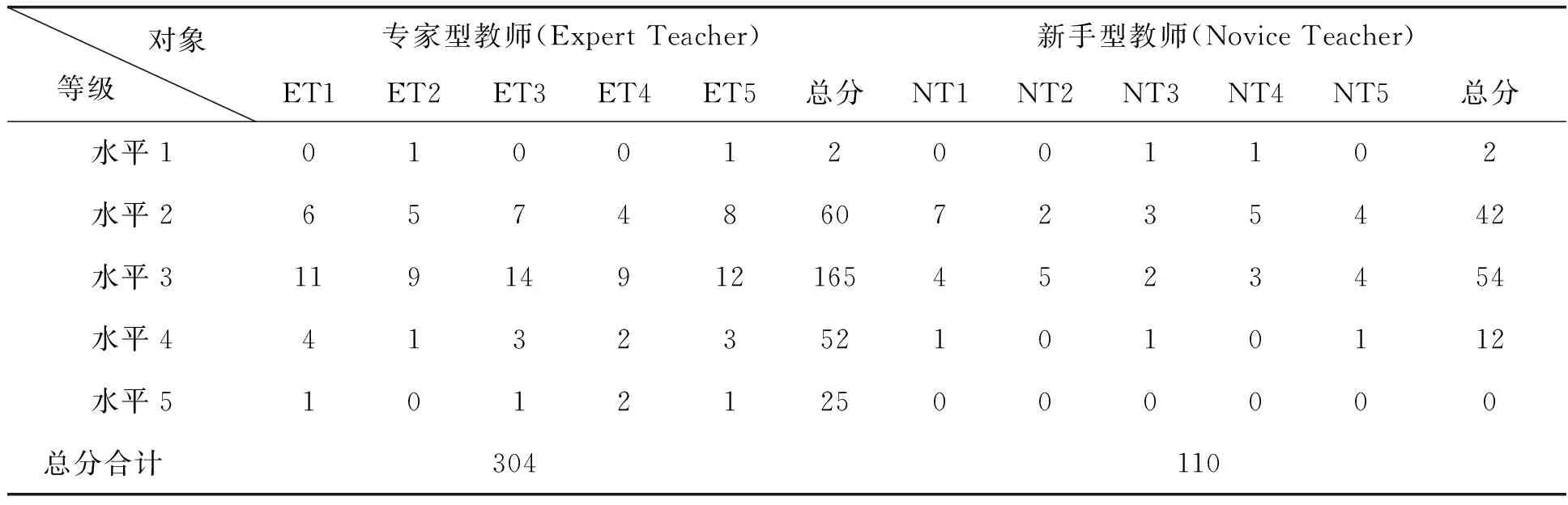
表4 课堂论证水平统计

根据表4的统计可以看出，专家型教师各个水平的论证次数都要比新手型教师多，从总分上看，水平1的得分两者相同，水平2上专家型教师和新手型教师分别为60和42分，比例为3:2，差距不是很大，说明两类教师在低水平的论证上表现基本一致.在水平3上可以看出，专家型教师的论证水平得分是新手型教师的3倍多，水平4上更是达到了4倍多，水平5新手型教师没有出现，这些数据表明专家型教师和新手型教师在高水平论证上表现出明显的差异.

3 结论与启示

通过对图尔敏论证模型的分析，结合以上研究结果，将以得出以下研究结论和启示.

3.1 观点主张是数学概念教学的主体

观点的丰富性体现了对概念理解的广度和深度，全方位、多角度分析是教师引导学生思考问题的方式.论证是否充分，学生对概念论证的感受是否深刻也体现在观点的丰富性上.课堂教学，尤其是概念性的课堂教学中，教师能够提出多元化的观点或者给学生提供不同的探究视角，这样可以为概念的建构支撑起清晰的框架.观点可以是教师直接给出，也可以用问题的形式提出，让学生在回答该问题的过程中形成对概念的整体架构.通过以上研究可以发现专家型教师提出的主张明显多于新手型，因此，新手型教师在教学中增加观点和主张是十分有必要的.

3.2 论证素材是数学概念教学的血肉

在进行概念论证过程中，提出观点和问题只是论证的一个方面，针对不同的观点能给出合理科学的解释也是至关重要的.在概念教学中，教师要引导学生将论证的焦点集中在论证素材的搜集、整理、加工上.因此，要使概念理解更加透彻，只增加观点和主张显然是不够的，如果给出的观点没有得到很好的材料和根据支援，那么仅仅是观点的堆砌，就不能让学生深入地理解概念，反而增加了学生的负担.在观点给出后一定要充分地加以解析说明，最好利用事实材料或者已有原理加以说明，这样可以增强学生的迁移意识，让学生在大的背景下理解概念，内化概念.丰富的素材让概念教学的论证更加饱满，学生在对论证素材搜集、整理、加工的过程，也充分体现了概念的形成过程，课堂教学中过程与方法目标得到了有效地落实.

3.3 反驳质疑是数学概念教学的灵魂

培养学生的创新意识，是课堂教学承载的一项重要任务，然而反思质疑正是培养创新思维的抓手. 学生通过对论证过程中诸环节的反思质疑，进一步对论证过程升华，从论证中培养学生善于思考，乐于发现的品质. Osborne等人认为,反驳的出现更能提升论证的品质, 提高论证空间质量.[11]概念教学一般都涉及到本原性问题，学生在学习概念时往往存在较多的疑惑，教学中抓住这一特点可以激活课堂，培养学生的创新意识. 同时，要深入的理解概念，反驳和质疑成为了课堂中不可或缺的要素. 本研究中主要分析了教师对概念提出的质疑，其实在现实课堂中，更多的反驳和质疑是学生提出的. 学生通过和教师的对话，消除自己对概念理解上的疑虑.由于不同的学生对概念的理解不同，产生的疑虑也不同. 教师通过解除不同学生的疑虑过程，能够更全面地了解学生，做到课堂教学面向全体学生.

3.4 高水平论证是数学概念教学的追求

Aufschnaiter等人认为, 从建构主义视角来看, 进行论证必然有助于学科知识的建构, 提高学生概念理解水平.[12]图尔敏论证模型中，根据论证的要素以及要素间关系对论证水平进行了划分，高水平的论证可以较好促进学生抽象概括能力和推理论证能力的培养.因此，数学概念课的教学，教师要引导学生向高水平的论证发展，充分的展现论证的丰富性和多元化，促进学生复杂思维的训练.在教师论证水平的统计中可以得到，高水平的论证是教师教学素质的直接体现.增加论证的复杂性和全面性，有助于学生更加深刻地理解概念和运用概念解决实际问题.高水平的教学可以更进一步增强学生的探索意识、强化学生的创新精神、提升学生的创造力.研究表明，提高学生的科学论证能力必须通过具体的论证教学，让学生有机会参与论证活动.明确的论证教学(学生参与具体的论证活动与有明确论证教学目标的教学)能促进学生对科学概念的理解、有益于学生论证能力的提高.[13]

注重课堂的论证过程是课堂教学发展的必然趋势，是提高学生科学素养，培养适应现代社会及未来需要的全面发展的人才的必然要求.目前国内对论证教学法的研究还比较少，已有的研究大多是对国外研究现状综述.而基于图尔敏论证模型课堂教学研究更少，仅有的研究也只是对该模型的简单介绍.国内的论证式教学研究并没有实证性的教学研究成果.因此，利用图尔敏论证模型进行指导课堂论证教学在国内具有广阔的研究前景.[14]如能将图尔敏模型的论证过程和具体现实情境相整合，让抽象的论证过程直观化、生活化，将对学生理解抽象的论证过程起到辅助作用.同时，图尔敏论证模型也同样是问题论证的一种思路，一个视角，这种逻辑学的论证观点可以将抽象的论证过程和现实生活拉得更近，有助于培养学生严谨、求真、善思、明辨的可贵品质.