三浮陀螺磁悬浮干扰力矩误差建模*
王 雪,杨志超,邓忠武, 马 宁
(1.北京航天控制仪器研究所,北京 100854;2.陕西航天时代导航设备有限公司,陕西 宝鸡 721000)
三浮陀螺是精度等级较高的惯性仪表,其性能在很大程度上决定了惯性平台系统所能达到的最高指标[1-3]。误差模型是研究误差规律的数学模型,建立误差模型是进行误差分析和提高陀螺使用精度最常用的手段[4-7]。
对陀螺设计师而言,提高陀螺精度是设计的主要任务之一,因而,应熟知每项误差的产生原因和变化规律,以便在设计和生产中采取措施。根据不同需要,可以对陀螺建立各种类型的误差模型[8-11]。对于航天运载器而言,大的加速度是其显著特点,因此特别注重误差和加速度之间的关系,三浮陀螺的建模也是基于这个原则进行研究的。
1 径向磁悬浮的影响分析
在三浮陀螺中,磁悬浮支承的应用可以起到消除残余重浮力差、并使浮子精确定中的作用;但由于加工和装配中种种不理想因素的存在,使得磁悬浮在完成以上功能的同时,给陀螺引进了新的干扰力矩源——磁悬浮干扰力矩[12-13]。为了对磁悬浮干扰力矩进行测试和补偿,首先要对其进行建模。根据干扰力矩与运动物体加速度之间的关系,可以把干扰力矩分成三大类:绕输出轴与比力无关的干扰力矩M0;绕输出轴与比力一次方成比例的干扰力矩M1;绕输出轴与比力二次方成比例的干扰力矩M2。绕输出轴总的干扰力矩MF可以写成:
MF=M0+M1+M2+Mξ
(1)
将式1除以转子的角动量,并整理成单自由度液浮积分陀螺常用的静态漂移误差模型:

(2)
式中,ωF为陀螺仪相对于惯性空间的总漂移率;aI为沿输入轴IA方向的比力分量;aS为沿自转轴SA方向的比力分量;aO为沿输出轴OA方向的比力分量;DF为与加速度无关的常值漂移率;DI为与沿IA方向的比力成正比的一次项漂移系数;DS为与沿SA方向的比力成正比的一次项漂移系数;ξ为陀螺仪随机误差,由模型中未考虑的因素所造成的漂移率。
下面,将对照三浮陀螺误差的建模过程建立磁悬浮的误差模型。
通常,对该模型中的各误差项系数进行讨论时认为,磁悬浮干扰力矩所产生的陀螺漂移与过载无关,可以归算到零次项漂移中。然而,通过对干扰力矩的产生机理进行深入的分析可知,磁悬浮系统干扰力矩除了可以产生零次项漂移外,还会产生一次项漂移和随机漂移。下面分别研究不同原因引起的磁悬浮干扰力矩与陀螺误差模型之间的关系,并对磁悬浮干扰力矩进行建模。
磁悬浮系统工作的目的之一是使陀螺浮子组件承受外力之和为零,因而有:
FCXF=(m-ρV)a
(3)
式中,FCXF为磁悬浮系统施加给浮子组件的作用力;m为浮子组件的质量;ρ为浮液的密度;V为浮子组件的体积;a为浮子组件相对惯性空间的加速度。
将式3沿陀螺IA、SA轴分解得:
FIA=(m-ρV)aS
(4)
FSA=(m-ρV)aI
(5)
径向磁悬浮包括偏心误差干扰力矩MjA和圆度误差干扰力矩Mjo。
将径向磁悬浮转子相对浮子轴的偏心δ分解成沿陀螺的自转轴SA的分量δIA和沿输入轴IA的分量δSA,得到由于偏心将δ产生的绕输出轴的干扰力矩:
MjA=(m-ρV)δSAaS+(m-ρV)δIAaI
(6)
由于转子圆度误差产生的绕输出轴的干扰力矩:
MjO=2(m-ρV)δOaS+2(m-ρV)δOaI
(7)
式中,δO为径向转子圆度。
则总的径向磁悬浮干扰力矩为:
MJ=MJA+MJO=(m-ρV)(2δO+δSA)aS+
(m-ρV)(2δO+δIA)aI
(8)
式8将径向磁悬浮干扰力矩与陀螺漂移模型联系了起来。它的用途在于:一方面,可以将径向磁悬浮干扰力矩的常值分量作为陀螺比力一次项误差来进行补偿,以提高陀螺的使用精度;另一方面,通过合适的试验方法,可以将磁悬浮干扰力矩从陀螺漂移中分离出来,并得到磁悬浮元件的相关参数,为系统的优化设计提供基础和依据。
2 定中位置的影响分析
在分析定中位置的影响时,可以将磁拉力分成与过载无关和与过载相关两部分分别进行研究。
浮子不同定中位置示意图如图1所示。图1中,O点为磁悬浮信号中心,O′点为软导线的力中心,启动过程结束后磁悬浮会将轴尖由O′点拉到O点,f为轴尖处于O′点和O点时6根软导线合力的差值。

图1 浮子不同定中位置示意图
该力在x和y方向的分力就是磁拉力在O点和O′点沿径向方向加力的增量,同理可以得到该力在轴向方向加力的增量,即:
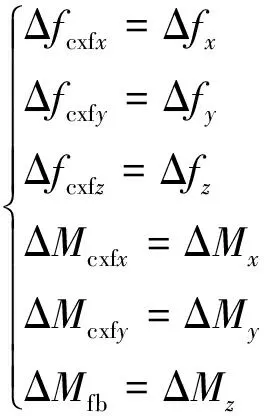
(9)
式中,Δfcxfx、Δfcxfy、Δfcxfz分别为磁拉力的增量在各轴的分量;Δfx、Δfy、Δfz分别为软导线的合力差值沿各轴分量的增量;ΔMcxfx、ΔMcxfy分别为磁拉力矩的增量在x、y轴的分量;ΔMfb为力反馈回路反力矩的增量;ΔMx、ΔMy、ΔMz分别为软导线合力矩的差值沿各轴分量的增量。
不同磁悬浮定中位置造成的磁悬浮干扰力矩的差值ΔM为:
ΔM=ΔfcxfxΔlx+ΔfcxfyΔly+ΔfcxfzΔlz+ΔMfb
(10)
式中,Δlx、Δly、Δlz分别为不同定中位置造成的磁拉力作用点相对于浮子轴的等效距离。式10的值只受定中位置的影响,并随着定中位置的变化而变化,与过载无关。
磁拉力除了需要平衡软导线的分力外,还需要克服残余重浮力差,使浮子组件上的合外力和合外力矩均为零。重力与浮力均与比力成正比,为满足上述条件,磁悬浮加力也应该与比力成正比;因此,磁悬浮用来克服残余重浮力差的那部分磁拉力所产生的附加干扰力矩也应该与比力成正比。
由以上分析可知,磁悬浮定中位置对仪表精度的影响一部分可以通过软导线间接地反映出来,表现在零次项漂移系数的变化上,不同的定中位置对应着不同的零次项。在实际工作条件下,受磁悬浮定中精度的影响,O点的位置存在随机分量,因此,此项干扰力矩中也包含了一部分随机分量。
3 误差模型的建立
影响磁悬浮干扰力矩的要素如图2所示,将这些影响要素按照与力臂相关和与力相关进行分类,以便于建立总的磁悬浮干扰力矩模型。磁悬浮干扰力矩等于磁拉力与等效力臂的乘积。与力臂相关的量由磁悬浮元件的结构参数确定,它的大小与磁性材料的稳定性、框架组件尺寸的稳定性、元件的机加和装配的工艺要求、仪表的调试要求等和结构相关的因素有关,与过载无关;因此,磁悬浮干扰力矩所对应的漂移的类型由力的类型决定。
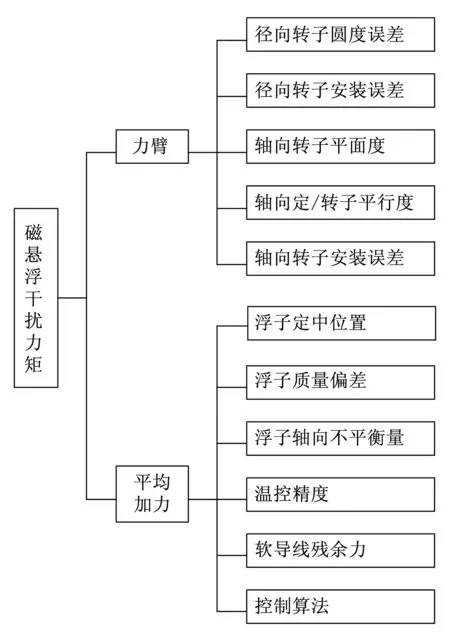
图2 磁悬浮干扰力矩的影响要素
图2中,与磁悬浮平均加力相关的各项与过载的关系如下。
1)磁悬浮定中位置决定了软导线的残余力的大小和沿着磁悬浮支承轴线的各个方向上分力的分布,克服此力的磁拉力与过载无关。
2)温控精度包含两部分的含义,即温度点的准确度和温度点的精密度(即波动量)。其中,温度点的准确度决定了浮力的大小,它与浮子的质量偏差共同确定了剩余的重浮力差值,克服此力的磁拉力与过载成比例。
3)浮子的轴向不平衡量产生轴向不平衡力矩,其大小由浮子的质量分布和浮力分布确定,克服此力矩的磁拉力与过载成比例。
4)叠加在温度点和磁悬浮定中位置稳态值上微小的波动量、电气噪声和控制算法等的影响,造成了磁拉力中包含一部分的随机分量。
与陀螺静态误差漂移中的各个项相对应,与过载无关的磁拉力与力臂相乘产生零次项漂移,与过载成比例关系的磁拉力和力臂相乘产生一次项漂移,磁拉力和力臂的随机部分相乘产生随机漂移。除此之外,在位置信号采样周期,转子分度误差造成的磁悬浮元件的不对称性会产生磁滞干扰力矩,该力矩与过载无关。
如果不考虑随机项,磁悬浮干扰力矩只影响陀螺确定性漂移中的零次项和一次项漂移系数,因此,可以参照陀螺漂移模型,将磁悬浮干扰力矩写成与比力相关和与比力无关两部分:
MC=MC0+MC1
(11)
式中,MC为总的磁悬浮干扰力矩;MC0为与比力无关的磁悬浮干扰力矩;MC1为与比力成比例的磁悬浮干扰力矩。
磁悬浮干扰力矩造成的陀螺的零次项漂移只受到材料的磁滞效应和磁悬浮定中位置的影响,当磁性元件的材料确定并将其装表后,磁滞干扰力矩就为确定量,仪表湿对中后,定中位置对软导线的影响也为确定量;因此,对影响零次项的MC0的测试和分析都很简单,本文着重讨论影响一次项的MC1。
考虑浮子轴向不平衡、重浮力差和磁悬浮元件的加工、装配误差可以得到MC1:
(12)
式中,ml、mr为左、右半个浮子的质量;ρl、ρr为左、右半个浮子的平均密度;Vl、Vr为左、右半个浮子的体积;δOl、δOr为由于左、右两侧径向磁悬浮转子的圆度引起的力臂分量;δIAl、δIAr为左、右两侧径向磁悬浮转子相对浮子轴偏心δ沿陀螺自转轴的分量;δSAl、δSAr为左、右两侧径向磁悬浮转子相对浮子轴偏心δ沿陀螺输入轴的分量。令:

(13)
式中,δSl、δIl、δSr、δIr这4项综合地表征了由于结构上的不理想所造成的磁悬浮干扰力矩等效力臂的大小,它反应了磁悬浮元件总的加工水平和能力。
将式13代入式12,可得:
(14)
浮液的密度ρ和浮子组件的体积V都是温度的函数,因此,在进行磁悬浮干扰力矩的建模时应考虑温度的影响。令:
(15)
式中,ρ0为初始温度时浮液的密度;V0为初始温度时浮子的体积;α为浮液密度的温度系数;β为浮子组件体积的温度系数;ΔT为实际温度与初始温度的差值。
将式15代入式14,整理得到磁悬浮干扰力矩的解析表达式为:
(16)
设初始温度为T0时,磁悬浮干扰力矩为MC10,则:
(17)
当温度变化了ΔT时,磁悬浮干扰力矩为MC1,则磁悬浮干扰力矩随温度变化的增量表达式为:

(18)
结合式16和式18,可以得到如下2点结论。
1)δSl、δIl、δSr、δIr与仪表的装调过程有关,一旦三浮陀螺完成整表的装配和调试,磁悬浮干扰力矩MC1和干扰力矩增量ΔMC1只是过载和温度的函数。
2)对于同一只陀螺来说,当温度恒定时,MC1与过载成比例;当过载恒定时,ΔMC1与[(α-β)ΔT+αβΔT2]成比例,由于β≪α,忽略二阶小量时,ΔMC1近似与ΔT成比例。
根据以上推导得到的磁悬浮系统干扰力矩MC1与过载和温度之间的关系,可以设计相应的试验方案,对磁悬浮的干扰力矩进行测试。
4 模型的验证
根据测量公式中的待测量可制定试验方案。试验步骤的设计总体上与陀螺六位置分离误差系数的试验相同,不同的是,在每一个位置正常进行测量后要断掉磁悬浮系统的加力电流,并在很短的时间内对此位置的力反馈电流进行测量,根据2次的测量结果得到三浮陀螺磁悬浮系统的干扰力矩。
考虑到磁悬浮和温度之间的关系,还需要通过变温对不同温度下磁悬浮干扰力矩进行测量。测试结果见表1。

表1 不同温度下磁悬浮干扰力矩对应漂移系数
根据以上测试结果,可以看到磁悬浮干扰力矩在陀螺零次项中的分量与温度无关。磁悬浮干扰力矩在陀螺一次项中的分量与温度成比例,并且温度变化时,一次项的变化量与温度差成比例。该测试结果与建模得到的结论相符。
磁悬浮干扰力矩造成的陀螺的一次项漂移与温度相关,其数值随温度成比例变化。其根本原因是由于磁悬浮干扰力矩的产生是伴随着磁悬浮元件加力而产生的,而磁悬浮加力是由相应温度的重浮力差决定的,重浮力差随着温度的变化而变化,造成了磁悬浮干扰力矩也受仪表温度的影响。三浮陀螺磁悬浮干扰力矩的测试结果证明了理论建模的正确性,验证了试验方案的可行性。
5 结语
对照陀螺的漂移模型建立了磁悬浮干扰力矩的模型,考虑到磁悬浮干扰力矩对原有陀螺误差模型中各项的影响,建立了新的三浮陀螺漂移误差模型,对磁悬浮干扰力矩实现了“软”补偿。磁悬浮干扰力矩会产生陀螺零次项和一次项漂移,通过设计试验,可以将磁悬浮干扰力矩从陀螺漂移模型中分离。根据磁悬浮干扰力矩和磁悬浮平均加力可以估算出干扰力矩等效的力臂,该值可用于仪表的机加装配过程检查和仪表的设计改进。

