三线摆微推力测量系统的阻尼控制优化法
郑慧奇,徐焱林,丁 亮,顾 磊
(北京卫星环境工程研究所,北京 100094)
0 引言
针对微推力测量,国内外已经开展大量的研究,形成若干成熟的测量方法。例如:日本Murakami等人[1]使用气浮装置实现无摩擦转台测力结构,用无摩擦的方式支撑平台,通过测量微推力产生的转矩或平衡转矩的平衡力来达到测量的目的;美国NASA Lewis研究中心及普林斯顿大学都设计了倒立摆结构的推力架,用于大功率电推进器的推力测量[2-3],其测量原理是推进器工作时倒立摆以底部为轴发生偏转,通过测量摆的位移获得推力值;平行四边形的测力结构中,安装推进器的顶板与固定底板可相对平行地移动,但是上、下板间的移动受到弹簧约束,通过力矩平衡来确定推力大小[4];天平结构的测量原理是将推进器及其附件的重量预先平衡,再由测量元件产生相应的平衡力来平衡推进器产生的微推力[5];北京航空航天大学研制了全弹性微小推力测量实验台架,采用力矩平衡原理进行测量,通过双叉形弹簧片消除支撑结构的摩擦影响[6];哈尔滨工业大学利用三线摆结构,采用扭矩平衡和光杠杆放大原理实现电推进器微小推力的测量[7]。
三线摆理论成熟,工程上已经被广泛应用在刚体转动惯量测量领域[8-10],另外也被用来测量重力加速度[11]。由于其具有结构简单、操作方便的优点,近年来哈尔滨工业大学宁中喜等人将三线摆应用于微推力测量中[7]。利用三线摆测量微推力时,推力平台产生的角位移与微推力大小一一对应,测得这一角位移便可以根据标定结果反推确定微推力大小。由于推力平台与固定结构通过3根金属丝线悬吊连接,全部结构中不存在宏观的摩擦副,推力平台几乎只受到微推力、重力和丝线拉力的作用,因而转动灵活,对推力变化敏感,转动范围内无死区,使得三线摆测量具有灵敏度高、精度高、重复性好的优点。
本文介绍三线摆微推力测量的原理,分析测量结构的阻尼特性及其影响,提出阻尼控制方法以优化测量系统。
1 三线摆微推力测量原理
如图1所示,三线摆微推力测量系统的核心部件为3根金属丝线(摆线)及推力平台组成的悬吊结构。3根丝线悬挂点确定了推力平台的旋转轴线,在轴线一侧放置被测推力器或推力收集板,另一侧为用于保持推力平台处于水平状态的配重,微推力作用方向与由推力平台中线及转轴确定的平面垂直;施加推力后,推力平台围绕旋转轴线转动。

图1 三线摆微推力测量系统Fig. 1 Trilinear pendulum micro-thrust measurement structure
三线摆的摆盘(即推力平台)呈长条状,在推力作用下发生转动,可通过光学测量手段确定其转动角度θ,并根据标定结果反推出对应推力的大小。这就是三线摆法测量微推力的基本原理。
测量中忽略影响角位移的其他干扰因素,则微推力作用下,达到稳态时推力平台发生的角位移为

式中:F为微推力;L为微推力对转动轴线的力臂,本文研究的三线摆L=0.35 m;R为推力平台的转动刚度。
由式(1)可见,一定推力作用下,整个系统输出的角位移大小决定于推力平台的转动刚度:刚度越小,产生的角位移越大。
丝线悬挂的推力平台的运动几何关系如图2所示,一定角位移下的回复力矩主要来自金属丝线拉力产生的沿转动方向的力矩,力矩的大小由角位移决定。
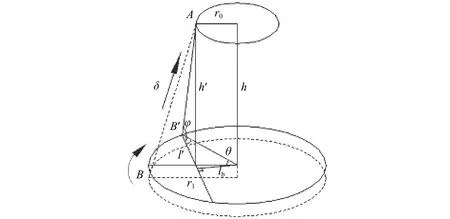
图2 推力平台的运动几何关系Fig. 2 Geometric relations in the motion of the thrust stand
设摆线上端与转轴间的距离为r0,摆线的下端与转轴间的距离为r1,在摆动过程中当推力平台的角位移从0变为θ时,摆线从AB位置旋转至AB′位置,相应的推力平台与上端固定点间的距离从h变为h′,此时摆线AB′在摆动平面上的投影为l′,设此时摆线与推力平台的夹角为

单根摆线上的拉力T将随着推力平台转角的改变而发生变化,由其分量产生的回复力矩也不断变化。当推力平台转角为θ时产生的回复力为

式中:Fb为摆线拉力在推力平台平面上的分量;G为推力平台的总重量。
3根摆线能够产生的回复力矩为

当推力平台在恒定推力作用下达到稳态时,摆线产生的回复力矩与推力力矩达到平衡,即

设摆线长度为δ,则

推力平台与上端固定点在竖直方向的距离

本文所研究的三线摆结构:r0=0.04 m,r1=0.05 m,h=0.45 m,则计算得到推力平台在不同摆动角度下的h′及高度变化 Δh=h−h′,如表1所示。

表1 推力平台在不同摆角下的h′及ΔhTable 1 Parameters h′ and Δh at different angles of oscillation
由表1可见,在推力平台的角位移达到45°时,高度变化量Δh<1.5 mm。由于测量系统使用环境及工况均不允许其摆角过大,20°以下的摆角范围已能完全覆盖使用工况。θ=20°时推力平台的高度变化Δh<0.27 mm,此时以h代替h'造成的误差将小于0.06%,以θ代替sinθ带来的误差亦小于2.1%,因此可将式(5)简化为

则三线摆测量系统推力平台的转动刚度为

本文所研究的三线摆测量系统推力平台及其上所有结构的质量约为10 kg,由式(8)可得,其在50 mN推力作用下达到稳态时的角位移约为2.3°。
2 摩擦阻尼条件对测量的影响
对设计制作良好的三线摆微推力测量系统,运动部件不存在明显的摩擦副,其受到的摩擦阻尼作用十分微弱,假设施加微推力F(t)作用,摆动的微分方程为

式中:I为推力平台的转动惯量;ζ0为推力平台的阻尼系数。
测量系统输出角位移θ相对被测推力F的传递函数为

推力平台的转动惯量I=1.4 kg·m2,由实测ζ0=0.03,可以求得式(11)中的阻尼比ζ=0.019 2,可见系统为典型的欠阻尼系统,仿真分析得到其在F=50 mN恒定推力作用下(设推力从t=10 s开始施加)的推力平台角位移如图3所示。

图3 弱阻尼时恒定推力作用下的推力平台角位移Fig. 3 Angular displacement of weak damping system under constant thrust
由图3可见,推力平台在恒定推力作用下将围绕稳态的平衡位置往复摆动,且摆动幅值衰减缓慢:在施加推力作用近300 s时,推力平台仍然有约0.2°的摆动幅度。而考虑到实际测量条件,若此时读数将产生约4 mN的偏差。可见,欠阻尼的三线摆微推力测量系统进入稳态的时间过长,测量效率低下。
假设推力平台在运动过程中受到恒定的滑动摩擦阻尼力Ff作用,力臂为L,在其作用下的推力平台受力如图4所示,其方向始终与平台的运动方向相反。

图4 阻尼力Ff作用下推力平台的受力Fig. 4 Force condition of the thrust stand platform


代入三线摆参数,仿真分析得到在恒定阻尼力作用下的推力平台角位移,如图5所示。

图5 恒定阻尼力作用下的推力平台角位移Fig. 5 Angular displacement under constant friction
由图5可见,推力平台摆动中若存在大小恒定的滑动摩擦阻力Ff,将使推力平台的稳态角位移产生偏差。原因是,摩擦阻尼力作用下,推力平台在往复摆动的低速区间段将存在死区,处于死区的推力平台受力情况为

其中Ffs为推力平台受到的静摩擦力。由式(14)可见,摩擦阻尼力的持续存在使推力大小与角位移不再具有式(5)所描述的确定的对应关系。从仿真结果还可以看出,具有滑动摩擦阻尼力作用时,推力平台振幅衰减迅速,进入稳态的速度明显加快;并且摩擦阻尼力越大,进入稳态的速度越快,但稳态角位移的偏差也越大。
3 外加阻尼力优化
根据第2章的分析可见,增加推力平台的恒值滑动摩擦阻尼力能有效缩短系统进入稳态的时间,但会导致测量结果的偏差,因此考虑在推力平台的摆动过程中施加脉动摩擦阻尼,对三线摆微推力测量系统进行优化。本文设计的阻尼控制机构由摩擦块、摩擦驱动器及控制器组成,如图6所示。

图6 阻尼控制机构示意图Fig. 6 Schematic diagram of the damping control mechanism
滑动摩擦阻尼来自摩擦块与推力平台之间的相对滑动。摩擦块只能通过弹簧,在驱动器的推动下做垂直于平台面的微幅移动。阻尼控制通过摩擦驱动器完成,驱动器的执行构件进行直线移动,通过其位移准确地控制弹簧的压缩量,从而控制摩擦块对推力平台的压力,保证推力平台在摆动状态下受到相应大小的摩擦阻力作用。
测量开始后,摩擦块对推力平台施加垂直于接触平面的脉动压力,且压力值按图7所示规律逐步减小,直至80 s时压力作用彻底消失。每个压力作用周期分为3个阶段,第1阶段压力线性增大,第2阶段压力线性减小至0,第3阶段内压力保持为0。压力作用彻底消失后,摩擦块将返回初始位置停留并保持与推力平台无接触状态,此时推力平台的运动状态将不再受到摩擦块的干扰。

图7 摩擦块施加压力曲线Fig. 7 Pressurizing curve of the friction block
推力平台在摆动过程中,只要其速度不为0且摩擦块施加的脉动压力存在,都将获得大小正比于压力的脉动滑动摩擦阻力,只是其方向随推力平台摆动方向变化而改变。脉动摩擦阻尼的作用在于:推力平台进入稳态前,当Ff≠0时,推力平台的机械能不断耗散,使摆动幅度衰减;当Ff=0时,推力平台处于弱阻尼状态,可以跳出或避免由摩擦力造成的死区,保证稳态角位移大小不受摩擦力的影响。
4 推力平台角位移仿真及实验验证
按照图7所示的外加阻尼施加方式,对推力平台的角位移进行仿真,结果如图8所示。在50 mN恒定推力,加之脉动摩擦阻尼力作用下,推力平台的角位移输出在大约30 s后基本达到稳态,比未施加摩擦阻尼时的动态时间大大缩短;且脉动摩擦阻尼不会造成系统稳态下的角位移偏差,保证了微推力测量的精度。

图8 脉动阻尼力作用下的角位移Fig. 8 Angular displacement under pulsed friction
为直观分析脉动摩擦阻尼力作用下推力平台摆动角速度的衰减情况,我们按照前述设定工况进行仿真分析,得到摆动角速度和滑动摩擦力的对应关系如图9所示。由图可见,推力平台处于摆动状态下,滑动摩擦力与摆动方向相反并导致摆动角速度的幅值逐渐减小。推力平台摆动受到微推力矩、摆线回复力矩及摩擦力矩共同作用,在摆动速度为0且微推力矩与回复力矩的合力矩不足以抵消摩擦力矩时将进入死区,此时静摩擦力矩将阻碍推力平台继续移动;由于摩擦块对推力平台施加的压力为脉动形式且幅值不断减小,所以摩擦块提供的摩擦力矩将不能长时间维持推力平台处于死区位置,届时推力平台将继续向稳态位置摆动,而在推力平台移动中摩擦力将进一步消耗其动能,如此往复,造成推力平台角速度幅值不断衰减,同时摩擦块的作用力也逐渐减小直至消失。逐步减小并最终消失的脉动摩擦阻尼能够保证推力平台无摩擦地停留于稳定状态,且这一状态仅由微推力矩与摆线回复力矩的平衡来决定,即由式(5)描述的稳态。可见,按图7所示外加阻尼规律控制摩擦块作用于推力平台,不会对测量结果造成任何影响。

图9 滑动摩擦力与角速度关系Fig. 9 Correlation between sliding friction and angularvelocity
在实验室按照上述参数设定进行了试验,验证了仿真结果的正确性。实测在恒定微推力作用30 s时推力平台摆动停止,稳态下推力平台的停留位置与无外加摩擦阻尼下的稳态位置重合,证明外加脉动阻尼作用没有影响三线摆的测量精度。
三线摆的无阻尼摆动周期只与本身结构参数相关,因此确定的三线摆微推力测量系统具有固定的无阻尼摆动周期。设计脉动摩擦阻尼参数时,需要考虑无阻尼摆动周期(即脉动周期),其与摩擦阻尼力的大小都会影响推力平台摆动角位移的衰减速度,需要统筹考虑。由图10可见,脉动周期选择过小或过大都不合适,对确定的系统选择合适的脉动周期才能够缩短摆动平台趋稳的时间。

图10 阻尼脉动周期与角位移衰减Fig. 10 Relationship between damping pulsation period and angular displacement attenuation
由图11可见,摩擦阻尼力的大小也会影响推力平台角位移的衰减速度,适当增加阻尼力可以加快角位移的衰减,而选择过小的阻尼力可能导致推力平台摆动衰减的效果不够明显。
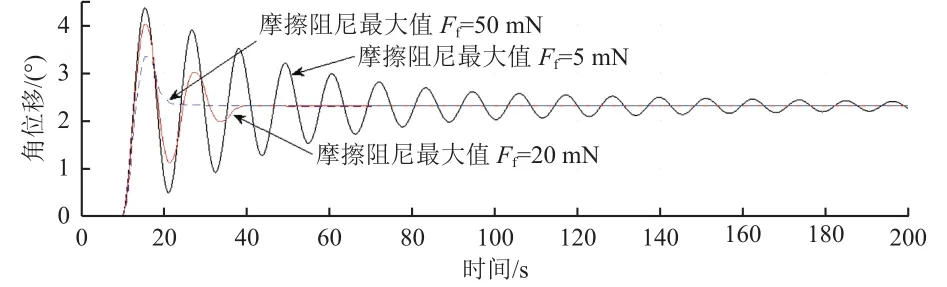
图11 脉动摩擦力大小与角位移衰减Fig. 11 Relationship between the magnitude of fluctuating friction and angular displacement attenuation
事实上,脉动周期、阻尼力大小以及摩擦块作用力的波形都会对推力平台角位移衰减产生影响,选择脉动摩擦阻尼参数时需要根据三线摆微推力测量系统的固有特性进行统筹考虑,并通过实验或仿真调整优化各个参数,才能确保正式微推力测量实验中收到较好的阻尼效果。
5 结束语
利用三线摆测量微推力时,为避免推力平台长时间处于摆动状态,对推力平台施加额外的摩擦阻尼力可以有效缩短系统进入稳态的时间。持续施加摩擦阻尼力在有效抑制平台摆动的同时会导致稳态角位移的偏差,当对推力平台施加每个脉动周期内最小值为0的摩擦阻尼时,将在消除稳态角位移偏差的同时有效衰减摆动幅度,加快推力平台进入稳态的速度。值得注意的是,脉动摩擦阻尼参数,如脉动周期、阻尼力大小、摩擦块作用力波形等都会对摆幅衰减效果产生影响,应根据具体情况对其进行设计及优化。

