水工隧洞弯道水力学特性数值模拟研究

王 丹 柏， 吴 金 旭， 刘 娅

(1.四川省紫坪铺开发有限责任公司，四川 成都 610091；2.中水北方勘测设计研究有限责任公司，天津 河西 300222；3.天津科源工程设计有限公司，天津 河西 300200)

0 引 言

水工隧洞作为水利水电工程一项基础工程，是为了输水、导流或泄洪等任务而穿山开挖建成的封闭式的输水道。其洞线布置主要考虑地形、地质条件和水力学条件等因素。实际中，为了适应地形和地质条件的限制，水工隧洞往往会设置弯道。而弯道由于自身特点，水力学特性较为复杂，是整个隧洞安全运行的关键部位，如果弯道流态不稳，流速压强分布不均，可能会造成很严重的空蚀空化问题，甚至出现掏空现象，同时弯道半径和转角的选择，还会影响隧洞的泄流能力。在以往的水工隧洞设计中，隧洞弯道的半径和转角主要是根据工程经验来确定，然后通过物理模型试验进行验证和优化，耗时且成本较高。但随着计算机性能的提高和数值计算方法的改进，数值模拟计算在水工建筑物的体型优化中得到广泛应用[1-3]，其成果也得到了大家的肯定和认可。笔者在某工程右岸导流洞数值模拟计算研究的基础上，利用Fluent软件，选择相同的控制方程、边界条件设置、算法及网格划分，进一步研究弯道半径和转弯角度对弯道内流速和压力分布的影响，为以后水工隧洞弯道的设计提供参考。

1 水工隧洞弯道设计

隧洞在设计时布置弯道是普遍存在的，而弯道设计主要考虑两个因素：一是与实际工程相关的限制条件(包括地形、地质条件等)，二是弯道水流的水力学特性。前者是客观存在无法改变的，后者可以通过选择不同的弯道半径和转角来改善。以往的实际工程大都先参照规范[4]一般规定：对于流速小于20 m/s的无压隧洞，弯道半径不宜小于5.0倍的洞径(或洞宽)，转角不宜大于60°；对于流速小于20 m/s的有压隧洞，弯道半径可以适当降低要求，但也不应小于3.0倍的洞径(或洞宽)，转角不宜大于60°；对于高流速的无压隧洞不应设置弯道；对于高流速的有压隧洞可以设置弯道，但需要通过试验确定其合理性。然后结合经验先初步拟定隧洞的半径和转角，再通过模型试验来确定其合理性。既耗时，又耗力。

表1是部分已建的水利水电工程的水工隧洞的弯道几何特性表，由该表可以看出，大部分工程的弯道转角集中在30°～60°之间，部分隧洞工程也有小于30°的转角。其中也有极个别的隧洞弯道转角大于60°，三门峡水利枢纽排沙泄洪洞的弯道转角更是达到75°。R/d大都集中在7～15之间，但弯道半径最大的有超过45倍的洞泾，最小的没有小于5倍的洞径(最小的为R/d=5.91)。由此可见，大部分水工隧洞工程都符合规范要求，说明了工程经验具有一定的可靠性。

2 水工隧洞弯道数学模型建立

在用物理模型试验验证过的导流洞三位数值模型[5]的基础上，笔者进一步以该工程导流洞为研究对象，制定9种弯道研究方案，利用Fluent软件，建立相应弯道数学模型，研究弯道水流的压力、流速分布规律及弯道转角和半径对弯道水力学的影响。数值模拟计算控制方程选择RNGk-ε模型，自由面追踪采用广泛应用的VOF方法，横向断面网格间距采用0.6 m、纵向网格间距采用0.7 m，边界条件设置、算法及其它参数设置也保持不变。

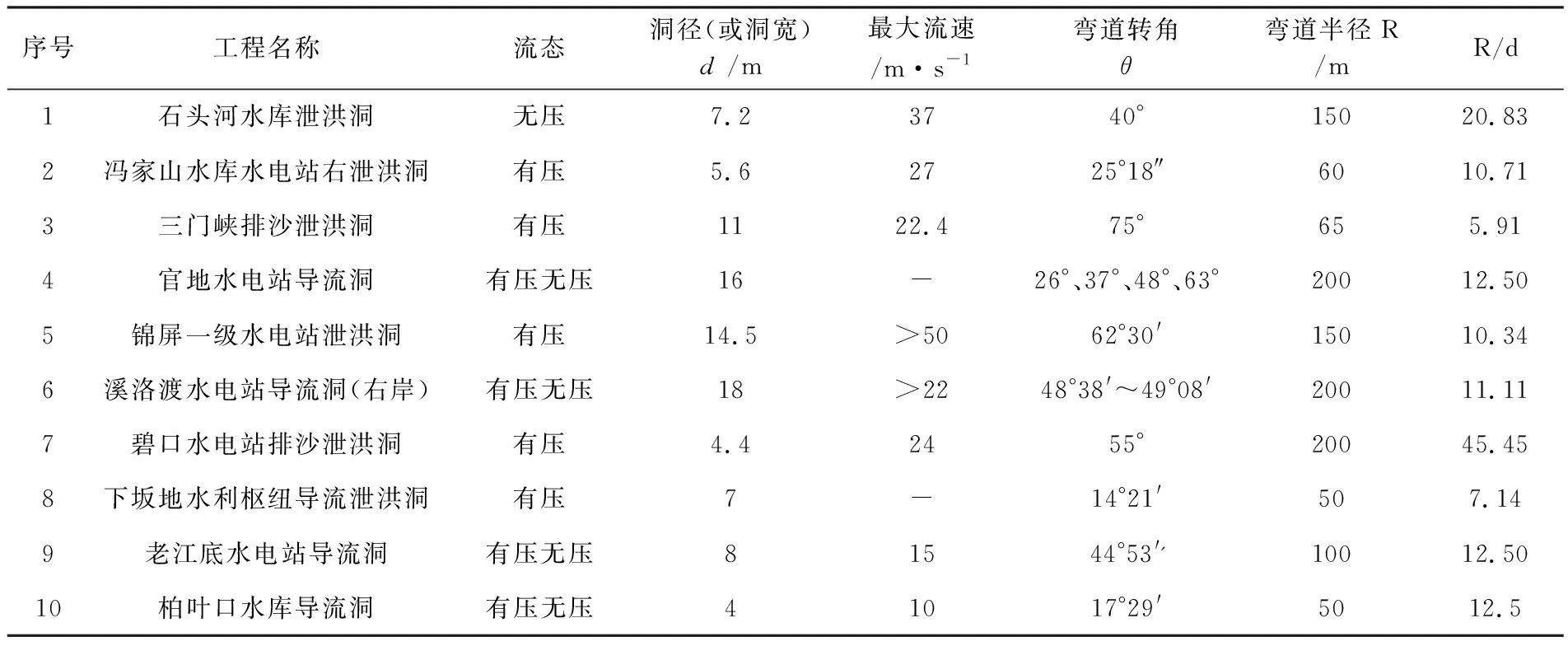
表1 部分隧道工程平面弯道几何特性值

因为弯道的几何特性有两个要素：弯道半径和转角，所以，需要分别控制其中一个要素，另一个要素取不同值，以此研究其规律。然而当这两个要素变化时，弯道的长度会发生变化，如果其他直线段都不变的话，整个导流洞的长度及出口高程会改变，将对弯道水力学特性有较大的影响。因此，需要改变相应直线段的长度，以求导流洞的总长和出口高程不变，从而保证了各弯道方案的边界条件一致。由于工程右岸导流洞弯道后的直线段很短，规范又要求弯道后必须设置直线段，且长度不宜小于5倍洞径(或洞宽)，因此，方案设定中改变弯道前的直线段，不改变弯道后的直线段，从而保证弯道后水流平顺过程的一致性。弯道方案选择如表2所示。

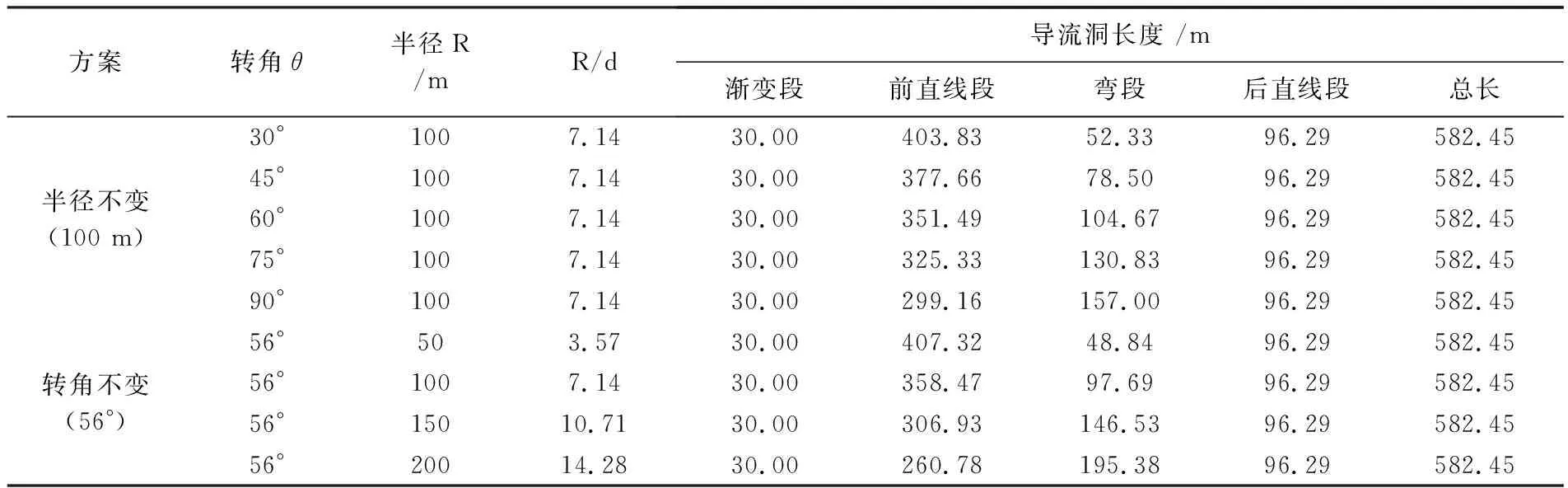
表2 各方案设计参数表

3 数值模拟计算成果分析

3.1 弯道转角对弯道水力学特性的影响

笔者定义压差为某断面沿水流方向弯道外侧与弯道内侧的压力之差。在两侧直墙处沿垂直方向各取40个点，得到40个水平面上的压差，再把40个压差进行平均得到某断面压差。从图1中可以看出，弯道起点和弯道终点的压差基本相同，且都小于弯道中段的压差，弯道水流中最大压差出现在弯道中段。此外，转角越大，弯道水流的压差就越大，但影响幅度较小，转角30°的弯道中段压差为3.92 m，转角90°同样位置的压差为4.18 m，两者相差仅0.26 m。由此可见转角对弯道的压力分布有一定的影响，转角越大压差越大，但影响程度很小。

由图2可以看出，弯道内流速分布明显要比压力分布复杂，转角对流速偏移的影响程度更大一些。首先，偏流系数为负值指的是流速偏向弯道内侧，为正值代表的是流速偏向弯道外侧。不管是在刚进入弯道时水流偏向内侧，还是在导流洞出口处水流偏向外侧，随着转角的增大，流速偏移程度都会增大。也就是说转角越大，水流的偏移幅度越大，水流越不稳定，流态越复杂，特别是当转角大于75°时，偏移幅度明显大于其他角度。因此在设计弯道时，尽量避免大于75°的转角出现。

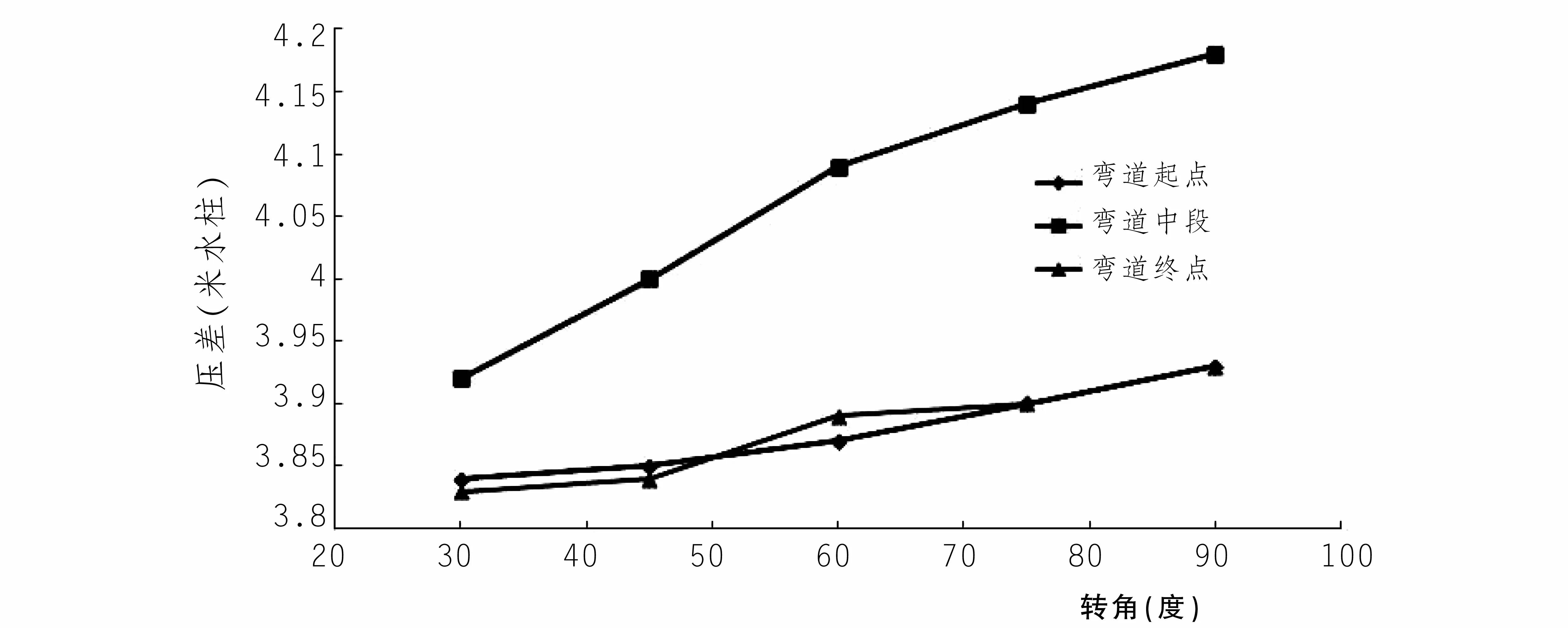
图1 转角对弯道压差的影响

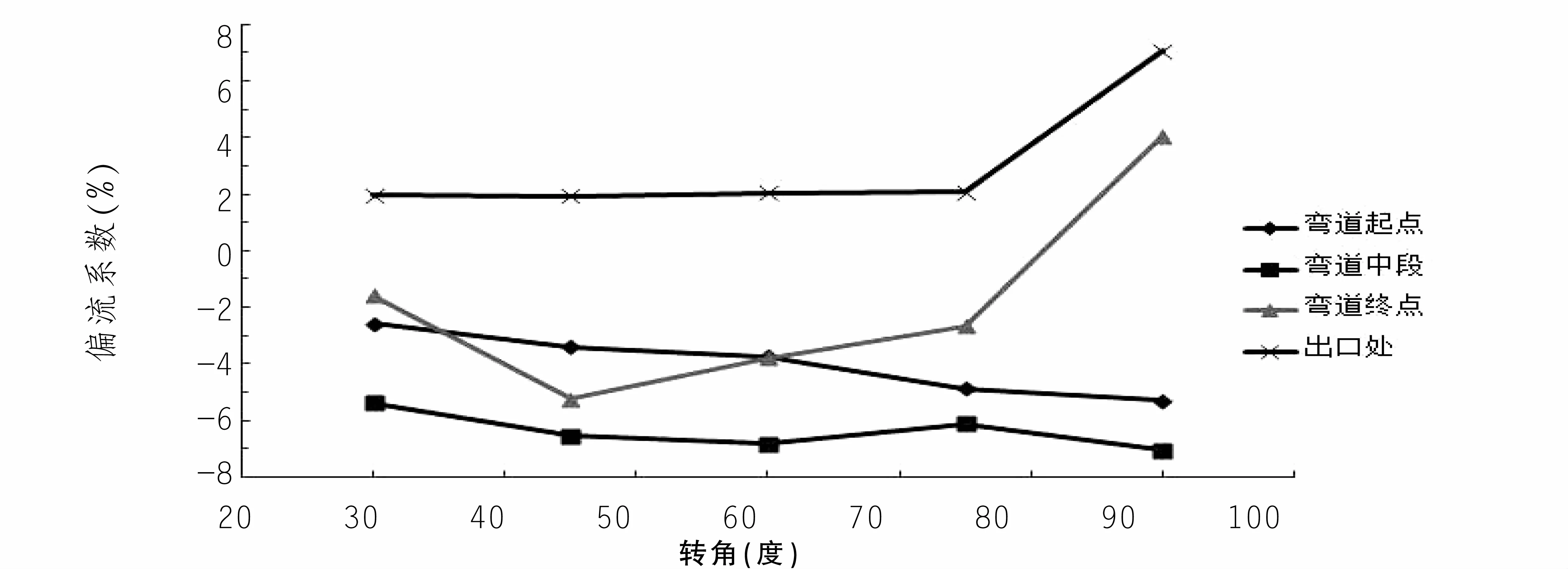
图2 转角对弯道及出口偏流系数的影响

3.2 弯道半径对弯道水力学特性的影响

由表3、图3可以看出，无论半径大小，弯道中的压力分布趋势均是一致的，弯道中段的压差最大，而弯道两端的压差基本相同。随着半径的增大，压差逐渐减小，弯道半径过小会造成非常大的压差。当R/d为3.57时的弯道内外压差最大达到8.04 m，是R/d为14.28时的四倍。但R/d再持续增加时，半径对弯道压差的影响显著变小，增大半径对改善压差的作用不再明显。

由图4可以看出，弯道半径越小，水流的偏离现象越严重。当R/d小于7时，不管偏向弯道内侧还是外侧，偏离程度显著增大，当R/d=3.57时，其偏移幅值接近20%；当R/d大于7时，半径对水流偏离的影响就很小了。

表3 不同半径的弯道压差值

4 结 语

利用经过验证的导流洞三维数学模型，重点研究了弯道水流的压力、流速分布规律以及弯道转角和弯道半径对洞内压强、流速的影响，得出如下结论：

图3 半径对弯道压差的影响

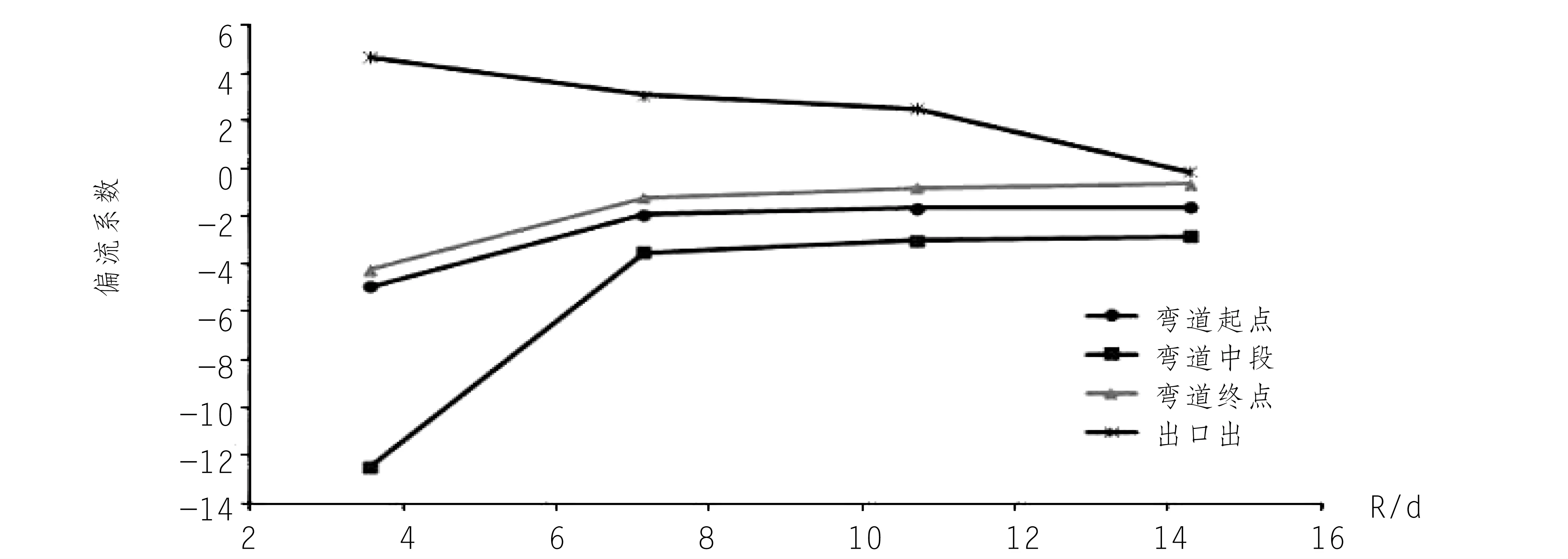
图4 半径对弯道及出口偏流系数的影响

(1)水流经过弯道时，压力会发生偏移，弯道外侧压力大于弯道内侧压力，在弯道中段时两侧压差达到最大。

(2)水流经过弯道时，流速也会发生偏移，与压力不同的是，水流在进入弯道后先偏向内侧，在弯道中段附近达到最大，然后在离心力的作用下，高流速区开始向外侧转移。

(3)在半径不变的情况下，随着转角的增大，弯道内外侧压差也增大，但增幅不大，影响不明显；当转角大于75°时，弯道终点及出口的偏流系数明显增大，偏流现象明显，需进一步加长弯道后直线段长度，以改善水流条件。

(4)在转角不变的情况下，随着半径的增大，弯道两侧压差显著减小，弯道及出口偏流系数也逐渐减小。当R/d在3.5至7之间时，压差和偏流系数变化特别明显。

(5)导流洞弯道水流的压力、流速分布规律及弯道转角和半径对弯道水力学的影响同样适用于其它水工隧洞。