IGBT热网络传热模型研究
陈 明,曾书俐
IGBT热网络传热模型研究
陈 明1,曾书俐2
(1. 海军驻广州四二七厂军事代表室,广州 510715;2. 中船黄埔文冲船舶有限公司,广州 510715)
在加入层间接触热阻的7层Cauer热网络模型基础上,考虑了材料导热系数随温度变化的函数关系,在芯片结构和实验测试结果基础上加入了结表热阻以及各物理层间的扩散热阻,建立了一种改进的多维IGBT热网络传热模型。采用所建模型对模块各物理层温度特性,特别是结温特性进行了仿真计算,并和实际探测结果进行比对分析。分析结果表明改进的热网络模型较传统热网络传热模型具有更高的精度。
绝缘栅双极型晶体管 热网络 传热模型
0 引言
绝缘栅双极型晶体管(IGBT)是一种综合了功率场效应晶体管和双极型功率晶体管结构的复合型功率半导体器件[1],是目前应用最为广泛的全控型电力电子器件[2,3]。IGBT的工作特性受温度的影响很大[4-6]。首先,由于半导体材料的物理、热学以及力学特性随温度发生改变,IGBT的开关速度、通态压降、漏电流等性能参数都将随温度发生变化,同时芯片还受最高工作结温的限制;其次,IGBT模块内的键合引线、焊料层等封装材料长期受到温度波动与热应力的反复冲击将产生疲劳老化[7,8],从而对IGBT的寿命产生影响。因此开展传热特性与传热模型仿真研究,查明IGBT的各层温度与热传递过程,建立精确的传热模型和准确预测温度对于确保IGBT安全运行、延长工作寿命、提高散热和封装设计以及可靠性都具有重要意义。
为达到降维简化处理的目的,传热问题一般采用热电比拟法,该法是根据传热学集总参数法[9-11](LPM)和电路理论来形成等效热路,热网络图中的热源为IGBT芯片所产生的损耗热量,损耗热量通过模块各个物理层由热源向散热器传递,形成一个复杂的传热网络。其中模块芯片和封装各个物理层分别用集中热源和等效热阻来代替。等效热网络法是个经验模型,易于通过试验提取参数,优点在于能够快速计算模块损耗,便于实现实时仿真,适用于对模块封装各物理层的平均温度进行估算[12,13]。
首先对IGBT传热特性进行了实验测试。通过加入层间的接触热阻、考虑材料导热系数随温度变化的函数关系,以及在芯片结构和实验测试结果基础上加入结表热阻,从而建立了改进的IGBT热网络传热模型。然后考虑DBC上铜层以下各层扩散热阻建立了多维等效热网络模型。最后采用所建模型对模块各物理层温度特性特别是结温特性进行了仿真计算,并和实际探测结果进行比对分析。
1 IGBT芯片结构
IGBT芯片分为两层:硅片层和镀层。镀层镀在硅芯片上表面,由金属层和边缘保护层两部分组成。中心区域的金属层镀铝有两个作用:一是为了保护芯片的完整;另外是为了键合处两端的材料尽可能一致,减小键合处的热膨胀率。边缘区域即镀层四周的黑边框为边缘保护层,镀Si3N4,对芯片起绝缘保护、阻断高压的作用。
2 IGBT传热特性实验测试研究
2.1 IGBT动态热阻抗提取
在一定范围之内,IGBT的某些电学特性与芯片温度间存在一一对应关系,如导通小电流条件下IGBT的导通压降V和栅-射极压降V和温度间近似呈线性的关系,电参数法就是基于这一原理来测量IGBT芯片的平均结温。得到IGBT结温后再联合其它方法测得壳温、导通电流、通态压降参数,可计算得到反映IGBT阻止热量传递能力的热阻参数,其单位为℃/W。其中结-壳热阻[14]定义为:
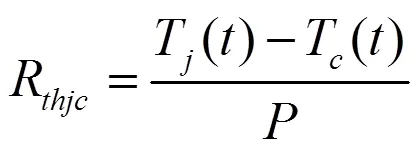
式中T为结温,T为壳温,为耗散功率。由于V测量简便、准确度高,因此采用V作为热敏参数。采用热敏电参数法测量温度首先要进行定标,在恒温烘箱里将测试模块从40 ℃加热到150 ℃,间隔10 ℃记录一次,共得到12个温度点下的V值,标定得到模块温度校正曲线如图1所示。
通过最小二乘法拟合得到结温与V之间的校正公式:
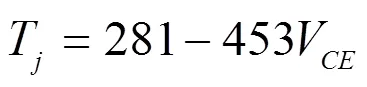
图1 结温定标曲线
完成温度标定后,可进行IGBT结温测量,提取得到反映其传热特性的动态热阻抗曲线。测试时将待测模块固定在散热器上,连续开通恒定的大电流源,在导通电流的同时采用电压表和热传感器测量V和底板壳温。待温度稳定后,由加热大电流源导通状态转换到小电流源导通,由已得到的定标曲线和实际测量得到的V值可计算出该时刻结温,再代入公式(1)计算得到该时刻的瞬时热阻抗值。设定加热电流为50 A,采样小电流为0.1 A,每2 s取样一次。加热过程中提取到的动态热阻抗曲线如图2所示。
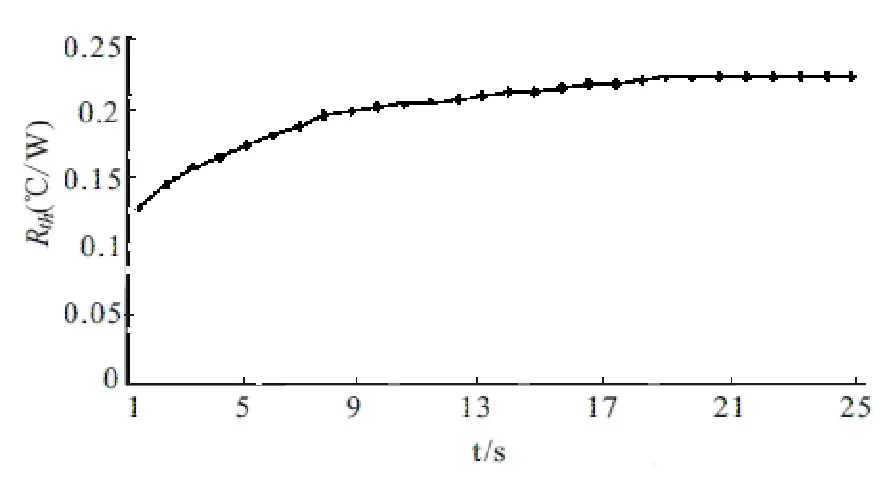
图2 动态热阻抗曲线
由图2中数据可得该型IGBT的结壳稳态热阻为0.23 ℃/W。表1给出了稳态时对应的结温、结壳温差和上升时间。改变加热电流,得到的多组数据如表2所示。
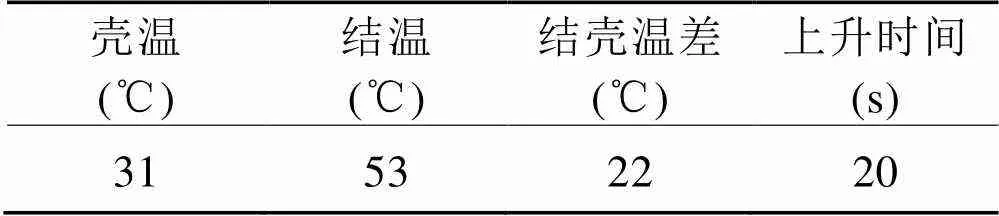
表1 50 A稳态时对应的结温、结壳温差和上升时间
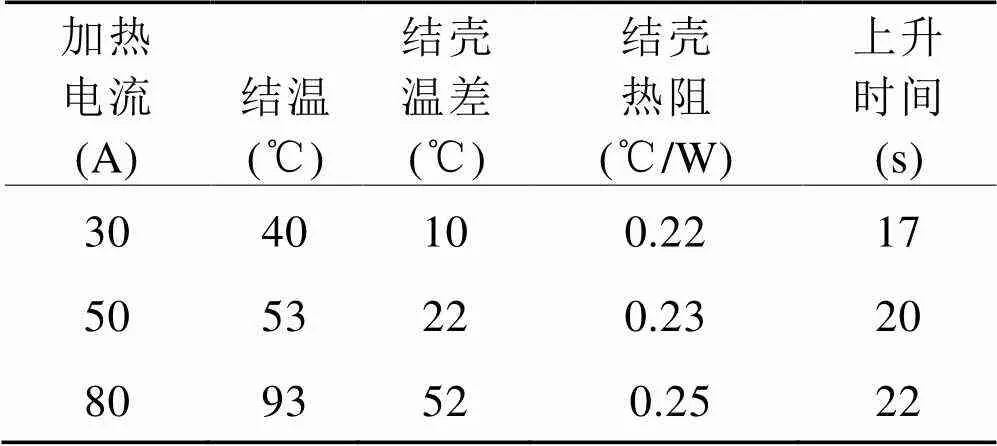
表2 不同加热电流模块热特性参数
从表2中的数据可以看出,结壳稳态热阻随加热电流的增大而略有增大。
2.2 温度分布的红外热成像法探测
一般的商业IGBT模块都是已封装好的、有外壳封装的成品,同时内部芯片表面还覆盖有一层硅胶。为了能够使用红外热探测法对芯片表面实时温度分布进行探测,实验采用了在某生产厂家定做的打开封装且去除硅胶型号为GD50HEL120C1S的1200 V/50 A模块,并搭建了测试平台。
在测试平台中,模块壳温采用高敏度测温热电偶测量,芯片表面温度分布采用高速红外热成像仪直接测量。该高速中波红外热像仪为Xenics公司产品,具有高速连拍功能,可以在1 s内连续拍200幅,可以用来对IGBT的实时工作结温进行探测。
采用已知发射率的绝缘胶带法来校正探测结果。首先在被测金属表面涂一层绝缘漆或是粘贴黑色绝缘胶布,先测量漆或胶布表面温度,由于黑色漆和胶布发射率都接近0.95,同时都很薄且导热性好,与被测金属的温差很小,可认为等于金属表面温度。将测量得到的漆或胶布表面温度与直接测到的金属表面温度代入计算公式[8],计算出被测金属的发射率,输入热像仪成像软件后,就可以直接进行温度测量。当加热电流为50 A时探测结果如图3所示。

图3 粘贴胶布后芯片表面温度分布
图3 中颜色越亮表示温度越高。在芯片表面取A、B、C三点,分别代表中心位置、边缘位置、最边缘位置,对应的温度如表3所示。

表3 芯片表面A、B、C三点温度
由图3和表3中数据可以看出,芯片表面中心温度要高于边缘温度3~4 ℃,从中心区域到边缘区域芯片温度逐渐降低,由中心逐渐向边缘扩散过程比较均匀。这主要是由于芯片中心是键合引线连接处,电流密度最大从而导致热流密度最大。
校正芯片表面材料发射率后,设定加热电流为50 A时,采用已建立的实验系统,测试得到芯片表面不同时刻的温度分布云图。IGBT芯片表面温度上升很快且幅度较大,在20 s左右芯片表面最高温度从接近室温上升到约51 ℃。温度分布云图不同时刻芯片边缘芯片中心点温度如表4所示。改变加热电流,测试得到的结果如表5所示。

表4 不同时刻芯片表面中心和边缘温度

表5 不同加热电流下模块热特性参数
从表2、5可知,红外热成像实时探测法获得的结果要略小于电参数法测得的结果。这主要是由于红外方法测试中采用的IGBT芯片表面镀层未覆盖硅胶,IGBT工作时会向外部空间通过辐射和对流散失一定热量,同时电参数法得到的是芯片内部PN结的平均结温,因此这种工作方式与实际电路中有硅胶覆盖的IGBT工作时存在一定差别,但这种差别不会影响芯片表面结温分布与上升过程。
3 改进的热网络传热模型
3.1 加入接触热阻
为将建立的热网络与实际IGBT模块各层结构相对应,采用了Cauer电路结构来建立传热模型。结合IGBT模块的结构特点与传热特性,根据热电比拟理论[15]建立IGBT模块的热网络等效传热模型,首先作如下假设和等效:
1)IGBT芯片产生的热量主要是垂直向下传递,因此建立的传热模型为7阶热网络,与从芯片到基板间的7层物理结构相对应[14]。
2)加入引起一维垂直方向上各层界面温度降落即增加了热量传导过程中附加传递阻力的接触热阻[9-11]。在手册上查到单位面积接触热阻值,乘以层间面积,再加上基板与热电偶之间导热硅脂的热阻,计算得到模块总的接触热阻约为0.01 ℃/W。



针对型号为GD50HFL120C1S的IGBT模块进行建模,模块各物理层对应的材料热物性以及几何尺寸参数分别如表6和表7所示。根据所列参数,由式(3)、(4)可计算得到如表8所示的该模块在温度为300 K时的Cauer结构热网络传热模型。
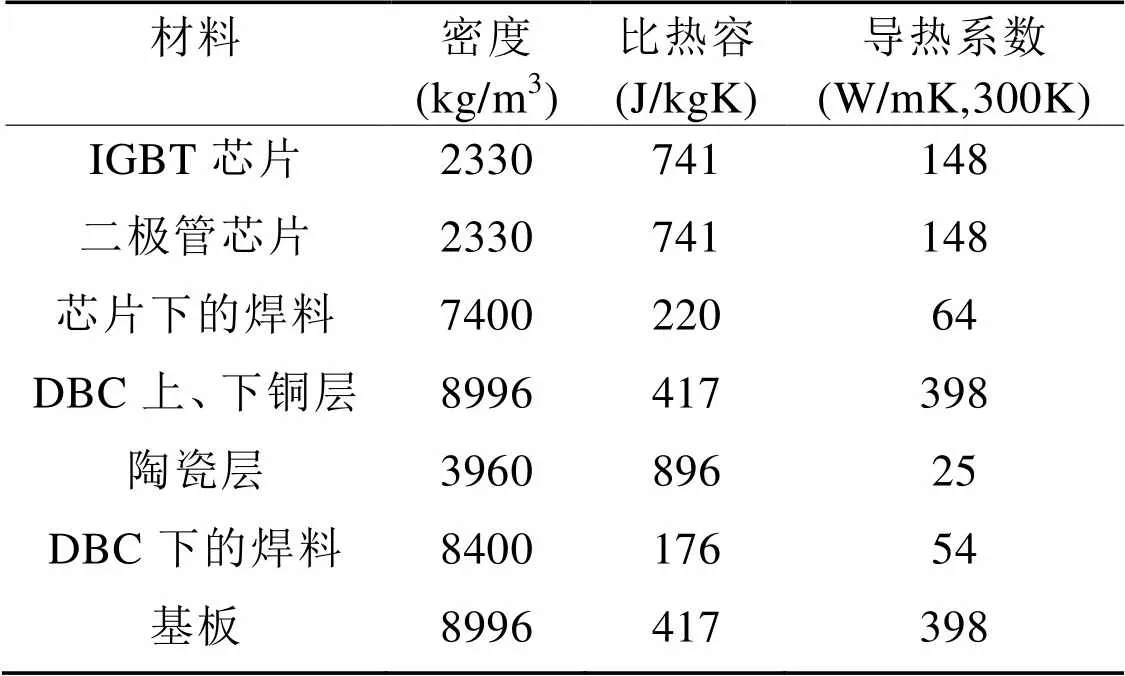
表6 IGBT模块材各物理层材料物性参数
3.2 考虑变导热系数
相关专著[9-11]列出了许多器件所用材料在不同的温度时导热系数。相对硅而言,其它各层材料导热系数随温度的变化很小,如芯片下焊料层在300 K时导热系数为66 W/(mK),在400 K时导热系数为62 W/(mK),因此可以近似为定导热系数。

表7 IGBT模块的各层几何尺寸

表8 各分层等效Cauer热网络结构热阻、热容
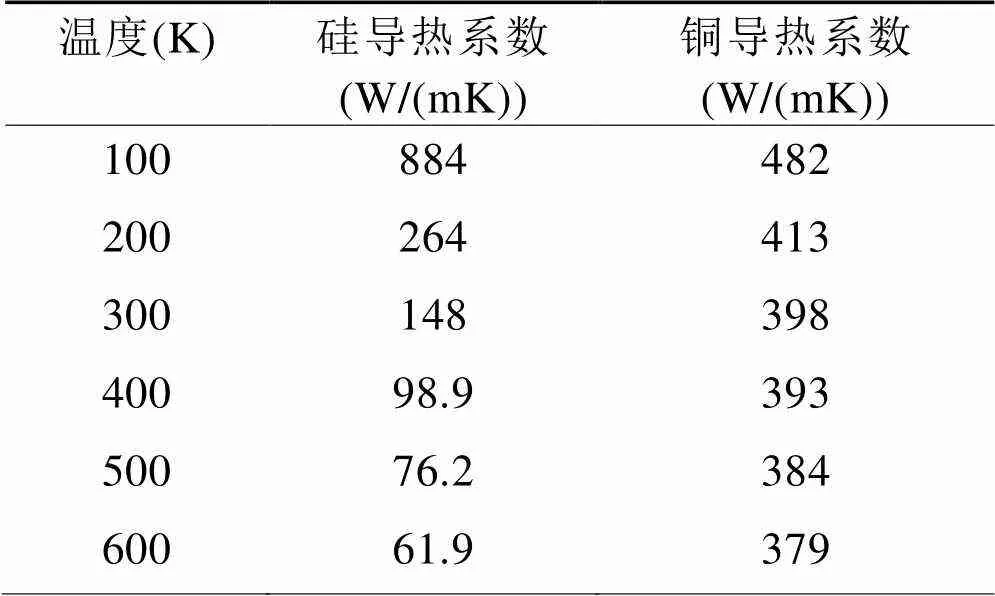
表9 硅、纯铜材料在不同的温度下导热系数

表10 不同温度时对应的结壳材料热阻




因此,式(3)可修正为:
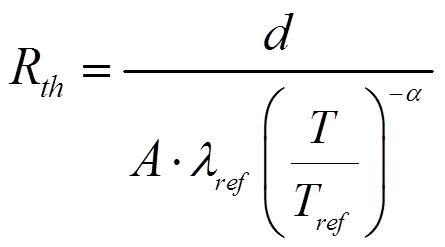
将不同温度时各层材料的导热系数代入计算公式,可得GD50HFL120C1S在不同温度时对应的稳态结壳热阻如表10所示。
3.3 加入结表热阻
由实际探测结果,芯片镀层实际温度T小于芯片内部硅层结温T。由芯片硅层结温和芯片表面金属层温度差对应的结表热阻R。即

式中是芯片表面金属层向外辐射的热流量,T为红外测得的芯片表面中心温度,为物体的发射率,为辐射表面积,代入相应数据,可得:
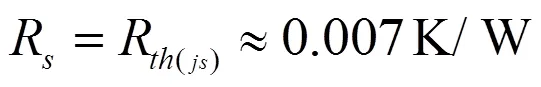
3.4 考虑扩散热阻
芯片焊料层以下各层长度、宽度减去有效传热面积对应长度、宽度后所得的材料热阻即为该层的扩散热阻,于是依据式(3)、(4)计算得到每层扩散热阻后的等效热网络模型如图4所示。需要指出的是,图4中各层的扩散热阻R、R和扩散热容C、C均是对称的,图中只给出一边。图4中对应的物理层扩散热阻值R、R如表11所示。
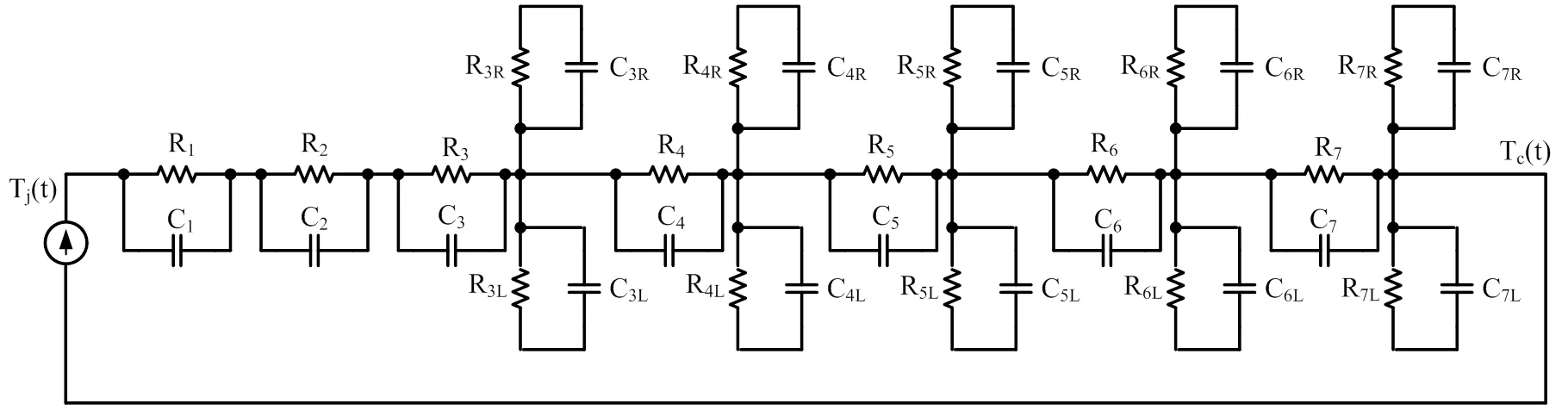
图4 加入扩散热阻热网络传热模型
由表11可知,DBC上铜层以下各层的扩散热阻并不小,这也是导致各层温度存在一个分布的原因。在一些工程应用场合,扩散热阻小的分层温度可用平均温度近似。
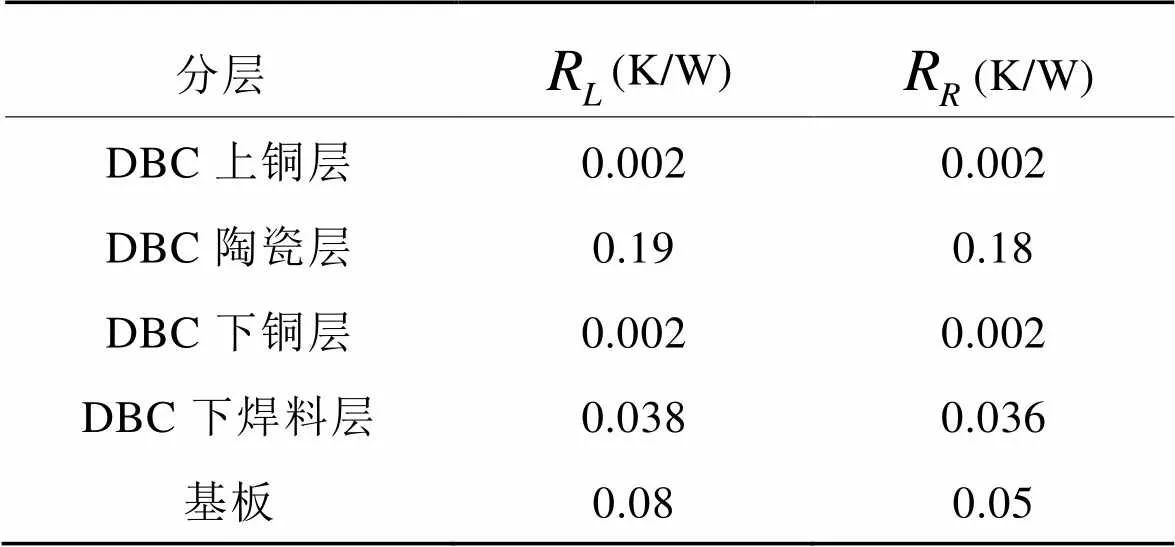
表11 物理层接触热阻
4 仿真研究及模型精度分析
采用建立的RC热网络在Saber仿真环境里搭建了如图4所示的IGBT模块传热模型。在加热电流为30 A、50 A、80 A,壳温设定为稳定时刻温度30 ℃、31 ℃、40 ℃,仿真得到的结温上升曲线如图5所示,其中50 A时各层温度上升曲线如图6所示。
计算得到IGBT传热特性数据如表12所示。从表12中数据可以看出,仿真结果稳态结温以及热阻参数与实验数据吻合较好,而温度上升时间偏小,这主要是由于仿真忽略了散热器的温度上升过程,将最后的稳定温度设定为恒定壳温,因此上升时间比实际过程要短一些。随着加热电流的增大,结壳温差呈加速上升的变化趋势。
当加热电流为50 A时,计算得到DBC上铜层以下各层温度分布,其中陶瓷层和下焊料层如图7所示,温度分布特性数据如表13所示。

图5 IGBT结温仿真上升曲线

图6 加热电流50A时各层温度上升曲线
(a) 陶瓷层温度分布

(b) 下焊料层温度分布
图7 物理层中心、边缘温度上升曲线
从表13中数据可以看出,由于陶瓷层扩散热阻很大,导致该层温度分布不均匀度很大,约为10 ℃,其余各层相对较小。
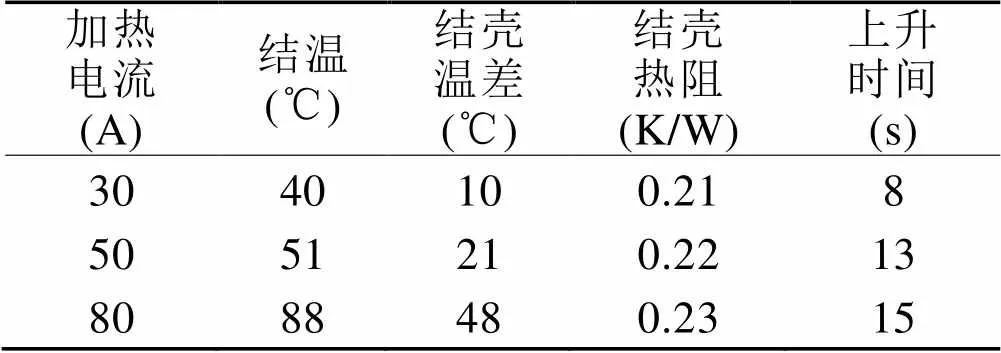
表12 不同加热电流模块传热特性参数
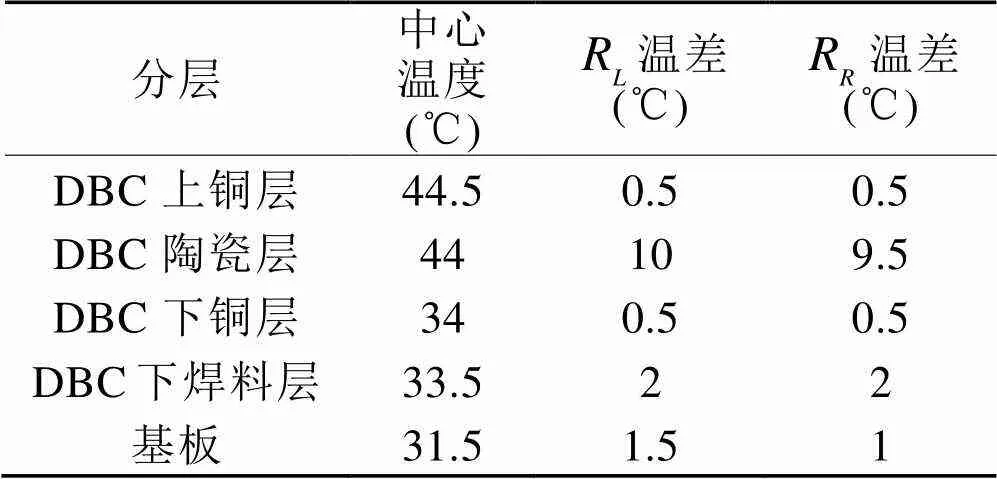
表13 不同加热电流模块温度分布特性
5 结论
1)在加入层间接触热阻的7层Cauer热网络模型基础上,考虑了材料导热系数随温度变化的函数关系,加入结表热阻,以及各物理层间的扩散热阻,建立了一种改进的多维IGBT热网络传热模型,比传统传热模型只考虑定导热系数材料热阻具有更高的精度。
2)总接触热阻为层间接触热阻加上基板与热电偶之间导热硅脂的热阻,约为0.01 ℃/W。结表热阻是通过区分芯片内部结温和表面温度得到,约为0.007 ℃/W。扩散热阻为上铜层以下各层长度、宽度减去有效传热面积对应长度、宽度后所得的材料热阻,由扩散热阻可得温度分布。
3)就所建改进的一维和多维等效热网络传热模型进行了仿真分析,并与实际直接探测和间接测量结果进行了比对分析。分析结果表明改进的热网络传热模型所得到的热阻更接近实验结果,且可实现对各种工作方式下各物理层平均温度波动的精确预测。
[1] 周文定, 亢宝位. 不断发展中的IGBT技术概述[J]. 电力电子技术, 2007, 41(9): 115-118.
[2] 肖华锋, 谢少军. 采用逆阻型IGBT的零电流开关PWM电流源型半桥变换器[J]. 中国电机工程学报, 2007, 27(31): 110-114.
[3] 蔡慧, 赵荣祥, 陈辉明等. 倍频式IGBT高频感应加热电源的研究[J]. 中国电机工程学报, 2006, 26(2): 154-158.
[4] Lefranc G, Licht T, Mitic G. Properties of solders and their fatigue in power modules[J]. Microelectron Reliability, 2002, 42(4): 1641-1646.
[5] Yang S Y, Xiang D W, Bryant A, et al. Condition monitoring for device reliability in power electronic converters: a review[J]. IEEE Transaction on Power Electronic, 2010, 25(11): 2734-2752.
[6] Smet V, Forest F, Huselstein J J, et al. Ageing and failure modes of IGBT modules in high temperature power cycling[J]. IEEE Transactions on industrial ele-
ctronics, 2011, 58(10): 4931-4941.
[7] Bryant A T, Mawby P A, Palmer P R, et al. Exploration of power device reliability using compact device models and fast electro-thermal simulation[J]. IEEE Transactions on industry applications, 2008, 44(3): 894-903.
[8] 陈明, 胡安, 刘宾礼. 绝缘栅双极型晶体管失效机理与寿命预测模型分析[J]. 西安交通大学学报, 2011, 45(10): 65-71.
[9] 陶文铨. 传热学[M]. 西安: 西北工业大学出版社, 2006.
[10] 戴锅生. 传热学(第2版)[M]. 北京: 高等教育出版社, 1999.
[11] Incropera F P等著(葛新石等译).传热和传质基本原理[M]. 北京: 化学工业出版社, 2007.
[12] Ammous A, Ghedira S, Allard B, et al. Choosing a thermal model for electrothermal simulation of power semiconductor devices[J]. IEEE Transaction on Power Electronic, 1999, 14(2): 300-307.
[13] Masana F N. A new approach to dynamic thermalmodelling of semiconductor packages[J]. Microelectronics Reliability, 2001, 41(4): 901-912.
[14] 陈明, 胡安, 唐勇等. 绝缘栅双极型晶体管传热模型建模分析[J]. 高电压技术, 2011, 37(2): 453-459.
[15] Luo Z H. A thermal model for IGBT modules and its implementation in a real time simulator[D]. PhD Thesis, Pittsburgh: University of Pittsburgh, 2002.
[16] Castellazzi A, Ciappa M, Fichtner W, et al. Electro-thermal model of a high-voltage IGBT module for realistic simulation of power converters[C]. IEEE Power Electronics Specialists Conference, Piscataway, NJ, USA: IEEE, 2007: 155-158
Thermal Network Model for IGBT Power Modules
Chen Ming1, Zeng Shuli2
(1. Naval Representatives Office in Guangzhou No. 427 Company, Guangzhou 510715, China; 2. CSSC Huangpu Wenchong Ship Building Co.,Ltd., Guangzhou 510715, China)
TN341
A
1003-4862(2018)09-0001-06
2018-4-19
国家自然科学基金重点项目(50737004)
陈明(1982-),男,工程师。研究方向:船舶电力系统及控制研究。Email: 13715034@qq.com

