蒸发波导模型概述

ESR Jinadasa，田 斌，郭 鹏



蒸发波导模型概述

ESR Jinadasa，田 斌，郭 鹏

（海军工程大学，武汉 430033）

蒸发波导是在海上低空环境中发生概率最高的一种大气波导，可有效利用蒸发波导传播条件使雷达实现远距离目标探测。本文分析了海上大气波导的形成条件，阐述了蒸发波导模型提出的重要意义。综述了几种典型的蒸发波导模型研究应用状况。最后，展望了未来的研究工作方向。

蒸发波导 模型 应用状况

0 引言

大气波导是一种可以使电磁波产生超折射的环境现象，它可以使部分电磁波陷获在波导层内，形成超视距传播，从而增加无线电系统的作用距离，实现超视距探测。蒸发波导是海上发生概率最高的一种大气波导，其成因主要是海水蒸发使得空气中的相对湿度随着高度的增加剧烈下降，从而导致大气折射率垂直分布满足一定的形式所致。该波导具有稳定性较好、持续时间较长，在水平方向上的延伸距离远等特点，垂直高度一般在40 m以内。由于大多数舰载微波雷达的天线架设高度较低，正好位于蒸发波导的有效高度范围内，因此可有效利用蒸发波导传播条件进行远距离目标探测。在海洋上，蒸发波导对雷达等电子装备的影响显著，能准确评估大气环境对敌我双方电子系统的影响，对作战实施人员进行战略部署以及掌握战场制电磁权显得极为重要，鉴于此，各军事强国均在该领域进行了较为深入的研究。低空大气波导对电波传播和探测通信系统等具有重要影响，研究大气波导环境具有重要的现实意义。

1 大气折射基本类型

无线电波在真空中传播的速度约为3×108m/s，传播轨迹为直线，不过在实际媒质中，这两种特性将发生一定的变化，电磁波的速度会减小，当电磁波以一定的角度从传播速度较慢的介质到达传播速度较快的介质交界面时，传播方向将不再保持原来的方向，而是偏向慢速介质一方。

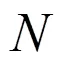
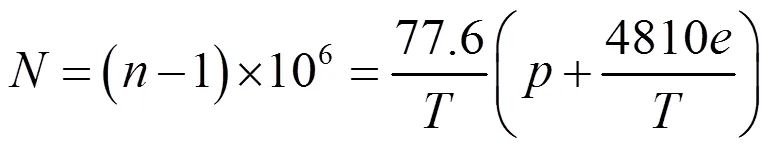
式中，为气压（hPa），为气温（K），为水汽压（hPa）。

将式(1)两边对高度求导得到折射率垂直梯度定义式（式（2）），并按照折射率垂直梯度将大气折射划分为不同类型（表1所示）。

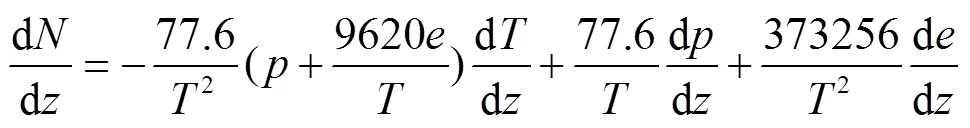
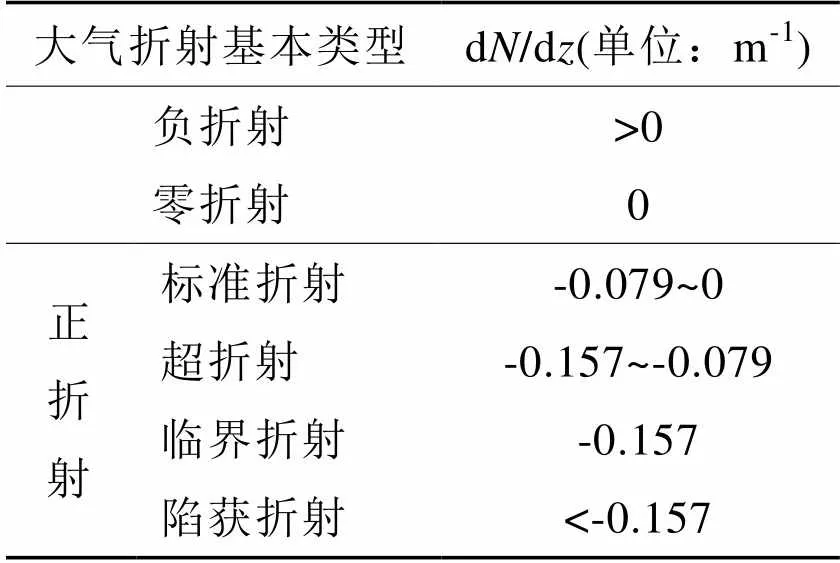
表1 大气折射基本类型及其存在条件

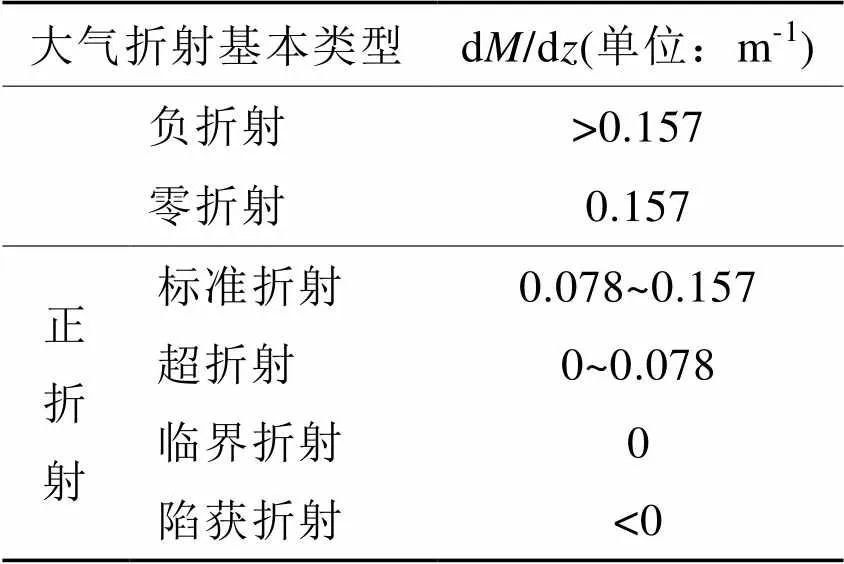
表2 大气折射基本类型及其存在条件

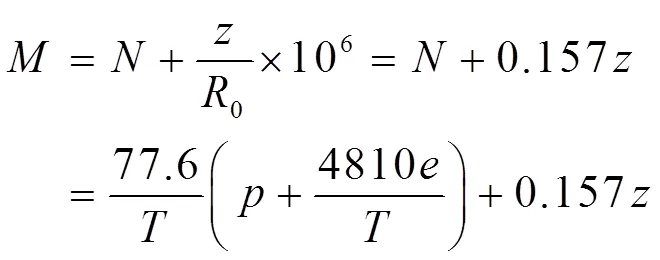
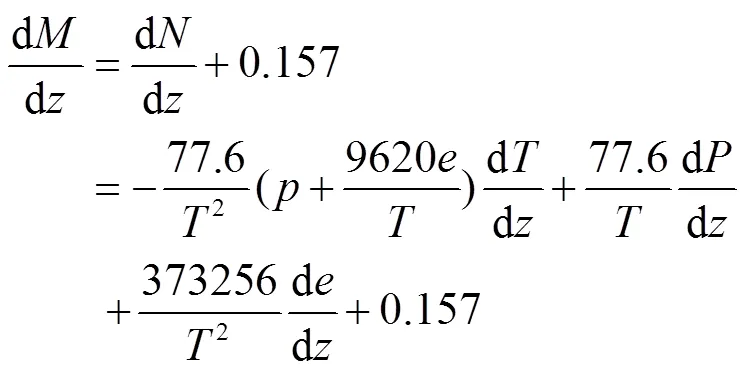
引入修正折射率之后，判别陷获折射产生的条件更加直观，即当修正折射率垂直梯度小于零时，大气折射类型为陷获折射。

2 海上大气波导分类及其形成条件

当大气出现陷获折射时，出现了电磁波绕地球表面的超视距传播现象[1]。此时电磁波的能量被限制在海面与一定高度的空气层之间传播，类似电磁波在波导中传播，因此称这种现象为电磁波的大气波导现象。

对于海洋大气环境来说，有两种自然现象使修正折射率出现负梯度，也就是使电磁波出现超视距传播：一是海水蒸发时出现的电磁波的超视距传播现象，这种由海水蒸发引起的大气波导称作蒸发波导。二是在海面上空，随着高度上升，温度突然升高（逆温）、湿度突然下降，形成的空气层时，出现的超视距传播现象，这种大气波导现象称作表面波导。还有一种悬浮在空中的大气波导称作悬空波导，产生机理与表面波导类似，该类型波导通常出现在3 km（有时甚至达到6 km）的高度以下。

在海洋大气传播的电磁波能否形成大气波导传播，需要满足一定的条件。文献[2]中给出了电磁波形成大气波导传播的两个必要条件：一是电磁波波长必须小于最大陷获波长（或称截止波长）；二是电磁波的发射仰角必须小于某一临界仰角（或称穿透角）。

3 蒸发波导模型综述

3.1 蒸发波导模型的提出

在实际应用中测量大气修正折射率的方法如下：利用专用测量设备如微波折射率仪直接进行折射率、修正折射率的获取；利用探空球搭载传感器进行测量；利用空基、地基GPS观测资料反演大气修正折射率剖面；利用气象学研究的天气预测模式进行修正折射率预报；利用对多地区长期、大量实测数据进行统计得到的折射率经验模型等方法。以上获取大气折射率或修正折射率的方法虽各有优点，但要得到海洋大气近地层中蒸发波导修正折射率廓线，仍显不足，并且以上方法在易用性和保密性等方面都存在一定缺陷。

为了解决传统测量方法易用性、保密性等方面的不足，部分学者在相似理论的基础上提出了蒸发波导模型的概念，只需测量两个高度上的环境参数，即海水表面温度和某个高度处的气温、相对湿度和风速等参数，就可以利用这些模型计算出海上几十米高度以内的修正折射率廓线。蒸发波导高度一般低于40 m，因此用这种方法可以解决海上发生概率最高的蒸发波导修正折射率剖面曲线的测量问题。

目前，全球范围内已知的蒸发波导模型主要有：Jeske模型、Paulus—Jeske模型（简称PJ模型）、伪折射率模型、MGB模型、基于LKB通量算法的模型（包括NPS模型、NRL模型、NWA模型、A模型）、RSHMU模型。上述这些蒸发波导模型都是基于大气近地层相似定理，利用海表温度以及海上某一高度处的气象数据作为输入来得到蒸发波导高度等波导特征量。但上述波导模型在蒸发波导高度的判定准则等方面存在一定的差别，因此得出的蒸发波导高度等特征量结果不尽相同。

3.2 Jeske模型及PJ模型

上世纪六七十年代，德国汉堡大学气象学院Jeske提出了一种蒸发波导模型，被称为Jeske模型，该模型是早期较为成功并被广泛使用的蒸发波导预报模型，之后Jeske模型经多名学者的应用检验，尤其是R.A.Paulus通过对历史资料和较精确的浮标资料的分析，对Jeske模型进行了修正，形成Paulus—Jeske模型，简称PJ模型[3]，现已被美国海军评估电磁波传播的多种业务软件系统所采用，包括较早的EREPS以及最新的AREPS。PJ模型是在Jeske模型的基础上对结果进行一定的修正。

Jeske模型是利用计算出的总体理查森数结果，得出近地层大气的稳定性状况，然后根据不同的稳定性结果，使用与之对应的基于莫宁—奥布霍夫相似定理的函数得出蒸发波导高度结果。

3.3 MGB模型

1992年，Musson-Genon、Gauthier和Bruth联合发表了题为《A simple method to determine evaporation duct height in the sea surface boundary layer》的文章，介绍了一种基于近地层莫宁—奥布霍夫相似理论，利用欧洲中尺度天气预报中心（ECMWF）模式所使用的近地层参数化方案中的有关方法，预报蒸发波导高度的模型，被称之为MGB模型。

该模型利用位温、比湿的特征尺度参数、莫宁—奥布霍夫长度以及位温对应的无量纲化梯度函数来求蒸发波导高度结果，MGB模型采用两种不同的方法来求解上述物理量，一种为解析法，另一种为迭代法。

解析法和迭代法的结果并不完全一致，Luc Musson-Genon[4]等人计算得出，在不稳定层结情况下，两种方法结果偏差不大，但在稳定层结情况下，解析法得到的波导高度结果与迭代法相比，随气海温差增大增加更快。倘若在迭代法中采用Wieringa给出的无量纲化梯度函数，则解析法和迭代法的偏差会变小。所以，Luc Musson-Genon等人推荐使用解析方法确定蒸发波导高度，如果使用迭代方法，应选择Wieringa的无量纲化梯度函数。为了方便起见，将利用解析法求解波导高度的模型称为MGB0模型，利用迭代法求解的称为MGB1模型，利用Wieringa的无量纲化梯度函数的迭代法求解的称为MGB2模型。

由于三种MGB模型均属于第一类蒸发波导模型，因此要想获得模型计算的波导强度，首先需要求出波导模型的修正折射率廓线。目前国内外公开文献中均未给出MGB模型的修正折射率廓线公式，这给求解该模型强度带来了难题。

3.4 RSHMU模型

RSHMU模型是由俄罗斯国立气象水文大学（原圣彼得堡气象水文学院）的A.S.Gavrilov提出的一种波导预测模型，RSHMU即为该大学校名英文的首字母缩写。该模型自上世纪八十年代提出以来，主要在原苏联加盟共和国中使用。近期公开发表的文章中，来自乌克兰国立科技大学无线电物理与电子学院的V.K.Ivanov[5]，V.N.Shalyapin和Yu.V.Levadnyi利用在大西洋和印度洋部分海域的试验数据，将RSHMU模型与其它蒸发波导模型进行了比较，使电磁波波导传播的其他学者逐渐了解了这一模型的特性。该模型首先得到的修正折射率廓线，然后再获取波导高度、强度结果，该蒸发波导模型具体实现方法与基于通量算法的蒸发波导模型相比，区别主要在于风速、位温的无量纲化梯度函数和稳定度修正函数不同。

4 展望

本文对不同的蒸发波导模型进行了综述，但是目前对不同蒸发波导模型在不同海域的适应性问题研究还比较缺乏，因此需要针对具体的蒸发波导模型在不同海域条件下所取得的结果进行对比分析。

[1] Mathew Koll Roxy, Kapoor Ritika, Pascal Terray, Sébastien Masson. The Curious Case of Indian Ocean Warming[J]. Jurnal of Climate, 2014, 27: 8501-8509.

[2] Saji, N. H., B. N. Goswami, P. N. Vinayachandran, and T. Yamagata. A dipole mode in the tropical Indian Ocean[J]. Nature, 1999, 401: 360-363.

[3] Woods, G. S., A. Ruxton, C. Huddlestone-Holmes, etal. High-capacity, long-range, over ocean microwavelink using the evaporation duct[J]. IEEE J. Oceanic Eng., 2009, 34, 323–330.

[4] Anderson, K. D.. 1995: Radar detection of low-altitude targets in a maritime environment[J]. IEEE Trans. Antennas Propag., 1995, 43: 609–613.

[5] Dee, D., and Coauthors. The ERA-interim reanalysis: Configuration and performance of the data assimilation system. Quart[J]. J. Roy. Meteor. Soc., 2011, 137, 553–597.

Overview of Evaporation Duct Models

ESR Jinadasa, Tian Bin, Guo Peng

( Naval University of Engineering, Wuhan430033, China)

O436

A

1003-4862（2018）10-0013-03

2018-05-11

ESR Jinadasa（1979-），男，硕士研究生。研究方向：信息处理与系统。E-mail: 2908320020@qq.com