销/孔定位结构公差设计中的功能边界分析法

徐旭松，吴德辉

（1.江苏理工学院 机械工程学院，江苏 常州 213001；2.博世电动工具（中国）有限公司，浙江 杭州 310052）

1 引言

边界是设计给定的具有理想形状、方向和位置的极限包容面（或被包容面）。边界的尺寸就是该极限包容面（或被包容面）的直径或者宽度[1]。由于边界通常包含了尺寸和几何公差综合作用的结果，因此在精度设计和分析过程中，边界理应“扮演”重要的角色。边界反映的是设计人员的设计意图，在发达国家的先进企业，利用相关要求、边界等来控制尺寸要素的尺寸及几何误差已得到广泛地应用。我国虽然已经在有关标准中引进了相关要求、边界等概念，但多数企业，特别是从事工艺设计的工程技术人员，不能正确理解相关要求和应用边界来进行几何尺寸与公差设计，不能正确实现设计要求，从而或者不能满足功能要求、或者不能获得好的经济效益[2-3]。

一面两孔（销）是机械工程中常见的定位方式，其精度设计对产品功能至关重要。设计人员常常习惯以尺寸公差（正/负公差）为主来控制定位精度，忽视了公差设计的目的是为了保证几何功能性。一些设计实践证明：过去只按零部件尺寸进行定位元件的定位尺寸及公差与配合设计总存在着这样或那样的问题[4-6]。而以几何公差为主来控制几何要素的几何变动，并采用功能边界分析方法进行公差分析和分配能大大提高定位元件设计与制造的一次性成功率，缩短制造周期。

2 实效条件边界-功能边界

为了将公差标准中的不易操作的语义和图示形式的公差带实用化，文献[7-8]从功能要求的角度提出了用于公差描述的实效边界要求（Virtual Boundary Requirements，VBRs）和条件公差（Conditional tolerances，CTs）的概念，用边界的概念代替公差带。当相关要求应用于几何公差规范时，就形成条件公差，此时公差带的边界形成实效条件边界（Virtual condition boundary，VCB）。VBRs要求零件实际要素（提取组成要素）必须位于实效边界之内，给出两种类型的实效边界要求：（1）装配要求；（2）材料体积要求。装配要求是对零件材料增加量的限制；材料体积要求是对零件材料减少量的限制。ASMEY14.5-2009标准将实效边界分为内边界（Inner Boundary，IB）和外边界（Outer Boundary，OB）[9]，对于孔来说，内边界以内永远没有材料，外边界以外永远有材料，而内外边界之间则一定是有材料和没有材料的不确定区域；对于轴来说，则相反。实效条件边界（VCB）是尺寸公差和几何公差共同形成的边界，实际要素（提取组成要素）全部位于装配要求及材料量的实效边界之内则认为满足功能要求，零件合格，因此VCB也可称为功能边界（Functional Boundary）。实效边界反映几何功能要求，其本身就是相对于基准或基准系的一个理想几何要素（或称为特征），它具备几何要素的4大特征（大小、形状、方向、位置）。例如，几何公差规范到尺寸要素（Featureof Size，FOS）上、并使用最大实体要求，这将在尺寸要素的实体外部（非材料边）附近形成一个VCB，即最大实体实效边界（MMVB），实际要素不得跨越MMVB；而当使用最小实体要求时，将在尺寸要素的实体内部（材料边）建立起一个VCB，即最小实体实效边界（LMVB），实际要素不能跨越LMVB[10]。实效条件边界计算，如表1所示。

表1 实效条件边界及计算Tab.1 Virtual Condition Boundary and its Calculation

以常见的孔/轴装配中的最大实体实效边界为例。最大实体实效边界（MMVB）通常应用在间隙装配、保证可装配性的场合，要求内特征（如孔或槽）的最大实体实效边界（HMMVB）大于外特征的（如轴或板）的最大实体实效边界（SMMVB），即：

图1 环套和轴的零件简图及其MMVBFig.1 Diagram of Ring Sleeve，Shaft and their MMVB

环套和轴的零件简图，如图1所示。图1（a）为环套（孔），DMMVB为其垂直度公差和尺寸公差共同作用形成的最大实体实效边界（虚线部分），其形状为理想的圆柱，且垂直于基准A，在该边界以内没有材料。根据表1，该边界的直径大小为：

中轴的dMMVB为轴的垂直度公差和尺寸公差共同作用形成的一个最大实体实效边界（虚线部分），如图1（b）所示。其形状为理想圆柱，且垂直于基准B，该边界为轴能够侵犯的最大空间。根据表1，该边界的直径大小为：

由式（2）、式（3），图 1中孔/轴的最大实体实效边界大小相等，故若环套与轴装配，在保证环套上的基准A面贴合轴上的基准B面的前提下，孔/轴的最大实体实效边界重合，如图2所示。此时，轴的外边界OB等于孔的内边界IB，孔/轴完全能够100%顺利装配，实现互换性。

图2 孔/轴配合及其MMVBFig.2 Hole/Shaft Fit and their MMVB

3 尺寸与公差标注及功能边界分析

一连接板组件的装配示图，如图3所示。连接板置于基座之上，连接板的两个定位孔和基座的两个定位销配合，实现连接板和基座之间的定位，保证圆弧段和另两个通孔分别对齐。

图3 连接板组件Fig.3 Assembly of Connecting Plate and Base

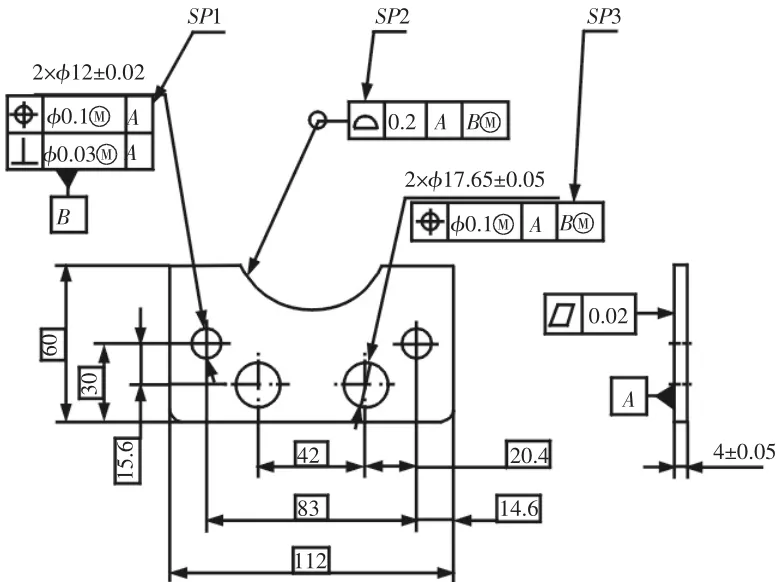
图4 连接板几何规范标注Fig.4 Geometrical Specification of Connecting Plate

连接板的尺寸与公差标注方案，如图4所示。该几何规范采用了多个几何公差项目来控制几何要素变动。图中与基座接触的主平面A为第一基准，它限制了沿z轴平动，绕x/y轴转动；两个φ12±0.02的定位孔与基座上两定位销配合，限制连接板在接触面上沿x/y方向的平动、绕z轴转动3个自由度（存在过约束），故将该两个定位孔（孔组）作为基准B。在A/B基准系中，连接板的6个自由度全部被限制。因而，两个φ17.65±0.05孔用相对于A/B基准系的SP3位置度公差控制，周边轮廓用相对于A/B基准系的SP2轮廓度公差控制。第一基准A采用平面度控制形状误差，第二基准B（两个孔φ12±0.02）一般用第一基准来约束它的几何变动，图样中采用了以A为基准的位置度来控制，并使用最大实体要求。图4中标注SP1位置度的公差带示图，如图5所示。该公差带有如下特点：（1）形状是理想的圆柱，当被测要素处在最大实体状态（MMC）时，圆柱公差带的直径为φ0.1；（2）圆柱公差带的中心轴线与基准A垂直；（3）公差带中心轴线之间的距离为理论正确尺寸83。

图5 SP1位置度公差带示图Fig.5 SP1 Position Tolerance Zone

两个φ12±0.02孔在SP1位置度约束下所对应的最大实体实效边界（MMVB）直径为：DMMVB=DMMC-几何公差=φ11.98-0.1=φ11.88。此时，MMVB=IB。孔组的IB是几何公差和尺寸公差共同作用的一个结果，如图6所示。MMVB以内是一对圆柱形的几何空间，它具备几何要素的4个特征：（1）大小（Size）：它的大小为φ11.88；（2）形状（Form）：它的形状为两个理想的圆柱体（两个圆柱体直径均是φ11.88，圆柱体内永远没有材料）；（3）方向（Orientation）：圆柱的轴线理想地垂直于基准 A；（4）位置（Location）：孔组的两个MMVB作为一个整体垂直于A，其中心轴线之间的距离为理论正确尺寸83。

图6 两定位孔的最大实体实效边界（MMVB）Fig.6 MMVB of Two Locating Holes

两定位孔的“功能边界”明确后，就可用其作为“边界”来设定与其配合的两定位销的边界，进而以实现几何功能为目的来设计基座上主定位销、次定位销上几何要素的尺寸与公差。

4 定位精度分析

定位精度直接影响到产品性能，分析定位精度具有重要的工程意义。一般而言，影响定位精度有以下几个因素：（1）定位特征的尺寸误差；（2）定位特征的几何误差；（3）定位特征在承载工况下的变形；（4）定位特征之间的装配间隙。而定位特征之间的装配间隙是影响定位精度的最主要因素，定位孔和定位销之间的最大装配间隙可认为反映定位精度。所谓最大装配间隙是指当定位孔和定位销均处于最小实体状态时的装配间隙。图3和图4中的两定位孔φ12±0.02的MMVB中心轴线之间的距离均为理论正确尺寸83，计算定位精度时，可将加框格的理论正确尺寸当作“0”误差处理。理论正确尺寸并不是无公差或误差，其真正的公差（公差带）已在相关几何公差中体现和给定，如图4中的SP1位置度、垂直度公差标注及其公差数值，检测评定时也无需评定理论正确尺寸，这也正是采用几何公差进行公差设计和传统的以正/负公差来进行精度设计的不同之处。因此，最大装配间隙（单边）用公式表示为：

式中：Cmax—最大的单边间隙；HLMC—定位孔的LMC时的直径；SLMC—定位销的LMC时的直径。

假设TH、HMMC、HGDT分别为孔的尺寸公差、最大实体尺寸和几何公差；TS、SMMC、SGDT分别为轴的尺寸公差、最大实体尺寸和几何公差；HMMVC为孔的最大实体实效尺寸，SMMVC为轴的最大实体实效尺寸。则有：

而根据表1：

由式（5）、式（6），有：

为了防止装配干涉，且控制最大间隙值来保证定位精度，在设计孔/轴尺寸和几何公差时，通常使孔的内边界IB等于轴的外边界OB，即定位孔的MMVB等于销轴的MMVB：

式中：影响装配定位精度的最大装配间隙的来源由4部分组成：

（1）定位孔的尺寸公差（TH）；（2）定位孔的几何公差（HGDT）；

（3）定位销的尺寸公差（TS）；（4）定位销的几何公差（SGDT）。

若假设基座上定位销尺寸为φ11.88，形状、方向和位置理想，TS=0、SGDT=0、两个定位销轴线之间的距离为理论正确尺寸83，如图7所示。此时，两个定位销的外边界OB=MMVB=φ11.88，与连接板上两定位孔的IB相等，且轴线之间的距离也相等，因而能保证与连接板100%装配成功，如图4所示。

图7 基座定位销尺寸Fig.7 Dimensioning of Pin

根据式（9），最大孔/轴装配（单边）间隙为：

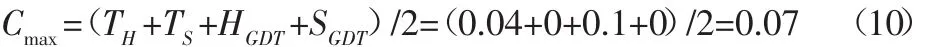
5 改进设计和定位精度分析

以上例子中，若极限为0.07的定位精度不能满足功能要求，或可能给机器的功能带来风险，则需减小最大装配间隙以提高定位精度。一方面，可以通过缩紧定位孔或定位销的尺寸公差和几何公差来达到目的，但这将导致制造成本增加；另一方面，可以改进结构和定位方式，将连接板上的一个定位孔由圆孔改为“长腰”孔，基座两定位销子不变，如图8所示。

图8改进后的连接板组件Fig.8 Improved Structure of Connecting Plate and Base

图8 和图3不同之处在于连接板在基座上沿xy轴平动的自由度主要由主定位销（配圆柱孔）来限制，而连接板在基座上绕z轴转动由次定位销（配“长腰”孔）来约束。因此，在图9的几何规范中，将主接触面A定义为第一基准，主定位孔定义为第二基准B，“长腰”孔定义为第三基准C。比较图9和图4，主定位孔（B基准）只需用SP1垂直度控制；次定位孔（C基准）采用相对于基准A的垂直度和相对于基准A/B的位置度控制（SP4）；用相对于A/B/C基准系的SP2轮廓度和SP3位置度控制另两个几何要素。

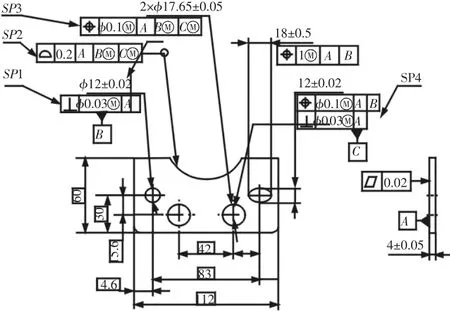
图9 改进后的连接板几何规范标注Fig.9 Geometrical Specification of Improved Connecting Plate

“长腰”孔作为第三基准，主要限制零件绕第二基准B旋转的自由度。因为“长腰”孔已覆盖了主定位销和次定位销在x方向的距离偏差，要使得次定位销能够顺利地装配入“长腰”孔，只需用相对基准A的SP4垂直度公差控制即可。图9中的SP4位置度公差规范主要是为了保证基准系的稳定性以及测量的可重复性，不影响定位精度。

由主定位孔的垂直度几何规范SP1可计算被测要素相对于A基准的最大实体实效尺寸DMMVB=DMMC-垂直度公差=φ11.98-0.03=φ11.95；由次定位孔的SP4垂直度几何规范可计算被测要素对于A基准的最大实体实效尺寸为：DMMVB=DMMC-垂直度公差=φ11.98-0.03=φ11.95。综合主定位孔（B基准）和次定位孔（C基准）的几何规范，在垂直于A基准的方向上总有一对直径为φ11.95的圆柱形的最大实体实效边界，在它以内永远没有材料。同样，若假定两定位销尺寸为φ11.95，形状理想、方向垂直于A基准，两个定位销轴线之间的距离是理论正确尺寸83，如图10所示。此时，两个定位销的OB=MMVB=φ11.95，与连接板上两定位孔的IB相等，如图9所示,且轴线之间的距离也为83，因而能保证100%装配成功。参考式（10）可计算影响装配定位精度的最大装配间隙（单边）：

图10 更新后的基座定位销尺寸Fig.10 Dimensioning of Updated Location Pin of Base

主定位销/孔：

次定位销/孔：

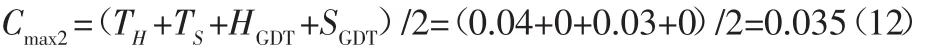
比较式（11）、式（12）和式（10），定位结构改进设计后的定位精度由0.07提高到0.035。再比较图4中SP1和图9中SP1、SP4，可发现改进设计后的定位精度之所以提高是因为利用“长腰”孔避开了对主定位孔位置度公差要求，且两个定位孔之间的距离偏差可以忽略。而连接板具有壁厚薄的特点，其垂直度公差要求相对位置度公差要求更容易保证。

此例中，一面两孔（销）定位结构设计采用圆柱孔-“长腰”孔（或菱形销）比圆柱孔-圆柱孔要容易保证定位精度。但当定位孔/销承受较大载荷时，因载荷而引起的变形成为影响定位精度的主要因素，此时圆柱孔-圆柱孔的定位结构比圆柱孔-“长腰”孔的定位结构更具有优点。例如，在钣金件冲压模具（即便基座是冲压模具的下模）设计中，若采用一面加圆柱孔-“长腰”孔的定位结构，连接板在冲压的过程中，在某个方向上只有主定位孔承受载荷；而采用圆柱孔-圆柱孔的定位结构却有两个定位孔同时承受载荷。

6 结语

功能边界是尺寸公差和几何公差共同作用的结果，它应与设计意图匹配，在设计过程中只有正确分析和利用功能边界，才能在合理保证零件的功能前提下放松公差要求。需要特别指出的是：精度设计并不应是传统的结构设计完成后的工作，而应与结构设计同步展开，结构的改进常能实现在不加严公差要求地情况下提高定位、运动精度，在实际工程应用中，应该根据实际的工况灵活运用。